培养高中生数学解题技巧的教学研究
☉江苏省盱眙中学 于后勇
在学习过程中,数学老师应该了解班级中每个学生具体的学习能力,然后根据他们能力的强弱制订相对应的学习方案.但是,教师们通常提倡的学习理念与学习方法还是比较单一的,课堂比较乏味,氛围不够理想,导致学生在学习的过程中没有足够的学习兴趣.而解题能力是测试学生学习能力的一个重要环节,解题水平的高低对学习成效有直接的影响.通常情况下,班级内会有相当一部分学生的解题能力不稳定,对学习活动的正常开展造成一定的阻力,因此,加强对高中数学解题技巧的学习研究非常重要,这对学生的学习成效有很大帮助.
一、多角度审视
教师应从多个角度合理地培养学生的解题能力,无论是数学公式还是几何图形,都比较复杂,因此怎样可以有效地解题,就需要针对性地审题观察,准确找到解题的切入点.因此,从多种角度进行观察分析,可以帮助我们找到问题的切入点,因材施教,让学生找到适合自己的解题思路.如下文中三角函数例题就可以从多角度去审视题目,并运用不同的基础知识进行解题.
例1若,则函数y=tan2xtan3x 的最大值为______.
解析:此题中tan3x 没有相应的公式对应,因此可以运用换元法将其中的tan3x替换掉,从而可以让学生独立思考如何替换,在这一环节中学生可以审视出两种换元方法,即t=tanx 或是t=tan2x,然后再进行不同思路的思考.
方法1:(运用二次函数求最值)令tanx=t,

方法2:(运用均值定理)令tan2x=t,

由此可见,观察能力在数学解题中是一项基本能力,它可以帮助学生将所看到的考试题目转化成他们平时所学习的具体数学内容,尽可能地从多个角度展开观察与分析,有助于把握题目的整体性,这样可以有效提升解题效率.
因此,解题时我们不能因为小技巧能够解开题目而忽视了对题目整体性的分析,通过这个机会一步一步地培养学生的观察能力,然后老师应根据学生的实际情况,慢慢去引导学生对自己的解题思路进一步完善,一步步地提升学生的解题能力.总的来说,从多角度、多层次审视题目不仅可以培养学生的观察能力,还可以活跃他们的解题思路,为他们以后的学习活动打下基础.
二、多层次分析
多角度审题可以帮助我们找到问题的切入点,除此之外,多层次的分析也必不可少.在进行解题时,学生除了进行多样化、全面化的审题,还需要根据题目进行合理的筛选,这样才可以最高效率地找到正确的解题途径,然后才能进行下一步更高层次地运用解题方法.数学知识往往是非常复杂、非常抽象的,因此,对学生的解题能力的培养是一件长期的任务,只有进行多层次的解答,才能帮助我们透过现象看透题目真正的考核意图.
例2已知圆O 的半径为1,PA、PB 为该圆的两条切线,A、B为两切点,那么的最小值为______.
解析:针对此题,大部分学生会选择应用诱导公式来进行求解.
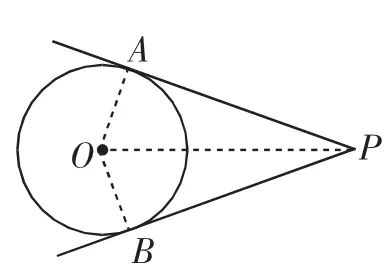
图1

但若是将其转换成二次函数,思路将会更加清晰而且更易理解此题的本质.

在实际的数学学习过程中,教师应积极主动地参与进去,具体深入地去了解学生掌握的情况,找到其中还存在的问题,以正确答案为基础,让学生掌握更加清晰的解题步骤,促使学生在解题中可以仔细观察和分析,提高他们的解题效率.
在解题过程中,如果能够多层次去观察和分析,就会提高解题能力,通过不断的预测和观察,一层层找到其解题方法和捷径.拥有丰富的观察力和灵活的思维能力,更容易快速找到其解题策略.
三、类比和归纳
面对复杂、抽象的数学知识点,如何发现其规律,使之变得简单而具体,就需要我们有着较强的观察力和多层次的数学观察理念,从而有针对性地解答数学问题.培养学生的积极性与主观能动性,在他们的头脑思维中一步步地形成多角度解题模式,类比是不可缺少的.类比解题思路是一种非常明确的解题思路,就是运用学生平时学习的知识点,从多个角度、多个层面展开观察,并将所捕捉到的知识重新加以比较分析,从而更深入地掌握数学解题技巧和规律.如遇到数列相关问题,有时应用基础的等差(比)的通项公式或求和公式推断不出来,此时类比及归纳法是最直接有效的解题思路.
例3等比数列{an}的前n 项和为Sn,已知对任意的n∈N*,点(n,Sn)均在函数y=bx+r(b>0 且b≠1,b,r 均为常数)的图像上.当b=2 时,记bn=2(log2an+1),n∈N*.
证明:对任意的n∈N*,不等式·成立.
证明:分析可知r=-1,当b=2 时,an=2n-1.
因此bn=2n(n∈N*).

所以当n=k+1 时,不等式也成立.
根据(1)和(2)可知,对任意的n∈N*,不等式都成立.
因此,在实际解题过程中,不断发现其规律,找到其内在相似之处,推测出另一种特性,展开想象的翅膀,进行推测、猜想、分析,最后得到一种结果,并且进行检验,这种解题思路也是值得不断探索和付诸于现实的.
四、枚举法
当学生遇到无计可施的情况时,还可以采用枚举法.这种解题方法不同于类比和猜想,而是在别的解题方法行不通的情况下,就可以采用枚举法.一个问题中可能会有各种各样的答案,且不可能应用到具体的解题规律进行筛选,确定最终答案,那么我们就可以通过检验答案进行解题,如果检验问题的答案是正确的,则是适合此题的答案,不过,检验也比较烦琐,操作量也比较大,但是,解题效果还行.当然,在此过程中,切不可出现遗漏,以免失分.
五、结论
总之,教育事业,不仅是单纯地传授理论知识,还应该培养学生的学习能力,教给学生灵活的解题技巧和方法,面对实际问题,能够开拓思维、灵活应对,提高实践操作能力.特别是在数学解题中,要多角度、多层次地不断分析,探索事物的内在规律,选择与之相适应的解题方法,运用类比、猜想、枚举法等,不断提高解题效率.

