基底建系是通法，向量策略“三板斧”——2019年江苏卷第12题

☉江苏省宜兴市第二高级中学 吴勇珍

平面向量问题一直是江苏高考、模拟考填空题后四个小题中的常客，难度中等，方式新颖，背景创新，一直备受关注.破解平面向量的一些常用方法与常见技巧一定要深入理解与熟练掌握，其中基底法是破解的重点，需要通过平面向量的线性关系的转化来厘清；而涉及直角或相关问题时考虑通过建系法，利用平面直角坐标系中的坐标运算来处理；而在一般问题中，经常借助特殊图形加以一般性来解决，又极化恒等式法是一个出现频率较高的基本方法，采用这两种方法，往往可以达到省时省力、提高解题效益的目的.

一、真题在线

【高考真题】（2019 年江苏卷12）如图1，在△ABC中，D 是BC 的中点，E 在边AB 上，BE=2EA，AD与CE交于点O.若，则的值是______.

图1

本题以三角形为问题背景，利用中点、定比分点来设置条件，结合平面向量的数量积的关系式来确定位置关系，进而求解在此条件下三角形的两边长之比.破解此类问题，基底法、建系法、几何法是最常见的“三招”，具体破解与切入方式又有不同的形式.

二、多法破解

思维角度1.基底法

基底法是平面向量的本质所在，是平面向量“几何”化的重要特征.通过选用合适的基底，借助平面向量的线性运算把相关的平面向量用这组基底加以表示，进一步结合平面向量的线性运算、数量积等方式加以转化与应用，从而达到求解的目的.

方法1：（基底法1）如图2，过点D 作DF∥CE 交AB于点F，由于D 是BC 的中点，所以F 为BE 的中点.

图2

图3

方法2：（基底法2）如图3，过点E 作EF∥BC 交AD于点F，根据平面几何知识可知，则知AD=3AF，OD=3FO.

方法3：（梅涅劳斯定理法）由条件可知直线EC 分别交△ABD三边所在的直线AB、BD、DA于点E、C、O.

思维角度2.建系法

建系法是将平面向量进行“代数”化的一大特征，是基于可以建系的前提下来进行的代数化处理几何问题.通过建系，把平面向量问题转化为平面向量的坐标运算问题、平面解析几何问题等来处理，往往可以简化推理步骤、优化运算过程、提高解题效益.同时注意，不同的建系法会导致不同的效果，经常可以采用不同的方式来处理.

方法4：（坐标法）以点D 为坐标原点，BC 所在的直线为x 轴建立平面直角坐标系，如图4 所示.

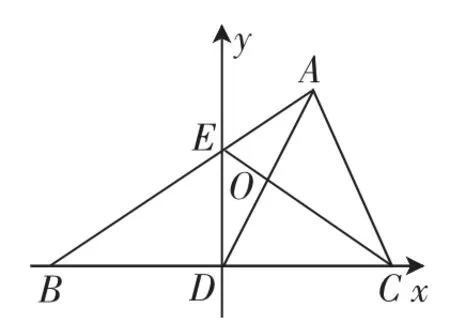
图4

不失一般性，设B（-1，0），C（1，0），A（m，km）（k≠0），由于BE=2EA，结合定比分点公式可得

而AB2=（m+1）2+（km）2=k2m2+m2+2m+1=4m-1+2m+1=6m，AC2=（m-1）2+（km）2=k2m2+m2-2m+1=4m-1-2m+1=2m，可得AB2=3AC2，即

思维角度3.特殊图形法

在一些具有定值结论的平面向量问题，特殊图形法是解决问题比较常见的一种技巧方法.其往往在题目一般性平面几何图形的基础上加以特殊化（如一般的三角形进行特殊化为直角三角形、等腰三角形等，一般的四边形进行特殊化为平行四边形、矩形等），这样处理可以使得问题更加特殊、简单，使解题更直观、更简捷，便于判断与操作.

方法5：（相似三角形法）不失一般性，取△ABC 为以角A 为直角的直角三角形，则有=0.

由于D 是BC 的中点，根据直角三角形的性质知∠B=∠BAD.

三、解后反思

解决平面向量问题，首先就是建立问题中相关几何元素与平面向量之间的联系，通过平面向量的运算，研究几何元素之间的关系.而采用平面向量的线性运算或坐标运算，就是从“形”的思维角度与“数”的思维角度切入，这也是平面向量独具一格的特征.因而，破解平面向量问题时，可以从“形”的角度出发，通过基底法或特殊图形法以“形”的形式来破解；也可以从“数”的角度出发，通过建系法或三角函数法以“数”的形式来破解.不同破解角度，各有各的好，各有各的妙.