基于可能度的区间型指标基坑支护方案优选

王望珍，任美玲,易 琪，邹美伦

(1.武汉大学 土木建筑工程学院，湖北 武汉 430072；2.中科院武汉岩土力学研究所，湖北 武汉 430071；3.深圳市华地岩土工程有限公司，广东 深圳 518110)

随着城市建设的发展，高层建筑越来越多，深基坑也更加频繁地出现在地下基础的建设中。在实际工程中对多个支护方案进行评价和比较，做出最优的选择将大大减小基坑开挖的风险，而且可以节约成本，缩短工期，保护环境。因此，对于基坑支护方案选择的研究至关重要。

在支护方案优选模型方面，张尚根等[1]在模糊数学理论的基础上构造目标函数，建立了综合评价模糊优化模型；蒋崇春等[2]利用模糊物元法及组合赋权法，建立了一种模糊优化理论模型，对深基坑支护方案的优劣程度进行评价；阮永芬等[3]根据灰色关联分析原理构建了基坑支护方案的灰色优化理论模型；王望珍等[4]在传统灰关联理论的基础上，建立了灰色欧几里德关联度优选模型；何满潮等[5]利用人工神经网络理论对支护方案进行优选；冯庆高等[6]运用灰色系统理论和模糊数学理论，建立了基坑支护方案的灰色模糊可变决策模型；高文华等[7]综合运用模糊数学理论和神经网络理论，建立了模糊BP神经网络优选模型。

基坑支护方案优选的问题属于多属性决策问题，其中多数指标为定性指标，存在较大的不确定性，决策者对于问题的判断难以给出准确值，而是倾向于给出一个大概的区间值，因此方案的比较并不是点判断而是区间判断。大多研究是以准确值计算各决策方案的综合评价值，而对以区间数表示的方案评价值的排序研究较少。因此，笔者引入区间数理论，采用区间层次分析法和区间信息熵确定主客观权重，在线性组合规划的基础上确定组合权向量，并利用一种基于可能度的区间数排序方法建立优选模型。

1 基坑优选的综合评价体系

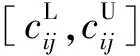
对于定性指标，因其具有极强的不确定性，因此采用区间数表示属性值具有更大的优势。邀请s位专家对所有定性指标进行百分制评分，为方便计算，将百分制评分转化为[0，1]区间上的评分并取平均值作为指标的属性值。

图1 综合评价体系

2 指标权重向量的确定

目前，确定指标权重的方法有主观法、客观法和组合赋权法。组合赋权法综合了主观法和客观法的特点，既避免了主观随意性，又保证了决策者对属性的偏好。因此，笔者采用区间层次分析法确定主观权重ω1，熵权法确定客观权重ω2，并采用基于线性组合规划的一种多属性组合赋权的方法确定综合权重ω。

2.1 区间层次分析法确定主观权重

目前对于层次分析法的实际运用大多是用定值进行决策分析，其结果会存在一定的偏差。因此采用区间数来判断指标的重要程度，使用一种区间层次分析的方法[8]。

2.1.1 构建两两比较的区间判断矩阵

AHP法的关键在于用一定的标度来客观表达人的主观判断。笔者采用SAATY等[9-10]提出的1～9比例标度，对区间数重要程度取值进行两两比较，构造区间判断矩阵。

A=(ai′j′)n′×n′=

(1)

2.1.2 求解区间数权向量

对于给定的区间判断矩阵A=[A-,A+]，区间特征根法的具体计算步骤为：

(1)求A-、A+的最大特征值所对应的具有正分量的归一化特征向量x-、x+。

(2)由A-、A+计算M、N值。

(2)

(3)计算权重向量。

W=[Mx-,Nx+]=(W1,W2,…,Wn′)T

(3)

2.1.3 计算层次总排序

层次总排序是在计算了各级相对于上一级要素的权重向量的前提下，按照从上至下的原则逐层进行迭乘计算，得到各级要素关于系统的总体权重，最后结果即为该评价体系的主观权重ω1。

2.2 熵权法确定客观权重

2.2.1 建立区间数决策矩阵及规范化处理

基于已确定的指标属性值，构建区间数决策矩阵：

C=(cij)m×n=

(4)

式中：i=1，2，…，m,表示第i个评价指标;j=1，2，…，n,表示第j个基坑支护方案。

各类指标可以分为效益型指标和成本型指标两类。效益型指标为数值越大越好的指标，成本型指标为数值越小越好的指标，两类指标的规范化处理方法分别如式(5)和式(6)所示。

若cij为效益型指标,则：

(5)

若cij为成本型指标，则：

(6)

2.2.2 计算熵值

计算第i项指标下第j个方案占该指标的比重：

(7)

对于区间数而言，计算指标输出的熵值应先分别计算区间上下界所对应的熵值，然后取两者的平均值作为该指标的信息熵。

(8)

(9)

2.2.3 计算熵权系数

各指标的熵权系数为：

(10)

则客观权重向量ω2=(ρ1,ρ2,…，ρm)。

2.3 基于线性组合规划的组合赋权

欲使组合赋权的权重向量得到的决策结果与主观、客观赋权下的决策结果尽可能地接近，需使综合权重与各个基础权重决策结果的总偏差最小，故引入偏差函数：

fpij=|rijwi-rijupi|，gp′ij=|rijwi-rijvp′i|

(11)

式中：wi表示各指标综合权重值；up=(up1,up2,…,upm)表示l种主观赋权法确定的权重向量，p=1，2，…,l；vp′=(vp′1,vp′2,…,vp′m)表示q种客观赋权法确定的权重向量，p′=1，2，…,q。

则构建目标函数：

(12)

式中：λp(p=1,2，…,l)和λp′(p′=1,2,…,q)分别为l种主观赋权法和q种客观赋权法的权系数。

(13)

利用该模型进行组合赋权，即可得到属性的综合权重向量ω=(ω1,ω2,…,ωm)。

3 基于可能度的评价模型的建立

已知属性的综合权重向量ω=(ω1,ω2,…,ωm)，按照式(14)可求得方案j的综合属性值。

(14)

显然，得出的综合属性值zj仍是一个区间数，区间数与精确数不同，不便于直接进行排序，目前普遍采用的区间数排序法是一种基于可能度的排序方法。

3.1 建立可能度互补矩阵

按照张全等[11]提出的可能度定义，设a=[aL,aU]和b=[bL,bU]，记L(a)=aU-aL,L(b)=bU-bL，则a≥b的可能度为：

p(a≥b)=

(15)

利用式(15)计算综合区间数zj的可能度，并建立可能度互补矩阵P=(pjj*)n×n。其中，pjj*=p(zj≥zj*)表示zj大于等于zj*的可能度大小，j=1,2,…,n,j*=1,2,…,n。

3.2 计算排序向量

按照樊治平等[12]的可能度矩阵排序公式(式(16))对n个综合区间数进行排序。

(16)

通过计算结果可以得到最终的排序向量为K=(k1,k2,…,kn)，按照kj的大小排序即可得到方案的排序结果，从而判断出最优方案。kj越大，方案越优。

4 实际工程应用及灵敏性分析

4.1 工程概况

该工程为长沙市弘德B6南项目基坑支护工程，地处湖南省长沙市岳麓区银盆岭社区银盆南路与银盆路交叉口。拟建项目由公寓塔楼(26F)、商业裙楼(3F)和地下室(2F)组成。基坑周长约为383 m，开挖面积约为6 183.63 m2，基坑底标高为44.5 m。该工程基坑深度为8 m，为深基坑。该基坑周边情况及基坑分段情况如图2所示。

在基坑开挖范围内出露的岩土层中，主要有杂填土、圆砾和全风化板岩，各岩土层工程特性参数如表1所示。在实际工程应用中，根据不同区段基坑的地质条件和周边环境的不同，采用不同的基坑支护方案，因此实际应用中的基坑一般选用多种支护方案。因为EFGA段外侧为7层银盆大厦，无地下室，大厦边线与基坑边线最近仅为11 m，且用地红线与大厦之间埋设有天然气管道一条，埋置深度约为1.50 m，埋设污水管一条，埋置深度约为1.50 m，需要较严格的位移控制，因此以EFGA段支护方案设计为例进行方案优选。

图2 基坑简易平面图

根据工程地质条件和周边环境情况，初步考虑以下几种支护方案：①桩锚支护A1；②桩+内支撑A2；③双排桩支护A3；④地下连续墙A4。所有方案均采用高压旋喷桩做截水帷幕。

表1 场地各岩土层工程特性参数表

注：*表示变形模量

4.2 确定评价指标属性值

根据实际工程情况和支护方案，计算定量指标C1、C6、C10、C15的取值区间。同时组织5位专家针对定性指标给出评分区间，计算出5位专家的评分区间中最大值和最小值的平均值，从而得到定性指标的属性区间值，如表2所示。

由此可建立区间数决策矩阵C=(cij)m×n。其中，C1、C2、C3、C5、C8、C11、C13、C14为效益型指标，C4、C6、C7、C9、C10、C12、C15为成本型指标，对决策矩阵进行规范化处理可得到规范化区间矩阵R，如式(17)所示。

4.3 确定综合指标值

采用区间层次分析法求得影响因素B1～B4的区间权向量W={[0.230 6,0.308 7],[0.326 1,0.436 5],[0.123 0,0.167 1],[0.174 0,0.236 2]}，以及其所含评价指标区间数评价指标W1={[0.120 8,0.169 8],[0.232 0,0.306 7],[0.085 2,0.120 4],[0.163 6,0.227 8],[0.107 4,0.135 0],[0.145 5,0.190 3]};W2={[0.348 7,0.473 6],[0.282 1,0.303 3],[0.282 1,0.303 3]};W3={[0.113 2,0.128 8],[0.141 0,0.193 1],[0.247 0,0.317 3],[0.161 1,0.223 0],[0.216 2,0.257 5]}。

表2 评价指标区间属性值

(17)

计算各层元素综合排序权重区间，并调整权重中值的取值，可得各评价指标主观权重ω1=(0.039 3,0.073 3,0.027 5,0.053 2,0.032 4,0.045 3,0.159 3,0.111 3,0.111 3,0.016 8,0.023 9,0.040 8,0.027 6,0.033 9,0.204 1)。

运用熵权法得到各评价指标客观权重ω2=(0.053 4,0.066 3,0.063 1,0.001 5,0.068 8,0.103 1,0.083 7,0.115 0,0.025 0,0.063 9,0.109 6,0.016 2,0.065 2,0.054 0,0.111 2)。

基于线性规划的组合赋权法可计算得综合权重ω=(0.046 4,0.069 8,0.045 3,0.027 3,0.050 6,0.074 2,0.121 5,0.113 1,0.068 1,0.040 4,0.066 8,0.028 5,0.046 4,0.044 0,0.157 6)。将综合权重代入式(14)可得到综合指标属性值z={[0.066 2,0.090 0]，[0.076 9,0.011 1]，[0.082 6,0.116 3]，[0.089 2,0.161 7]}。

4.4 方案优选

利用式(15)计算出可能度互补矩阵：

(18)

再由式(16)计算出可能度矩阵排序向量K=(0.363 4,0.263 8,0.227 5,0.145 4)，按照kj的大小排序可得方案排序结果为k1>k2>k3>k4，按照kj越大则方案越优的原则，可以看出方案A1最优。

4.5 灵敏度分析

应用SAATY等提出的灵敏度判断不同决策模型和算法的优劣。假设某决策模型和算法以决策系数δ进行评价，针对δ越大越优的情况(对于δ越小越优的情况，可以用1/δ替换δ)，定义灵敏度η为：

(19)

式中：δmax为决策系数中的最大值，δsec为决策系数中的第二大值。很显然，灵敏度越大，决策模型和算法对方案的决策效果越好。

笔者研究中决策系数为kj，按照式(19)计算本文算法的灵敏度为：

同时，计算得到文献[2]和文献[6]中算法的灵敏度分别为10.37%和22.65%。由此可知，笔者算法较其他决策模型提高了灵敏度，决策结果更加准确、真实可信。

5 结论

基坑支护方案的影响因素存在着较大的不确定性与模糊性，在进行方案评价过程中难以给出确定值。因此，笔者结合区间数理论，探讨区间型指标的基坑支护方案优选问题，并运用区间层次分析法和熵权法确定指标的主观权重和客观权重，利用线性规划的理论进行组合赋权，使得综合权重的赋值更加科学与合理。

笔者在影响指标因素的确定过程中，大量比对国内外文献并结合工程实际情况构建评价指标体系，使评价体系更加全面，提高了评价结果的准确度。针对区间型指标，提出了基于可能度理论的方案排序方法，更能体现基坑支护方案评价中的不确定性，使得评价结果更接近于实际情况，评价模型更加合理化。