追问学生解题失误，思考教学对策

贺育林

摘 要 考试的教学功能之一是查找知识与能力漏洞，通过查阅学生试卷和与部分学生座谈交流，充分了解学生解题时存在的问题，主要是缺乏良好的解题习惯，缺乏思维的深度和严谨性，缺乏综合运用知识的能力，基础知识不扎实，基本技能不熟练。因此，教师应在课堂教学中培养学生的能力，抓基础知识教学，促能力形成;以身示范，培养严谨学风，养成良好的解题习惯;问题驱动，培养思维的深度和严谨性;课堂教学要以学生为中心，充分调动学生思维的积极性。

关键词 解题 失误 对策

中图分类号：G633文献标识码：A

考试的教学功能之一是查找知识与能力漏洞，检测前一段时间的教学效果，使学生逐步适应考试。从一些考试中，我们获取了什么信息？查找到了学生在哪些方面存在漏洞？如何改进今后的教学，是广大教师需要认真思考的问题。

为了充分了解学生存在的问题，笔者通过查阅学生试卷和与部分学生座谈交流，发现学生在考试中存在以下问题：

1学生解题时存在的问题

1.1审题不清，误看条件与问题

表现在审题时阅读速度过快，条件或问题没看清，没仔细的想一想就忽忙作答，以致解题失误。

例1：复数的共轭复数是

（A） （B）（C） （D）

部分学生计算得，而选A。究其原因是没看清题目的问题，要求的是共轭复数，而学生作答是复数。

例2：己知等比数列的各项都为正数，且成等差数列，则的值是

（A） （B） （C） （D）

有的学生通过成等差数列，計算出而选B，没审清题目求的是。

1.2考虑不周全，导致解题错误

表现为大体思路正确，有解题思路与方法，但考虑问题不充分，不周全，因忽略了部分情况或一些细节而导致解题错误。

例3：已知函数 若，则实数的取值范围是 。

有学生解法如下：则或

则当时，解得;当时，解得;

故或

剖析其错误是考虑问题不周全，还有一种情况没考虑到，即当时，即也有可能。

例4：设为数列的前项和，已知，对任意，都有，则的最小值为 。

有的学生根据己知条件求得：;

该学生有一定的基础，与都计算正确，也知道要用基本不等式，出错的原因是：没有考虑到使用基本不等式取“等号”的条件和的要求。

1.3推理意识不强，想当然

表现为解题时不能根据题目条件与问题进行合理的推理论证，而是根据自己的想象凭空猜想而得出结论。

例5：《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥为鳖臑，平面，，，三棱锥的四个顶点都在球的球面上，则球的表面积为

（A） （B） （C）（D）

部分学生认为三棱锥是如图所示几何体，而选择答案D。

解题错误的原因是学生没有进行推理论证，该几何体是否满足鳖臑的条件即四个面都为直角三角形的三棱锥称之为鳖臑。 事实上，上述三棱锥不是鳖臑，不能保证三棱锥的四个面都是直角三角形。

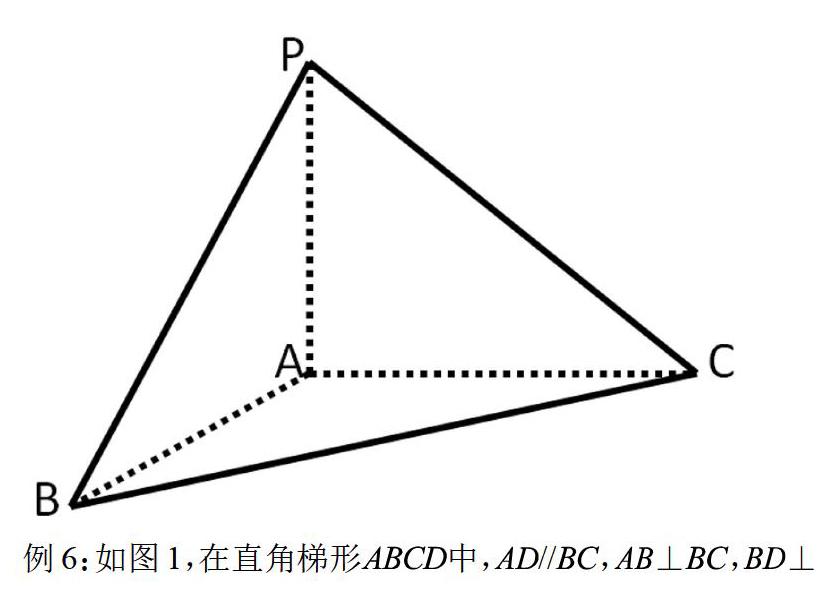
例6：如图1，在直角梯形中，//，⊥，⊥， 点是边的中点， 将△沿折起，使平面⊥平面，连接，，，得到如图2所示的几何体。

（Ⅰ） 求证：⊥平面;

（Ⅱ） 若，二面角的平面角的正切值为，求二面角的余弦值。

大部分学生能顺利做出第一问，部分学生根据二面角的平面角的正切值为，能分析出，但由于长度未知。他就乱写一个数学或字母，然后建系求解，运算量非常繁杂且算不出结果。究其原因是：不会运用题目已知条件//，⊥，⊥，推证出两个三角形相似，从而推导出。

1.4解题方法选择不合理，费时费力

表现为解题时不能抓住关健条件，进行合理的推理运算，或不能根据选择题、填空题的特点，进行合情推理。

例7：如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的正视图（等腰直角三角形）和侧视图，且该几何体的体积为，则该几何体的俯视图可以是：

有学生根据、、、四个选择支的俯视图画出原几何图形，再依据己知求得几何体的体积的，而选择出正确答案，尽管答案对了，但画四个几何体，浪费了大量时间，有点得不偿失。事实上，本题只需借助正方体，依据侧视图及体积就可知它是一个底面积为4的四棱维，从而快速解答。

例8：已知函数，则的值为

（A）（B）（C）（D）

有同学在解答此题时，去求的导数，画出的图象，但还是一愁莫展，殊不知只需思考所求结论，联想到，抽象出是否为定值，再特值求解，很快得出结论。

1.5书写不规范，导致失分

表现在做解答题时，必要的解题步骤没写或没有做到步步有据，因缺乏必须的解题步骤而导致失分。

例9：近年来，我国电子商务蓬勃发展。2016年“618”期间，某网购平台的销售业绩高达516亿元人民币，与此同时，相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易，并对其评价进行统计，网购者对商品的满意率为0.6，对服务的满意率为0.75，其中对商品和服务都满意的交易为80次。

（Ⅰ） 根据已知条件完成下面的22列联表，并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”？

（Ⅱ）

若将频率视为概率，某人在该网购平台上进行的3次购物中，设对商品和服务都满意的次数为随机变量x，求x的分布列和数学期望Ex。

有的学生在做第（Ⅱ）问时，直接列出x的分布，求出数学期望。尽管此学生理解题意，也具备解此题的能力，但由于书写不规范而失去了大量的分数。原因是：要求随机变量x的分布列，必须说明随机变量可取哪些值，并计算取这些值的概率是多少，有了这些，才能列出随机变量x的分布列，这就是说解题时要有理有据，不能没有解决问题的过程。

1.6解题心理性失误

表现为根据平时考试经验，自设一个难度表，自认为哪些题号比较难，难以做对，做试卷时遇到这些题号的题不看也不做，直接跳过。

如有的同学认为选择题11题、12题、填空题16题很难，直接不做，或乱选一个答案，事实上，并不是每次考试中的这三题都是非常难，只要认真思考或许可以做对，学生失去了宝贵的得分机会。

2剖析失误的成因

分析学生以上解题失误原因，可能主要存在以下的几个问题：

2.1有的学生缺乏良好的解题习惯

主要表现在审题不仔细，书写不规范，平时做题时，只重数量（做题的量多），不重质量。缺乏解前分析，解后反思。面对错误往往归因为粗心，只是计算上范了低级错误而已。没有重视因基本概念模糊不清而引起的错误，没有对平时的错误进行深入的追究，不能抓住问题的本质回到概念中去解题、去思考。

2.2有的学生缺乏思维的深度

学生平时学习时只停留在“听懂”、“看懂”层面，未能真正理解知识、原理、方法，数学学习只停留在表面，没有从实质上进一步深入研究，更不能熟练运用。如果在平时学习中能把每块知识，每道题目，认真反复地琢磨一遍，好好想一想其中的来龙去脉，而不是“是懂非懂”的浮在表面，则经过长期的深度思维的积累，数学能力就会功到自然成。

2.3有的学生缺乏思維的严谨性

为什么有学生在做题时，不写关键的步骤，或将关健步骤省略。一方面，是不讲道理的“想当然”，另一方面，不是不想写，而是根本没想到这关键的一步。究其原因是缺乏思维的严谨性。数学是一门思维科学，培养学生具有优秀的思维品质是数学教学的重任。思维的的严谨性、广阔性、灵活性等是重要的思维品质。

2.4有的学生缺乏综合运用知识的能力

学生面对一个稍微复杂的问题时，不会寻找突破口，不会利用以往的解题经验去发现或试图转化为己学知识去解决，但如果将问题分成几个小问题或几个知识块让学生逐个去解决，往往能得到相应的结果。为什么综合起来或者换一种形式，学生就对问题的解决就摸不着头脑了，主要的思维节点在于缺乏思维的变通性，不会将原问题化归为己经解决过的问题，不具备综合运用知识解决问题及探寻新的解决策略的能力。

2.5有的学生基础知识不扎实，基本技能不熟练，能力不够强

解题失误很多是因为基础不扎实，基本技能不熟练造成的。高考题大多是综合性问题，学生因某个知识缺乏必然导致解题不能顺利完成，为此需查漏补缺。有时是能力不到位，因运算能力不强而影响速度与准确度;因阅读理解能力弱而不理解题意导致解题失误;因思维能力欠佳而缺乏分析综合性问题的能力而导致解综合题失误。

3思考解决问题的对策

面对学生的问题，距离高考又只有几十天时间，如何帮助学生呢，如何改进自己的教学呢？笔者认为：关键是要在课堂教学中培养学生的能力。具体做法如下：

3.1抓基础知识教学，促能力形成

基础知识教学应长抓不懈，对基本概念、基本方法应通过变式教学使学生理解并掌握。变式教学的核心是利用构造一系列变式的方法，来展示知识发生、发展过程，数学问题的结构和演变过程，解决问题的思维过程，以及创设暴露思维障碍情境，从而形成思维训练的有效模式。通过变式教学，凝聚学生的注意力，培养学生在相同条件下的迁移、发散能力，激发学习热情，达到举一反三，触类旁通的效果，使学生对基本概念的理解更深刻，对基本技能的掌握更准。课堂上对学生易错的概念，理解不透的方法应通过不断的变式、变形、变换让学生理解并掌握。

3.2以身示范，培养严谨学风，养成良好的解题习惯

课堂教学中，提出问题或出示习题后应先让学生独立思考，让学生独立地去审题，去解题，然后通过追问让学生体验怎样根据己知条件，一步一步的推理分析，从而建立已知与结论之间的联系。对解题中的关键步骤要通过追问，让学生理解，以防“是是而非”。对解题步骤，每节课教师应至少板书一道题的完整解答过程，剖析得分点与知识点，让学生理解什么步骤一定要书写。解完题后要进行反思：此题入手点是如何想到的？还有其它解法吗？有其它问法吗？与做过的什么题有联系？有哪些转化过程？还能设计什么问题？使学生养成解题后反思习惯。

3.3问题驱动，培养思维的深度

二轮复习，重在知识点的梳理上，要注意站在更高的角度引导学生将所学知识进行联珠编网，沟通知识之间的内在联系，以主干知识为主线促进高中知识的条理化、网络化;重在解题方法的归类总结上，即在讲评时，要引导学生对解题方法进行归类总结，以达到触类旁通的效果。

3.4课堂教学要以学生为中心，充分调动学生思维的积极性

课堂教学要树立以学生为中心的观念。问题设计依学生的能力设计，让学生有研讨、交流的时间与空间，让学生学会质疑问难。习题的讲解要顺从学生的思维，依学生的思维进行启发、诱导，而不要强制“灌输”，可将教师的解法与学生进行对比、交流。要重视教学过程，讲清概念、公式的来龙去脉，解题思路的获取过程，错误解法的错因。

参考文献

[1] 陈涛.高中数学解题失误的分析及策略[J].学周刊，2013（10）：128.