桩基侧阻力快速确定方法讨论
(贵州大学 土木工程学院,贵阳 550025)
1 研究背景
在桩基工程中,对于桩土(岩)组合结构而言,由于岩(土)体离散性以及桩土(岩)接触面复杂相互作用等因素的影响,按照规范法每一次试桩试验只能确定一根桩的侧阻力,比较繁琐且不够经济。因此,有必要对所测桩土(岩)组合结构的力学参数展开研究,以寻求一种简单适用的桩基侧阻力确定方法。
目前国内外众多学者基于连续介质力学理论和非连续介质理论及桩基施工工艺等,对桩基的静、动力学特性进行了深入研究。
(1)连续介质力学理论方面:程昌钧等[1]将桩土系统看成半无限空间黏弹性体,利用应力-应变协调条件,在空间柱坐标系中研究岩土对桩基的抗力和各种端部条件下桩基的刚度;Koo等[2]研究了桩-土上部结构动力相互作用;Wong等[3]建立了水平振动下桩土非线性相互作用的力学模型;陆建飞等[4]研究了饱和层状两相介质固结和流变作用下桩的动力行为。
(2)非连续介质理论方面:Matlock[5]和Reese等[6]利用综合反映土体的非线性、桩基刚度和外荷载特点的土体抗力集度P和桩基相对应点挠度y曲线,计算了桩基的内力和变形;Mylonakis等[7]给出了双层土地基中相互作用因子和群桩水平动力阻抗的计算方法;黄茂松等[8]采用动力Winkler 地基模型模拟了桩土的动力相互作用,并运用传递矩阵法考虑地基土的分层特性,计算了群桩水平动力阻抗和桩身内力;Zertsalov等[9]研究表明,桩的承载力不仅取决于地基的抗压承载力,同时也受到了桩的埋置深度、岩(土)体的压缩模量、桩体的弹性模量以及桩侧阻力的影响。
(3)施工工艺方面:蔡江东等[10]研究了桩土界面特性以及界面上正应力对桩基侧阻力的影响;张利新[11]利用不同的注浆施工工况,对试桩桩侧埋设的钢筋计的测试结果进行分析,得到不同土层在注浆后的极限侧阻力增强系数,推断出抗压桩端阻力增强系数,得到了实测值与规范值之间的对应关系。然而,在桩土(岩)接触面的复杂相互作用情况下,桩基的力学特性研究仍有许多理论难点有待突破。
从已有的研究成果来看,对桩基动、静力学特性的研究,多集中于桩土(岩)相互作用的静力非线性和动力非线性方面。鉴于此,本文采用连续介质理论,同时考虑桩土(岩)接触面间的变形协调关系,将桩基看作由不同刚度地质材料组成的层状体,利用规范法与理论相结合,通过桩基试验得到桩土(岩)力学参数,建立了快速确定桩基侧阻力的模型,对层状桩土(岩)体问题求解过程中的适用性进行模型验证。验证表明,该模型利用单桩试验数据对现场每一根桩的侧阻力预测是较为准确的,可为类似工程所使用。
2 桩基侧阻力承载机制
桩周土(岩)体压密、弹性变形、弹塑性变形及破坏通过桩土(岩)间的剪切作用发生[12]。桩与土(岩)体界面上剪应力首先达到弹性极限值τmax,然后岩土体将剪应力传递给相邻单元,这一过程连续传递于m倍基桩直径外,直至剪应力最终趋于0(根据《建筑桩基技术规范》(JGJ 94—2008)[13],可认为m=5.5d,d为桩径)。为简化起见,假定基桩周围土(岩)体剪应力为三角形分布,即桩与土(岩)体界面上的剪应力最大,m倍基桩直径处剪应力为0,如图1所示。
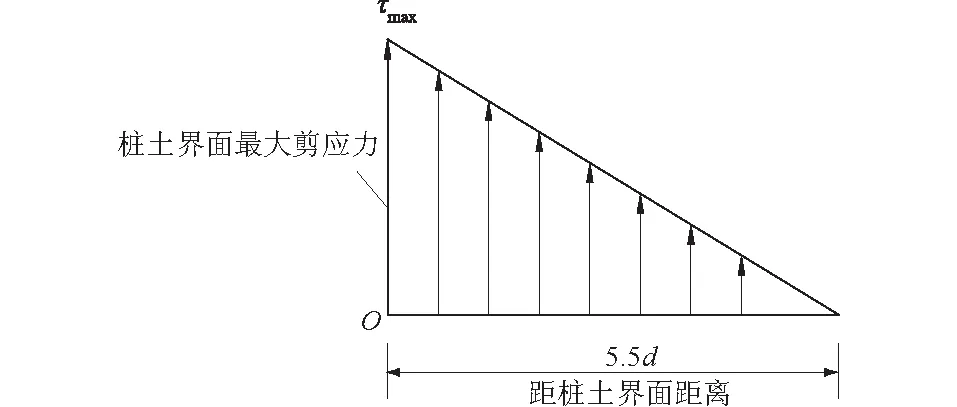
图1 剪应力传递简化模型Fig.1 Simplified model of the transfer of shearing force along the pile
3 桩土(岩)复合体理论分析
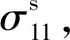
对如图2所示的桩土(岩)复合体连续介质单元假定:①桩体和桩周土(岩)体均为各向同性线弹性体;②桩土(岩)变形稳定时属小变形;③桩土(岩)复合体变形处于极限平衡时桩土(岩)界面不分离,但土(岩)、桩的变形趋势相差n倍。n与桩土(岩)复合体性质有关,且土(岩)与桩弹性模量相差越大,n越大;相差越小,则越趋近于1,可通过数值拟合方法获得。由广义胡克定律及应力-应变叠加原理,可得桩土(岩)复合体连续介质弹性本构方程[15],即:
(1)
(2)
(3)
(4)
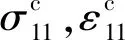
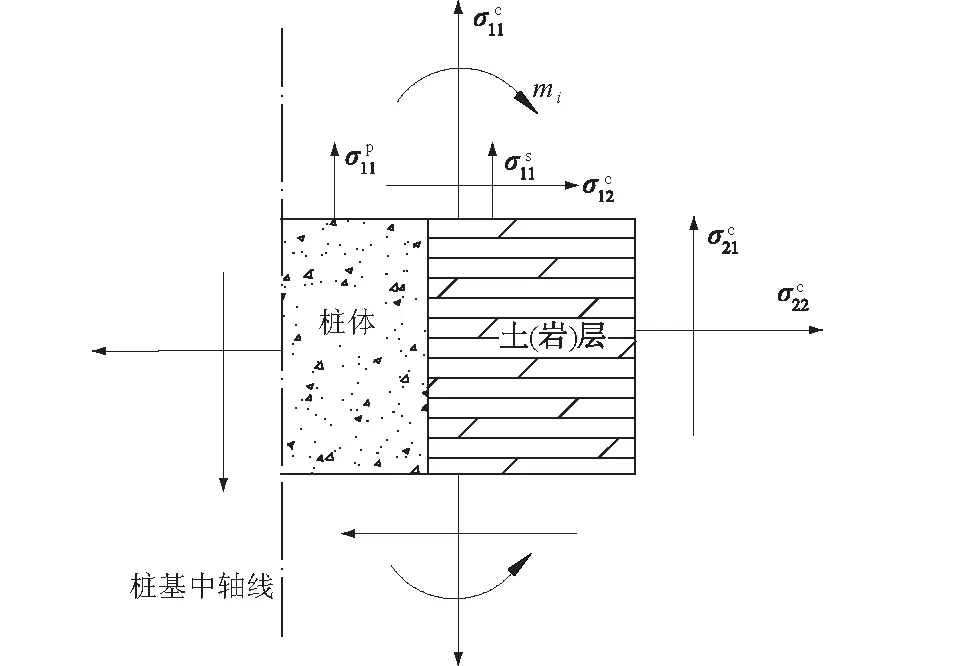
注:为微元体的切应力;mi为叠加后的合力矩。图2 理论分析微元体Fig.2 Element volume of continuous medium
对如图2所示的土(岩)层和桩体,分别由弹性理论可得:
(5)
(6)
(7)
(8)
式中:υs,υp分别为土(岩)和桩身的泊松比;Es,Ep分别为土(岩)和桩身的弹性模量。联立式(1) —式 (8),可得桩土(岩)复合体的本构关系为
(9)
其中:
D11=(αpEp+nαsEs)-1;
D12=-(αpυp+αsυs)D11;
D21=-(αpυp+nαsυs)D11;
联立式(1)、式(2)、式(3)、式(5)、式(7)、式(9)可得桩土(岩)剪应力为
4 桩基侧阻力的初探
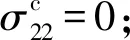
4.1 当桩基相互无影响时
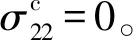
(11)
图3(a)、图3(b)分别为Es/Ep=0.001,n=15时及Es/Ep=0.001,L=4时,桩基侧阻力变化趋势(为计算方便,假定ψsi=βsi=1.0)。从图3(a)可以看出:土(岩)与桩的弹性模量比Es/Ep恒定条件下,桩侧阻力随L增加而提高;从图3(b)可以看出:土(岩)与桩的弹性模量比Es/Ep恒定条件下,桩侧阻力随n增加而提高。

图3 桩基侧阻力与L和n的关系(Es/Ep=0.001)Fig.3 Relation of side resistance against L and n (Es/Ep=0.001)

图4 桩基侧阻力与Es/Ep的关系(L=4,n=20)Fig.4 Relation between side resistance and Es/Ep (L=4,n=20)
图4为n=20,L=4时,桩基侧阻力变化趋势(为计算方便,假定ψsi=βsi=1.0)。可以看出:桩基侧阻力随Es/Ep增大而逐渐提高,即桩身混凝土强度等级降低或桩周土(岩)弹性模量提高,都会使桩基侧阻力增加,且Es/Ep越大,桩基侧阻力变化越明显。由此可见,提高桩身混凝土强度等级,有可能导致桩基侧阻力降低,但通过后注浆等技术方法可以明显提高桩基侧阻力。
4.2 当桩基相互影响时
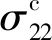
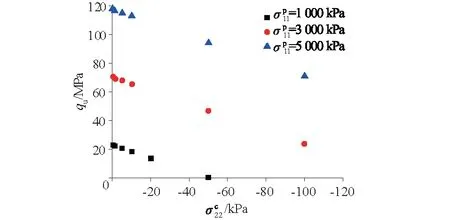
图5 桩基侧阻力与的关系(L=4,n=20)Fig.5 Relation between side resistance and (L=4,n=20)

5 本文方法适用性验证
5.1 试桩资料
富源路A地块的A1栋塔桩基础为冲孔灌注桩。施工时采用泥浆护壁与低锤密击的方法,并及时添加片石、砂砾使孔壁挤压密实,每冲击1~2 m,排渣一次,并定时补浆,直至设计深度;采用桩端、桩侧复式后注浆技术,在桩底和桩侧分别10,18,27 m各设一道桩侧压浆管。
2根试桩桩长35.0 m、桩径1.2 m,桩周地层岩性基本一致,但桩底支承条件有所不同(1#试桩底为黏性土;2#试桩底依次为厚度3.5 m的黏土层与约26 m的淤泥质黏土层)。地基土物理力学参数如表1所示,其中土体的弹性模量E为3个试样的平均值,0~-6.5 m(原地面为0 m)的弹性模量E由重塑土测试而得。每根试桩设置8个断面,每个断面埋设3个钢筋应力计进行数据采集。其中桩身轴力分布如图6所示。

表1 桩周土体物理力学参数Table 1 Physico-mechanical parameters of soil layers
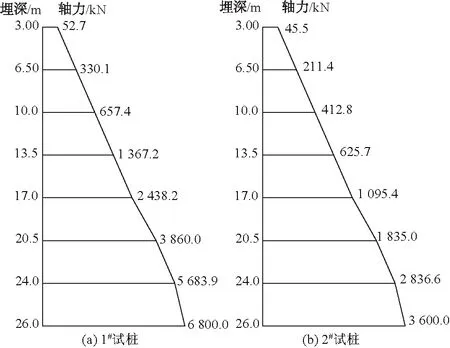
图6 桩身轴力分布Fig.6 Axial stress distribution of piles
5.2 侧阻力计算方法验证
为验证连续介质理论建立侧阻力的计算公式在桩基侧阻力分析中的有效性与合理性,利用规范法[13,16]与本文方法对工程试桩进行了计算,并对结果进行了比较分析。计算的结果如表2、图7所示。
由于本文方法与规范法计算的理论值较为接近,图7仅表示了L=3,n=27条件下,本文方法计算结果与规范法计算结果对比。
由本文计算方法与规范法[13,16]计算结果可以看出:①从桩埋深来看,距荷载箱越近,桩基侧阻力极限值计算越精确,误差越小;②与1#试桩相比,2#试桩(桩底为淤泥质黏土层)计算精度更高;③1#和2#试桩计算结果可以说明当桩底存在软弱夹层时,参数L和n可近似看作常数;而桩底无软弱层时,参数L和n随距荷载箱距离的增大而增大。④利用试桩数据拟合的参数L和n,并结合岩土工程勘察阶段土(岩)体的弹性模量,即可获得场地每根桩的侧阻力分布规律,为桩基的设计提供依据。

表2 2根试桩桩基侧阻力规范法与本文方法计算结果对比Table 2 Comparison of side resistance calculated by specification approach and the method in this paper
6 结 论
(1)将桩基看作由不同刚度地质材料组成的整体,基于连续介质理论的正应力-应变关系,建立了快速确定桩基侧阻力计算公式。该方法可计算单桩与疏桩的侧阻力,也可对存在挤土效应桩基的侧阻力进行计算。
(2)从计算结果对比分析可以看出,桩基侧阻力随Es/Ep增大而提高,即桩身混凝土强度等级降低或桩周土(岩)弹性模量提高,都会使桩基侧阻力增加,且Es/Ep越大,桩基侧阻力变化越明显。
(3)由规范法与本文方法计算试桩侧阻力的结果对比分析可以看出,本文方法计算的结果较为可信。因此,可以利用连续介质理论计算方法对类似场地工程桩侧阻力进行预测,且这种预测是快速、可行和有效的。

