基于快速控制电源的IGBT结温分析

宋德勇，高 格，杨申申

基于快速控制电源的IGBT结温分析

宋德勇1，高 格2，杨申申1

（1. 中国船舶科学研究中心，江苏无锡 214082；2. 中国科学院等离子体物理研究所，合肥 230031）

快速控制电源同时运行的IGBT器件数量多，输出信号需要快速响应不同的给定信号。针对其工作特点，通过理论计算、MATLAB模型及有限元模型仿真，研究了典型工况下IGBT的结温分布特点，并揭示了该工况下由热载荷导致的IGBT结构变化，对后续研究IGBT可靠性提供了依据。

快速控制电源；IGBT结温；有限元

0 引言

EAST装置为磁约束核聚变托卡马克装置，16个RMP线圈被放置在EAST装置内真空室中来进行边界局域模等相关研究[1,2]。现有8套完全相同的RMP线圈电源，每套电源为2个串联的线圈供电[3]。该电源为典型的快速控制电源，响应时间小于0.25 ms。对于1套电源，一共有48个IGBT模块，即8套电源共384个IGBT模块。在8套电源同时运行时，研究所有IGBT模块的可靠性显得尤为重要，在这种特殊的工况下，需要研究电源中IGBT器件的可靠性相关的参数，而主要工作是分析IGBT的结温分布[4]。

1 快速控制电源工作模式

快速控制电源拓扑结构为典型的AC-DC- AC结构[5]，AC-DC部分为三相不控整流桥，每个整流桥为一个单独的DC-AC部分的H桥提供母线电压，逆变部分主体为H桥两串三并结构。对于每一个H桥，左右桥臂分别由4个IGBT半桥模块并联，IGBT的开关频率为10 kHz，通过载波移相，等效开关频率达到120 kHz[6]。

电源的具体输出参数如表1所示，额定输出值为4000 A/450 V，延迟时间为从给定信号发出到输出值上升到额定值的50%时的时间。电源的主要运行工况为脉冲电流和正弦电流，脉冲电流工况下，脉宽、幅值及上升时间均会发生变化，正弦工况下，周期及幅值均会发生变化。

表1 快速控制电源输出参数

IGBT作为电源中的主要电力电子器件，其失效原因较多，其中热疲劳最为常见，而高温导致的失效在所有电子设备失效中所占的比例大于50％[7]，故需要重点分析IGBT的结温特点。在目前对IGBT可靠性的研究中，主要的寿命预测公式均提到结温平均值和结温纹波对寿命的影响[8]，基于本电源的快速响应特点，主要考虑结温纹波的影响。

2 IGBT结温分析

2.1 理论计算

根据该型号IGBT数据手册，额定输出电流I=4000 A，母线电压U=340 V，开关频率f=10 kHz，负载直流阻抗R=32 mΩ，假定并联的IGBT之间不均流度=6%，并联支路不均流度=5%，计算方法[9][10]如式(1)-(8)所示：

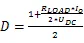
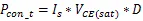
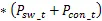
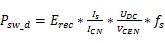
上述公式中，I为单个IGBT的电流，为IGBT占空比，P和P为IGBT的开关损耗和通态损耗，分别为245.65 W和351.14 W，P和P为二极管的开关损耗和反向恢复损耗，分别为64.59 W和228.17 W，∆T和∆T分别为IGBT和二极管的结温温升，结果为70.42 K和58.55 K。

上述计算可以看出IGBT和二极管结温温升平均值主要取决于输入电流值、工作电压、开关频率以及电流的占空比，输入电流、工作电压越大，则IGBT和二极管的工作条件越苛刻，其结温温升会越高；开关频率越高，说明电子器件动作越频繁，开关损耗会越高，导致IGBT和二极管的结温温升越高；占空比越大，说明IGBT每个电流周期内工作时间越长，其结温温升也会越高，同时二极管结温温升越低。

2.2 MATLAB模型仿真

2.2.1 单脉冲工况

如图1所示，由热阻抗等效图，可将IGBT的热阻模型等效为电路模型[11]，在MATLAB中搭建电路进行仿真，热阻抗参数如表2所示。

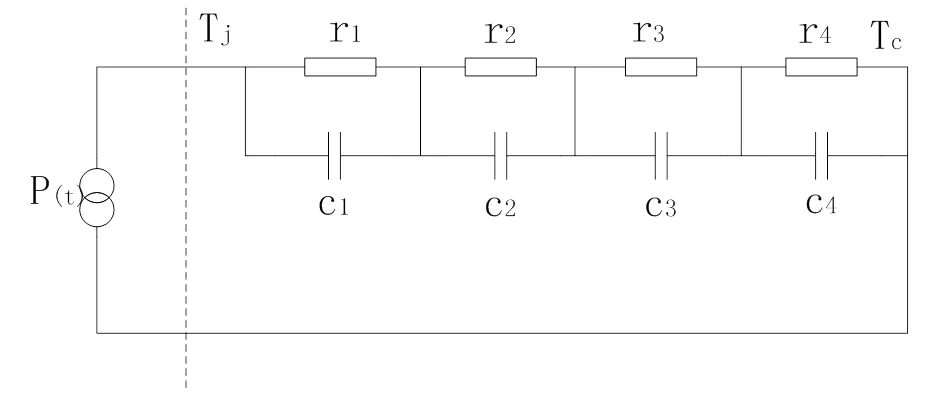
图1 IGBT模块热阻抗等效图

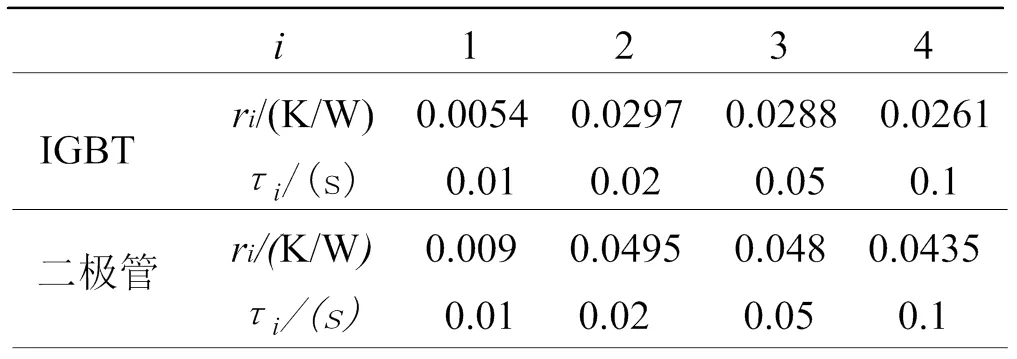
表2 IGBT模块热阻抗参数

如图2所示，输出直流4000 A电流时，IGBT管芯最高温升为70.16 K，二极管管芯最高温升为58.68 K，变化趋势均与瞬态阻抗曲线一致，仿真结果也与理论计算一致。为了考察IGBT模块瞬态情况下的承受电流能力，只需分析IGBT的温升即可。

2.2.2 多周期脉冲工况

IGBT结温的上升是由于工作时的功率损耗引起的[12]，幅值为P的矩形单脉冲或间隔时间足够长的连续脉冲作用于IGBT芯片时，所引起的IGBT结温T自初始温度T的变化如图3所示。

结温经过足够长的时间能回到初始温度，但是，当IGBT处在连续导通一串脉冲的PWM工作方式下，且连续脉冲的间隔时间不足以使结温恢复到初始值，此时IGBT结温在连续脉冲的反复作用下累积叠加上升，在经过一个逐步上升的过程后，结温围绕着一个恒定的平均温度T做近似等幅波动，此时热量的产生与散失达到了动态平衡[13]。

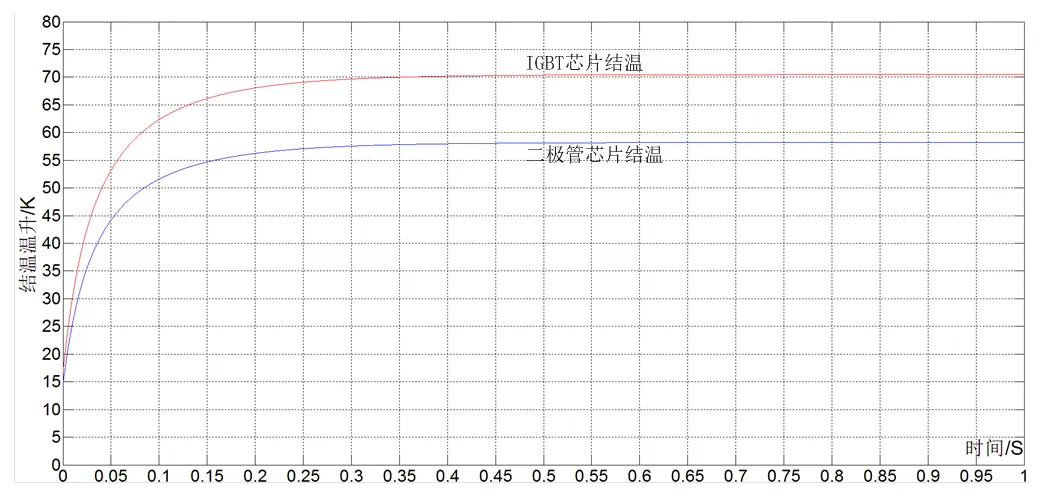
图2 IGBT模块结温温升曲线

图3 结温叠加上升过程

假定此脉冲功率周期为0，每个周期内脉冲作用时间为tp，无脉冲时间为t，将初始壳温0作为零刻度，脉冲功率不作用期间结温只是零输入响应，脉冲功率作用期间结温是一个零输入响应和一个零状态响应相加的全响应[14]。

根据IGBT的热阻热容等效为电路中的电阻电容，将脉冲功率作为一个电流源激励，结温在受到功率脉冲周期作用后的变化[15]如下：

第一个脉冲周期结束后结温：

以此类推，第n个脉冲周期结束后结温：

当n→∞，结温进入稳定的等幅波动状态，递推可得，第n个脉冲周期结束后结温：

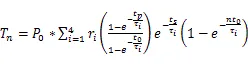
在任意一个周期内的结温：

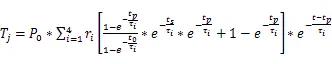
结温最小值、最大值、纹波：

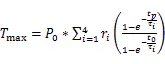
由图4可以看出，脉冲功率值恒定时，IGBT结温纹波与输入电流周期及占空比都有关。

输入电流周期固定时，占空比在从0增大到1的过程中，结温纹波初始阶段增大，进入一段时间的平顶部分然后又逐渐减小，整体呈对称变化趋势，同时输入电流周期越小，其结温纹波的绝对最大值也越小，且结温纹波到达最大值的时间越长，具体二维曲线如图5所示。

占空比固定时，输入电流周期越大即频率越低时，结温纹波越大，且结温纹波在占空比为0.5时上升最快，在占空比小于或大于0.5时上升均变慢，并呈对称分布，具体二维曲线如图6所示。

设定环境温度为30℃，在MATLAB仿真模型中改变输出电流频率和占空比，得到如表3所示结果。在仅有输出电流频率发生改变时，温升平均值不变，但结温纹波发生变化，频率越低，结温纹波越大，这与理论分析完全一致。

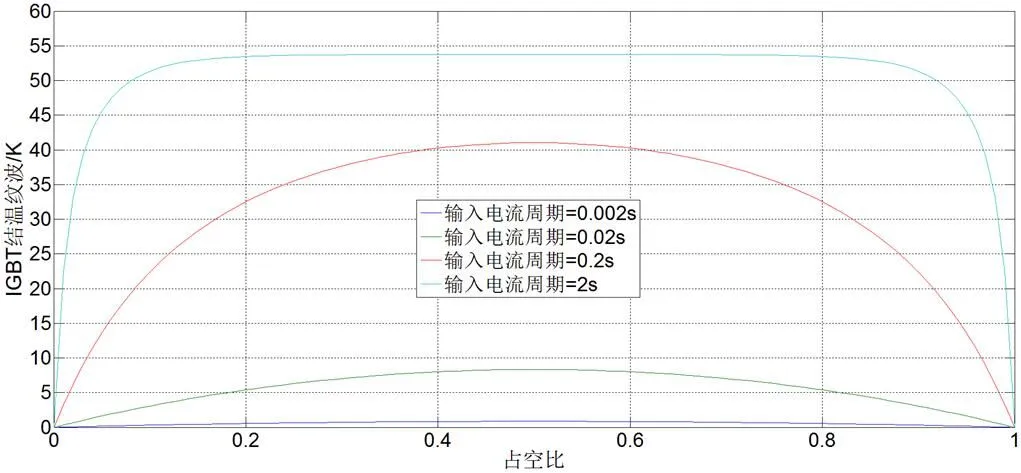
图5 不同电流周期下IGBT结温纹波与占空比关系

图6 不同占空比下IGBT结温纹波与电流频率关系

表3 不同频率电流下IGBT结温

如表4所示，在仅有占空比发生改变时，器件的温升平均值随占空比的增大而增大，同时器件的结温纹波在占空比为0.5时为最大，在低于或高于0.5时均呈下降趋势，关于占空比为0.5时的结温纹波呈对称分布，与理论分析一致。

表4 不同占空比电流下IGBT结温

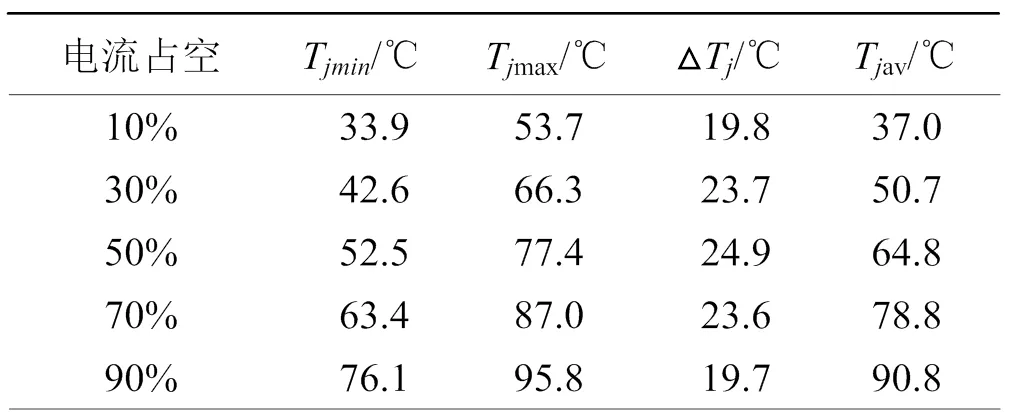
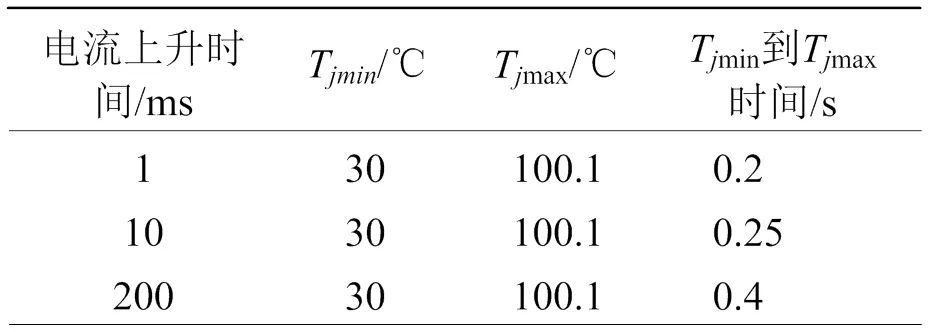
如表5所示，同频率的脉冲电流，在电流上升时间变长时，IGBT结温从最小值到最大值的上升时间变长，即IGBT由脉冲电流工况向近似正弦电流工况转变。

2.3 有限元模型仿真

针对型号为英飞凌FF600R06ME3的IGBT模块，建立其三维模型[16]，由封装模型简化为最简单的分层模型，以有限元的思想，在workbench中进行热-结构耦合分析[17,18]，图7为此IGBT的分层结构示意图。

表5 不同上升时间电流下IGBT结温

由于该IGBT内部由3个完全相同的部分组成，实际仿真时提取其三分之一。根据计算，在4000 A情况下，IGBT总损耗为596.79 W，故对一个IGBT芯片上表面施加5 Hz的200 W功率，铜底板下底面设定对流换热系数[19]为4320 W/(m2*℃)，其它面为绝热，环境温度为30 ℃，瞬态加热时长为2 s。

在瞬态条件下，IGBT 结温曲线如图8所示，红色曲线为最低温度，绿色曲线为最高温度，最高温度位于被加热的IGBT芯片上表面，为86.15 ℃，结温纹波为56.15 ℃，与上述结温仿真结果(57.5 ℃)基本一致。

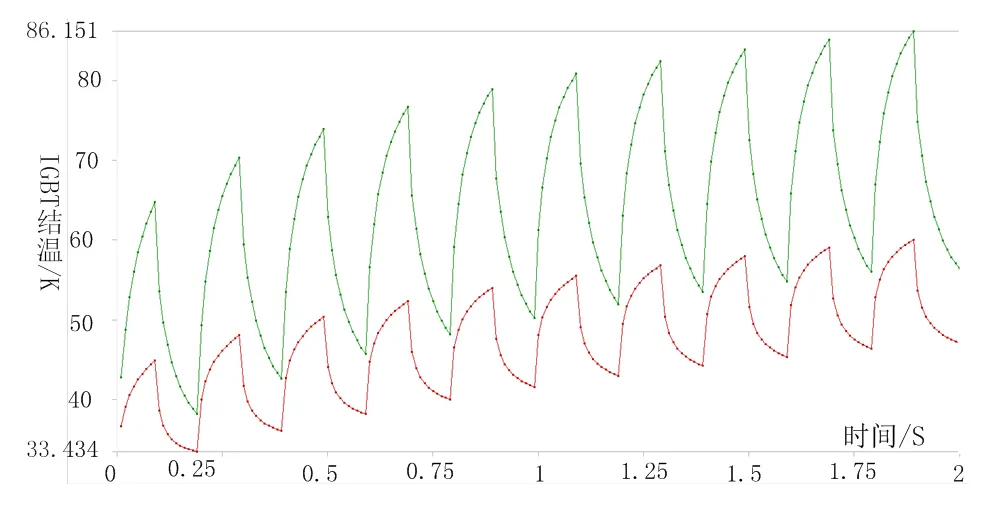
图8 IGBT结温曲线

IGBT模块的应力分布从芯片到底板呈现出非线性变化，且形变最大值为11.59 μm，出现在键合线处，如图9所示，说明在瞬态加热功率条件下，键合线容易首先变形，使其与芯片上表面间的接触不牢固，出现断裂现象，这是因为键合线的热膨胀系数远大于IGBT芯片，在受到周期性热应力冲击时，由于两者之间热膨胀系数匹配较差，热应力长期冲击最终导致键合线失效。

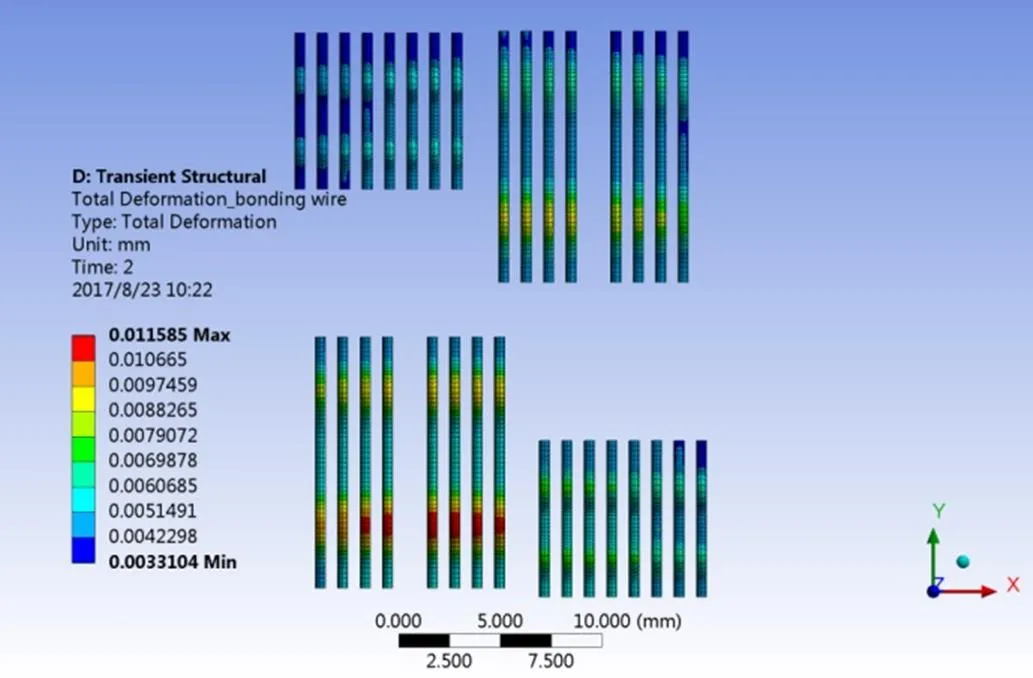
图9 IGBT模块形变分布

3 总结

EAST装置上应用于快速控制电源的IGBT工况非常特殊，实际工作时输出电流的幅值、频率、占空比和上升时间均会发生变化，在不同的工况下，IGBT的结温平均值和结温纹波会发生变化。

综上所述，脉冲工况需要考虑上升时间、电流频率、电流幅值、开关频率和占空比5个因素对结温温升或结温纹波的影响，这也是影响IGBT可靠性的因素，且脉冲工况下IGBT键合线的形变最大，是失效的主要环节。长上升时间、高电流频率、低电流幅值、低开关频率和低占空比更有利于延长IGBT的使用寿命。实际应用时，开关频率、电流幅值基本不变，因此需要重点关注上升时间、电流频率和占空比对IGBT寿命的影响。

[1] 郝长端．J_TEXT托卡马克共振磁扰动线圈的电磁结构分析和热分析[D]．武汉: 华中科技大学，2011．

[2] V．Toigo, E．Gaio, R．Piovan, et al． Overview on the power supply systems for plasma instabilities control[J]．Fusion Engineering and Design, 2011, 86: 565-571．

[3] 宋德勇, 高格, 傅鹏等. EAST装置RMP线圈电源的优化设计[J]．核聚变与等离子体物理, 2017, 37(2): 199-203．

[4] 周雒维, 吴军科, 杜雄等. 功率变流器的可靠性研究现状及展望[J]．电源学报, 2013, 1: 1-15．

[5] Deyong Song,Peng Fu,Ge Gao, et al．The Harmonic Analysis of RMP Coil Power Supply in EAST TOKAMAK [J]．Journal of Fusion Energy, 2016, 35(3): 550-555．

[6] 宋德勇. EAST托卡马克共振磁扰动线圈电源设计分析研究[D]. 合肥: 中国科学技术大学, 2017.

[7] 潘洋. IGBT封装模块散热特性的研究[D]．武汉: 华中科技大学, 2013．

[8] 赖伟, 陈民铀, 冉立, 等. 老化实验条件下的IGBT寿命预测模型[J]．电工技术学报, 2016, 31(24): 173-180．

[9] 谢勤岚, 陈红. PWM逆变器中IGBT的损耗计算[J]．中南民族大学学报, 2003, 22(1): 39-41．

[10] 张明元, 沈建清, 李卫超等. 一种快速IGBT损耗计算方法[J]．船电技术, 2009, 29: 33-36．

[11] 鲁光祝. IGBT功率模块寿命预测技术研究[D]．重庆: 重庆大学, 2012．

[12] 陈明, 胡安, 唐勇等. 绝缘栅双极型晶体管脉冲工作时结温特性及温度分布研究[J]．西安交通大学学报, 2012, 46(4): 70-76．

[13] 刘辉. 等离子体垂直位移快速控制电源关键技术研究[D]．北京: 中国科学院大学, 2014．

[14] 颜秋容, 谭丹. 电路理论[M]．北京: 电子工业出版社, 2009．

[15] 侯少敏. 高速动车组变流系统损耗分析与散热研究[D]．北京: 北京交通大学, 2011．

[16] 余小玲. 电力电子集成模块及新型翅柱复合型散热器的传热性能研究[D]．西安: 西安交通大学, 2005．

[17] 熊文雯, 张小玲, 谢雪松等. 基于结构函数的IGBT热特性研究[J]．电力电子技术, 50(12), 11-14, 2016．

[18] 张薷方. 基于有限元法的IGBT模块封装散热性能及热应力的仿真研究[D]．重庆: 重庆大学, 2015．

[19] 陈永淑. IGBT的可靠性模型研究[D]．重庆: 重庆大学, 2010．

Analysis of IGBT Junction Temperature Based on Fast Control Power Supply

Song Deyong1, Gao Ge2, Yang Shenshen1

(1. China Ship Scientific Research Center, Wuxi 214082, Jiangsu, China; 2. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China)

TN86

A

1003-4862（2019）10-0001-05

2019-04-19

国家磁约束核聚变能发展研究专项 (基金编号2013GB102003)

宋德勇（1990-），男，工程师。研究方向：电力电子器件应用。E-mail: dysong1990@163.com