基于自适应神经网络的电力系统经济调度

孙 勇

基于自适应神经网络的电力系统经济调度

孙 勇

(南京电子技术研究所，南京 210039)

为了适应新能源接入大电网的发展趋势，降低输电损耗，提出了考虑输电损耗的电力系统经济调度问题。提出根据功率平衡约束误差在线调整连续神经元更新步长的自适应方法，建立了基于增广的Lagrange-Hopfield神经网络的自适应神经网络算法，并且构建了该算法的仿真计算流程。从理论上证明了该算法的收敛性，论证了该算法具有快速的收敛速度。通过选取不同的更新步长参数求解实例，证明该算法可以在线调整步长，从而提高收敛速度，大幅减少迭代次数。

经济调度 神经网络 输电损耗 迭代次数

0 引言

新能源的应用在一定程度上缓解了目前全世界范围内面临的能源压力，但是也带来一些新的问题，其中经济调度问题是电力系统中比较有难度的数学优化问题，即在满足多种电力系统运行约束的条件下，使得总发电成本最小化[1]。特别是新能源接入条件下，对电力系统的快速调度有了更迫切的要求，由于电力系统经济调度问题是一个复杂的非线性优化问题，传统的Lagrangian乘子法、内点法和梯度下降法等基本的优化算法难以适应非线性约束条件下具有大规模变量的非线性优化问题。

因此，许多学者提出应用智能优化算法求解电力系统的经济调度问题。例如，朱继忠等人利用改进的内点法求解多能源综合经济调度问题[2]。郑晓菁、吴亮红等人分别采用人工蜂群优化算法和自适应差分进化算法解决复杂电力系统的经济调度问题[3,4]。王凌和Yousefi等针对电力系统经济负荷分配分别提出一种基于混合双种群的差分进化算法和一种改进的粒子群优化算法[5,6]。Zou 等提出一种改进的差分进化算法用于解决经济负载调度问题[7]。在这些群智能优化算法中，粒子群优化算法 (Particle Swarm Optimization,PSO)具有易于实现的优点。然而 PSO算法在处理具有连续的复杂约束的电力系统经济调度优化问题时，易陷入局部最优。虽然粒子群算法在跳出局部最优解方面具有良好的特性，但是对于大规模优化问题的计算效率还需要改善[8]。此外，还有部分学者提出采用遗传算法和进化算法求解优化问题，但是遗传算法与进化算法受到适应性函数选择的影响[9]，并且对遗传机制的一些参数比较敏感，容易陷入局部最优解。梁静等人提出了一种改进粒子群优化 (ODPSO) 算法，在搜索前期和后期分别采用广义的反向学习策略和改进的变异交叉策略对当前种群的最优粒子进行更新[10]，从而提高种群的多样性，有利于获得全局最优解，该算法在处理约束的问题上还可以进一步完善。

人工神经网络主要应用于系统辨识、模式分类和自动控制等领域，Park首次采用Hopfield神经网络（HNN）求解电力系统的经济调度问题[11]，但是难以处理大规模系统优化问题。刘社民等人基于增广的Lagrange-Hopfield神经网络算法，提出了改进的增广Lagrange-Hopfield神经网络算法[12]，但是关键参数不能自适应调整。Lee应用增广的拉格朗日神经网络（ELANN）方法求解经济调度问题[13]，但是都有收敛速度较慢的不足。

本文基于增广的Lagrange Hopfield神经网络方法（ALHN），针对系统优化过程中参数不能自适应调整的问题，提出了基于ALHN的自适应神经网络算法。

1 含输电损耗电力系统经济调度问题

由于新能源的接入，发电机组分布范围广，由输电引起的损耗不容忽视，假设一个电力系统中含有台发电机组，它们通过输电网络与一条等效负荷母线相连，考虑输电损耗对功率需求的影响，计算各台发电机组的输出功率，使得该电力系统的发电总成本最小，因此，构成一个含输电损耗的电力系统的经济调度问题。其目标是在满足功率平衡约束和发电机功率约束的条件下使得发电总成本最小，成本函数如下：

其中，

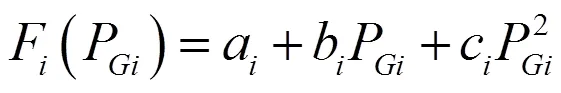
为了处理传输损耗，需满足功率平衡约束：

采用B系数法计算输电损耗，表达式如下：

每台发电机组的输出功率约束为：

考虑输电损耗的电力系统经济调度问题就是求解在满足上述约束条件下系统运行成本达到最小的系统运行方案。

2 基于ALHN的自适应神经网络算法

2.1 能量函数

增广Lagrange-Hopfield神经网络（ALHN）的能量函数是增广的Lagrange函数，其中的能量函数是通过Hopfield神经网络中的Hopfield关系项进行增广，从而克服了传统的Hopfield网络算法收敛速度慢的缺点。

经济调度问题的增广的Lagrange函数为：

引入NG个连续神经元和一个乘子神经元，能量函数表示如下：

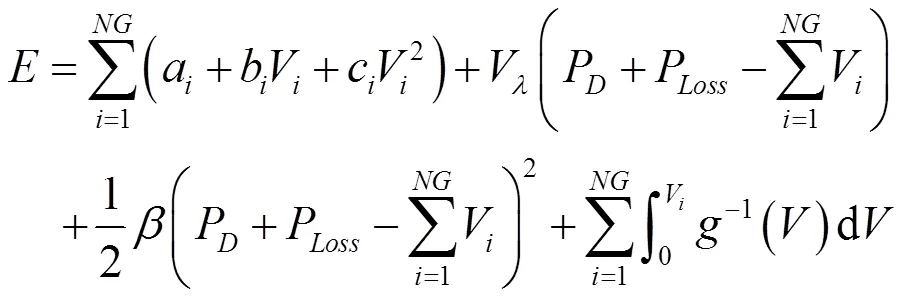
2.2 神经元更新的自适应算法

发电机组连续神经元的动态输入等于能量函数对神经元输出的负导数，即：

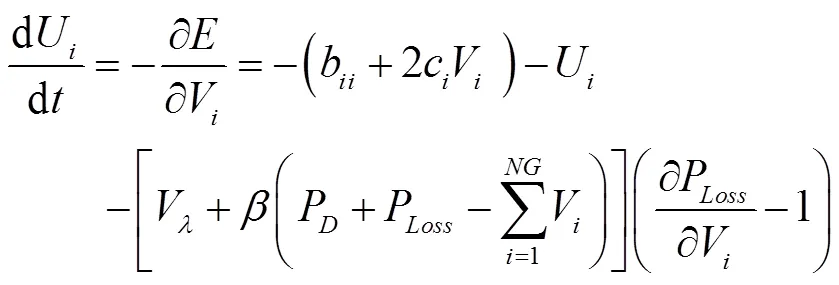
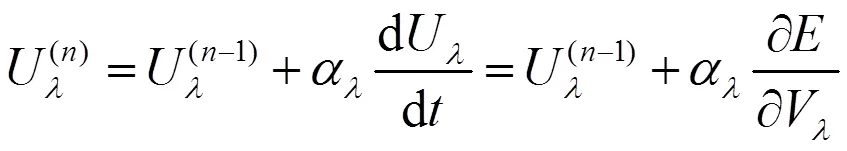
考虑传输损耗，引入功率平衡约束的误差：

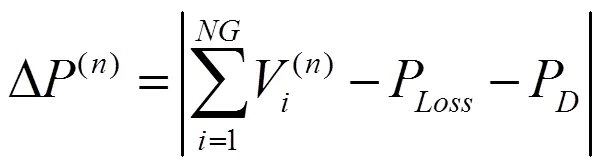
当解趋于最优解时，步长增加，可以提高收敛速度；当解背离最优解的时候，步长得到缩短，避免在错误的方向上偏离的更远。因此，式(10)至式(14)构成了连续神经元输入状态更新的自适应算法。下面对神经元的输出状态进行计算。

一般情况下，采用S型函数表示发电机组功率的连续神经元的输出函数：

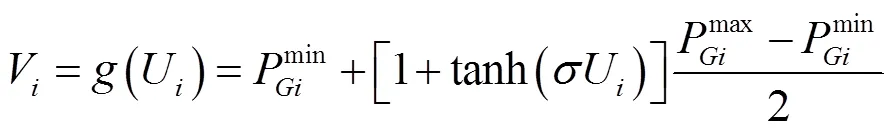
乘子神经元的输出函数如下：

综上所述，采用上述自适应步长更新算法，则构成了基于ALHN的自适应神经网络算法，可以根据功率平衡约束的满足程度，自适应调整步长，加速收敛速度。

3.3 收敛性证明

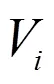
首先计算连续神经元状态的更新对能量函数的影响：

将式(15)带入上式，可得：

将式(8)带入上式，可得：

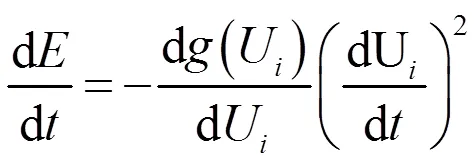
由于式(15)是增函数，因此d/d始终小于零，所以能量函数逐渐趋于极小值。

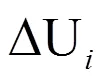
其次，计算乘子神经元状态的更新对能量函数的影响：

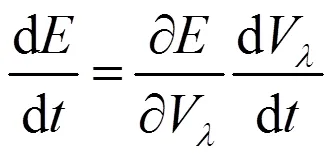
将式(16)带入上式，可得：

将式(9)带入上式，可得：

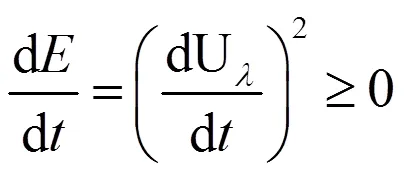
由证明可知，自适应更新算法并不会导致算法发散，并且对收敛速度有了很大改善，能够在迭代过程中，对约束条件进行实时评估，然后修改下一步的更新步长，改进了算法的收敛速度。

3 计算流程

3.1 参数选择及初始化

该算法首选需要确定设定神经元的初始状态，一般根据发电机组的容量按比例分配：

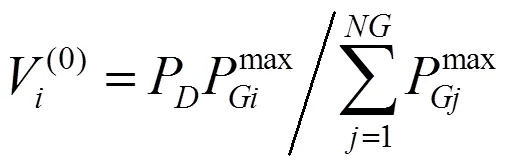
连续神经元的输入初始值如下：

3.2 结束条件

功率平衡约束误差由式(12)计算。第次迭代时神经元的迭代误差由下式计算：

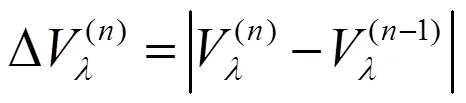
为了考虑以上三种误差，定义最大误差如下：

只有当最大误差小于预先给定的值或者达到最大迭代次数时，算法才会终止。

3.3 计算流程

基于改进ALHN的自适应神经网络算法，求解含传输损耗电力系统经济调度问题的计算流程如图1所示：

图1 计算流程图

4 算例

以三台发电机组构成的电力系统为例，发电机组的成本系数矩阵如下：

发电机组的运行极限约束如下：

输电损耗功率的相关参数：

算法参数选择如下：

为了进行比较，选取2=1.04，1分别取0.7、0.8、0.9时，以及1=2=1时的情形进行计算，最大误差如下图所示：

图1 最大误差曲线

通过自适应改变更新步长，可以大幅降低迭代次数，提高收敛速度。详细结果见下表：

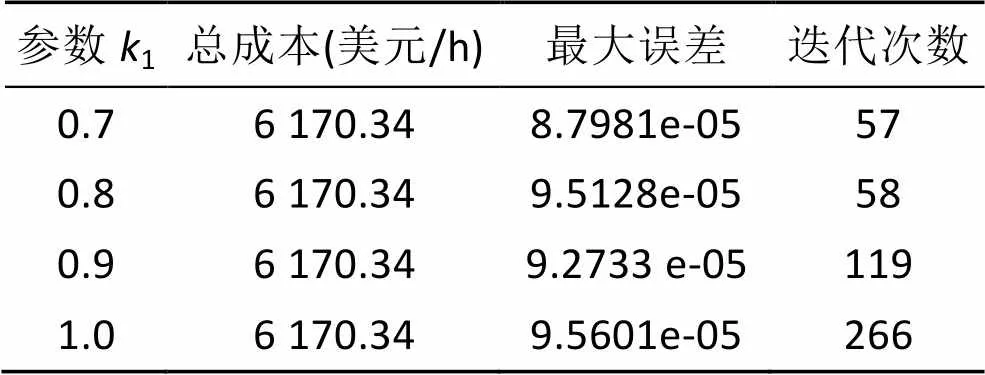
表1 计算结果对比

上述三种情况均求得最优解为：

则最低运行成本是6 170.34美元/h。

通过表1可知，当参数1=2=1时，即为ALHN的一般算法，迭代次数达到266次，其他情形为基于ALHN的自适应神经网络算法，迭代次数有了大幅降低，并且更新步长随功率平衡约束误差实时更新，计算结果说明本文算法具有更好的计算效率。

5 结论

本文基于Hopfield神经网络算法（ALHN）提出了一种自适应神经网络优化算法，提高算法的收敛速度。从理论上证明了算法的收敛性，可以提高能量函数趋于最小值的速率，为提高算法求解速度提供了理论基础。虽然本文算法在求解含有输电损耗的电力系统经济调度问题方向效果良好，但是在如何确定自适应参数方面还需要进一步从理论上完善。

：

[1] Al-Betar M A, Awadallah M A, Khader A T, et al. Economic load dispatch problems with valve-point loading using natural updated harmony search[J]. Neural Computing and Applications, 2018, 29(10): 767-781.

[2] 朱继忠, 余鹏飞, 禤培正等.计及风电和储能的综合经济调度方法[J]. 南方电网技术, 2017, 11(2): 2-7.

[3] 郑晓菁. 基于人工蜂群优化法的多区域电力系统经济调度 [J]. 计算机工程与科学, 2015, 37(8):1533-1539.

[4] 吴亮红, 王耀南, 袁小芳, 等. 基于快速自适应差分进化算法的电力系统经济负荷分配 [J]. 控制与决策, 2013, 28(4):557-562.

[5] 王凌, 黄付卓, 李灵坡. 基于混合双种群差分进化的电力系统经济负荷分配 [J]. 控制与决策, 2009, 24(8): 1156-1160

[6] Yousefi N. Solving nonconvex economic load dispatch problem using particle swarm optimization with time varying acceleration coefficients[J]. Complexity, 2016, 21(6): 299-308.

[7] Zou D, Li S , Wang G G , et al. An improved differential evolution algorithm for the economic load dispatch problems with or without valve-point effects[J]. Applied Energy, 2016, 181: 375-390.

[8] 郑恩让, 姜苏英. 基于改进粒子群优化算的分数阶PID控制[J]. 控制工程,2017,24(10): 2082-2087.

[9] 黄健, 周端. 基于改进差分进化算法的滑模控制参数整定[J]. 控制工程, 2018, 25(3): 484-487.

[10] 梁静, 葛士磊, 瞿博阳, 于坤杰．求解电力系统经济调度问题的改进粒子群优化算法[J/OL]．控制与决策.1-10.https://doi.org/10.13195/j.kzyjc.2018.1490.

[11] Park J H, Kim Y S, Eom I K, et al. Economic load dispatch for piecewise quadratic cost function using Hopfield neural network[J]. IEEE Transactions on Power Apparatus and System. 1993, 8(3): 1030-1038.

[12] 刘社民, 李建功, 裴付中, 等. 基于改进神经网络算法的电力系统经济调度[J]. 吉林大学学报(信息科学版), 2019, 37(1): 80-87.

[13] Lee S C, Kim Y H. An enhanced Lagrangian neural network for the ELD problems with piecewise quadratic cost functions and nonlinear constraints[J]. Electric Power Systems Research. 2002, 60(3): 167-177.

Cost-effective Dispatch of Power System Based on Adaptive Neural Network

Sun Yong

(Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)

TP731

A

1003-4862（2019）10-0006-05

2019-04-19

孙勇（1982-），男，高级工程师。研究方向：电源系统设计。E-mail: sunyong233@126.com