林业雇工劳动质量对农户营林技术效率的影响

贾代伟，沈月琴,2，朱 臻,2，黄晨鸣

（1.浙江农林大学 经济管理学院，浙江 杭州 311300；2.浙江省农民发展研究中心，浙江 杭州311300）

南方集体林区以丘陵为主的地形特征决定了林业生产过程中客观上存在着机械替代率低的问题。由于大量农村劳动力进入城市非农就业，林业经营主体需要通过雇佣劳动力以解决劳动力不足的问题［1］；日趋扩大的规模化经营对雇佣劳动力的依赖程度急剧增大，委托代理关系也应运而生。委托代理关系下的营林生产过程往往存在着信息不对称和 “道德风险”等问题，导致雇主对劳动过程的监督不到位［2］；而相对粗放的林业生产中，雇主无法准确观测劳动力的投入程度，雇工生产效率较低［3］。因此，在南方集体林区不断推进林业规模化经营的背景下，开展雇工劳动质量对农户营林技术效率的影响研究具有重要的理论和现实意义。国内外学者关于雇佣劳动对农林业生产影响的研究主要集中在农业领域。一种观点认为雇佣劳动对农业生产效率产生了负面影响。雇佣劳动存在 “道德风险”，雇佣劳动力的边际产出小于自有劳动力的边际产出，要保证劳动质量必须要付出大量的监督成本。有研究发现：存在雇工行为的家庭农业经营雇主，需要花费10%的劳动力时间来监督雇工，对劳动力在其他用途上的配置产生挤出效应。还有研究表明：团队组织内部监督不完备与激励不足，将会降低生产效率［4］。另一观点则认为雇佣劳动对农业生产效率有正向影响。张五常［5］认为分成制、定租制和混合制等委托-代理机制［3］是有效的。相比之下，目前针对林业雇工研究较少，从雇工视角探讨南方集体林区农户营林生产效率影响因素的研究还未见报道。本研究基于浙江省的实地调研数据，采用计量模型测算样本农户的营林技术效率，分析雇工劳动质量对农户营林技术效率的影响，以期为林业规模化经营中存在的雇工劳动问题提供决策依据。

1 雇工劳动质量对农户营林技术效率影响的理论机制分析

1.1 研究假说

根据委托-代理理论［3］，存在于雇佣劳动中 “道德风险”会导致雇佣劳动力的边际产出小于自有劳动力的边际产出；而相对粗放的林业生产管理会增加劳动力的监督难度，加重林业雇佣劳动中的机会主义行为。即营林生产过程中雇佣劳动会在一定程度上影响技术效率的提高。同时，雇工投入水平的差异对农户营林技术效率的影响也是不同的。雇工投入越多，则家庭自有劳动力越少，劳动监督难度越大，雇工劳动力的道德风险也越大，从而导致劳动生产质量下降，林业生产效率会因此受到影响（落入到生产可能性曲线内部）。就家庭自有劳动力与雇工关系而言，拥有剩余索取权的家庭自有劳动力更多地参与到营林生产中，则边际产出会随之升高，劳动质量会得到更大程度的保证，雇佣劳动对林业生产效率的负面影响程度也相对减弱。因此，可提出以下研究假说：农户营林生产过程中的雇佣劳动会对营林生产造成负面影响，且雇工劳动质量不同，雇佣劳动对农户营林技术效率的影响程度也不同。

1.2 理论模型

技术效率（technical efficiency,TE）是目前测度生产单位效率水平最常见的指标之一，一般用生产单位的实际产出与其理论上所能实现的最大潜在产出的比值来表示，本研究选用技术效率来衡量样本经营农户营林生产效率水平。用Yi表示第i个农户的林业产出，则随机前沿生产函数（stochastic frontier approach， SFA）可表示为：Yi=f（Xi， β）exp（Vi-Ui）。 其中：f（Xi， β）代表生产前沿面，Xi为生产要素的投入，本研究指资本、土地和劳动力的投入；（Vi-Ui）为混合误差，其中Vi表示随机误差，包含测度误差及不可控因素；Ui为技术效率损失，表示农户i的技术非效率项，服从独立的截断正态分布N（mi，δu2），其中mi为数学期望，δu2为方差。

技术无效率函数（mi）可设定为：其中：i表示第i位样本农户，Zji表示影响技术效率的各外生变量，δj为待估参数，反映各外生变量对技术效率的影响程度，μi为纯随机误差项。

在此基础上求解出技术效率水平：Ti=E（Yi∣Ui，Xij）/E（Yi∣Ui=0，Xij）=exp（-Ui）， 从而求解出平均技术效率：其中：n为农户数量，本研究采用最大似然估计法来估计前沿生产函数的参数。

2 数据来源、实证模型与变量选择

2.1 数据来源

本研究以浙江省南方集体林区为案例点，充分考虑地理位置、自然资源和社会经济发展差异，按农民人均可支配收入分层抽样选取浙江省建德市、开化县2个县（市）作为样本县（市）。2地农民人均可支配收入为23998和15736元，存在明显差异，反映出浙江省不同地区经济发展的差异性；森林覆盖率为76.2%和80.9%，均超出浙江省的平均水平，林业代表性较好。采取随机抽样法，在2个样本县（市）随机选取6个乡（镇），其中开化3个乡（镇），建德3个乡（镇）。为保证问卷的质量与信息的真实性，调查采取 “一对一”的访谈模式。共得到农户有效样本245户，其中有雇工参与的农户151户，无雇工参与的农户94户。

杉木Cunninghamia lanceolata是样本地区分布最广的树种之一，也是当地农户最主要的林业收入来源之一；因此，本研究以杉木为案例树种进行调研。调查内容包括农户家庭基本情况、林地基本情况、1个营林周期内最大地块上杉木的生产投入和产出情况等。样本分布见表1。

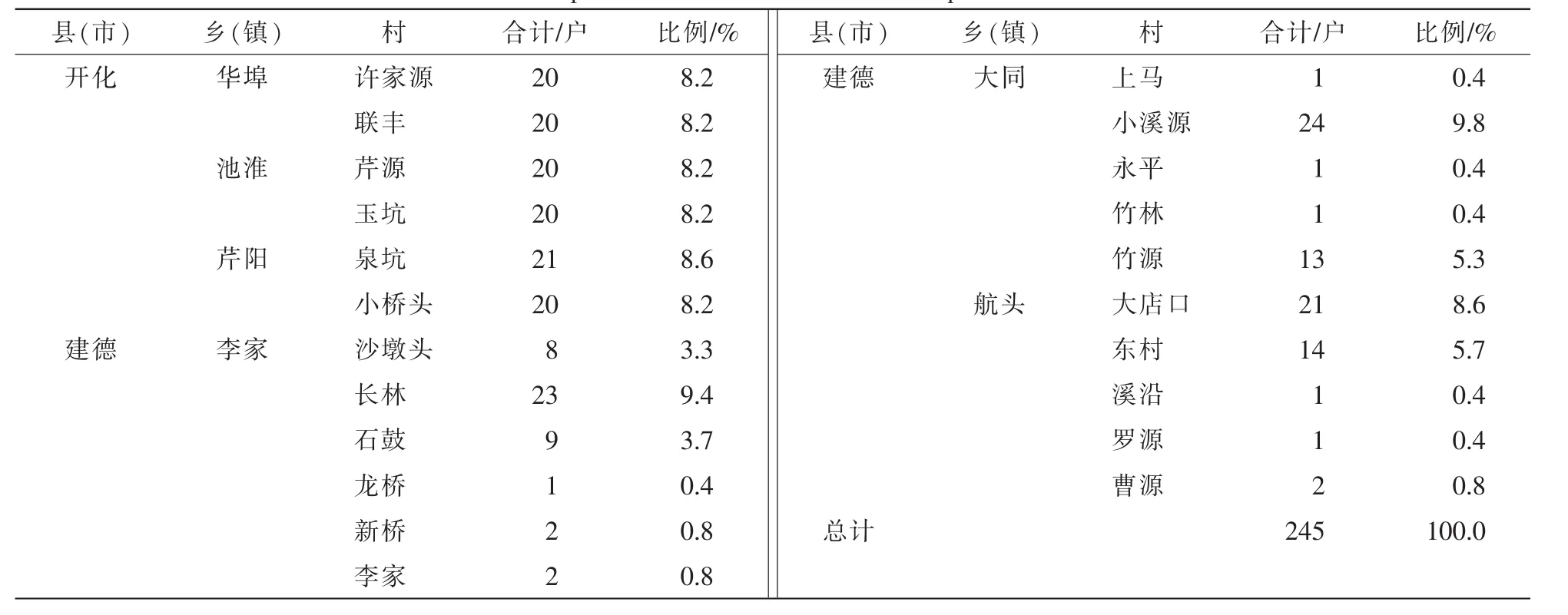
表1 农户有效样本分布情况Table 1 Specific distribution of effective sample of farmers

2.2 实证模型与变量选择

在测算林业技术效率之前，需要先确定前沿函数的具体形式，常见的前沿函数形式有C—D生产函数和超越对数生产函数。相对于前者，后者不仅形式灵活、易估计、包容性强，而且允许要素间替代弹性可变，没有对技术变化附加任何限制条件，因此近似性更好。考虑到南方集体林区农户拥有林地地块数量普遍较多，而农户林业生产中最重视且存更大雇佣劳动可能性的一般是最大地块，因此，本研究采用农户最大地块1个经营周期内的营林投入产出变量来构建生产函数。超越对数生产函数公式如下：lnYi=β0+β1lnKi+β2lnLi+β3lnMi+β4（lnKi）2+β5（lnLi）2+β6（lnMi）2+β7lnKilnLi+β8lnMilnMi+β9lnKilnMi+Vi-Ui。 其中：Y表示最大地块1个经营周期内的林业产出（主伐量）（m3）；K表示农户在最大地块的1个经营周期内所投入的费用（元）；L表示农户在最大地块的1个经营周期内所投入的劳动投工数量（工）；M表示最大地块面积（hm2）； β0～β9为待估参数。

通过对超越对数生产函数求导可以分别计算出各投入要素的产出弹性。资本投入要素的产出弹性为： η1=β1+2β4lnK+β7lnL+β9lnM。 劳动力投入要素的产出弹性为： η2=β2+2β5lnL+β7lnK+β8lnM。 土地投入要素的产出弹性为： η3=β3+2β6lnM+β8lnL+β9lnK。 农户技术无效率函数表示为：其中hj为关键变量，代表雇工劳动质量，表示农户最大地块1个经营周期内雇佣劳动力的投工质量情况，Zj为控制变量。

为全面测度营林雇工劳动质量问题，本研究构建了雇工年龄比例、雇工性别比例、雇工投工所占比例、受过技术培训的雇工所占比例等具体指标［6］作为关键变量。具体如下。①雇工年龄比例：40岁以下雇工所占比例（h1）、60岁以上雇工所占比例（h2）；②雇工性别比例：男雇工所占比例（h3）；③雇工投工所占比例：总投工中雇工所占比例（h4）；④受过技术培训的雇工所占比例（h5）。

一般研究将影响技术效率的地块特征、农业生产特征、户主特征等外生因素作为控制变量。①地块特征主要包括地块的地理位置（最大地块离家距离）、农户家庭山林总面积、农户家庭林地总块数、最大地块立地质量。地块离家距离越近，越便于林农对林地进行管理，所以，预期最大地块离家距离会对农户营林技术效率产生负向影响。农户家庭山林总面积越大、林地总块数越多意味着农户管理林地的难度也越大，平均到每个地块的管理时间就会越少，因此，预期其会对农户营林技术效率产生负向影响［7］。土地细碎不利于先进机械设备和技术的推广，控制病虫害难度加大，难以实现规模经营［8］，虽然也有研究表明耕地面积与生产率之间的反向关系［9］，但有些研究却表明此种关系并不显著［10］，因此预期其总效应不明确。地块的立地质量对效率的影响是显而易见的，肥沃的土壤相对于贫瘠的土壤更能提高农户的生产效率［11］，因此预期其会对农户营林技术效率会产生正向影响。②农业生产特征包括家庭务农人数、家庭总收入以及农户是否为补贴户。家庭务农人数会直接影响到劳动力要素的投入，因此预期其会对农户营林技术效率产生正向影响。农户家庭总收入的增加会加大农户的林业投资［12］，预期会对农户营林技术效率产生正向影响。农户若为补贴户，林业补贴的增加也会增加农户对林业的资本投入，因此假设其会对农户营林技术效率产生正向影响。③户主特征。包括户主年龄、户主的受教育年限、户主健康状况、户主是否担任过村干部。户主年龄对其技术效率的影响方向取决于该农户是更富有经验还是更守旧［13］；户主受教育年限越长，越能有效利用先进的农业生产技术［14］，因此，假设其会对农户营林技术效率产生正向影响。户主健康状况对农户营林技术效率的影响也是显而易见的：户主健康状况越好，越有利于家庭营林生产劳动和决策，因此假设其会对技术效率产生正向影响。干部身份一方面会带来收入效应，即干部获得先进生产技术和农业生产信息的渠道更多，这会对农户营林技术效率产生正效应；另一方面，干部身份同样存在替代效应，即干部用于家庭经营的时间更少，从事家庭经营的机会成本也较高，这会对农户营林技术效率产生负效应［15］。因此其具体影响尚不可知。具体控制变量如下：Z6表示农户是否为补贴户（0代表否，1代表是）；Z7表示户主是否为村干部（0代表否，1代表是）；Z8为农户家庭务农人数（人）；Z9为户主年龄（岁）；Z10为户主受教育年限（年）；Z11为户主健康状况（1代表好，2代表中，3代表差）；Z12表示农户家庭总收入（元）；Z13为农户家庭山林总面积（hm2）；Z14表示农户经营的山林总块数（块）；Z15表示农户经营山林中最大地块的立地质量（1代表好，2代表中，3代表差）；Z16表示最大地块离家的距离（km）。

3 结果与分析

3.1 描述性统计分析

由表2可知：样本农户最大地块整个营林周期内单位面积的平均产出为108.62 m3·hm-2，农户最大地块整个营林周期内单位面积的平均资本投入为8214.47元·hm-2，单位面积平均劳动力投入为375.23工·hm-2，平均林地投入为2.02 hm2。

表2 随机前沿生产函数模型变量的描述性统计Table 2 Descriptive statistics of variables in Stochastic Frontier Approach’s model

技术效率损失模型中（表3），户主的平均年龄为57.24岁，平均受教育年限为7.20 a，可以看出该地区的劳动力质量较差。88.00%的立地质量为中等及以上，最大地块离家距离平均为1.97 km，表明样本地区的立地质量和交通条件对林业经营相对有利。样本农户家庭户均地块为3.41块，表明样本地区林地细碎化问题并不严重。农户的家庭总收入均值为95501.74元，说明样本地区当地的经济条件利于林业发展。所有样本农户中仅有27.00%的农户为补贴户，说明国家的林补政策还未真正地惠及该地区。

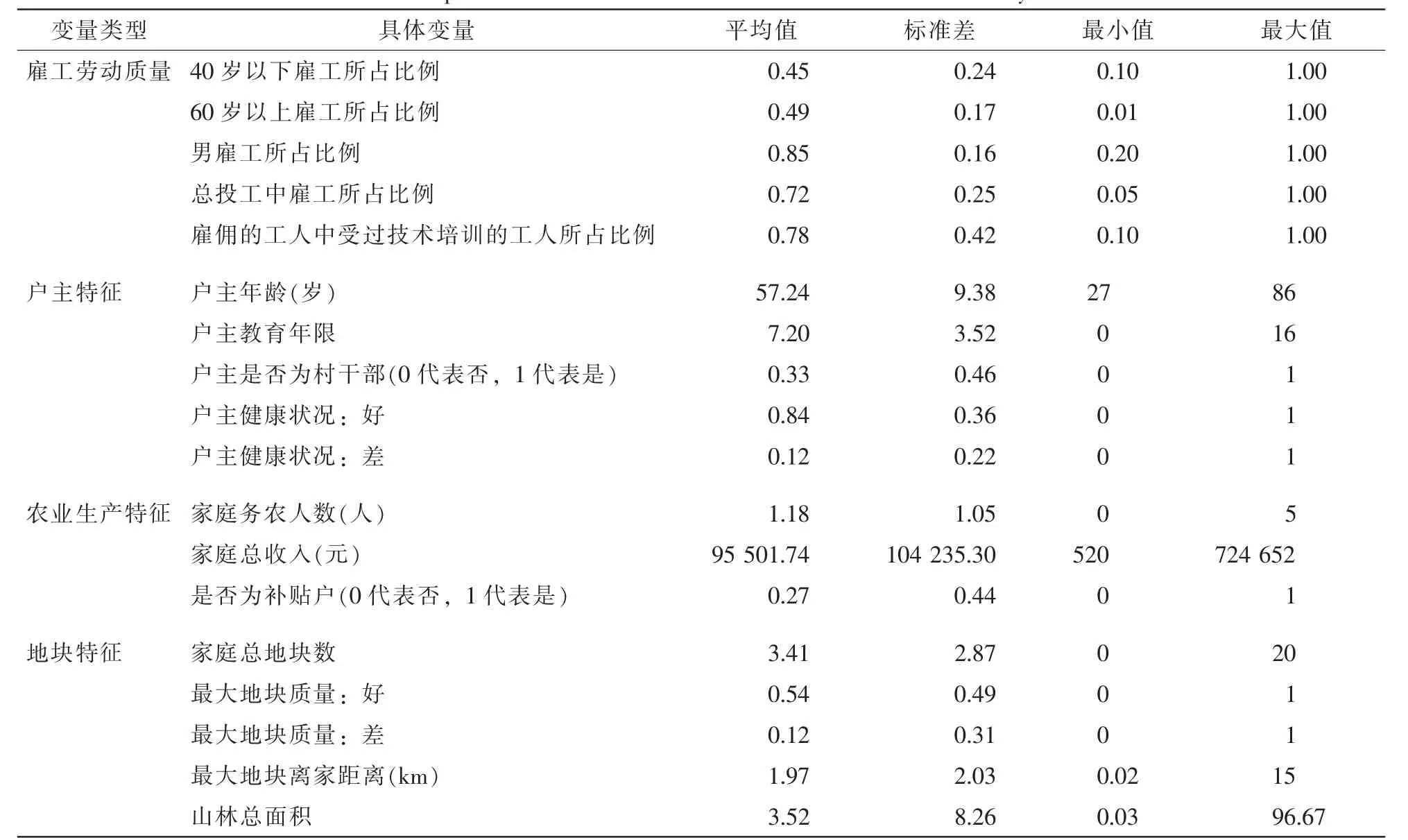
表3 技术效率损失模型变量的描述性统计Table 3 Descriptive statistics of variables in the loss of technical efficiency’s model

为消除因自变量之间多重共线性导致的模型估计结果偏差，在模型估计前对雇工质量各指标进行相关性检验。结果发现（表4）：雇工质量各指标之间不存在多重共线性问题，各指标可以作为自变量放入模型进行估计。

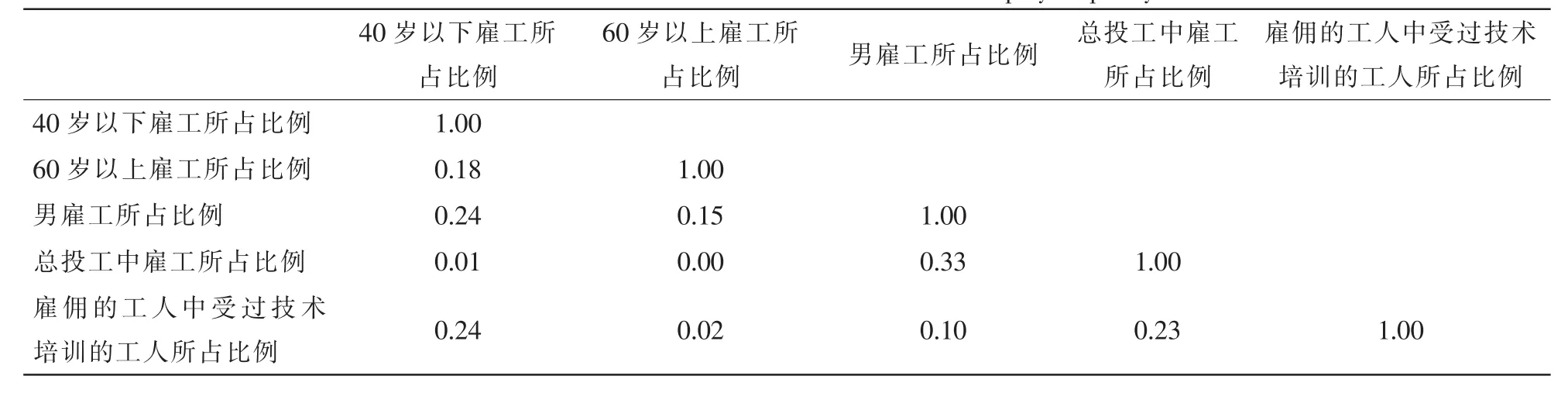
表4 雇工质量各指标系数相关矩阵Table 4 Relevance matrix of index coefficients of employee quality

3.2 实证结果分析

利用广义似然比（LR）检验可降低对SFA模型的依赖，避免函数形式的误设，从而从设定的待估计模型中筛选出最能拟合样本数据的模型。 LR 公式可表示为：RL=-2［lnL（H0）-lnL（H1）］ ～χ2（k）。 其中：L（H0）和L（H1）分别是零假设H0和备择假设H1下的似然函数值，表示受约束条件的自由度。将LR统计量与临界值进行比较，当LR统计量值大于临界值时拒绝原假设，否则，接受原假设。给出的2个零假设为：（1）规模户和非规模户的前沿面并没有显著的差异，即模型不需要添加是否为规模户的虚拟变量。（2）外生变量对技术效率无任何影响，即模型不需要添加外生变量影响因素。LR验证结果如表5所示。相对于基准模型，假设1在1%显著性水平上没有被拒绝，而假设2在1%显著性水平上拒绝原假设；说明原假设1对应的模型较好地拟合了样本数据，可作为本研究测度技术效率的主要模型。

3.2.1 随机前沿生产函数模型估计结果分析 表6为随机前沿生产函数模型的估计结果。将表6的回归系数代入上文生产投入要素产出弹性计算公式中可得到各投入要素的产出弹性。计算得：土地投入要素的产出弹性为2.25，说明样本地区林业生产对土地投入的依赖程度较高，即林业生产中最为稀缺的生产要素是土地，增加土地投入可以大幅度地提高林业产出。资本（-0.09）和劳动力（-0.23）投入要素的产出弹性均为负值，说明目前样本地区林业存在过度投入资本和劳动力的情况，单纯依靠增加林业劳动力和林业资本投入并不会带来林业产出的增加，相反还可能导致林业产出减少。

表5 假设检验结果Table 5 Hypothesis test results

表6 随机前沿生产函数模型估计结果Table 6 Estimated results of Stochastic Frontier Approach’s model

3.2.2 技术效率损失模型估计结果分析 在245份有效样本农户中，家庭最大地块1个营林周期内有雇佣劳动力的农户有151户，占总体样本的61.63%。总体农户平均技术效率值为0.57，有雇工农户平均技术效率值为0.59，无雇工农户的平均技术效率值为0.76。由表7可知：如果消除技术效率的损失，总体样本农户的平均技术效率还有43.00%的提升空间。由描述性统计结果可粗略看出无雇工农户的平均技术效率高于有雇工农户的平均技术效率，但雇佣劳动对农户技术效率的具体影响有待进一步计量分析。由样本农户雇工情况对农户营林技术效率损失影响的估计结果（表8）可知：在控制其他变量不变的情况下，雇工会对农户营林技术效率造成负面影响（P＜0.10）。雇工劳动质量指标中，总投工中雇工所占比例对农户的营林技术效率具有负向影响（P＜0.05）；原因可能是家庭自有劳动力和雇佣劳动力劳动质量存在异质性，雇主对劳动过程的监督很难到位，由此造成总投工中雇工所占比例越高，农户营林技术效率越低。户主年龄对农户的营林技术效率具有正向的影响（P＜0.10）；原因可能是随着户主年龄增大，其营林生产经验越丰富，对家庭营林生产越有利。户主良好的身体状况对农户营林生产技术效率具有正向影响（P＜0.05）；作为家庭最主要的林业劳动力和决策者，户主身体健康程度对林业生产至关重要。家庭总收入对农户营林生产技术效率具有正向影响（P＜0.05）；原因在于农户家庭总收入的增加会减少农户家庭林业生产的资金约束，农户林业投资概率会增大。山林总面积和家庭总地块数都对农户的营林技术效率具有负向影响（P＜0.10）；农户家庭山林总面积越大、家庭总地块数越多，农户管理林地的难度也越大，平均到每个地块的管理时间就会越少，农户无法对林地进行精细化地管理，影响了技术效率的提高。好的地块质量对农户营林生产技术效率具有负向影响（P＜0.10）；这与预期的影响方向相反，可能的原因是：农户会对质量较好的地块相对投入更少的肥料和劳动力等生产要素，因此使立地质量较优的地块产出情况反而不如立地质量较差的地块。

表7 样本农户营林技术效率总体情况Table 7 Overall situation of technical efficiency of sample farmers in forestry management

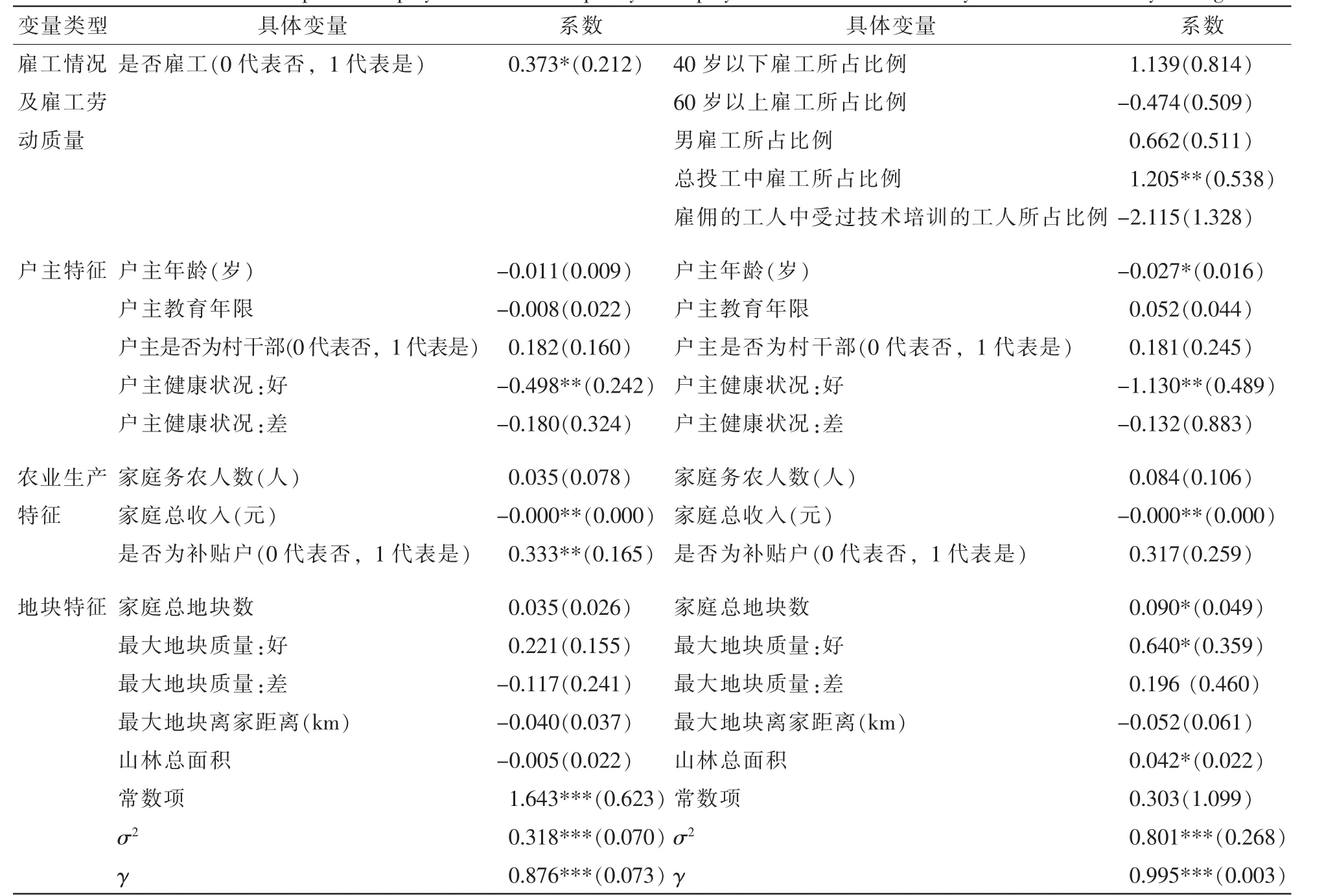
表8 雇工情况及雇工劳动质量对农户营林技术效率损失的影响估计结果Table 8 Estimation of the impact of employment and labor quality of employees on technical efficiency of farmers’forestry management

4 结论及建议

4.1 结论

本研究发现：样本农户的营林技术效率的平均值为0.57，表明样本农户在当前技术水平下平均56.60%的产出可以通过现有的生产要素组合来获得，样本农户的营林技术效率还有43.40%的提升空间。农户营林生产过程中的雇佣劳动确实会对营林生产造成负面影响，雇工劳动质量不同，对提高农户营林技术效率的影响程度不同；营林生产总投工中雇工所占比例越大，对提高农户营林技术效率的负面影响程度越大。

4.2 建议

建立有效的劳动监督和管理机制。雇佣劳动力在劳动过程中缺乏有效的劳动监督，雇工劳动质量低下，是营林生产技术效率下降的主要原因。因此，农户应根据雇工实际情况建立有效劳动监督机制，在劳动生产可计量的环节尝试使用绩效工资，并根据劳动成果给予一定的激励措施，减少雇工过程中 “搭便车”行为的发生，从而提高雇工劳动的质量。在目前林业规模经营日趋普遍的情况下，传统的生产经营和管理方式越来越难以适应，迫切需要建立高效的林业生产管理机制。革新传统林业管理理念，启用具有现代管理才能的人才管理林业经营；在林业生产的各个环节，制定科学合理的管理细则和林业生产流程。

推进适度规模经营，加大林业科技服务投入。解决各林业经营主体营林生产过程中的雇工劳动质量问题的关键是解决农村劳动力不足的问题。因此，推广林业机械化生产、开拓新型经营方式、积极推进林业适度规模经营均能在很大程度上解决上述问题。在地形条件较平缓的地区的林业规模经营户中可以依靠推进农业机械化替代劳动力，解决雇佣劳动所带来的劳动质量问题。同时，在机械替代较为困难的地区，可以尝试开拓林业服务外包、农户之间合作经营和托管经营等新型林业经营方式，促使劳动力要素配置更加专业化，也可以缓解由于雇佣劳动力所带来的劳动质量问题。对规模经营中出现的雇工劳动问题，需要进一步研究以寻找雇工劳动最优的比例，从劳动力层面对农户适度规模经营提出要求。