例谈数学在初中物理解题中的运用

(浙江省台州市白云中学,浙江 台州 318000)

物理是研究物质运动最一般规律和物质基本结构的学科，数学是研究现实世界中数量关系和空间形式的学科，数学是解决物理问题不可缺少的工具，本文通过典型例题探讨数学知识在初中物理解题中的运用。

1 平面几何知识的运用

初中物理中的力学、光学等问题经常涉及图形分析，因此数学的几何知识就派上了用场。

例1(2014年安徽中考):透镜的成像规律可以通过画光路图去理解，在光路图中透镜用图1(1)表示，O点为光心，F为焦点，图1(2)B′A′中是物体AB经透镜所成的像。

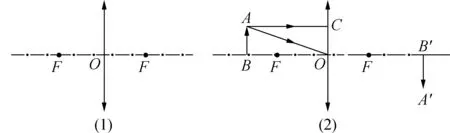
图1

(1) 请画出图1(2)中两条入射光线的出射光线，完成成像光路图；

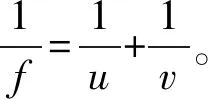
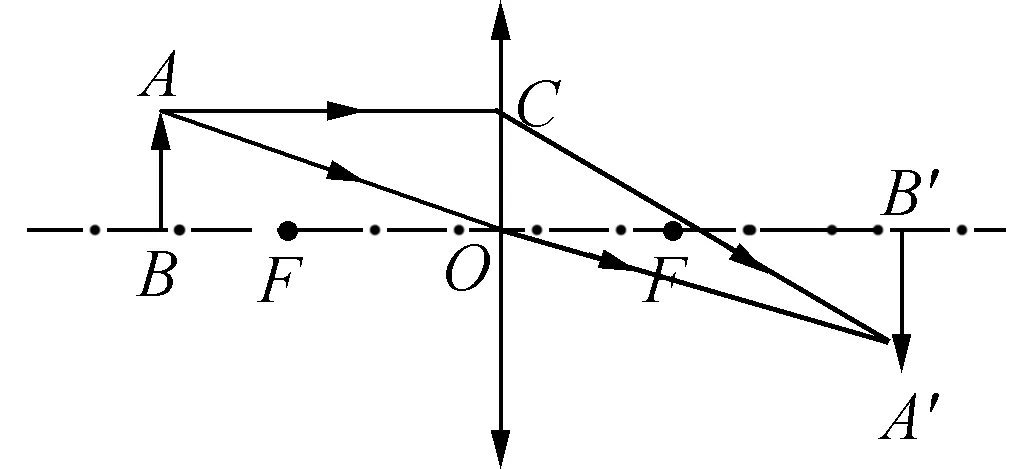
图2

解析：(1) 运用光学知识，画出如图2的光路图。

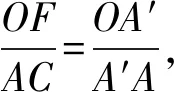
小结：本题的解答主要运用了三角形相似性质以及合分比性质等数学知识。

2 比例知识的运用

在初中物理中，经常会用到数学中的比例知识，特别在解决一些选择题或填空题时，合理运用合分比定理，能达到既准确又快速之效果。

例2:如图3所示，假设电源电压保持不变，当开关S接通a时，电流表A1和A2的示数之比为5∶7，而当开关接通b时，电流表A1和A2的示数之比为3∶4，则R2与R3的电阻之比为多少？

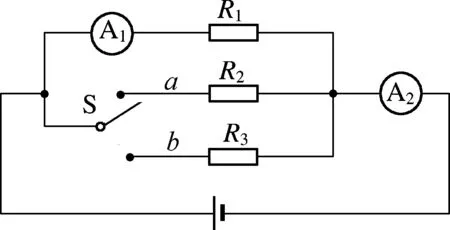
图3

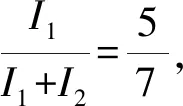
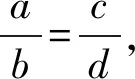
3 方程与不等式知识的运用

物理规律需要用数学形式表达出来，方程与不等式的知识是解决物理问题的“常规武器”。

例3：有一辆客车在平直的公路上行驶，公路前方有一座大山(公路穿过一条隧道)，汽车的行驶速度为20m/s，声音的传播速度为340m/s，当汽车鸣笛后，经过3秒听到了回声，请问汽车鸣笛时距离山多远？

解析：方法一：设汽车鸣笛时，与山的距离为s，由图4可知:2s-60m=3×340m,解得:s=540m。

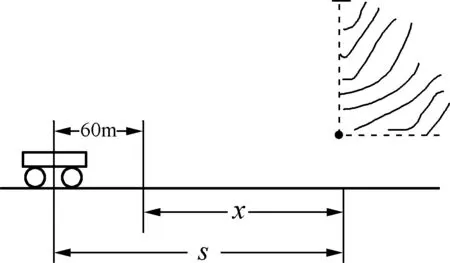
图4

方法二：设经过3秒后，车离山的距离为x，则2x+60m=3×340m，解得x=480m，故汽车鸣笛时距离山的距离s=480m+60m=540m。

小结：设未知量、通过已知条件、列方程求解是基本思路，由于未知量设法的多样性，一个问题可以有多种解法。

例4：如图5所示，电路的电源电压和灯泡电阻不变，R1=6Ω，灯L标有“6V，3.6W”字样，电流表量程为0～3A，滑动变阻器标有“3A”字样(电源电压8伏)。若电压表的量程为0～3V，电流表的量程为0～3A，只闭合S2时，在保证电路安全的情况下，求变阻器连入电路的电阻范围。

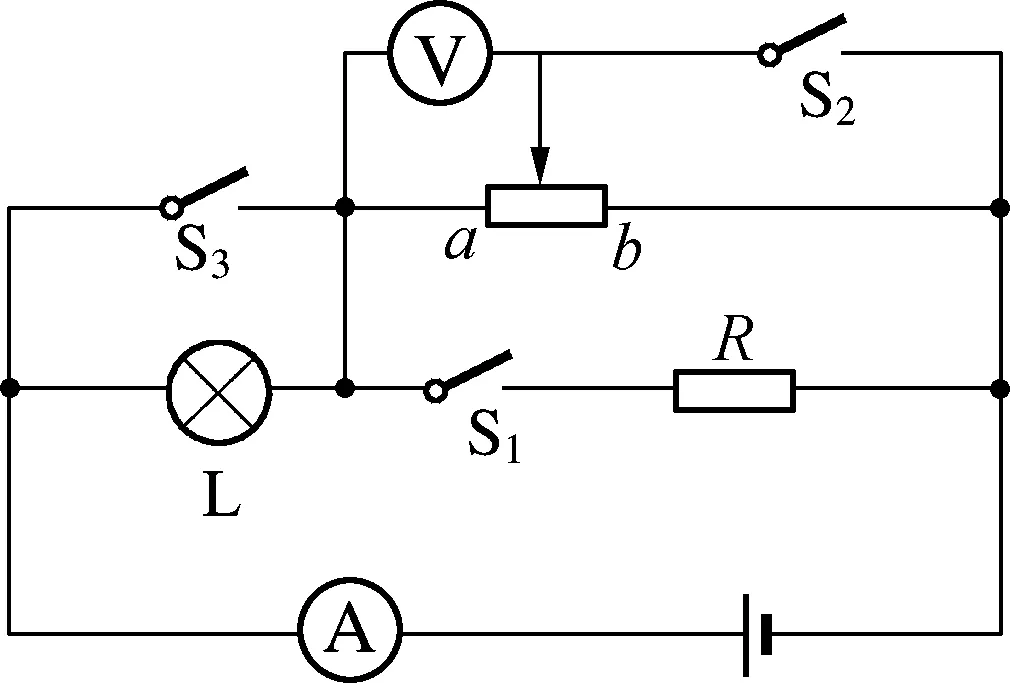
图5

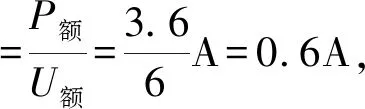
小结：由于物理量会受到实际条件的限制，使得这些量有变化范围的要求，而求解这些范围问题就要运用数学中不等式知识。

4 函数知识的运用

初中物理中有很多问题涉及正比例函数、反比例函数、一次函数、二次函数等有关数学知识。

例5：假设有一个滑动变阻器，其最大阻值为40Ω，将其与一个阻值为8Ω的定值电阻串联，外接电源电压为15V，求滑动变阻器的阻值为多大时，其功率最大？最大功率为多少？

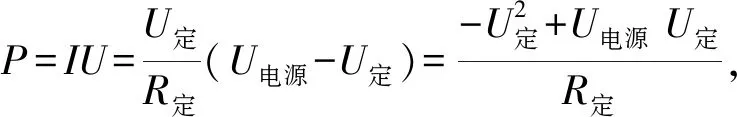
例6：如图6所示，一个体积为V的实心长方体，放入水中，静止时长方体浮在水面，水下部分的体积为V1，现将它露出水面的部分切除，再将剩余部分放入水中，若要求长方体剩余部分静止时，露出水面的体积V′与长方体的体积V的比值最大，则长方体的密度为多少？

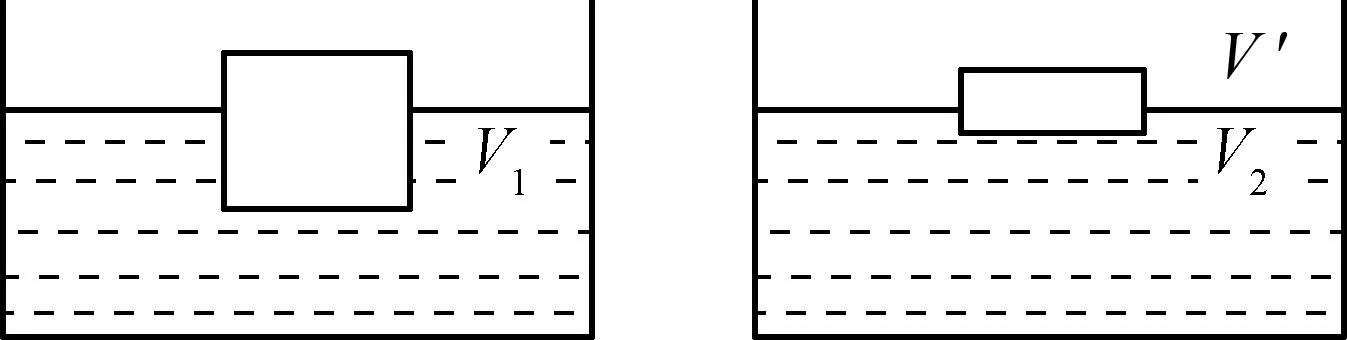
图6

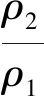
小结：在解决有关最值问题时，先转为数学中某个函数问题，然后利用函数的相关知识予以解决，在初中物理中，与最值有关的问题大多用二次函数解决。

数学方法在物理中的运用，需要教师平时在教学中有意识地引导学生，通过具体问题的解决及时进行总结、提炼，并加以巩固。