无人机三回路自动驾驶仪设计分析

盛启辉，赫荣光，赵志权，王小梅

（1.航空工业洪都；2.空装驻南昌地区军事代表室，江西 南昌，330024）

0 引言

无人机在飞行过程中，机体气动参数受高度、速度等飞行条件影响变化较大，而且机体通常都是严重欠阻尼的，有些甚至是不稳定的，抗扰动能力差，因此需要引入自动驾驶仪来加快弹体响应速度、改善阻尼、提高抗干扰能力，并精确、鲁棒地跟踪输入指令。

三回路驾驶仪是一种用速率陀螺和线加速度计反馈回路设计的自动驾驶仪，使用无人机姿态角速度、角度和加速度作为反馈信号。古典的频率域方法包括频率特性法和根轨迹法，可以设计出性能良好的三回路自动驾驶仪，但自动驾驶仪设计过多依靠设计者的经验，具有试凑性，设计过程较繁琐。因此，近十几年来利用现代控制理论设计自动驾驶仪的研究很多，应用最优控制理论设计的三回路自动驾驶仪，不仅从理论上分析了三回路自动驾驶仪的结构，同时还给出了三回路自动驾驶仪的性能指标，并实现了任意极点配置。

1 无人机俯仰通道运动状态空间方程

在无人机自动驾驶仪设计中，常选取姿态或者过载作为反馈量。俯仰通道过载方程可表示为[1]：

2 三回路自动驾驶仪的结构

利用线性二次型最优控制，可以得出三回路自动驾驶仪是“加速度指令与测量加速度误差与舵偏角速率的加权和”的最优解，具有良好的鲁棒性[3]。

线性二次型最优控制属于线性系统综合理论中最具重要性和最具典型性的一类优化型综合问题。线性二次型问题就是寻找一个容许控制量u*，是沿着由初态状态变量x0出发的响应状态轨迹x(t)，性能指标函数J(u*)取极小值。最优调节（LQR）问题的目标是综合最优控制量，在保证性能指标泛函取极小值的同时，使系统状态由初始状态量驱动到零平衡状态量。

对于线性时变受控系统，选取目标函数：

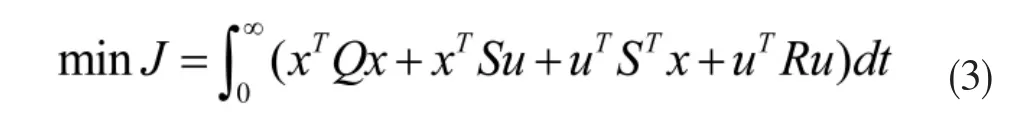
求解黎卡提方程，可得到最优控制律为

根据状态反馈矩阵与输出反馈矩阵之间的变换关系，可以得到输出反馈控制律。

对于单输入无限时间不变的LQR问题，最优调节系统至少具有如下稳定裕度[4]：

即系统至少具有6dB的幅值裕度和在两个方向上60°的相角裕度。

基于LQR设计的三回路驾驶仪分析如下：

对于线性时变受控系统(2)，选取目标函数：

求解黎卡提方程，可得到最优控制律为

对式（6）进行积分，可得到

式(7)是应用最优控制设计的三回路自动驾驶仪控制律。

3 三回路自动驾驶仪极点配置设计

式(7)给出了三回路自动驾驶仪的控制律，应用式(7)，可对三回路自动驾驶仪进行极点配置，图1给出了三回路自动驾驶仪的开环结构图。

根据式（2）和式（7）可推导出三回路自动驾驶仪的开环传递函数[3,5-6]：

其中

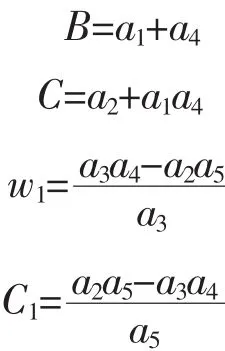
图1 三回路自动驾驶仪开环结构图

三回路自动驾驶仪的闭环传递函数：

理想三阶系统的极点配置形式通常是1个实极点与1对共轭极点，则有：

系统的期望极点与系统时域指标直接相关，可根据无人机飞行控制系统的性能指标要求进行选取，然后计算出KD、KI、Kϑ˙、Kϑ、Kac、Kδ。

4 三回路自动驾驶仪极点配置算例

应用式(8)、式(9)和式(10)计算三回路自动驾驶仪中的KD、KI、Kϑ˙、Kϑ、Kac、Kδ。

机体动力学系数：

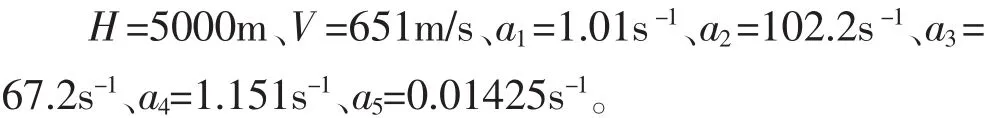
假设期望的驾驶仪开环截止频率和二阶环节的阻尼系数为：

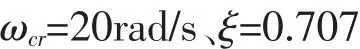
同时，令KD=Kac=Kδ。

选取三组期望极点，进行极点配置，计算回路的控制参数，比较三组极点配置后的自动驾驶仪的性能指标。

三组期望极点分别为：-9.2、-6.5±6.5j；-6.0、-9.0±9.0j和-14.0、-5.0±5.0j。 自动驾驶仪的闭环传递函数为：

设计结果及性能指标如表1所示,自动驾驶仪的闭环传递函数阶跃响应曲线如图2所示。

表1 三回路自动驾驶仪三组极点配置设计结果

图2 三回路自动驾驶仪阶跃响应曲线

从表1和图2可以看出，选取的第一组极点性能较好，自动驾驶仪的带宽最大，约1.0Hz，上升时间最小，约0.3s，相位裕度约为83.5°，阶跃响应超调量约1.4%。

通过分析可以发现，系统的闭环实极点对系统的响应速度影响较大，在第二组和第三组数据中，系统的闭环实极点与其它两个极点距离较远，对系统的响应速度影响较大，闭环实极点离虚轴越近，响应速度越慢，但是不会出现超调现象，而闭环实极点远离虚轴，响应速度较快，超调相对较大，但是超调量在10%以内。第一组数据的实极点位置在两个虚极点的左边，其幅值相等，系统性能指标介于第二组和第三组之间，具有最佳系统带宽。

5 结论

通过对三回路自动驾驶仪结构进行分析，并推导三回路自动驾驶仪的极点配置计算公式，应用三组期望极点数据对三回路自动驾驶仪进行极点配置，设计结果表明，第一组极点配置系统的性能较好，系统阶跃响应上升时间最小，带宽最大，相位裕度也较好，系统的性能指标较优。