改进复合权重TOPSIS法在船型综合评价中的应用
张明霞,姜哲伦,徐晓丽
(1. 大连理工大学 船舶工程学院,辽宁 大连116024;2. 中国船舶重工集团公司经济研究中心,北京 100120)
0 引 言
在船舶初步设计阶段,船舶主尺度和主要船型要素的选择通常具有多解性和不确定性,即在船型方案论证初期有多种可行的方案供选择。传统的船型方案主要采用母型船法建立,即根据以往建造的优秀船型来生成现有方案。该方法对油船、集装箱船等发展趋于完善的常规主流船型比较实用,但对于完井修井船等工程船来说,在技术经验不足的情况下,要求决策者能综合考虑船型的特点和工作要求,对现有同类型船进行多目标综合评价,通过排序并借鉴性能较优的船舶确定最优的新船方案。
在多目标评价中,选择合适的权重系数对于确保方案评价的准确性和科学性而言十分重要,目前普遍采用的赋权方法主要有主观赋权法[1]、客观赋权法[2]和组合赋权法[3]。主观赋权法是专家利用多年积累的经验得出各评价指标的相对重要程度,据此赋予其相应的比重,此法简单便捷、符合决策者主观意愿,缺点是未考虑评价对象自身的客观规律,计算结果具有一定的主观随意性;客观赋权法是通过对评价对象本身自带的信息进行分析,考察各评价指标的信息量,并以此为依据进行评价指标权重分配,该方法缺乏主观判断,所得评价结果易偏离实际;组合赋权法将主观赋权法与客观赋权法以一定方式组合,在一定程度上兼顾决策者的主观意愿和评价对象的客观信息,缺点是直接采用乘法合成的归一化法可能导致大者更大、小者更小的倍增效应[3]。
近年来,有很多学者对TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)法进行改进研究,例如:李想等[4]将邓氏与斜率灰色关联度法相结合,改进TOPSIS法;黄卫刚[5]对专家评分法、层次分析法(Analysis Hierarchy Process, AHP)、信息熵法和变异系数法等4种主客观赋权方法进行组合,改进TOPSIS法;黄胜等[6]构建了群体判断矩阵优化模型,将邓氏关联度引入TOPSIS法贴近度计算公式中;熊云峰等[7]将复合权重与 TOPSIS理论相结合建立船舶性能综合评价方法,对所有的评价指标,假设决策者以ξ的风险偏好倾向于用主观赋权法确定权重,以(1-ξ)的风险偏好倾向于用客观赋权法确定权重,但没有明确ξ的取值依据。本文基于上述研究,采用动态的改进复合权重计算方法[8]结合 TOPSIS[9]理论,根据第j个评价指标本身的情况确定对应的风险偏好jε;同时,通过将评价对象与正负理想解方案的接近程度相比较,并进行百分制转换[10],建立改进复合权重TOPSIS评价模型,对7艘修井船进行船型技术经济评价。
1 改进复合权重的获取
对于多目标综合评价问题,计算权重系数是至关重要的。通常将权重计算方法分为侧重于决策者主观意愿的主观赋权法(如AHP、专家评价法等)和客观赋权法(如熵权法(Entropy Weight Method, EWM)、因子分析法等)2类[11]。为兼顾主观意愿和客观事实,本文以动态方式将AHP与EWM相结合,构成满足要求的复合权重。
假设某评价问题有m个评价对象和n个评价指标,采用AHP确定的第j个指标的权重为jω,采用 EWM确定的第j个指标的权重为jθ;同时,假设决策者以jε的风险偏好倾向于采用AHP确定的权重,以(1-jε)的风险偏好倾向于采用EWM确定的权重。
1.1 AHP权重系数的获取
AHP按性质将与决策有关的因素从高到低分成目标层、准则层和方案层,利用下级层次对上级层次各指标的相对重要性确定指标权重,具体步骤如下。
1.1.1 明确比较标度
AHP采用指标间两两比较的原理对同层次的相关指标进行赋值比较,本文采用1-9标度法。表1为指标重要程度分级比较标准,若元素ak与aj相比得到akj,则aj与ak相比得到的标度为ajk=1/akj。

表1 指标重要程度分级比较标准
1.1.2 构造判断矩阵
设比较得出的判断矩阵为A={ajk|k,j=1,2,…,n},有

通常,判断矩阵的特征值和特征向量的计算相对复杂,可采用简化方法计算其近似值,例如方根法,首先将判断矩阵的列向量归一化,接着近似求出对应的最大特征值λmax和对应的特征向量F,最后将F归一化,确定各评价因素的权重,计算式[12]为

1.1.3 一致性检验和权重向量
为检验判断矩阵中各元素的协调性,需进行一致性检验,通常可表示为

式(5)中:n为评价指标的数量值;CR为一致性检验指标;RI为平均随机一致性指标,其取值与比较因子的数量有关(见表2)。通常认为:当时,判断矩阵满足一致性要求,权重向量当时,判断矩阵不满足一致性要求,必须重新对其进行调整,直至符合一致性要求为止。

表2 随机一致性指标RI的数值
1.2 EWM权重系数的获取
EWM[7]是一种根据决策矩阵数据的特点得到的客观赋权法,充分利用决策矩阵的结构信息分析得出各目标的权重系数,适用于评价对象间相关性很小或不相关的情况。
根据决策矩阵B计算熵Ej,有


定义fj为各方案在第j个评价指标下贡献度的一致性程度,有

因此,第j个评价指标标准化的EWM权重系数为

由此可看出,当各方案在某个评价指标下的数值趋于一致时,fj趋于0,表明各方案对于该评价指标而言基本无差异,该评价指标对方案的评价贡献度的影响较小,该评价指标的权重系数值较小;当各方案在某个评价指标下的数值相差较大时,fj趋于1,表明该评价指标对方案的评价贡献度的影响较大,该评价指标的权重系数值较大。
1.3 改进复合权重计算
为将采用主观赋权法和客观赋权法得到的权重有机结合起来,考虑到不同指标值的分散程度不同,采用固定的权重偏好系数无法充分体现EWM的信息特点,以距离指标jρ作为复合权重得到最终的指标权重。
结合已求出的AHP权重系数jω和EWM权重系数jθ,复合权重可表示为

为确定jε的值,可用最小二乘法建立规划模型,有

通过求解可得动态的权重偏好系数jε为

2 建立改进复合权重TOPSIS综合评判模型
TOPSIS的基本原理是借助多目标决策问题中正理想解与负理想解的相对距离对待评价方案进行排序。正理想解通常是虚构出来的最佳方案,其每个指标都取为待评价方案中的最优值;负理想解的指标是待评价方案中的最劣值。TOPSIS通过考量方案对正理想解和负理想解的趋近程度来对方案进行综合排序。显然,方案越趋近正理想解越优。
2.1 初始判断矩阵

2.2 决策矩阵标准化
在评价指标中,将数值越大越优的指标归为收益性指标,将数值越小越优的指标归为消耗性指标。为使评价指标间具有一致的可比性,应对决策矩阵进行标准化处理,具体步骤如下。
1) 对评价指标进行无量纲处理
(1) 对于收益性指标,有

(2) 对于消耗性指标,有

2) 对评价指标进行归一化处理,有

最终得到的标准化决策矩阵为
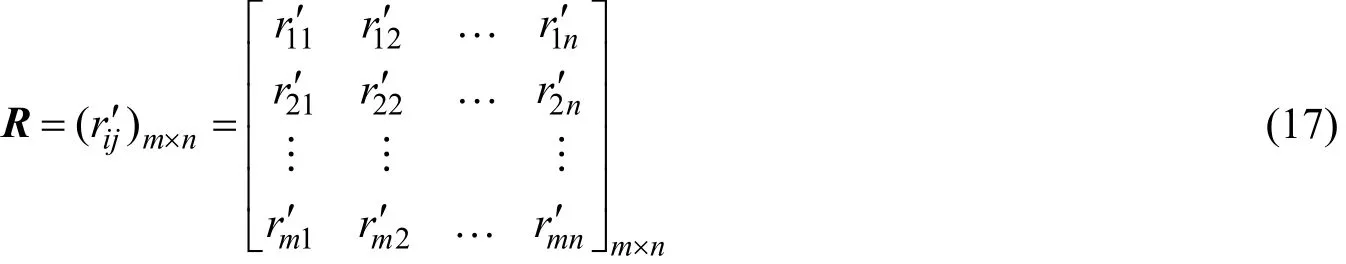
2.3 贴近度分析
由于在决策矩阵标准化过程中收益性指标和消耗性指标的评价标准已修正一致,即指标值越大越优,因此正理想解为决策矩阵R中各行向量的最大值构成的方案,负理想解取决策矩阵R中各行向量的最小值,表达式为

式(18)中:R+和R-分别为正理想解和负理想解。
由此,各评价方案与正理想解和负理想解的距离分别表示为

式(19)中:和分别为第i个方案与正理想解和负理想解的距离值;jε为上文求得的复合权重值;和分别为R+和R-相对应的指标值。
由此,贴近度ci的计算式可表示为

显然,待评价方案的贴近度取值为(0,1),越接近于1说明其距离负理想解越远,方案越优。
3 船型方案评价实例
3.1 船型算例
本文以7艘修井作业船为例进行分析,由于修井船方案涉及的因素错综复杂,需综合考虑实际的市场需求、技术经济性、船东的偏好和目前的绿色环保要求等各方面的因素,因此对其进行评价是一个多准则、多目标的决策问题。通过分析确定影响该船型作业性能和技术水平的主要因素有空船重量、船长、最大钩载、甲板可变载荷、主机功率、载重量和最大作业水深等,其他需考虑的因素为经济性和绿色度,因此建立的评价指标体系包含最大钩载系数(RH)、作业水深系数(RDW)、可变载荷系数(RF)、单位进尺油耗(RQ)、海军部系数(RE)和船舶能效设计指数(Energy Efficiency Design Index, EEDI)等6个评价指标,各项指标的计算式见表3,相应的各项指标初始数据见表4。
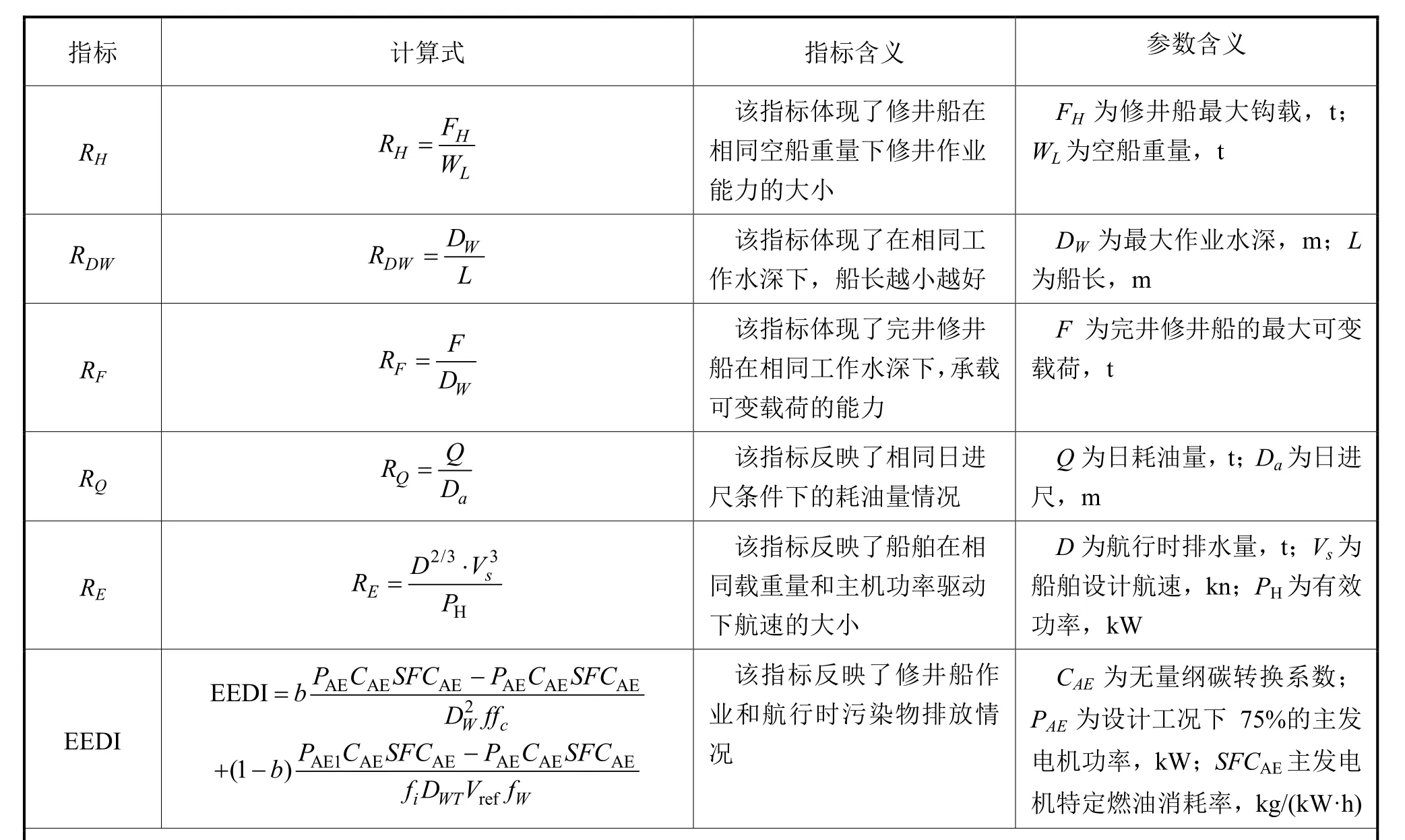
表3 完井修井船各项指标的计算式

表4 7艘修井船各项指标初始数据
RH、RDW、RF和RE属于效益性指标,其值越大方案越优;RQ和EEDI属于消耗性指标,其值越小方案越优。
用第2.2节中的方法建立标准化决策矩阵R,有

3.2 复合权重计算
3.2.1 AHP权重计算
综合考虑完井修井船的技术性、经济性和绿色度,定义RH、RDW、RF和RQ为主要指标,RE和EEDI为次要指标,建立以下6组评价指标重要度排序序列:
以第1组为例,生成判断矩阵A为

由式(22)计算得到:λmax(A)=6.1565,CI=0.0313,RI=1.2400,CR1=0.0252 <0.1000,认为判断矩阵A通过一致性检验。利用式(2)和式(3)计算AHP权重向量W=(RH,RDW,RF,RQ,RE,EEDI),有:ωa=(0.1559,0.2923,0.2923,0.1559,0.0741,0.0295);ωb=(0.2923,0.1559,0.2923,0.1559,0.0741,0.0295);ωc=(0.2923,0.2923,0.1559,0.1559,0.0741,0.0295);ωd=(0.1559,0.2923,0.2923,0.1559,0.0295,0.0741);ωe=(0.2923,0.1559,0.2923,0.1559,0.0295,0.0741);ωf=(0.2923,0.2923,0.1559,0.1559,0.0295,0.0741)。
3.2.2 EWM权重计算
利用式(6)~式(9)计算 EWM 权重向量θ=(0.120,0.196,0.140,0.206,0.135,0.203)。
3.2.3 复合权重计算
利用式(10)~式(12)计算得到的复合权重ρ=(RH,RDW,RF,RQ,RE,EEDI)为:aρ=(0.1575,0.2700,0.2101,0.2063,0.1077,0.0484);ρb=(0.1916,0.2111,0.2192,0.2152,0.1123,0.0506);ρc=(0.1857,0.2729,0.1750,0.2086,0.1088,0.0490);ρd=(0.1563,0.2681,0.2086,0.2049,0.0475,0.1146);ρe=(0.1902,0.2096,0.2175,0.2136,0.0495,0.1196);ρf=(0.1843,0.2709,0.1738,0.2071,0.0480,0.1159)。
3.3 船型评价
选择标准化决策矩阵R各行向量的最大值作为正理想解R+,各行向量的最小值作为负理想解R-,分别为:R+={ 0.228,0.193,0.293,0.143,0.295,0.161};R-={ 0.029,0.110,0.074,0.143,0.053,0.117}。
利用式(19)~式(21),采用改进复合权重(ICW)作为赋权法的ICW-TOPSIS法计算得到的待评价船舶得分情况见表5。
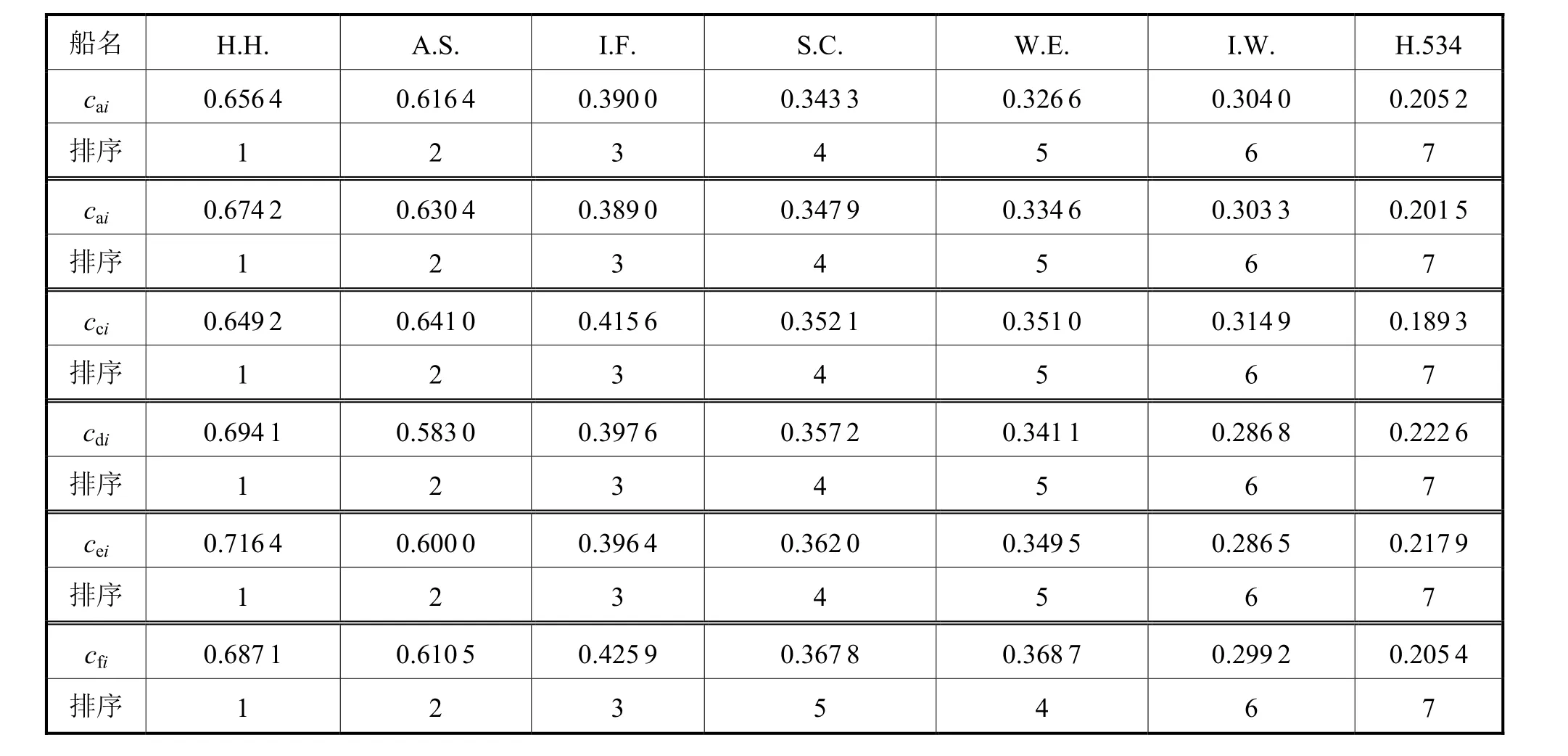
表5 ICW-TOPSIS法评价结果
仅采用AHP作为赋权法的AHP-TOPSIS法计算得到待评价船舶得分情况见表6。

表6 AHP-TOPSIS法评价结果
仅采用EMW作为赋权法的EMW-TOPSIS计算得到的待评价船舶得分情况见表7。

表7 EMW-TOPSIS法评价结果
3.4 结果分析
图1和图2分别为不同权重下ICW-TOPSIS法和AHP-TOPSIS法分别与EMW-TOPSIS法的待评价船舶评价结果对比。

图1 ICW-TOPSIS法与EWM-TOPSIS法评价结果对比

图2 AHP-TOPSIS法与EWM-TOPSIS法评价结果对比
1) 从图1和图2中可看出,当采用不同的赋权法时,评价方案的得分排序有差别。例如,对于H.H.和A.S.来说:当采用ICW-TOPSIS法和AHP-TOPSIS法计算时,H.H.的得分优于A.S.;当采用EW-TOPSIS法计算时,A.S.的得分优于H.H.。这说明在考虑主观意愿的情况下,H.H.主观上比较重视的某些评价指标较优,因此能在综合评价中超过A.S.。
2) 采用ICW-TOPSIS法计算所得结果受主观意愿改变的影响较小,采用AHP-TOPSIS法计算所得结果受主观意愿改变的影响较大。从图1和图2中可看出,当主观意愿发生改变时,ICW-TOPSIS法的6条评价曲线较为集中,而AHP-TOPSIS法的6条评价曲线较为分散。
4 结 语
对于决策者来说,船舶性能评价的关键在于所采用评价方法的科学性和准确性,与传统的评价方法相比,本文提出的改进复合权重TOPSIS船型评价模型将主观赋权法与客观赋权法相结合,充分体现决策者的主观意愿和评价指标值的客观信息。算例验证结果表明,该评价模型适于船型方案多目标综合评价,与现有的方法相比具有以下特点:
1) 采用改进复合权重TOPSIS评价模型很好地完成了算例中7艘修井船的评价,该模型具有计算原理简单的特点,较易推广应用到更多评价指标、更多评价对象的评价问题的求解中,适于评价对象较多且待评价船型的性能参差不齐的情况。
2) 改进复合权重TOPSIS评价模型是一种直观、合理的多目标决策模型,适用于船型方案优选评价。该模型受主观意愿与评价指标集客观信息的复合影响,对主观意愿的敏感度较弱,能有效避免决策者经验不足导致的主观权重选择出现偏差的问题,除了能用于技术成熟的常规船型的评价以外,还适用于具有某些特种功能的船舶(这类船舶根据不同的工作需要设计的侧重点不同,具有可选的参考船型数量少、主观性强等特点)。
3) 改进复合权重采用动态风险偏好εj,将主观赋权法与客观赋权法相结合,与文献[4]提出的方法相比,根据得出的主观权重值和客观权重值自身的信息,能比较客观地实现决策者的主观意愿与评价指标值客观信息的结合,提高评价模型计算的准确性。

