基于板壳模型的减摇鳍鳍翼水力负荷结构分析

魏建庆，操安喜，金永兴，付崇博

（1. 上海复合材料科技有限公司，上海 201112；2. 上海海事大学，a. 海洋科学与工程学院；b. 商船学院；上海 201306）

0 引 言

减摇鳍是用来减小船体横摇的装置，通常安装于船中两舷舭部。通过操纵机构转动减摇鳍，使其与水流产生相互作用，从而形成横摇力矩，减小船体横摇。目前减摇鳍在船舶减摇装置中仍占主导地位，超大型、精密型和智能型的船舶减摇装置可能是未来一段时期内的研究热点[1]。随着研究的不断深入，收放式、嵌套式减摇鳍相继被设计出来，其中：收放式减摇鳍能根据实际需要灵活使用；嵌套式鳍翼相比整体式鳍翼，能大大减小鳍箱开口[2]。收放式减摇鳍涉及转鳍机构和收放鳍机构，可采用 PATRAN/NASTRAN软件对其进行三维非线性接触有限元计算，确定其应力应变场，从而为其优化和改进提供设计依据[3]。就减摇鳍本身而言，可使用MSC.NASTRAN软件对其进行强度校核和应力分析[4]。减摇鳍不是孤立的结构，必须将其装配到船体上；对于减摇鳍与船体的适配性，可单独在敞水条件下使用 FLUENT软件进行分析研究，测试其减摇效果[5]。国内已有专家[6]对减摇鳍的实体模型进行水动力分析，但未涉及板壳模型方面的研究。

随着船舶逐步朝大型化方向发展，减摇鳍会越来越大，对相关机构的要求会越来越高，使用实体模型分析所耗费的建模时间和计算时间会越来越长，计算误差也会越来越大。为了探讨板壳模型与实体模型在减摇鳍仿真方面的不同，获得更好的计算方法，本文直接在WORKBENCH软件中以NACA64型减摇鳍为蓝本，建立鳍翼的板壳模型和实体模型，分别采用这2种模型进行水动力负荷结构分析，获得相应的参数。

1 流固分析的理论基础

1.1 流体控制方程

流体流动要遵循物理守恒定律，基本的守恒定律包括质量守恒定律、动量守恒定律和能量守恒定律。对于一般的可压缩牛顿流而言，守恒定律通过以下控制方程描述。

1) 质量守恒定律描述为

2) 动量守恒定律描述为

式(1)和式(2)中：t为时间；ff为体积力矢量；ρf为流体密度；v为流体速度矢量；τf为剪切力张量。τf可表示为：

式(3)中：p为流体压力；μ为动力黏度；e为速度应力张量。

1.2 固体控制方程

固体部分的守恒方程可由牛顿第二定律导出，即

式(5)中：ρs为固体密度；σs为柯西应力张量；fs为体积力矢量；为固体域当地加速度矢量。

1.3 流固分析方程

流固分析遵循最基本的守恒原则，因此在流固分析交界面处应满足流体和固体应力τ、位移d、热流量q及温度T等变量相等或守恒，即满足

式(6)～式(9)中：fτ，df，qf和Tf分别为流体中的应力、位移、热通量和温度；sτ，ds，qs和Ts分别为固体中的应力、位移、热通量和温度。

2 鳍翼水动力计算

2.1 流场及鳍翼几何模型

采用 WORKBENCH软件建立板壳模型和实体模型，减摇鳍的型线图参考中船重工第 704研究所的《NACA64型9m2后鳍型线图》得到，其主要特征参数见表1。

表1 减摇鳍主要特征参数

该减摇鳍为非对称型，其几何模型见图1。为了减少回流，选取类长方体流场（见图2），流场边界长方体的长度取约30L，流场宽为10L，流场高为20L，L为平均弦长2739mm。

2.2 流场和鳍翼网格划分

采用ANSYS网格生成软件划分鳍翼的计算流体动力学（Computational Fluid Dynamics, CFD）计算网格。采用在鳍翼近壁面建立膨胀层的方式生成四面体网格。在MESHING软件中将网格精度调为最高，鳍翼表面的膨胀层设置为40层，以保证在近壁面生成足够的网格数量。网格总数约为3314177万个，网格划分后的效果见图3。

图1 减摇鳍几何模型

图2 流域流场

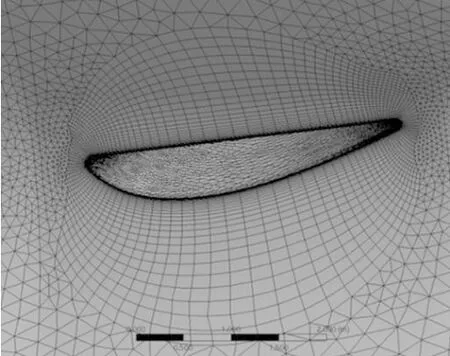
图3 网格划分后的效果

2.3 流场中的计算

设置鳍翼升力系数和阻力系数观测曲线，经约3000次迭代计算，升力和阻力的变化逐渐趋于稳定，变化幅度收窄，接近于一条直线，此时认为迭代计算收敛。28°攻角下的升力系数曲线和鳍翼处流线分别见图4和图5。

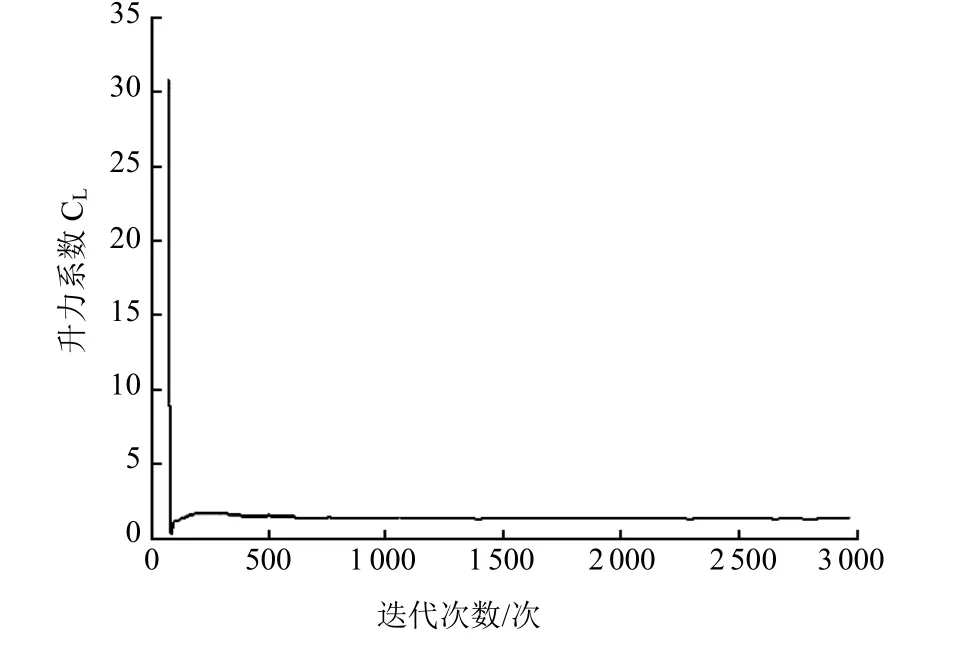
图4 28°攻角下的升力系数曲线

图5 鳍翼处流线

3 鳍翼结构有限元模型计算

3.1 鳍翼结构的有限元模型

本文所述减摇鳍模型是在WORKBENCH软件中通过板壳建立的，因此需分别对各板壳的厚度定义，而在建立实体模型时需建立厚度与之相同的实体。

由模型型线图可知，减摇鳍外壳板厚度为10mm，弦向板厚度为10mm，展向板厚度为14mm，减摇鳍与船体相连的部分板壳厚度为14mm。

实体模型（见图 6）和板壳模型（见图 7）在外观上没有显著不同，唯一的不同点在于实体模型中显示出了各骨架的厚度。实体模型和板壳模型局部模型分别见图8和图9。

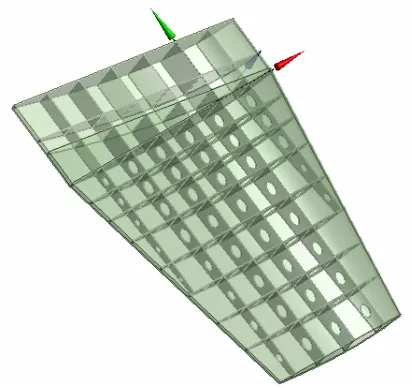
图6 实体模型

图7 板壳模型

图8 实体模型局部模型

图9 板壳模型局部模型

3.2 结构模型网格

板壳模型中网格边长设定为50mm，板单元以四边形为主，在形状变化较大的位置辅以三角形单元，网格总数为20581个，节点数为20035个；实体模型总网格数为117600个，节点数为227800个。图10和图11分别为实体模型网格和板壳模型网格。

图10 实体模型网格

图11 板壳模型网格

由减摇鳍2种模型各数据对比（见表2）可很明显地看到，板壳模型相比实体模型，节点和网格少很多。

表2 减摇鳍实体模型与板壳模型网格数据对比

3.3 水动力导入

减摇鳍表面载荷由CFD计算获取，利用ANSYS/WORKBENCH软件提供的载荷传递接口，可方便地将减摇鳍表面压力映射到板壳结构和实体结构的有限元模型上，最后施加到减摇鳍的表面，分别进行计算比较。由于2种模型的一致性，导入力情况基本相同，都在98%左右。图12为载荷传递情况，图13为鳍翼载荷加载情况。

图12 载荷传递情况

图13 鳍翼载荷加载情况

4 计算结果

4.1 结构应力

实体模型的等效应力云图和板壳模型的等效应力云图分别见图14和图15。由数值计算结果可知，板壳模型的最大等效应力为161.10MPa，实体模型的最大等效应力为172.56MPa，前者较后者减小了近7%。

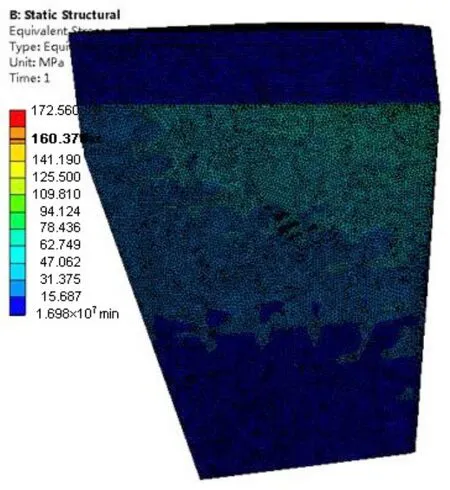
图14 实体模型的等效应力云图

图15 板壳模型的等效应力云图

4.2 结构形变

实体模型形变云图和板壳模型形变云图分别见图16和图17。在水流的冲击作用下使减摇鳍发生变形，鳍翼的形变在自由端最大，在约束端最小。板壳模型的鳍翼最大形变为 5.57mm，实体模型的最大形变为5.72mm，两者相差2.69%，相差比较小。

图16 实体模型形变云图

图17 板壳模型形变云图

5 结果分析

通过对2种减摇鳍模型进行对比可知：实体模型的厚度在制作过程中直接绘制出；板壳模型的厚度以参数的形式设置，在计算中计入其大小。2种模型本身并没有大的区别，但在网格划分上：实体模型直接画出体网格，网格数量较多且质量较差，特别是在薄壁处多以不规则的四面体为主；板壳模型先在模型表面划分面网格，再将面网格加厚，生成体网格。面网格在划分上相对简单，质量更好，数量较少，且大多生成规则的柱体网格。由于网格数量和质量的影响，在计算时间方面（以个人笔记本为例），基于板壳模型的减摇鳍计算所用时间明显比实体模型少（见表3）。

表3 减摇鳍板壳模型与实体模型计算耗时对比

经过ANSYS静力分析模块的计算获得减摇鳍实体模型和板壳模型静力响应特性，其应力和变形结果见表4，其中试验数据来自于中船重工第704研究所对减摇鳍的研究测试结果。对各项结果进行比较可知，板壳模型无论是在变形方面还是应力方面，都与试验值更接近，误差更小。

表4 减摇鳍板壳模型与实体模型计算数据对比

6 结 语

通过对减摇鳍不同结构模型进行流固耦合分析，得到以下结论：

1) 板壳模型在建模速度上与实体模型相当，但其网格数量远远少于实体模型，只有实体模型的 1/15左右，计算速度比实体模型快1倍多；对于类似减摇鳍的结构，基于板壳模型所做的分析，其计算误差相比实体模型较小。

2) 减摇鳍实体模型多采用四面体网格，板壳模型的外壳板与展向、弦向骨架部分节点没有连在一起；在水动力导入结构模型中，可能由于建模误差，力未能 100%施加上；在有限元分析中，在展向、弦向板孔处出现集中应力，虽然在细化网格后集中应力的大小和范围明显减小，但集中应力仍存在。

在实际应用中，减摇鳍与水的影响是相互的，且是多向的，单独一次流固分析不能完全反映鳍翼在实际使用中的情况，因此在后续研究中可考虑采用多向流固分析，比较不同模型的数值模拟情况。