基于改进加权质心和遗传算法的气体源定位研究
郑艳华 何永玲

摘 要: 为了提高室内危险气体泄漏点的定位精度,通过对现有气体扩散模型的研究,给出一种无风无边界连续泄漏点源浓度的扩散模型。首先应用改进加权质心定位算法通过第一次粗定位和第二次的精细定位获得定位结果。另外,利用遗传算法对室内气体泄漏源进行全局最优的精细定位,通过Matlab仿真实验进行定位误差分析,得到采用改进加权质心定位算法和遗传算法的定位相对误差分别低于5%和3.5%。最后搭建了测试系统用乙醇气体源进行泄漏点定位实验,验证了两种定位算法的准确性。
关键词: 气体源定位; 气体泄漏; 加权质心定位; 遗传算法; 误差分析; 定位验证
中图分类号: TN104?34; TP301.6 文献标识码: A 文章编号: 1004?373X(2019)20?0084?06
Research on gas source localization based on improved weighted
centroid and genetic algorithm
ZHENG Yanhua1, HE Yongling2
(1. School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China;
2. College of Medical Information Engineering, Guangdong Pharmaceutical University, Guangzhou 510006, China)
Abstract: In order to improve the positioning accuracy of indoor dangerous gas leakage points, a gas source concentration diffusion model of continuous leakage point without wind and boundary is proposed. Firstly, the improved weighted centroid localization algorithm is applied to obtain the positioning results through the first coarse localization and the second fine localization, and the indoor gas leakage source is accurately located with global optimization by means of genetic algorithm. The positioning error analysis is conducted by means of Matlab simulation experiment, the analysis results show that the relative positioning errors of improved weighted centroid positioning algorithm and genetic algorithm are lower than 5% and 3.5%, respectively. Finally, a test system is constructed to locate the leakage points with the ethanol gas source, and the accuracy of the two localization algorithms is verified.
Keywords: gas source localization; gas leakage; weighted centroid localization; genetic algorithm; error analysis; location verification
0 引 言
現代生产生活中一些大型事故,如有害化学物质泄漏、重大火灾等往往起源于易燃气体物质的泄漏,因此气体源的精准定位能够对危险区域做出预警,及时确定泄漏源位置,进而指导预防和抢救工作。气体源定位的研究成果经过移植可用于环境监测、火灾早期监测、毒气及易燃易爆气体的搜索、遇难人员搜救等场合,具有及其重要的研究意义[1?3]。当密闭化学仓储发生气体泄漏时,出于对人员安全、实时监测、数据通信等各方面的考虑,利用无线传感器网络监测是最合适的选择[4?6]。
近年来国内外众多学者在气体源无线传感器网络定位方面进行了大量的研究。现有的气体源跟踪定位方法主要有以下三种类型[7?8]:第一类是利用固定安装的监控设备定位;第二类是利用机器人(无人机等)进行移动探索定位;第三类是采用无线传感器网络方式定位。无线传感器网络由于具有组网成本低、节点放置方便灵活、覆盖范围广、能耗低、工作时间长及适用于无人看守等优点,在军事和民用领域都得到了广泛应用[9?10]。根据其具体的定位机制,可以将现有的无线传感器网络的节点定位算法分为基于测距定位算法和无需测距定位算法。基于测距定位算法通过传感器节点之间的距离、角度等信息,利用最小二乘法、最大似然估计等方法来对气体源定位[10?11];而无需测距定位算法则是利用无线传感器网络的连通性理论,如贪婪算法、质心法等推算出气体源的位置[12]。本文利用无需测距的定位方法——改进加权质心算法和遗传算法,研究在密闭化学储仓内发生气体连续泄漏时的气体源定位。
1 气体扩散模型
在气体扩散模型方面,目前大量的研究主要采用静态扩散模型。在气体源定位研究中应用最多的静态模型为高斯模型以及来源于高斯烟羽模型的气体湍流扩散模型。根据泄漏源的泄漏方式和有无风场,气体扩散模型又可以分为:无风瞬时泄漏点源的烟团扩散模型、有风瞬时泄漏点源的烟团扩散模型、无风连续泄漏点源的扩散模型和有风连续泄漏点源的扩散模型[1]。由于本文研究的是密闭化学储仓的气体泄漏问题,所以选用无风连续泄漏点源的扩散模型。无风连续泄漏点源是指由于设备破裂,导致气体持续释放出来的情况,即排除气体由于瞬间爆破释放的情况。
由菲克扩散定律可知,在气体扩散过程中,浓度随时间的变化率等于该处的扩散通量随距离变化率的负值,进而可以推导出经典的扩散方程如下:
2 无风环境下气体源定位算法与仿真
传统的气体源定位算法主要有气体源三边测量定位算法、气体源多边测量定位算法、气体源质心定位算法等。這些算法的共同特点是结合具体的气体扩散模型将气体浓度值转化为监测节点到气体源点的距离,然后代入目标函数估计源点位置。但在具体应用中,气体泄漏点源的浓度难以得知,导致传统气体源定位算法难以具体实现。本文采用加权质心定位算法先初步确定气体泄漏源的大致位置,并由此估计气体环境场源参数,再用改进的加权质心定位算法和遗传算法对气体源位置进行精确计算。
2.1 基于改进加权质心定位算法的初步定位
类比物理上的质心求解过程,在源点坐标求解过程中引入权重,由式(4)对距离d求浓度C的一阶导数得:
由此可以证明随距离的增大,浓度值下降越来越缓慢。即越靠近泄漏源,气体的浓度变化越快,所以在监测时,浓度值越大的传感器的坐标在质心算法中的贡献越大,赋予其较大的权重,按此规律,权重由下列规则给出。
设监测节点i(共n个监测点)的位置已知且分别为(xi,yi,zi),由传感器测得节点浓度ci=C(xi,yi,zi),则第i个监测节点的权重为:
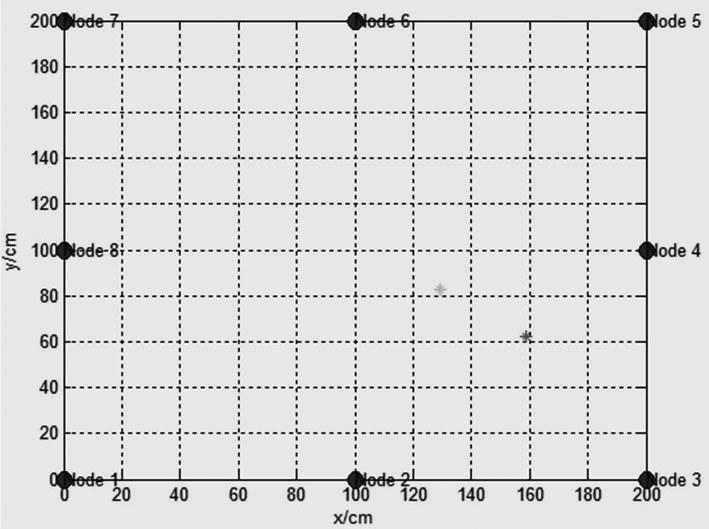
初步定位的效果如图1所示。图中靠右下角红色星点为实际气体源的位置,中间一些的绿色星点为初步定位得到的气体源点。从中可以看出两者误差较大。
2.2 测量节点数量对定位误差的影响
图1四边中所示的8个蓝点即为8个传感器测量节点布置的位置。考虑到参与算法的节点数量会影响定位效果,设计以下步骤进行测量实验。
图1 初步定位效果

1) 将8个传感器节点测量得到的浓度按从高到低排列;
2) 依次选取浓度较高的3个节点,进行100次加权质心定位算法仿真实验,求出100次仿真的平均定位误差;
3) 将选取的节点数量由3分别改为4,5,6,7,8,重复步骤1)和步骤2)。
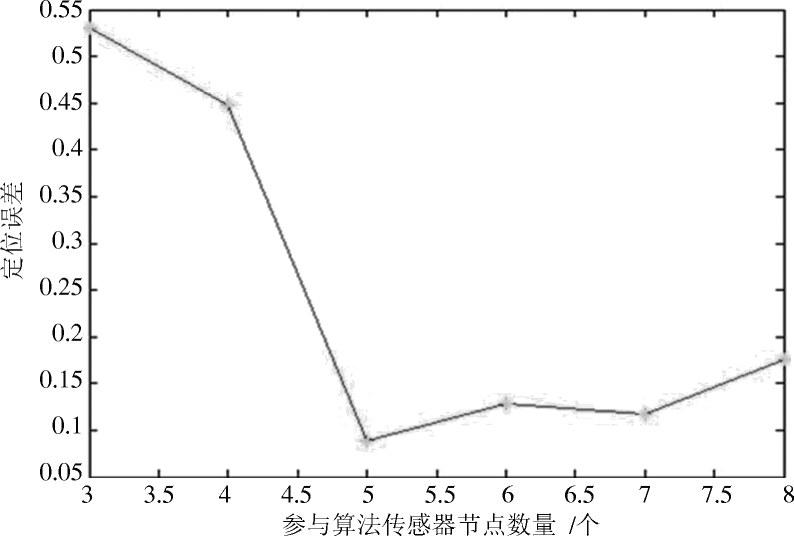
仿真实验结果如图2所示。
图2 节点数量对定位相对误差影响规律

从图中可以看出参与算法的节点数量对定位精度有较大影响。本文中的“相对误差”=真实源点与定位源点之间的距离÷检测区域的边长×100%。当参与算法的节点数量为5,6,7时,定位误差较小。结合本实验平台中的硬件设备,考虑到实际测量中传感器测量浓度时必然存在噪声,距离泄漏源越远的节点噪声对浓度值影响较大,会大大降低定位精度。因此,本文在定位算法中选取浓度较高的5个节点参与浓度监测。
进行1 000次仿真后,得到初步预测环境场源参数与真实预设环境场源参数的相对误差情况如图3所示。
由图3可以看出,在1 000次仿真中,环境场源参数P预测相对误差大部分在-0.05~0.05之间,说明这种算法预测环境场源参数P有效。预测所得P值可用于无风连续泄漏点源的扩散模型中,能为进一步精确定位提供前提条件。
图3 环境场源参数P的预测误差

2.3 基于改进加权质心的精确定位
2.3.1 算法过程
1) 以初略定位后的气体源点坐标[(x,y,z)]为中心,以比传感器包围的区域边长更小值为边长画出一个个矩形作为精细定位区域,将此区域划分成多个网格,设网格的坐标记为(x′,y′,z′)。
2) 将由初步定位中预测所得的环境场源参数P0及所测得的浓度值ci代入式(4)可以求得理想源点到各传感器节点(xi,yi,zi)的距离di。
3) 遍历格点(x′,y′,z′),计算每个格点到各传感器节点(xi,yi,zi)的距离[d′i],记误差为:
[E=i=1nd′i-di] (9)
4) 遍历格点(x′,y′,z′),寻找使得误差E取最小值的格点,记下其坐标值(xo,yo,zo)即为精细定位结果。
2.3.2 算法仿真
精细定位的详细仿真步骤如下:
1) 随机产生场强Q、扩散系数K、源点平面坐标(x,y)。
2) 记录各传感器测量节点的坐标(xi,yi),标出各传感器测量节点的位置。
3) 计算各传感器测量节点(xi,yi)到源点(x,y)的距离。由式(4)计算各节点浓度值ci,由改进的加权质心定位算法(式(6)、式(7))先初步确定气体泄漏源的大致位置[(x,y)],并由式(8)估计气体环境场源参数P0。
4) 以初略定位坐标[(x,y)]为中心,以传感器包围的矩形边长的10%为边长画出一个个矩形作为精细定位区域,将此区域划分成100个网格,各个格点坐标记为(x′,y′)。
5) 由初步定位中预测所得的环境场源参数P0代入式(4)可以求得试验源点(x,y)到各传感器测量节点(xi,yi)的距离di。
6) 遍历格点,计算每个格点(x′,y′)到各传感器节点(xi,yi)的距离[d′i],记误差为[E=i=1nd′i-di]。寻找使得E取最小值的格点,记下其坐标值[(xo,yo)],即为精细定位结果。
用Matlab编程画出误差E关于坐标的函数平面图如图4所示(四边的8个实心蓝点为浓度测量传感器节点坐标,红色的十字星点为随机产生源点坐标,绿色的星形点为初步定位坐标,蓝色圆圈为精细定位坐标),找到使得E取最小值的格点(图中蓝圈),记下其坐标值(xo,yo)即为精细定位结果。
图4 改进加权质心算法的一次定位结果
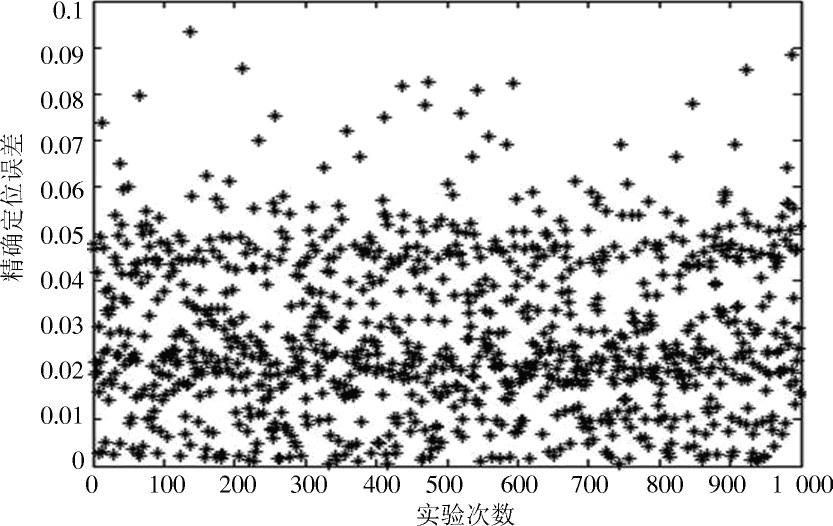
利用改进质心初步和精确定位算法,通过Matlab进行1 000次仿真,得到相对误差如图5所示,可见绝大多相对数误差在5%以下。
图5 1 000次仿真实验相对误差分布
2.4 基于遗传算法的气体源定位
8个传感器测量节点如图1所示布置,从左下角开始按逆时针方向分别将节点标记为1~8。先对测量区域进行象限粗划分,并将其分为如笛卡尔平面坐标系的4个象限,再应用遗传算法对气体源定位。基于遗传算法的气体源定位算法的具体步骤如下。
1) 用改进加权质心定位初步定位算法反推出环境场源参数P,结合式(4)便可求得各传感器节点到源点的距离di。
2) 在传感器检测节点1,3,5,7的浓度值中选取浓度较高节点所对应的象限,记为区域I。
3) 再将区域I的象限划分为边长为较小(如1 cm)的格点,记下各个格点的坐标(x″,y″)。
4) 遍历区域I中所有的格点(x″,y″),计算每个格点到各传感器节点的距离[d′i],记误差为[E=i=1nd′i-di]。
5) 对选定区域I中所有的格点进行编码,得到种群编码,选择适应度函数[D=1E],并通过遗传算法中的选择、交叉对个体进行筛选和进化,使适应度值大的个体被保留,小的个体被淘汰,新的群体继承了上一代的信息,又优于上一代,这样反复循环,直至满足条件(如D>0.95)。最后留下来的个体集中分布在最优解周围,筛选出其中最优的个体作为问题的解。
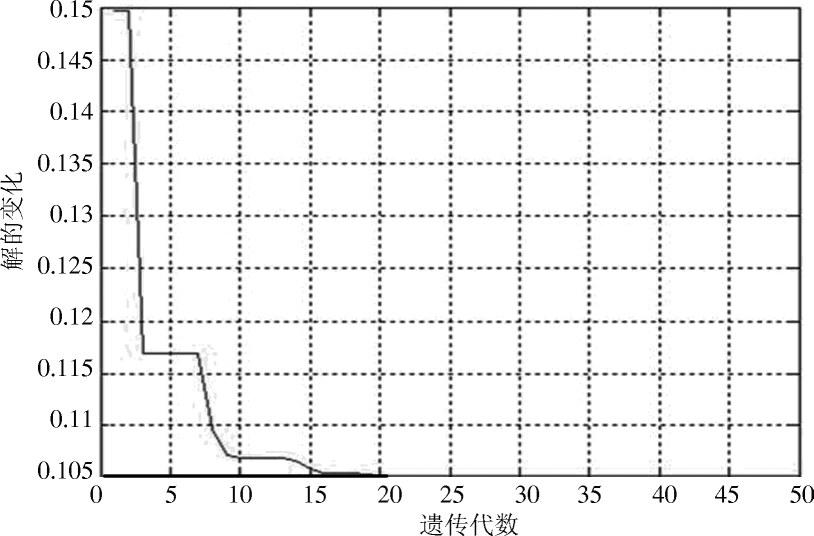
图6为基于遗传算法的进化过程。可以看出,经过20代左右的进化就可以达到较精确的坐标定位。
图6 遗传算法最优解的一次进化过程
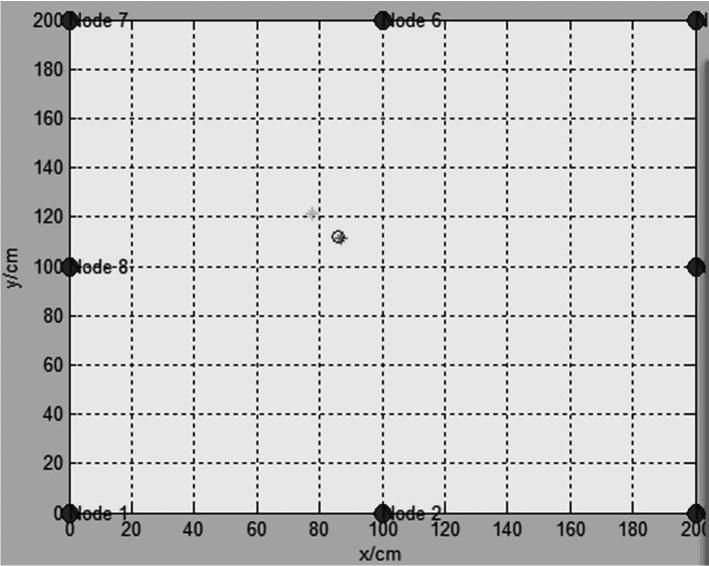
基于遗传算法的一次定位实验如图7所示。其中红色星点为实际气体源点位置,蓝色圈则为基于遗传算法得到的定位点;图中横坐标和纵坐标的单位均为cm。可以看出它们之间的误差较小。
利用遗传算法进行1 000次仿真实验的定位相对误差如图8所示。可见,相对误差绝大多数在3.5%以内,求得1 000次仿真实验的平均误差不超过2.1%。
图7 遗传算法一次定位效果

圖8 基于遗传算法的1 000次仿真定位误差

3 实验验证
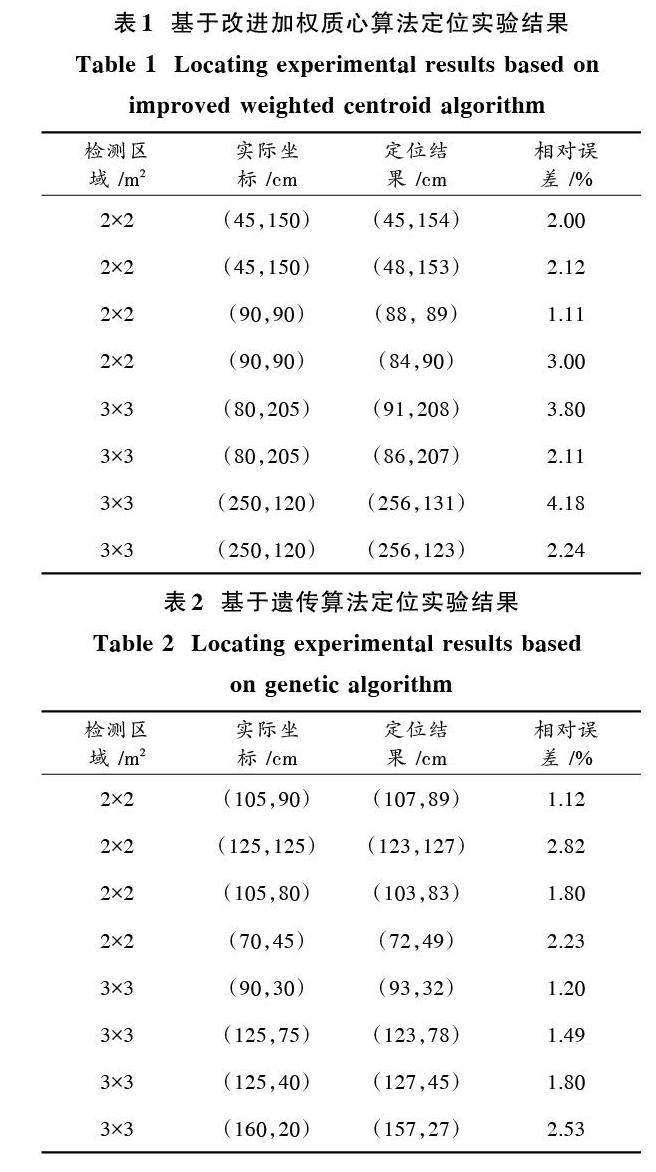
根据改进加权质心定位算法和遗传算法,本文设计气体源定位实验系统。该系统主要包含前端的采集部分、中端的发送部分和终端的定位结果显示平台三大部分。前端包括气敏传感器TGS2620 和节点处理器CC2530;中端使用ZigBee 2007协议无线传感器网络传递数据;终端主要分为无线传感器网络的协调器和显示平台两部分。协调器与显示平台通过串口通信传递数据。基于STM32F407的显示平台具有数据文件保存功能,方便实验数据的后期处理。在25 m×10 m的密闭实验室内分别进行面积为2 m×2 m和3 m×3 m的乙醇气体源定位实验,定位结果如表1和表2所示。
从表1、表2中可以看出,利用搭建的实验平台得到的真实气体定位实验结果表明,在检测区域面积为2 m×2 m,3 m×3 m的情况下定位误差较小,与仿真实验结果基本相符。本文所做实验均采用乙醇气体,该定位算法及定位系统对其他化学气体源的定位也具有借鉴意义。
4 结 论
本文结合无风连续泄漏点源的扩散模型提出基于加权质心算法的精细定位算法和基于象限粗划分的遗传定位算法。通过Matlab编程进行仿真,这两种算法均能有效地进行气体泄漏源的定位,且相对误差较小。利用搭建的实验平台也证实了两种算法对乙醇气体源在仓储中进行无风扩散时定位的准确性。
参考文献
[1] 彭宇,王丹.无线传感器网络定位技术综述[J].电子测量与仪器学报,2011,25(5):389?399.
PENG Yu, WANG Dan. A review: wireless sensor networks localization [J]. Journal of electronic measurement and instrument, 2011, 25(5): 389?399.
[2] 张园园,张巨伟,尚思思,等.泄漏气体扩散模型的研究与应用[J].当代化工,2013(4):507?509.
ZHANG Yuanyuan, ZHANG Juwei, SHANG Sisi, et al. Research and application on diffusion model of leakage gas [J]. Contemporary chemical industry, 2013(4): 507?509.
[3] CAO M L, MENG Q H, WU Y X, et al. Consensus based distributed concentration?weighted summation algorithm for gas?leakage source localization using a wireless sensor network [C]// Chinese Control Conference. Xian: [s.n.], 2013: 7398?7403.
[4] 秦晓鑫,王文军,尹长川.一种基于无线传感网络的气体泄漏源定位算法[J].软件,2013,34(1):111?115.
QIN Xiaoxin, WANG Wenjun, YIN Changchuan. A localization algorithm for gas leakage source based on wireless sensor network [J]. Software, 2013, 34(1): 111?115.
[5] LI Q M, LIU Z G, WANG J K, et al. A gas source localization algorithm based on wireless sensor network [C]// Proceeding of 11th World Congress on Intelligent Control and Automation. Shenyang: IEEE, 2015: 2514?2518.
[6] WU Y X, HAO M, ZHANG Y, et al. Single gas source localization using a mobile sensor network [C]// Abstracts of the International Conference on Advanced Mechatronics: Toward Evolutionary Fusion of IT and Mechatronics. [s.l.]: IEEE, 2010: 177?182.
[7] VUKA M, SCHAFFERNICHT E, SCHMUKER M, et al. Exploration and localization of a gas source with MOX gas sensors on a mobile robot?a gaussian regression bout amplitude approach [C]// 2017 ISOCS/IEEE International Symposium on Olfaction and Electronic Nose. Montreal: IEEE, 2017: 1?3.
[8] WIEDEMANN T, SHUTIN D, HERNANDEZ V, et al. Bayesian gas source localization and exploration with a multi?robot system using partial differential equation based modeling [C]// ISOCS/IEEE International Symposium on Olfaction and Electronic Nose. Montreal: IEEE, 2017: 1?3.
[9] 陈立伟,杨建华,孙亮,等.基于分布式传感器阵列的静态气体源定位方法[J].电子科技大学学报,2014,43(2):212?215.
CHEN Liwei, YANG Jianhua, SUN Liang, et al. Odor source localization algorithm based on spatially distributed sensors array [J]. Journal of University of Electronic Science and Technology of China, 2014, 43(2): 212?215.
[10] LI Q M, LIU Z G, WANG J K. Non steady gas source localization algorithm for indoor environment using WSN [C]// 2016 Chinese Control and Decision Conference. Yinchuan: IEEE, 2016: 1782?1786.
[11] ZHANG Y, ZHANG L, HAN J, et al. An indoor gas leakage source localization algorithm using distributed maximum likelihood estimation in sensor networks [J]. Journal of ambient intelligence & humanized computing, 2017(2): 1?10.
[12] BI Y W, GU Y T. Study on gas leak source detection and localization based on greedy approach [J]. Computer simulation. 2014, 31(1): 286?289.

