基于多指标的文献关联程度研究：合理性考察

郭 强，赵 瑾（.郑州大学信息管理学院；.中国人民解放军陆军军官学院军事运筹教研室）

文献的共引次数与文献之间的关联程度具有较好的正相关性，因而可以利用共引次数对文献的关联程度进行表示，并在此基础上对结构关系进行探讨，从共引次数可以拓展至其他的文献关联指标，［1-4］由此会涉及到关联程度的多指标情形，如对研究前沿的探测。已有的研究包括利用不同的关联指标得到不同的探测方法，以及对不同探测方法的有效性的比较。［3-8］目的是使对结构关系以及研究前沿的揭示能够更具有有效性和针对性。多指标的纳入会使对关联程度的描述更全面，可以考虑将分别建立在不同关联指标上的文献结构以及探测结果进行综合考量，也可以考虑先对不同的关联指标进行综合，其中综合的方式有所不同。［3,9］本研究先对关联指标进行综合，综合的方式是给出关联程度的多属性描述以及相应的综合关联程度，并在综合关联程度的基础上对结构关系进行探讨。

此外，多指标的纳入和对综合关联程度的考察，会有助于对某一领域的专业方向的揭示，包括聚类关系的合理性以及对专业方向的定性。

对综合关联程度的考察包括指标的选取、指标合成方式的探讨、综合关联程度的获取流程以及对综合关联程度的合理性的衡量。

1 关联指标的直接合成

在对关联指标直接合成的情形下，对于选取的非样本文献而言，指标之间相关系数的绝对值的最大值仅为0.520，绝对值小于0.5 的情形具有相对较高的比例。尽管能够通过巴特莱检验，但是KMO 值仅为0.513，说明对指标直接合成时没有将原始指标转化为相应的独立变量。由于原始指标均具有正向性，对于此时的非样本文献，当某个原始指标增加且其余指标保持不变时，文献的关联程度会有增加的趋势。又由于此时的原始指标之间具有较弱的样本相关性，拟合方程可以近似为原始指标的直接求和，其中的拟合值可以作为非样本文献关联程度的近似值。

当非样本文献调整时，确定关联程度的过程也会有改变。对于选取的非样本文献而言，如果指标之间具有较强的相关性，那么在指标合成时需要将原始指标转化为相应的独立变量，此时可以考察指标的主成分。首先，当确定主成分的大致含义并且从总体上判断各个主成分的含义均具有正向性时，得到的主成分及其含义反映的是非样本文献的性质。而在对主成分与关联程度的关系进行考察时，通常需要借助得到的主成分的含义，并从总体上进行判断，这样在该过程中主成分的含义应该是样本意义上的概念。而对主成分的含义从总体上进行判断，由此得到的正向性则为总体上的概念。对于样本或非样本文献而言，当某个主成分增加且其余主成分保持不变时，文献的关联程度会有增加的趋势，又由于得到的主成分之间具有独立性，此时的拟合方程可以近似为对主成分的直接求和，拟合值可以作为对非样本文献关联程度的近似。其次，当确定了主成分的大致含义，但是主成分的含义从总体上与关联程度之间的正向性或负向性并不显著时，需要考虑两者的非线性关系。如果能够明确两者的非线性关系，那么可以确定或近似相应的拟合方程，非样本文献的关联程度可以用拟合值近似；如果不能完全确定两者的非线性关系，由于非样本文献的实际关联程度是未知的，需要判断主成分的大致含义及其在总体上与关联程度之间的关系，由此来近似非样本文献的主成分取值与非样本文献的关联程度的关系。当对非样本文献建立拟合方程时，主成分含义在总体上与关联程度之间非线性关系的不明确会对方程的确定或近似带来影响。在该情形下可以考察非样本文献的概率型综合关联程度。第三，当主成分的大致含义尚无法确定时，可以通过正交旋转使新生成的因子更具有可解释性。在此基础上如果能够确定生成因子的大致含义，则根据因子含义从总体上判断具有正向性并转入上述第一步中，否则转入第二步；如果生成因子的大致含义仍然无法确定，可以转入非样本文献的概率型综合关联程度。

对于所选取的非样本文献而言，在旋转后的成分矩阵中，不同的原始变量只与不同的因子具有较好的相关性，且每个原始变量在相应因子上的载荷均大于0.9，同时在其余因子上的载荷的最大值仅为0.278。由于采用的是正交旋转，载荷可以反映原始变量与因子的相关性，此时原始变量相互之间呈现弱相关，这和上述对非样本文献的考察结果是一致的。另外，在对指标直接合成的情形下，同样的两篇文献，如果属于两组不同的非样本文献，由于在上述过程中关联程度的近似值是取决于所属非样本文献的性质的，那么得到的关联程度的近似值可能也会有所不同。

2 概率型综合关联程度

在概率型综合关联程度的情形下，需要考察自变量的共线性。对于文献《基于多指标的文献关联程度研究：指标的合成》图4 中的样本文献，XTX 的特征值分别为1.706、1.502、1.027、0.942、0.589、0.233，最大特征值与最小特征值的比值为7.322，从条件数的角度来看模型的共线性偏弱或可以近似为没有共线性。此外，每个自变量与其余自变量的复相关系数以及相应的方差扩大因子分别为1.957、1.916、1.357、1.107、1.164、1.770，其中最大值也没有超过经验标准，从方差扩大因子的角度来看，模型不存在中等或较强的共线性，各个自变量近似为不包含在某些共线关系中，这样可以对原有的自变量直接建立模型。利用Spss 对文献《基于多指标的文献关联程度研究：指标的合成》 图4 中的文献关联指标与文献之间的关联等级进行逻辑回归，参数向量的检验结果显示：在0.05 水平下所选取的关联指标在整体上的影响是显著的，并且各个自变量相应的p 值均小于0.05。由样本文献得到参数的估计以及相应的经验回归方程，其中截距的估计值分别为7.8206、11.2747、16.6736、23.0218，其余参数的估计值分别为-0.9539、-0.6533、-1.2947、-1.5590、-11.8506、-5.4366，这些参数的估计值均为负数，这是由于选取的指标均具有正向性，当某个自变量增加且其余的自变量保持不变时，两篇文献的关联程度处于某个关联等级的概率与处于高于该关联等级上的概率的比值会有减小的趋势。

在经验回归方程的基础上给出文献之间的关联程度处于各个关联等级上的预报概率，由此可以考察样本关联程度的预报结果与样本实际关联程度的一致性。对于文献《基于多指标的文献关联程度研究：指标的合成》图4 中的样本文献，预报与观测的一致比能够达到94.2%，这是由于以下几点。①图4 中的样本文献是在满足样本文献选取要求，并对初步选取后的文献进行调整得到的，在调整时仍需要满足样本文献的选取要求，其目的是使自变量的影响均是显著的，并由此可以按照传统的过程得到相应的预报概率及其置信区间。［10］否则将影响所形成的模型和估计，毕竟在这里认为关联程度和所选取的自变量在总体上均具有关联性，而这种有偏差的估计与预报以及预报的效果还需要做进一步的探讨。② 当样本容量较小时，选取满足要求的样本后，需要进行相应的显著性检验，在此基础上决定是否需要对得到的文献进行调整。但是随着样本容量的增加，样本的性质会趋于总体的性质，样本可以对各个关联指标与关联程度之间的相关性进行反映，从而使解释变量的影响具有显著性，这样就不需要对文献进行调整了。

对于选取的非样本文献而言，由经验回归方程得到文献关联程度处于各个关联等级上的预报概率和相应的关联程度的期望分值，其中对各个关联等级赋予的关联分值为1-5 分。在关联程度的期望分值的基础上，得到由任意两篇文献分别与其余文献的期望分值所形成的向量，利用向量的夹角余弦衡量两个向量的相似度，两个向量的相似度越高意味着两篇文献与其余文献的期望分值会具有更好的相似性，从而这两篇文献也会具有更好的相似性。这里将向量的夹角余弦作为两篇文献的相似性度量，又因为关联程度的期望分值均为正数，夹角余弦的取值介于0-1，文献之间的距离等于1 减去夹角的余弦。在文献距离的基础上可以对非样本文献的结构关系进行显示并对其合理性进行考察，如通过Excel 由关联程度的期望分值分别得到每两篇文献与其余文献所形成的向量的夹角余弦，用1 减去向量的夹角余弦后，将得到的距离矩阵作为输入，通过Spss 得到非样本文献的二维分布情况。

3 合理性考察

图1 为对指标直接合成时的情形。对选取的非样本文献而言，其关联程度可以近似为对原始指标的直接求和，文献的相似性度量以及对文献距离的表示与在概率型综合关联程度中所采取的方式相同，目的是使得到的结构关系具有可比性。另外，指标的取值为标准化后的取值。同时需要指出以下几点。① 由于选取非样本文献时没有对文献关联指标的取值范围作要求，当某篇文献与另一篇文献的关联程度不为零，且与其余文献的关联程度均为零时，这两篇文献的夹角余弦的分母等于零，由此需要剔除非样本文献中的部分文献，从而使不同文献关联程度情形下的考察文献不仅相同而且其中任意两篇文献的夹角余弦也均具有意义，由此夹角余弦的分母为零的情形不影响所得结构关系的可比性。而当文献关联程度为零的情形增多时，需要剔除的文献数量也会有增加的趋势。②当某两篇文献同与除这两篇之外的少量单篇或是多篇文献的关联程度不为零，且与其余文献的关联程度均为零时，与这两篇文献相对应的向量有可能会具有很好的相似度，特别是当两篇文献只与除这两篇文献之外的某单篇文献的关联程度不为零时，这两篇文献的夹角余弦等于1。因此，当关联程度为零的情形较多时，会出现文献之间的距离很小以及为零的情况，这样在非样本文献的二维分布中会表现为文献位置的重合或近似重合。

图1 指标直接合成时的情形

图2 概率型综合关联程度的情形

图3 只考虑共引次数的情形

图2 为概率型综合关联程度的情形。关联程度的期望分值是各个等级的关联分值与文献关联程度处于相应等级上的预报概率的乘积的累计和。由于处于各个等级上的概率之和等于1，期望分值的最小值为各个等级的关联分值的最小值，对于所考察的非样本文献而言，不同文献之间的关联程度均大于等于1，且均不会等于零，这也是与图1 相比文献位置重合的情形相对较少的原因。

图4 专家对关联程度进行判断时的情形

图3 只考虑共引次数的情形。图4 为专家对非样本文献的关联程度直接判断的情形。其中，关联程度是根据文献的内容在0-10 分进行打分。图1 至图4文献位置之间的距离的相对大小具有大体上的一致性。但是这种比较是建立在对非样本文献相互之间的相似性或是距离进行近似的基础上，由此可以考虑从相似性或是距离衡量不同情形的合理性。如将专家判断文献关联程度的情形作为标准，考察不同情形中文献之间的距离关系与标准情形中文献之间的距离关系的一致性。在每种关联情形中均能得到每篇文献与其余文献之间的相似度，在某种关联情形中，用某篇文献与其余文献之间的相似度和在标准情形中的同一篇文献与其余文献之间的相似度的等级相关系数来衡量两种情形中某篇文献与其余文献的相似度的相对大小的一致性。这样每篇文献均有相应的等级相关系数与其相对应。在此基础上用所有文献的等级相关系数的平均值来衡量两种情形中单篇文献与其余文献相似度的相对大小的一致性。

对于概率型综合关联程度与专家判断关联程度这两种情形而言，得到相关系数的平均值为0.580。但是在对指标直接合成的情形中，如果文献之间关联程度为零的情形相对较多，那么文献夹角余弦中分子为零的情形也会相对较多。在专家判断关联程度的情形中，某篇文献与其余某两篇文献之间具有不同的相似度，在对指标直接合成的情形中可能会由于这篇文献与其余两篇文献之间的相似度均为零而使得文献之间会具有相同的相似度，由此与每篇文献对应的等级相关系数会相对较低，甚至相关系数可能会为负数。而当某篇文献的相关系数为负数时，可将两种关联情形中的该篇文献与其余文献的相似度的相对大小的一致性取为零，并在此基础上得到一致性的平均值，如对指标直接合成与专家判断关联程度这两种情形的相关系数的平均值为0.018。另外，在某种情形中可以设定某个阈值，对于大于等于该阈值的文献相似度，考察这些相似度的相对大小能够在多大程度上与专家判断关联程度的情形相吻合，并用此来判断给定阈值时的某种关联情形与专家判断关联程度情形的一致性。如，选取阈值为0.03，在某种情形中，对于某篇文献而言，只考虑与该文献的相似度大于等于0.03 的其他文献，并考察某种情形中该文献与这些文献的相似度和在专家判断关联程度情形中的这篇文献与这些文献的相似度的等级相关系数。每篇文献均有相应的等级相关系数与其对应。在某种情形中，如果某篇文献与其他文献的相似度均小于0.03，以及某篇文献只与其余某一篇文献之间的相似度大于等于0.03，那么这两种情况中的文献是不计入在内的。当给定阈值时，每篇文献的等级相关系数体现某种关联情形对专家判断关联程度情形中的该篇文献与相应文献之间的相似度的相对大小的保持程度，这里仍然是利用每篇文献的等级相关系数的平均值近似衡量给定阈值时的某种关联情形与专家判断关联程度情形的单篇文献与其余文献相似度的相对大小的一致性。

另外，考察文献之间相似度的相对大小时，可以对每篇文献进行考察，也可以对所有文献相互之间的相似度的相对大小直接进行考察。当不设定阈值时，能够得到某种关联情形的所有文献之间的相似度和标准情形中的相应文献之间的相似度的等级相关系数，如果一致性较高，那么建立在文献距离相对大小基础上的聚类结果也可能会具有较好的一致性；当设定阈值时，只考虑某种情形中的大于等于阈值的文献相似度，并考察这些相似度的相对大小在多大程度上与标准情形相吻合。

图5、图6 为上述前三种情形分别与专家判断关联程度情形的相关情况，其中横轴为阈值。图5 是对每篇文献分别考察的方式，图6 是对所有文献直接考察的方式。图6 将所有的文献均考虑在内，是对应阈值为零的情形。对于情形一而言，在对每篇文献分别考察的方式中，当阈值由0.03 增加至0.1 时，相关情况会保持不变，这说明情形一中的相似度是分布在小于0.03 以及大于等于0.1 的范围。在对所有的文献直接考察的方式中，阈值取为0.03 是对应于相似度大于等于0.03 时文献相似度的相对大小与实际情况的一致性。

此外，对于所选取的非样本文献，在对每篇文献分别进行考察的方式中，情形一的相关情况会好于情形二和情形三。同时由于无论是单指标情形还是多指标情形，关联指标对文献关联程度的反映均是基于两者之间统计意义上的正相关性，因而会出现单指标描述好于多指标描述的情况，如图5 中情形三的一致情况要好于情形二。在对所有文献考察的方式中，当阈值大于零且小于等于0.5 时，与其余的区域相比，这三种情形的相关情况会相对较为接近，但是情形三的一致情况要好于情形一和情形二；而当阈值大于0.5 时，情形一和情形二的一致情况均会好于情形三。从整体上看，对于这里选取的非样本文献而言，多指标描述并不明显地好于单指标描述，但是当各个阈值处对应的文献数量均足够多时，多指标描述在整体上好于单指标描述，这是建立在多指标描述对于关联程度的反映会好于单指标描述的直观认识基础上，由此多指标描述中的关联分值的相对大小与实际情况会具有更好的一致性。另外从整体上看，随着阈值的变化，多指标描述与单指标描述会具有相似的变化趋势。

图5 对每篇文献分别进行考察的方式

4 说明

4.1 存在共线性的情形

在概率型综合关联程度的情形下，由于从直观上选取的文献关联指标并不独立，选取样本文献的某些关联指标有可能会具有很好的样本相关性，使某些自变量包含在某些共线关系中。在这里构造以下样本，使共引次数与相同的参考文献数量具有很好的相关性，并且其余的指标取值与文献《基于多指标的文献关联程度研究：指标的合成》图4 中的原有指标取值相同。当调整相同的参考文献数量时，如果参考文献的杰卡德指数保持不变，那么两篇文献总的参考文献数量需要作相应的改变，当杰卡德指数给定时，对其分子与分母的取值没有限制，只不过不同的取值情形其发生的概率会有所不同。

图6 对所有文献直接进行考察的方式

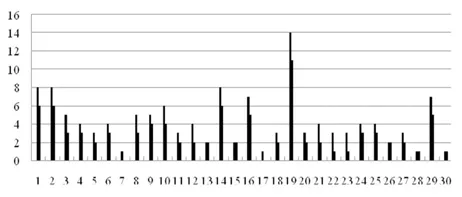
图7 构造的样本文献

如果取到了这样的样本（见图7），其中仅列出了文献的共引次数与相同的参考文献数量，除了相同的参考文献数量之外，其余变量的取值与文献《基于多指标的文献关联程度研究：指标的合成》 图4 中的相应变量的取值相同，在这里使得文献的共引次数与相同的参考文献数量的相关系数为0.974。对于该样本可以得到XTX 的特征值分别为2.162、1.500、1.002、0.800、0.518、0.018，其中最大特征值与最小特征值的比值达120.111，这样标准模型会存在中等程度的共线性。同时得到的方差扩大因子分别为28.571、27.027、1.377、1.109、1.085、1.852。从方差扩大因子的角度来看，模型也存在共线性，并且前两个变量——共引次数与相同的参考文献数量均包含在某些共线关系中。

通过主成分回归消除共线性，得到XTX 的特征向量以及相应的主成分，其中主成分为Z6=0.713X1-0.692X2-0.051X3-0.014X4-0.016X5+0.097X6，由于XTX 的第六特征值仅为0.018 且等于Z6的方差，可以认为Z6中的变量组合具有较高的共线性，同时在该变量组合中X3、X4、X5、X6的系数和X1、X2的系数相比均相对较小，且X1、X2的系数的绝对值可以进行比拟，X1、X2具有很好的取值一致性，而这和X1、X2较高的相关系数是一致的。由于前四个主成分的特征值的累计和占特征值总和的91.1%，因而选取前四个主成分进行回归，这样剔除Z6，同时信息损失也在可以接受的范围内。在相应的经验回归方程中，将主成分还原为原始变量后，可以得到以原始变量作为自变量的经验回归方程，这样方程中的所有原始变量都得到了保留。

4.2 统计意义上的客观性

利用共引次数衡量文献之间的关联程度具有客观性，但是这种客观性是统计意义上的客观性，对于共引次数这个单指标而言，从直观上会存在不客观的情形。如，当文献的共引次数给定且较高时，文献之间的关联程度并不确定，会存在一定的变化范围，文献之间的关联程度有可能是偏高的，但是此时的共引次数或此时的关联分值却是较高的，由此会出现关联分值与文献实际关联程度不一致的情形。在共引次数的基础上对文献结构考察时，这两篇文献有可能会被归于某一子类，而实际上这两篇文献是不应归于一类的，由此带来了不客观的结构划分。又如在一定的取值范围内，共引次数较小的两篇文献之间的关联程度未必会比共引次数较大的两篇文献的关联程度低。由此利用共引次数来表征文献之间的关联程度时会有不客观的情形出现，相应地也会带来后续结构划分上的不客观。假设考虑三篇文献，文献A 与文献B 以及文献A 与文献C 的关联分值均低于文献B 与文献C 的关联分值，这样在某细化程度下，文献B 与文献C 会被归于一类，而文献A 会单独成类。但实际上将文献A 与文献B 归于一类，且文献C 单独成类却是符合实际情况的。尽管利用共引次数衡量关联程度会具有一定的非客观性，但是当样本容量较大时，上述关联分值不客观情形的占比应当会相对较小，毕竟此时的关联分值也就是共引次数，与文献之间的实际关联程度会具有较好的正相关性，因而共引次数与文献关联程度大小关系相一致的情形会具有较大的比例，这也是这里的关联分值具有客观性，从而建立在该关联分值基础上的结构划分也会在总体上具有客观性。

利用多指标衡量文献之间的关联程度时会有类似的情形，得到的关联分值在总体上可能会具有客观性。如对多指标直接合成时，如果可以从主成分与各个指标的相关性大致判断主成分的含义，并且根据主成分的含义可以判断各个主成分均具有正向性，那么当两篇文献的各个主成分具有较高的取值时，得到的关联分值也会较高。当各个主成分均具有正向性时，各个主成分的取值较高，意味着文献之间的关联程度的期望值也会较高，由此这两篇文献之间的关联程度有可能只是偏高的，这样就可能会有关联分值与实际关联程度不一致的情形出现，而这种关联分值与关联程度的不一致有可能会带来后续不客观的结构划分。

从样本出发得到的关联分值也会有类似情况。在样本中，如果某两篇文献的关联指标的取值较高，并且相应的关联分值也较高，那么当两篇非样本文献的关联指标的取值与这两篇样本文献的关联指标的取值相近时，由于回归方程的连续性，非样本文献的关联程度处于各个关联等级上的概率可能会与样本文献情形下的概率相接近，因为关联分值是关联程度处于各个关联等级上的概率与各个关联等级分值分别相乘后再进行求和，所以非样本文献的关联分值也可能会较高。但实际上，当关联指标的取值较高时，非样本文献的关联程度有可能只是偏高的，这样在关联分值基础上的结构划分可能会出现与实际情况不相符合的情形。

与共引次数的情形相类似，多指标情形中关联分值的不客观占比有可能不高，究其原因是由于关联分值与实际关联程度可能会具有正相关性，而这实际上也是关联分值及其获取方法是否具有合理性以及有效性的一种基础。对于指标直接合成这种情形而言，如果各个主成分均具有正向性，那么任意主成分增加且其他主成分保持不变时，关联程度的期望值会增加，如此可以对各个主成分直接进行求和来对关联程度的期望值进行近似，而各个主成分的和值也是这里的关联分值，关联分值实际上也是对关联程度的期望值的近似。由于从直观上关联指标与关联程度之间会具有较好的相关性，当关联指标增加时，关联程度会有增加的趋势，关联程度的期望值也会有增加的趋势，关联分值也可能会有增加的趋势。由此关联指标与关联分值之间可能会具有正相关性。考虑到关联指标与关联程度会具有较好的正相关性，则关联分值与关联程度之间也可能会具有正相关性。

同样地，对于从样本出发得到的关联分值而言，由于从直观上关联指标与关联等级在总体上会具有较好的正相关性，当样本容量足够大时，如果关联指标的取值增加，那么相应的关联等级也会有提高的趋势。因为在得到回归方程时是使得由回归方程得到的关联程度处于各个关联等级上的概率能够尽可能地与样本相接近，所以回归方程是对样本的近似，不严格地说，回归方程可能也会具有和关联指标与关联等级之间的正相关性相类似的性质。对于回归方程而言，由于给出的是关联程度处于各个关联等级上的概率，回归方程可能会表现为具有当关联指标较高时关联程度处于较高关联等级的概率会较高的趋势，或回归方程可能会具有这样的性质。如果回归方程通过显著性检验，那么可以利用回归方程对非样本文献之间的关联程度进行预报，能够给出关联程度处于各个关联等级上的概率。由于当非样本文献的关联指标较高时，得到的关联程度处于较高等级上的概率可能也会有较高的趋势，相应的关联分值可能也会有较高的趋势，这样对于非样本文献而言，关联指标与关联分值之间可能就会具有正相关性，而从直观上关联指标与实际关联程度会具有较好的正相关性，关联分值与实际关联程度也可能会具有正相关性。需要指出的是，上述的讨论并不严格，如关联指标较高是指各个指标的取值在整体上较高。这与共引次数相类似，在总体上利用多指标得到的关联分值可能会具有客观性，不客观情形的比例可能会较小，同时不客观情形的占比应当和关联指标与关联程度之间的统计相关性以及对多指标的合成方式有关。