酿酒制造业上市公司技术革新与企业绩效的相关性实证研究

黄 妍，刘 青，黄亚东

（江苏食品药品职业技术学院，江苏淮安 223002)

随着经济全球化的飞速发展，不仅人们的生活水平在不断提高，我国的科技也是在不断蓬勃发展，但是从整体上看，我国依然存在创新能力不强，科技发展水平不高的状况。而技术革新能力关乎企业的生存和发展，党的十九大报告中也指出要加快建设创新型国家，加强国家创新体系建设，强化战略科技力量，表明了无论是国家还是企业都认识到了创新的重要性和意义。因此，在这样的市场经济环境中，企业必须不断提高企业核心技术水平，维持企业核心竞争优势，才能获得持续生存和发展的机会。

酒精及饮料酒制造业在我国有着悠久的历史，经历了辉煌的发展时期和发展历程，为我国的经济发展做出了不朽的贡献，但是随着新工业的产生和不断崛起，酒精及饮料酒制造业因为创新力的不足和技术革新发展速度较慢等原因，带来了发展上的阻碍。并且因为近年来国家宏观制度的调控，政策的不断改变，与之相关的部门和政府单位对酒精制造业的要求也不断趋于严格，这些政策的实施对酒精制造业的健康发展也产生了不同程度的影响。因此，要想改变消极的市场现状，就要求酒精及饮料酒制造业提升自身的创新能力，发展属于自身的核心竞争力，保持和巩固其在行业中的地位。

1 文献综述

研发支出对企业绩效有着密不可分的影响，因此研究研发支出对企业绩效的影响也就成为了学者的研究热点。学者对于研究企业研发支出与企业绩效之间的关系，基本采用实证分析方法，论证二者是否具有相关关系，有着怎样的相关关系。根据现有的研究文献，学者对研发支出与企业绩效之间的相关性结论大致分为以下3种。

1.1 研发支出对企业绩效呈现显著正相关关系

梁莱歆、张焕凤[1]研究发现，高科技企业研发支出强度与企业盈利能力和成长能力之间存在着显著的正相关关系，而研发投入对后续年度企业绩效的产出效应呈逐渐下降趋势。程宏伟、张永海等[2]运用96 家高新技术企业上市样本数据进行实证研究和分析，研究结果表明，研发投入对企业绩效有正向影响，但是随着年份的延长，这种影响将逐渐减弱，同时也发现高新技术企业整体研发投入水平较低。彭泽瑶、黄德忠[3]在对汽车制造业的实证研究中，得出该行业的研发支出与企业绩效呈显著正相关关系，并且这种关系的影响未表现滞后性。同样的，外国学者Garner、Nam 等[4]研究了243 家互联网和生物制药企业，并且在研究研发投入与企业绩效关系的同时，引入创新速度，结果同样表明，研发投入与企业绩效存在正相关关系。Ren 和Eisingerich在对中小企业绩效进行实证研究中也发现，研发投入的增长会对企业绩效产生积极的影响。

1.2 研发支出对企业绩效呈现负相关或不相关关系

游春[5]以沪市A股中小企业上市公司信息为研究数据，研究表明，R&D 支出与ROE 所代表的企业绩效不相关。陆玉梅、王春梅[6]以2005年—2008年连续3年99 家制造业和信息技术业上市公司研发投入数据为研究基础，实证研究结果表明，研发投入强度与当期的企业绩效的关系表现为负相关。李中、周勤[7]也在上市公司的实证研究中证实了，研发投入与企业绩效呈负相关关系。此外，杨剑发现，研发密度对企业绩效的影响是呈非线性关系的，这意味着研发支出对企业绩效的影响呈先减后增的曲线关系。

1.3 研发支出对企业绩效呈现滞后性关系

周艳、曾静[8]以在2002年—2009年沪深上市，连续披露研发支出信息的企业为研究样本。实证研究发现，研发费用投入、研发人员投入与企业利润呈正向相关，并且均存在滞后效应。孔庆景[9]、毛德凤、李静等[10]在各自的实证研究中均发现，研发投入能够促进企业营业利润率的增长，并且这种促进作用具有一定的滞后性。

2 研究设计

2.1 研究假设

研发投入强度的强弱对企业有着不同程度的竞争优势，企业的研发能力决定了企业的核心竞争能力。当企业研发出新的产品，可以为企业带来极大的竞争优势，这些优势可以为企业带来产品的不可替代性，起到降低企业成本，提高企业利润的作用，从而促进企业在市场中占据举足轻重的位置，提高企业绩效。所以，针对上述的研究基础和理论基础，提出以下假设：

假设1：研发投入强度与企业绩效呈正相关关系。

假设2：研发投入强度对企业绩效的影响具有滞后性。

2.2 样本选择与数据来源

本文所选择的研究样本数据，主要是在创业板上市的酒精及饮料酒制造业企业，共有34 家公司，在剔除了ST 股和财务数据不完整的创业板上市公司后，共选择23 家2015年至2017年公司的财务数据为研究样本进行实证分析。

2.3 变量设计（见表1）

2.3.1 解释变量

研发投入强度（RDI）是衡量企业创新能力的核心指标，用来表示企业对科技创新活动的重视程度,所以在相关研究中，大多数学者都选取研发投入强度为解释变量。因此，本文也选取研发投入强度为解释变量。研发投入强度的计算有3 种方法：研发支出/销售收入、研发支出/总资产、研发支出/权益市场价值。根据本文模型的建设需要，选取研发支出与销售收入的比值来表示研发投入强度，其具体表达公式如下：

2.3.2 被解释变量

本文中的被解释变量是企业绩效，企业绩效是指一定经营期间企业的经营效益和经营者业绩。主要有两种评价指标：一是财务绩效指标，二是市场绩效指标。但是，由于我国资本市场的不完善，市场绩效指标难以体现企业价值。所以，本文选取财务绩效指标来反映企业绩效。

净资产报酬率（ROE）作为杜邦分析法体系中综合性最强，最具代表性的指标，它是反映企业所有者投资回报的重要指标，也是反映企业盈利能力的核心指标。因此，选取该指标代替企业绩效作为被解释变量，具体表达公式如下：

2.3.3 控制变量

为了确保本文研究的技术革新与企业绩效关系的全面性和准确性，在进行回归模型时，还应该选取可能会影响企业价值的因素作为控制变量。

（1）企业规模（SIZE）

企业规模指对企业生产、经营等范围的划型。企业规模的大小在一定程度上对企业价值具有不可缺少的影响，为此，在变量中引入企业规模作为控制变量，以控制其对研究结果的影响。其表达公式如下：

（2）资产负债率（LEV）

资产负债率是用以衡量企业利用债权人提供资金进行经营活动的能力，以及反映债权人发放贷款的安全程度的指标，它可以反映公司的债务水平，也可以反映企业财务结构的合理性和偿还债务的安全性，资产负债比率表示为年末负债总额除以年末资产总额的百分比，具体公式如下：

（3）成长性（GROWTH）

成长性是衡量一个企业发展速度的重要指标，代表着企业未来的发展和成长潜力，因此，企业的成长性对本次的研究也有着不可缺少的影响，所以引入成长性作为控制变量，并且选取营业收入增长率来表示，具体表示公式如下：

2.4 模型构建

表1 变量定义表

相关性分析是分析两个或者多个相关变量，由此来衡量这些变量之间的密切程度。多个相关性的元素之间必须存在某种联系或概率才能够对其进行相关性分析。在以往的相关性实证性研究中，大部分的学者都会采用多元回归分析方法来进行实证研究，因此本文在借鉴前人研究成果的前提下，根据上述研发投入强度与相关指标的假设模型。建立以下模型：

在模型中，α 是回归方程的截距项，β 是各项变量的回归系数，ε 为残差项，Y 为被解释变量，及本文中的净资产报酬率，i 表示样本企业，t 表示样本企业所属的年份。

3 实证分析

3.1 描述性统计分析

本文通过对样本企业整理的数据，运用spss22.0 分析系统，得出描述性统计结果，具体见表2样本描述性统计分析表。

从表2可以看出，研发投入强度2015年至2017年的极大值为5.27 %，极小值为0.05 %，平均值为1.15225 %，标准偏差为1.205765，说明在样本企业中，不同的企业之间的研发投入强度水平差距较大，而且企业从2015年到2017年不仅极大值从5.27%降到了3.52%，平均值和标准偏差也都有所降低，表明了样本企业不仅对研发投入的重视程度不够，还有递减的趋势。净资产报酬率极小值都是正数，但是之间的离散程度也很大，说明企业虽然都可以利用企业自有资产获得利润，但是各自企业的自有资产获利能力不尽相同。从各项指标的极大值极小值可以看出，极大值与极小值之间的差距相对较大，尤其是成长性指标。

3.2 相关性检验

根据研究的需要，对上述的相关变量的数据进行相关性检验，具体相关性分析检验结果见表3。

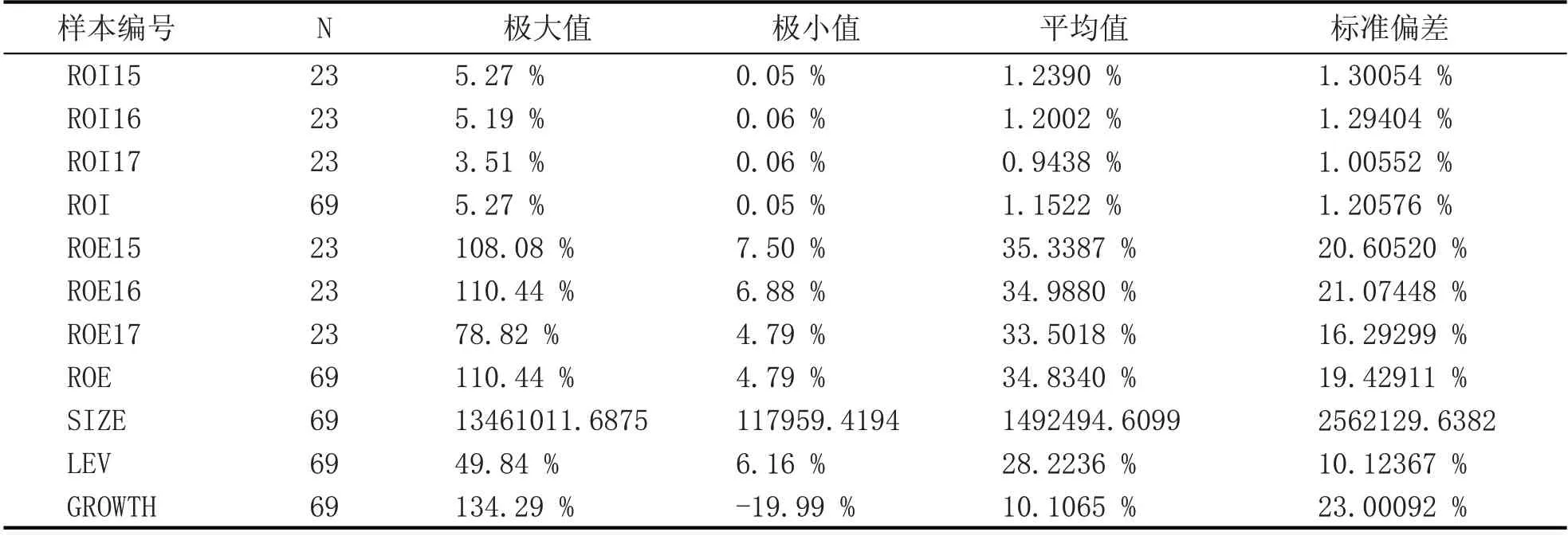
表2 样本描述性统计分析表

表3 变量相关性分析表

从表3 变量分析表中可以看出，研发支出与净资产报酬率之间的相关性为0.116，虽没有通过显著性水平，但是可以初步判断出研发支出与企业绩效呈正相关关系，也就是企业的研发投入强度越大，企业绩效越高，即表明企业技术革新可以提高企业绩效。由于相关性分析的结果仅仅是变量之间的相关关系，未考虑其他相关的变量的影响，具体是否显著正相关还需进一步结合回归分析进行检验才能最终判定。还可以通过表4 初步判断变量之间是否共线，如果存在共线问题，会影响回归分析的效果，可能使得回归结果不具有统计学意义，一般解释变量的相关系数大于0.8，表明会产生共线的可能性。此次相关性分析表中极大值为0.737，小于0.8，可以判断此次的研究回归结果不存在共线问题。

3.3 回归分析

根据变量相关性分析表的内容，可以初步判断企业技术革新与企业绩效呈正相关关系，但是具体的显著性和滞后性还需要运用回归分析进行进一步检验。

（1）企业研发投入强度与当期的企业绩效的回归分析（表4—表6）

由4 表—表6 可知，R 平方反映的是因变量的全部变异能通过回归关系被自变量解释的比例，数值为0.038，说明所建的模型具有一定的拟合度，有一定的解释能力；D—W 值又称为杜宾瓦尔逊值，为0.540，小于2，表明模型的残差项之间不存在自相关，VIF 值是指方差膨胀因子，取值范围大于等于1，VIF 值越大，变量之间的多重共线性就越严重，从回归模型系数表中可以看出，VIF 值都大于1，远小于10，表明自变量之间的相关性对回归模型影响较小，不存在多重共线性问题。可以看出，回归模型试验具有统计学意义，具有一定的参考价值。

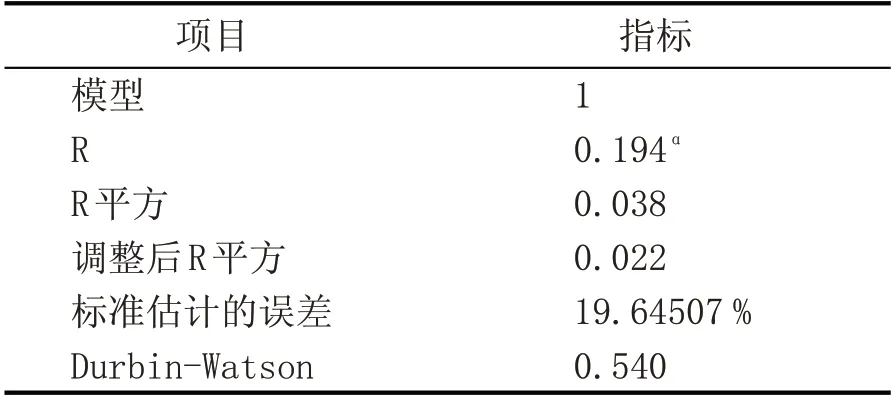
表4 2015年—2017年研发投入强度与企业绩效的模型汇总表b

表5 2015年—2017年研发投入强度与企业绩效的方差分析表b

回归结果显示，回归模型中的F 值为3.628，对应的P 值为0.004，显著性水平小于0.05，表明当期的研发投入强度对企业绩效的影响是显著的。回归系数与相关系数之间的关系呈正相关关系，所以回归系数为1.538，表明研发投入强度与企业绩效呈显著正相关关系，所以假设1 研发投入强度与企业绩效呈正相关关系成立。

（2）企业研发投入强度与滞后期的企业绩效的回归分析

回归结果如表7 所示，企业技术革新与企业绩效的回归系数分别为0.941、1.500和3.396。说明企业技术革新与企业绩效存在正相关关系，并且三期的数值呈逐渐上升的趋势，它表明企业技术革新对企业绩效的作用有一定的滞后性，其作用在不断上升。因此，假设2 研发投入强度对企业绩效的影响具有滞后性成立。

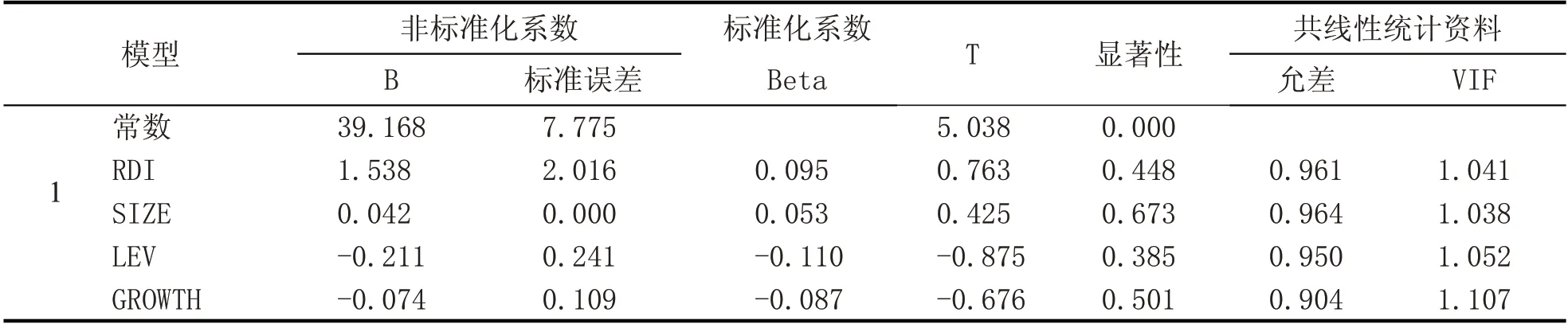
表6 2015年—2017年研发投入强度与企业绩效的回归模型系数表a

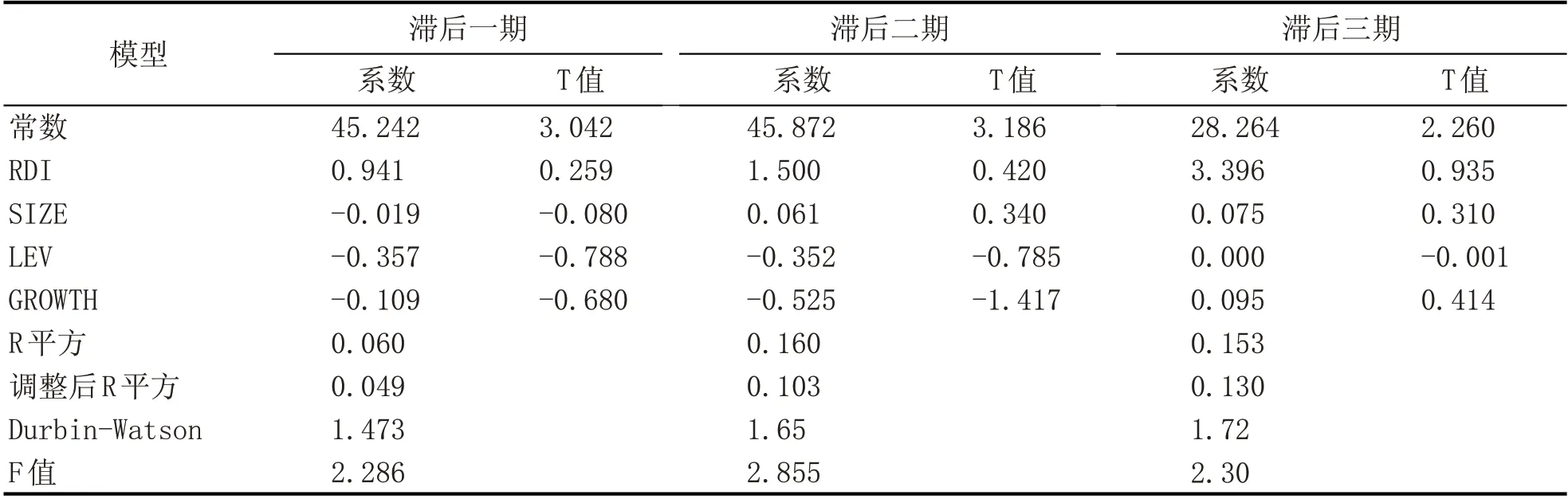
表7 研发投入强度与企业绩效的回归分析表

4 研究结论

本研究以在创业板上市的23 家酒精及饮料酒制造业为研究对象，提出假设，运用多元回归模型进行实证分析，探讨创业板酒精及饮料酒制造业研发投入与企业绩效之间的关系。根据实证分析结果，得出以下结论：

（1）样本公司的研发投入强度在逐年下降，同时企业间研发投入强度不均衡。从前文的描述性分析可以看出，研发投入强度的各年度均值都在1%左右，而且研发投入强度在逐年递减，这表明样本公司的研发水平在逐步下降，竞争优势日益落后。同时，研发投入的标准差数值较大，反映出样本企业之间研发投入水平存在较大的差距，部分企业的研发意识缺乏，存在投入不足现象。对此，企业应当加强并规划企业研发投入强度的力度，合理的，有计划的开展积极有效的研发投入活动。

（2）研发投入强度与企业绩效呈正相关关系。企业的研发投入强度能够提升企业盈利能力，促进企业绩效。即企业可以通过增强研发活动来提高市场竞争力和企业经营绩效。具有滞后性，回归系数在逐年增加，表明企业研发投入强度对企业绩效的影响不仅仅表现为当期的正向促进，也表现出对后期的企业绩效有促进作用，且作用在不断增强。基于此，企业应当提高企业技术革新研发效率，快速回笼资金，降低企业负担，保持企业的优势地位。

所以，希望通过此次的实证研究来引起企业经营者对技术革新的重视，由此来激励企业开展积极有效的技术革新活动，构建企业自身的核心竞争力，提高企业绩效。