道路圆形竖曲线严密计算公式

孙现申 岳魁

（1.郑州工业应用技术学院 建筑工程学院，河南 郑州 451150；2.方宇勘测有限公司，河南 郑州 450000）

道路上、下坡的光滑连接常由圆曲线完成，该曲线的高程计算在一般教材中总是用近似方法，在一般情况下这不影响道路的施工精度。但道路建筑复杂度和施工精度要求的提高让竖曲线严密计算成为必要，计算技术的迅速发展和普及，又使一般的数学计算很容易实现，所以在教学和生产中，竖曲线计算应采用严密公式。

图1 道路圆形竖曲线

图1 表示了道路圆形竖曲线的6 种不同类型，其中，凹型竖曲线（i2＞i1）分为3 类：一类i1＜0、i2＞0，如图1（a）所示；二类i1＞0、i2＞0，如图1（b）所示；三类i1＜0、i2＜0，如图1（c）所示。凸型竖曲线（i1＞i2）也分为3 类：一类i1＞0、i2＜0，如图1（d）所示；二类i1＞0、i2＞0，如图1（e）所示；三类i1＜0、i2＜0，如图1（f）所示。为看图清楚起见，对图1 进行了很大的夸张表示。

在图1 中，已知变坡点C的里程CC和高程HC、第1 坡度i1、第2 坡度i2、圆形竖曲线的半径R。记圆心为O，第1 切点（曲头）为A，第2 切点（曲尾）为B，曲线中点为M。根据已知，依次可以算得：

线型判断符：

当s＞0 时，圆形竖曲线为凹曲线；当s＜0 时，圆形竖曲线为凸曲线。

第1、2 倾角，亦即圆形竖曲线两切线与水平面的夹角：

倾角增量，亦即圆形竖曲线两切线的夹角：

切线长：

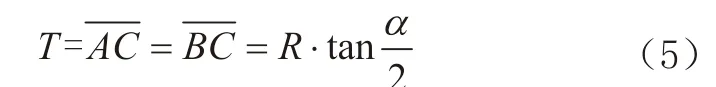
外矢距：

第1、2 切点（曲头、曲尾）A、B的里程：

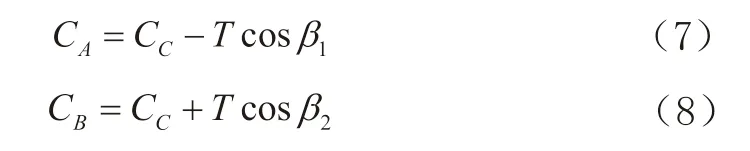
第1、2 切点（曲头、曲尾）A、B的高程：

圆心O的里程，由A点推算，可得：

或由B点推算，可得：

圆心O的高程，由A点推算，可得：

将公式（9）代入公式（13），可得：

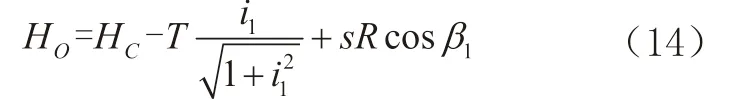
或由B点推算，可得：

将公式（10）代入公式（15），可得：

由上，可得在如图1 所示x-H坐标系中，圆形竖曲线方程为：

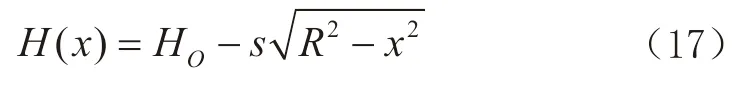
至此，如果知道某点与O点的里程差，就可以用公式（17）计算出该点的精确高程。曲线另外的特征点的计算罗列如下。

曲线中点M是直线OC的分割点，故其里程与高程可由下式给出：

过C点铅垂线与曲线交点的高程：

过O点铅垂线与曲线交点，有文献称为最值点，也就是凹曲线的最低点，或凸曲线的最高点，其里程即CO，其高程由公式（17）可得：

具体的圆形竖曲线计算并不需要上述所有的公式。必要的公式依次为公式（1）～（8）、（11）、（13）、（17）、（18），其余的公式可用于检核计算。

依上述过程和公式，使用True BASIC 算法语言编程，进行了多算例验证，下面是其中一例的输出结果：

表1 道路圆形竖曲线元素计算结果

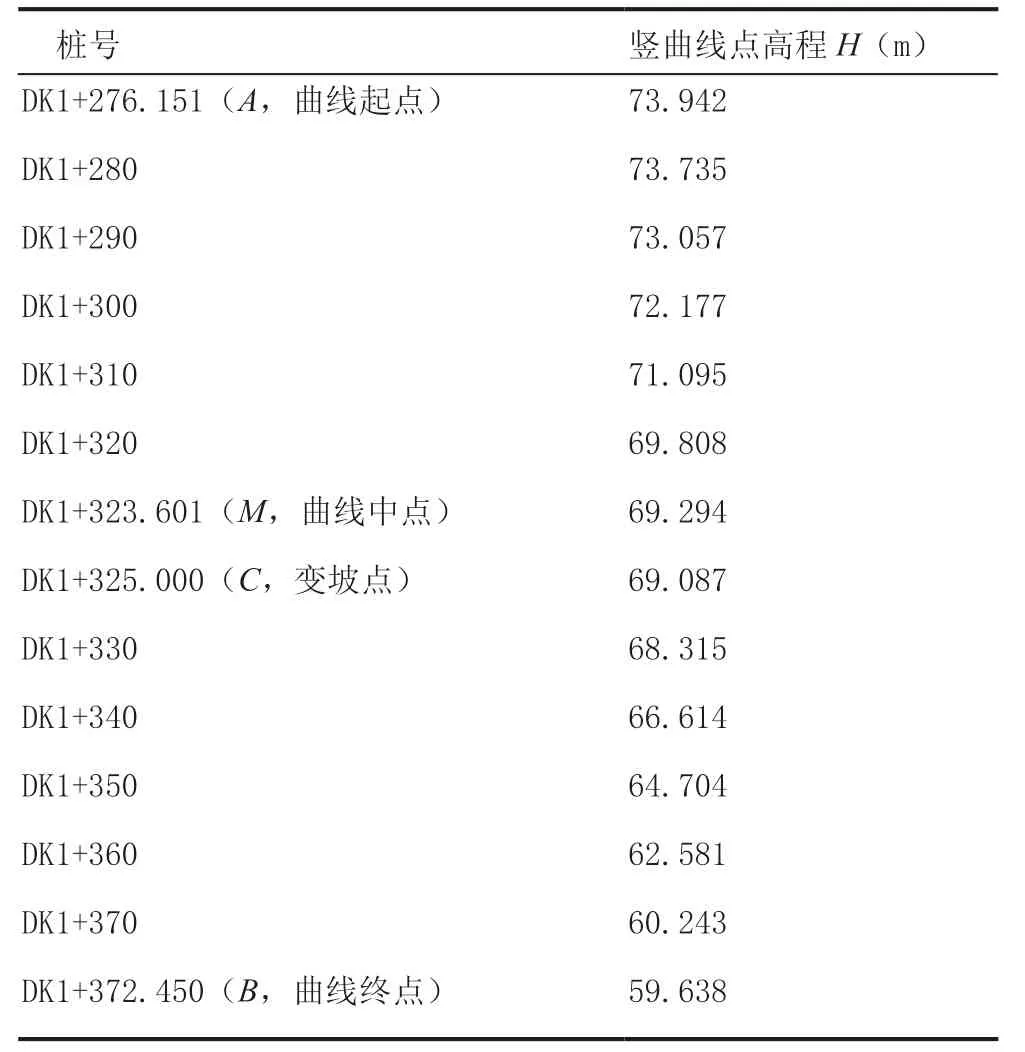
表2 道路圆形竖曲线高程计算结果

关于道路圆形竖曲线的严密计算公式，已有若干文献报道。比较而言，本文给出的计算公式，突出优点在于将各种类型的圆形竖曲线统一在一个计算模型中，而不必在每次计算前先判断圆形竖曲线的类型，然后再选择相应的公式。