航天器降维姿态-轨道一体化控制算法
张恒浩,刘 岱,唐庆博,郑正路,张 霞
(中国运载火箭技术研究院研究发展中心,北京,100076)
0 引 言
航天器控制系统主要负责航天器的姿态控制和飞行轨道控制[1~3],当航天器控制自身姿态的控制系统在单轴方向上发生故障无法正常工作时,会影响航天器的姿态稳定性,并影响航天器轨道飞行,从而导致空间任务失败[4]。研究表明,航天器姿态控制故障是空间任务失败的主要原因之一,如何有效抑制航天器姿态控制故障,提升航天器在轨工作稳定性是现阶段工程研究的热点问题[5~8]。
传统的工程解决方法是在航天器姿态控制系统上增加冗余控制系统[9],当航天器姿态控制系统出现故障无法在单轴方向输出控制力矩时,启动冗余控制系统对航天器进行姿态控制[10]。该方法虽然可以解决航天器姿态控制失效问题,但是在实际应用中冗余控制系统占用了有限的有效载荷质量[11],同时冗余控制系统使得整个航天器控制系统结构复杂化,也降低了控制系统的稳定性[12]。
针对上述问题,提出一种航天器降维姿态-轨道一体化控制方法,设计航天器降维姿态稳定控制器,使用两轴方向控制实现对航天器三轴全维姿态的渐近稳定控制,并给出控制器算法渐近稳定的证明过程;同时设计耦合轨道控制的自适应滑模变结构控制器,在姿态控制单轴失效情况下确保轨道计算渐近稳定,给出轨道控制适应滑模变结构控制器渐近稳定算法的证明。仿真证明,该算法可以将单轴姿态控制失效的航天器自动调整为渐近稳定状态,不再通过冗余控制即可使航天器自行调整到稳定状态,降低了设计成本和控制系统的复杂结构,计算结果满足工程精度要求。
1 一体化控制算法设计
设航天器的本体坐标系为OXYZ,其中X轴指向航天器头部方向为正,Y轴为航天器纵向对称面内垂直于X轴方向,指向航天器上方为正,X,Y,Z轴根据右手定则确定Z轴[13,14]。根据应用背景,设航天器在X轴方向上的姿态控制失效,无法在 X轴方向上输出控制力矩。
设航天器相对于地球的运动学方程为



降维姿态-轨道一体化控制算法对本体坐标系单轴姿控失效的航天器进行控制时,目的是让航天器的姿态角度和轨道位置的相关参数在控制过程中逐渐收敛到工程应用要求的误差以内[20,21]。
1.1 降维姿态控制设计
航天器全维姿态控制方程为

根据应用背景,控制系统对航天器 X轴方向上的姿态控制失效,无法输出控制力矩。此时航天器的全维姿态控制变为降维姿态控制。式(4)表示的全维姿态控制方程变为如下式所示的降维姿态控制方程:

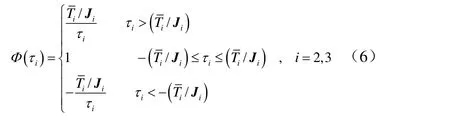








对降维姿态控制器进行渐近稳定控制:
设降维姿态控制器的Lyapunov函数为

对式(15)进行时间求导:


1.2 轨道耦合控制设计
姿态控制发生问题时,会通过耦合关系影响轨道控制。通过降维姿态控制器解决航天器姿态控制失效问题后,还需要设计耦合轨道控制器,消除由于姿态控制失效而对轨道控制的干扰。
全维输入控制力的控制器如下式:



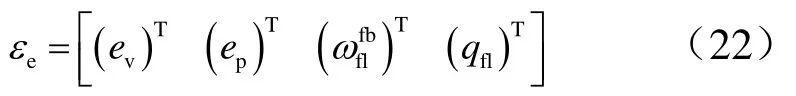
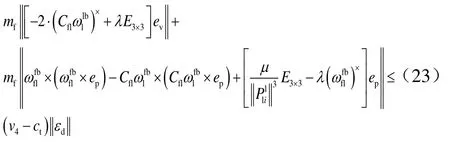
因此设计的轨道控制器采用滑模自适应控制。




2 仿真验证
以美国NASA的OEDIPUS-a任务中执行工作任务的卫星为仿真对象,验证本文提出的降维姿态-轨道一体化控制算法的有效性。
设卫星在工作中控制系统能够提供的最大控制力为20 N,能够提供的最大控制力矩为1 N·m。X,Y,Z轴的转动惯量标定参数均为0.2,降维姿态控制器式(13)引入的计算参数,和的初始值分别为0.01,0.001和0.001。轨道方向标定参数矩阵为diag [ 5, 5, 5 ]。轨道控制器式(24)中,引入的干扰初始值为0.001,自适应调节律,和分别为 10-3,10-4和 10-5,值设为5。
验证降维姿态控制器渐近稳定的Lyapunov函数式(15)中,参数和的值均为0.02。验证轨道控制器渐近稳定的Lyapunov函数式(27)中,参数,和的值均为10-5。
当卫星在本体坐标系OXYZ中沿X轴方向的姿态控制失效时,采用以式(13)和式(24)组成的降维姿态-轨道一体化控制器对卫星进行姿态和轨道的渐近稳定控制。
仿真计算过程中的轨道位置误差在地心赤道惯性坐标系O1X1Y1Z1下计算,该坐标系原点O1在地心,O1X1轴沿着地球赤道平面与黄道面的交线指向春分点,O1Y1轴指向地球北极,O1Z1轴与 O1X1轴和 O1Y1轴构成右手坐标系。
仿真计算开始时间为卫星沿 X轴方向的姿态控制失效时开始,计算时间3000 s。图1~ 3显示的是失效卫星在降维算法控制下解算得到的3个姿态角方向的误差值。图4~ 6显示的是卫星轨道计算误差在地心赤道惯性坐标系中沿 O1X1轴、O1Y1轴和 O1Z1轴的误差。要求卫星轨道在3个坐标轴方向分别产生的误差均不大于30 m。

图1 滚转角计算误差Fig.1 Roll Angle’s Error

图2 偏航角计算误差Fig.2 Yaw Angle’s Error
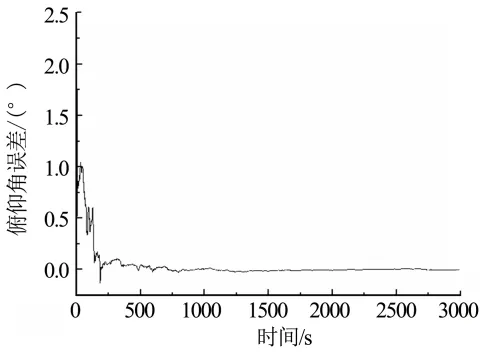
图3 俯仰角计算误差Fig.3 Pitch’s Error

图4 O1X1轴方向计算误差Fig.4 Positional Error of O1X1

图5 O1Y1轴方向计算误差Fig.5 Positional Error of O1Y1

图6 O1Z1轴方向计算误差Fig.6 Positional Error of O1Z1
从仿真结果看,当卫星控制系统在沿X轴方向的姿态控制失效时,卫星姿态角在初始阶段有一个较大的干扰出现,通过降维控制算法实现姿态角渐近稳定控制,俯仰角和偏航角误差逐渐趋向于零,滚转角误差的变化被控制在一个较小范围内变化。由于姿态和轨道计算有耦合关系,因此当沿X轴方向的姿态控制失效时,卫星轨道计算也会出现误差。由于在姿态角渐近稳定控制过程中轨道计算产生了一定的误差。降维耦合控制算法可将轨道算法保持在一个工程可接受的范围内,此时卫星经过降维姿态-轨道一体化控制算法进行渐近稳定控制后仍能正常工作。
3 结 论
针对航天器控制系统在单轴方向上失效问题,提出了一种降维姿态-轨道一体化控制算法。设计降维姿态稳定控制器,使用两轴方向控制实现对航天器三轴全维姿态的渐近稳定控制;同时设计耦合轨道控制的自适应滑模变结构控制器,将轨道计算产生的误差控制在允许范围内。给出降维姿态-轨道一体化控制算法渐近稳定控制的证明过程。仿真结果证明,当航天器控制系统在单轴方向上失效时,该算法可以对航天器姿态角和飞行轨道进行渐近稳定控制,保证其正常运行。

