ＱＢＡＳＩＣ与高中数学《程序语句》章整合的研究

孔宪懿 石辉玲

【摘 要】信息技术与数学课程整合有效整合是新课改的重要特征，而算法语句的教学现状令人堪忧。原因较多：有学生方面的，更多的是教师的教法明显落后于时代科技的发展。本项工作的创新点就在于通过对软件QBASIC的另类实用，调用操作，人机对话，指导学生的研究性学习。关键点就是教师的可操作性强，简单实用。

【关键词】整合策略;微调测试;研究性学习;模拟训练;上机操作

【中图分类号】G623.5       【文獻标识码】A

【文章编号】2095-3089（2019）23-0040-01

一、人教A版《必修三算法初步》现状分析：

在新课标高中数学教材中，提出了信息技术与数学课程整合有效整合的策略，在必修三中设置了算法的内容。算法是计算机科学的理论核心，赋值语句、条件语句、循环语句等计算机语言，实际上是数学语言的“机器化”，它们是信息技术课程和“数学课程”的共同部分，在实际教学中加强两门课程之间的合作，是十分重要的。

课标要求学生通过模仿、操作、探索，经历通过设计程序框图表达解决问题的过程，但在将框图转化为语句之后，学生只能机械进行转化，能否运行下去，结果是什么？学生不知道。数学教师对此也是避而不谈，甚至有些学校的这部分内容让学生自学，或者让信息技术教师教这部分内容，教练就显得脱节。这些都会影响学生的未来发展。21世纪是信息化的世界，很多高中学生往往就输到了起跑线上，造成到了大学里都对上机操作、编程望而生畏。

对此现象，笔者采用QBASIC软件来突破这个难题，采用类似调用程序，“傻瓜操作”的方式来进行，数学教师即便是从未接触过该软件都可以很方便的进行验证。

二、软件简介

1.QBASIC语言的基本知识。

（1）QBASIC语言的基本特点;

常量、变量、字符串、算术表达式的概念;

数的表式方法及范围;

语句的基本格式;

顺序、选择、循环结构的程序设计;

程序设计的基本步骤。

（2）QBASIC语句：

LET  INPUT  PRINT  END  IF   FOR    DO WHILE  REM

（3）算术运算符、关系运算符与逻辑运算符：

+、—、*、/、＼、MOD、^

=、>、<、>=、<=、< >

AND、OR、NOT

（4）流程图的基本符号;流程图的作用。

（5）循环语句。

循环变量、循环体、循环初值、循环终值、步长的概念;循环语句的基本格式。

2.QBASIC的进入。

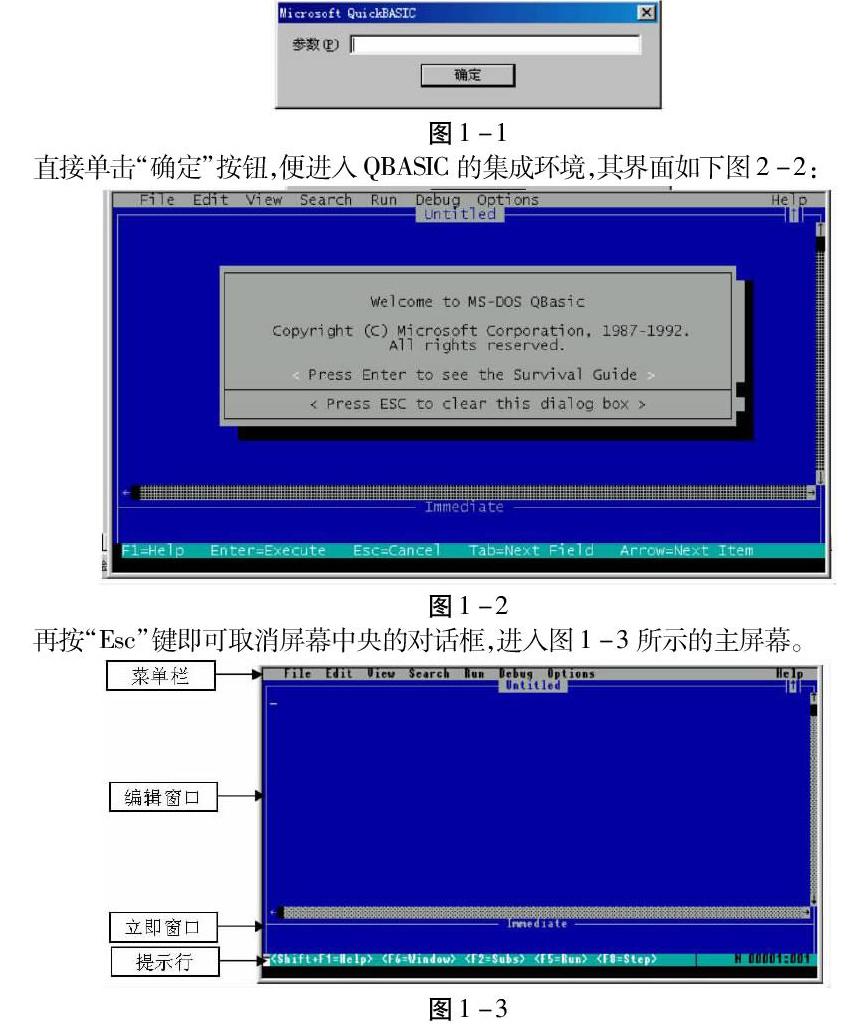
用QBASIC语言编写程序，首先要进入QBASIC集成环境。QBASIC主要由QBASIC.EXE和QBASIC.HLP两个文件组成，按照教师的要求进入指定的位置，运行QBASIC.EXE后，屏幕上会出现一个如图1-1的对话框：

直接单击“确定”按钮，便进入QBASIC的集成环境，其界面如下图2-2：

再按“Esc”键即可取消屏幕中央的对话框，进入图1-3所示的主屏幕。

三、具体实施的方法及创新之处

1.将必修三算法语句中出现的所有例题、习题的源程序设计出来，复制到程序的根目录下。教师只需简单调用程序即可用到平日的教学之中。

2.引导学生有效利用利用QBASIC软件，进行基本语句的计算机语言的验证，初步实现人机对话。

例1.编写程序，计算一个学生数学、语文、英语三门课的平均成绩。

INPUT “数学=”;a

INPUT “语文=”;b

INPUT “英语=”;c

y=（a+b+c）/3

PRINT “The average=”;y

END

3.解决一些最初步的数学应用问题，激发学生的学习兴趣，动力。为以后学习更高等的计算机语言做准备。

例2、编写程序，使得任意输入的3个整数按从大到小的顺序输出。

INPUT “a，b，c =”;a，b，c

IF  b>a  THEN

t=a

a=b

b=t

END IF

IF  c>a  THEN

t=a

a=c

c=t

END IF

IF  c>b  THEN

t=b

b=c

c=t

END IF

PRINT a，b，c

END

例3 写一个算法程序，计算1+2+3+…+n的值（要求可以输入任意大于1的正自然数）

解：

INPUT “n=”;n

i=1

sum=0

WHILE i<=n

sum=sum+i

i=i+1

WEND

PRINT sum

END

穿插在课堂教学，就更能发挥它的最大功效。

4.进行简单的研究性学习。如：通过QBASIC来进行对精度的检验、初等数论的简单命题的程序设计。

例4.在教材的阅读与思考栏中，讲解了通过割圆术来求圆周率∏，谈到刘徽的“徽率”需要作圆的内接192边形，而祖冲之的“祖率”则需作内接12288边形时，能否设计程序，验证次结论？

将这一问题抛给学生后，很快就解决了：

INPUT “N=”;N

I=6

X=1

S=6*SQR（3）/4

WHILE  I<=N/2

h=SQR（1-（X/2）^2）

S=S+I*x*（1-h）2

X=SQR（（X/2）^2+（1-h）^2）

I=2*I

WEND

PRINT  N

END

运行后：n=192，    3.141032

N=12288，  3.141592 ，令人信服的解决了这一问题。

例5、打印出100-999之间的所有“水仙花数”，所谓“水仙花数”就是本数的值等于本数各数字的立方和。如：153=13+53+33[重点是数字的分离技术]。

FOR I=100  TO  999

A=INT（I/100）

B=INT（（I-A*100）/10）

C=I-A*100-B*10

IF I=A*A*A+B*B*B+C*C*C THEN

PRINT I

END IF

NEXT I

END

6.通过上机操作，完成一些程序框图及语句的逐步验证，体会每一次运行后的结果的由来，并能设计出“人腦模拟计算机”的框图表，详见附录1

参考文献

[1]张淑梅.数学3必修（A版）.北京：人民教育出版社，2007年2月第3版.

[2]李彬.“算法初步”一章中若干问题的探讨.数学通讯，2007年第23期.

[3]王丽艳.增强QBASIC语言的教学效果.考试周刊，2012年第26期.

[4]邓德祥，马恕.QBASIC程序设计教程.北京：清华大学出版社1997年.

作者简介：孔宪懿（1975.10-），男，汉族，甘肃天祝县人，高级教师，教龄22年，甘肃省教学能手，擅长高中课堂教学研究。