覆盖层中混凝土防渗墙的三维河谷效应机制及损伤特性

余 翔，孔宪京，邹德高，周 扬

（1.郑州大学 水利科学与工程学院，河南 郑州 450001；2.大连理工大学 水利工程学院，辽宁 大连 116024；3.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024）

1 研究背景

随着水利水电工程建设广泛、快速、深入地发展，尤其是在我国西部地区，直接在深厚覆盖层上修建大坝已成为不可避免的挑战［1］。对于以深厚覆盖层为地基的大坝，坝体和坝基防渗至关重要。一方面，因沥青混凝土在防渗、施工、环保等方面的优势，沥青混凝土心墙坝非常有竞争力［2］。另一方面，坝基渗漏控制广泛采用混凝土防渗墙［3］。混凝土防渗墙位于坝体下部的三维河谷覆盖层中，其受力条件十分复杂。在大坝填筑和蓄水过程中，防渗墙是否会发生不利变形，墙体是否会出现较大压应力或拉应力等，是备受设计者关注的重大问题。不利的应力状态可引起墙体裂缝，从而形成渗流通道，降低其防渗性能［4］，甚至造成其失效，而且防渗墙所处位置的特殊性造成无法开展后期维护。因此，探明深厚覆盖层中混凝土防渗墙的变形及应力分布规律并合理评估其性能至关重要。

我国西部地区地质条件复杂，不同坝址区的覆盖层河谷形状，如：河谷陡缓、岸坡对称性、宽度及深度等差异显著［5-7］。河谷形状的差异会影响防渗墙的变形及应力分布特征，即河谷效应。因此，开展防渗墙变形及应力分布特征的河谷效应及其产生机制的研究十分必要。目前有关土石坝的数值分析中，针对不同河谷地形条件下、不同荷载作用时坝体、面板或心墙［8-10］应力及变形规律、机制等有较为系统的研究。在深厚覆盖层中混凝土防渗墙方面，虽已开展了大量研究，但主要集中于二维分析［11-15］，不能表达三维河谷效应。郦能惠等［16］结合冶勒工程分析了垂直缝、垫座缝、残渣和槽间缝参数对防渗墙三维应力及变形性状的影响。温续余等［17］采用三维有限元法研究了面板坝坝基防渗墙与连接板的连接方式对墙体变形与应力的影响。潘迎等［7］以某沥青混凝土心墙堆石坝为工程背景，研究了宽河谷和窄河谷两种情况下防渗墙竖向压应力的分布特征。余翔等［18］分析了不同时段覆盖层中防渗墙的变形规律、应力分布规律及拉应力产生演化机理。温立峰［19］从统计的角度分析混凝土面板堆石坝覆盖层地基中混凝土防渗墙变形、应力和拉裂特性。目前有关防渗墙河谷效应的研究成果不多，且主要分析墙体变形及应力值的大小，内容单一。此外，目前防渗墙普遍采用线弹性模型分析，数值计算的应力会超过材料强度［19-21］，这与实际不符，且通常认为超过强度即为破坏，无法合理评估防渗墙的性能。塑性损伤模型［22］可以直接获得混凝土防渗体损伤程度，为定量评价提供了可能。因此，开展基于塑性损伤模型的防渗墙数值分析具有重要意义。

本文通过对深厚覆盖层上的沥青混凝土心墙坝进行系统的三维非线性有限元精细数值仿真，深入研究不同覆盖层河谷形状条件，即不同河谷坡度、河谷岸坡对称性、河谷底宽及河谷深度时，防渗墙的变形模式及应力分布空间特征，分析防渗墙的三维河谷效应机制；并结合混凝土塑性损伤模型开展防渗墙的损伤分析，研究墙体损伤特性，讨论防渗墙安全评价分析方法，以期为坝基深厚覆盖层中混凝土防渗墙的设计与施工提供指导。

2 研究方案及有限元模型

2.1 研究方案参考已建沥青混凝土心墙坝［1］，本文采用的大坝几何参数如下：坝高80 m，顶宽10 m，坝坡1∶2.0，坝体河谷坡度为1∶1.0。心墙轴线距坝顶上游侧3 m，其厚度采用渐变式，顶部厚0.5 m，底部厚1.2 m并经2.0 m高的过渡段扩大为2.0 m。心墙两侧设置2 m厚的过渡层。覆盖层采用1.2 m厚的混凝土防渗墙防渗。防渗墙插入上部基座（宽3 m，高2.5 m），与沥青混凝土心墙连接组成防渗系统［23］。

在保持上述大坝几何参数不变的基础上，为研究三维河谷效应对防渗墙的变形及应力分布特性的影响，本文设计了较为系统、精细的计算工况，如表1所示。在研究覆盖层混凝土防渗墙三维河谷效应机制的基础上，针对墙体计算应力超过混凝土材料强度的情况，开展墙体损伤分析，研究墙体损伤-应力特性，并分析防渗墙安全评价分析方法。

表1 计算工况

2.2 有限元模型为精细研究覆盖层中混凝土防渗墙的变形、应力及损伤分布规律，三维有限元网格剖分时，防渗墙的厚度方向采用两层单元模拟，以合理地反映荷载作用下墙体上、下游侧应力状态的差异；同时为准确地描述防渗墙的弯曲变形-应力状态，采用竖向和轴向尺寸均小于2 m的非协调单元［24］模拟防渗墙。

图1为计算工况2-2数值分析时采用的精细网格，其中单元数为534 971个，节点数为549 326个。三维有限元数值模拟时，大坝分层填筑和蓄水共分为34个荷载步，其中16步为由建基面蓄水至坝顶以下3 m处。水位上升时，将水压力施加在防渗系统上、下游面，如图1（c）所示。

图1 数值计算精细网格

3 材料参数及计算方法

3.1 筑坝材料参数Duncan E-B模型在土石坝数值分析中应用最为广泛，且其参数意义明确，本文中土石料与沥青混凝土均采用该模型模拟。材料参数取自实际土石坝工程筑坝材料室内三轴试验的成果［25］，如表2所示，其中，ρd为干密度；φ0、Δφ和c为强度参数；Rf为破坏比；k和n为初始变形模量系数与指数；kur和nur为体积模量系数与指数。

表2 Duncan E-B模型材料参数

受施工方法的影响，防渗墙槽孔底部会残留泥浆与土体混合形成的沉渣［26］，而在防渗墙与覆盖层土体间会形成泥皮［27］。数值分析时，在基岩和防渗墙之间设置沉渣单元，计算参数取覆盖层土体模量参数的2/3［16］。采用Goodman接触面单元模拟泥皮并用Clough-Duncan模型表达其应力变形关系［28］，其中与剪切刚度相关的参数取值为［25］：k1=1400，n=0.65，φ=11.0°，c=0.0kPa，Rf=0.75；而法向刚度根据单元的拉、压应力状态取值。基岩和基座采用线弹性模型，基岩参数为：密度ρ=2400 kg/m3，弹性模量E=9.0 GPa，泊松比v=0.28；基座参数为：密度ρ=2400 kg/m3，弹性模量E=31.0 GPa，泊松比v=0.17。线弹性分析时，防渗墙参数与基座相同。

图2 塑性损伤模型的三维初始屈服面

3.2 混凝土塑性损伤模型及计算方法线弹性分析时，混凝土的计算应力会随荷载增加持续增大，最终远远超过材料强度，这与实际明显不符。当应力达到强度后，混凝土材料会发生应变软化、刚度退化及损伤，并且其具有多轴强度特性［29］。为刻画上述混凝土材料的关键特性，已发展了大量理论上较为先进的材料本构模型，但只有少量模型具有实用性。其中，美国加州伯克利分校Lee和Fenves提出的塑性损伤模型［30］得到国内外广泛认可，已被商业通用软件采用。Lee-Fenves模型的基本理论如下：

该模型采用了总应力与塑性应变的关系表征其应变软化特性：

模量退化随塑性应变呈指数形式增长：

式中：为常数。与总应力相关的损伤因子为：

式中：gÂ为材料完全损伤后的能量耗散密度，与断裂带宽度的特征长度和材料常数断裂能有关。

模型的屈服面采用的是Barcelons屈服面：

用于求解塑性应变的势函数Φ为：

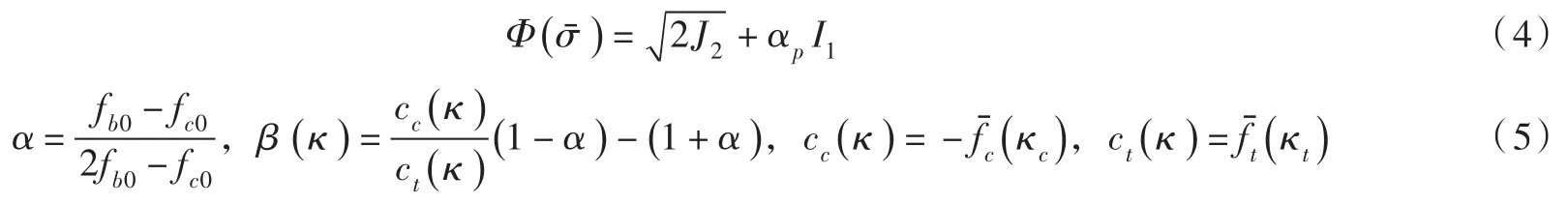
式中：fb0为双轴受压时的屈服强度；I1与J2分别表示有效应力的第一不变量和第二偏应力不变量；αp为表征混凝土体积膨胀特性的参数；为最大有效主应力，为Macaulay bracket函数，表示；a和b常数。当b=0时，该屈服面为Drucker-Prager屈服面；当a=b=0，该屈服面为Mises屈服面。图2为不同屈服函数的三维初始屈服面示意图。

为了将单轴应力状态下的损伤状态变量演化方程拓展到多维应力状态，标量形式的塑性应变率用加权形式的主塑性应变率来表示：

式中：δ为克罗内克函数，和为特征值的最大值和最小值。标量函数为一个满足0≤r≤1的权系数，表示拉主应力在主应力中的比重，反映了当前应力状态的受拉程度。

图3 混凝土单双轴应力-应变关系的数值模拟

Lee-Fenves模型已应用于重大混凝土坝工程的安全评价［31］，但是由于土石坝工程体系十分复杂，且土体材料、接触面等均具有显著的非线性力学特性，计算效率及收敛问题突出，因此该模型在土石坝工程领域应用很少，基本局限于二维分析［32］。为开展混凝土防渗墙的三维损伤分析，采用弹塑性迭代框架和返回映射积分方法将Lee-Fenves塑性损伤模型集成于大连理工大学工程抗震研究所开发的岩土工程非线性有限元分析平台-GEODYNA。

在土石坝工程有限元数值分析时广泛采用土体Duncan-Chang及接触面Clough-Duncan这两个非线性弹性本构模型，然而由于软件计算规模、效率及算法收敛性等限制，大都采中点增量法求解［33］，而这与Lee-Fenves模型的求解框架不符。GEODYNA采用了先进的并行算法，计算效率高，稳定性好，其计算规模已突破了5000万自由度。因此在GEODYNA软件平台的基础上，针对非线性弹性本构模型迭代求解的问题，根据土石坝荷载施加的特点，实现了土石坝体系的自适应增量迭代求解算法。

为验证集成塑性损伤模型的有效性，对已有的混凝土单、双轴试验成果［34］进行数值模拟。由图3可知，数值模拟结果和试验成果十分吻合，且该塑性损伤模型能合理地反映不同应力状态下混凝土材料的关键力学特性。本文损伤分析时混凝土的塑性损伤模型参数参考已有成果［31，35］，其单轴抗拉强度峰值ftmax与初始屈服强度ft0相同取为2.5 MPa，拉断裂能Gt为325 N/m；单轴抗压强度峰值fcmax为30 MPa，单轴初始屈服强度fc0为19.2MPa，压断裂能Gc取为拉的100倍，双轴抗压强度取单轴强度的1.12倍。

4 混凝土防渗墙的河谷效应机制研究

4.1 混凝土防渗墙变形模式为便于分析，将墙轴向坐标归一化为3份，左岸、河谷及右岸部分各1份。图4为满蓄期各工况下防渗墙顶部顺河向位移沿坝轴向的分布。由图表明，满蓄期防渗墙变形的模式为中部变形大，两岸变形小，且在岸坡附近有明显弯曲变形。

图4 各方案满蓄期防渗墙顶部水平位移

对于不同岸坡坡度工况（图4（a））：随坡度变缓，岸坡对防渗墙的约束作用减弱，河谷中部位移增大；当河谷坡度小于1.0后，随坡度的减小，墙体弯曲较大位置逐渐向岸坡移动；当岸坡较缓后，变形的变化较为平缓，且在岸坡处有减小趋势，最后出现使防渗墙弯曲变形最大的临界坡度。

对于不对称河谷工况（图4（b））：缓坡度侧的岸坡对墙体约束作用弱，最大变形位于该侧。同时，不对称河谷坡度工况的最大变形值处于相应对称河谷陡坡度和缓坡度的最大变形值之间，防渗墙在另一侧的变形规律和对称河谷时一致。

当河谷底宽增大时，防渗墙岸坡部分与河谷中部之间的相互影响减弱，其中部变形明显增大，岸坡部分变形规律一致。当河谷底宽较大时，岸坡位置的防渗墙变形的变化很小，见图4（c）。

对于不同河谷深度工况（图4（d））：随着深度的增大，防渗墙水平位移增大但变形规律基本相同。同时，由于防渗墙岸坡部分的轴线长度逐渐增大，墙体弯曲变形较大位置向岸坡处移动。

4.2 混凝土防渗墙应力分布空间特征竣工期，位于大坝中部的防渗墙主要承受压应力，其中覆盖层负摩阻力引起的压应力占总压力的70%～85%［7，20-21］；满蓄期，混凝土防渗墙在岸坡附近位置会产生明显的弯曲变形，造成墙体下游侧产生拉应力［18，36］。混凝土的抗拉强度较低，易使墙体产生裂缝，对防渗安全十分不利，但是目前相关研究较少。而且已有研究主要关注应力大小，然而其空间特征，如位置、方向等对防渗墙安全评价也十分重要。因此，本文重点研究岸坡附近墙体拉应力分布的空间特征。对于河谷对称情况，仅给出墙体左半部分的分布，其中拉应力为负值。

图5 不同河谷坡度时小主应力分布

4.2.1 河谷坡度效应 图5为满蓄期防渗墙下游侧小主应力分布。同时结合表3可以得出：当河谷坡度较陡时，防渗墙轴向宽度沿高程变化不大，两侧河谷对上部和下部防渗墙的约束作用基本相同，岸坡附近防渗墙拉应力变化较小。随着坡度减缓，墙体上部坝体重力增大，防渗墙压应力峰值明显增大。同时，满蓄期墙顶弯曲变形增大，拉应力峰值的位置至墙顶的距离L逐渐减小；坡度小于1∶3.0后，位置几乎不变（见表3）。

图7为满蓄期防渗墙下游侧拉应力（σ3）在墙体上游面的投影与轴向的特征夹角α（示意见图6）的分布。已有研究表明，由于河谷对防渗墙的约束作用，墙体下游侧拉应力主要由沿墙体轴向和竖向分布的水平向变形引起的轴向和竖向拉应力组成［18］。因防渗墙的轴向更柔，沿轴向分布的水平向变形引起的墙体弯曲程度更大，因而墙体拉应力方向更偏于轴向。

图6 拉应力与轴向夹角α示意

图7 不同河谷坡度时拉应力α角分布

表3 不同分析工况时墙体应力峰值信息

图8 河谷坡度不对称时大主应力分布

图9 河谷坡度不对称时小主应力分布

随着岸坡变缓，防渗墙顺河向变形增大，防渗墙弯曲程度增强，墙体两个方向的弯曲拉应力增大，而竖向拉应力的作用增强明显，拉应力逐渐向竖向偏转，这在防渗墙下部更为突出。同时，上覆坝体重力作用下覆盖层变形引起的压应力随岸坡变缓而逐渐增大。因此，在墙体弯曲变形及覆盖层负摩阻力的综合作用下存在使防渗墙拉应力区峰值达到最大的临界坡度（本文为1∶2.0～1∶3.0），这与上节变形结果一致。

4.2.2 河谷坡度不对称效应 当防渗墙两侧河谷岸坡坡度不同时，缓岸坡对土体的支撑作用更强，因而墙体大主应力峰值位于岸坡较缓一侧，如图8所示。由于岸坡处防渗墙的变形规律与对应对称河谷情况基本相同，因而缓岸坡附近拉应力峰值的位置与对称河谷情况差别不大。

与对称的缓坡度工况相比，防渗墙最大变形减小，缓坡度侧的弯曲程度减弱，该侧拉应力减小，但缓侧的坡度对陡侧拉应力峰值的发展规律影响较大。当缓侧的坡度小于临界坡度时，如工况2-1和工况2-2，弯曲变形增大引起的拉应力小于负摩阻力增大引起的压应力，最终使陡坡度侧的拉应力峰值减小；反之陡侧拉应力峰值显著增大，如工况2-3和工况2-4。如图10所示，由于墙体在缓侧的弯曲变形较大，该位置竖向弯曲变形作用较强，防渗墙在缓坡度侧的拉应力方向与陡侧相比更偏于竖向。

图10 河谷坡度不对称时拉应力α角分布

4.2.3 河谷底宽效应 图11为不同河谷底部宽度时满蓄期防渗墙小主应力分布云图。随河谷底宽的增大，厚度较薄的防渗墙柔性增强，较大的弯曲变形使岸坡附近墙体弯曲程度更为显著，墙体拉应力峰值逐渐增大，且峰值的位置向墙体下部发展，如表3所示。

图12为特征夹角α的分布图。不同底部宽度时，墙体拉应力峰值区的拉应力方向更偏于竖向。当河谷底部很宽时，覆盖层土体对墙体的负摩阻力基本全部发挥且河谷岸坡的支撑作用减弱，墙体竖向压应力增幅不再明显且峰值基本位于墙体底部（图12）。同时，墙底弯曲变形逐渐增大，防渗墙底部出现了局部偏于竖向的拉应力区（图13（c））。

图11 不同河谷底宽时小主应力分布

图12 工况3-4时大主应力分布

图13 不同河谷底宽时拉应力α角分布

4.2.4 河谷深度效应 图14为不同河谷深度时防渗墙的小主应力分布。当河谷深度减小时，防渗墙的柔性随宽高比增大而增大，河谷底部对防渗墙的约束作用相对增强，墙体下部产生了明显偏于竖向的拉应力。当河谷深度增大时，覆盖层土体对墙体的摩阻力增大，对墙体拉应力的发展起一定限制作用，墙体下部拉应力区逐渐消失，见图15。如表3所示，墙体大主应力随深度的增大增幅明显，因而应关注深防渗墙的受压破损的危险性。另外，随防渗墙深度的增大，墙顶弯曲变形增大，拉应力峰值的位置逐渐向墙体上部转移。同时，覆盖层土体的负摩阻力引起的墙体压应力增大，墙体拉应力峰值表现出先增大后减小，因而存在墙体拉应力峰值的临界深度（本文为60～80 m）。

5 混凝土防渗墙的损伤特性研究

图14 不同河谷深度时小主应力分布

图15 不同河谷深度时拉应力α角分布

根据以上系统的防渗墙弹性分析结果，通过研究墙体变形模式及应力分布空间特征，能方便地把握墙体受力-变形-应力规律，揭示墙体的三维河谷效应。但计算结果中，墙体应力峰值（尤其是拉应力）很容易超过混凝土材料强度，而实际上这种现象很难发生。因此，直接用线弹性模型计算的应力结果去评估防渗墙的防渗性能是不合理的。要合理、准确地评价防渗墙安全性，需开展深入研究。工况3-4（防渗墙深80 m，底宽400 m，两岸坡度均为1∶1.0）时，墙体的拉、压应力峰值均超过本文第2节介绍的混凝土强度值。本节以工况3-4为例开展损伤分析，研究墙体损伤-应力规律。

图16为采用塑性损伤模型进行损伤分析获得的墙体大主应力分布。与图12相比，损伤分析获得的大主应力较线弹性分析稍有减小，且超单轴峰值强度（30 MPa）的区域减小。由于塑性损伤模型考虑了三维受压状态下混凝土强度提高的特性，损伤分析获得的墙体压应力仍会超过材料的单轴抗压强度。此时进行墙体安全评价不再根据应力值，而是采用与墙体防渗性直接相关的损伤因子［37］。图17中的压损伤因子代表墙体各位置的损伤程度。可以看出：整个墙体的最大压损伤不大于0.10，属轻微损伤，尽管此时墙体中的最大压应力仍较大，墙体不会发生受压破坏。因此可以认为，覆盖层中混凝土防渗墙的抗压安全裕度较高。

图18为损伤分析获得的满蓄期墙体小主应力分布。与线弹性分析结果图11（c）相比，墙体拉应力峰值和范围明显减小，最大拉应力小于1.0 MPa，且墙顶端部和墙底处于受压状态。图19为损伤分析获得的墙体拉损伤因子分布。可以看出，线弹性分析与损伤分析获取的拉应力区域差别不大，但是由于损伤分析考虑了防渗墙结构局部位置损伤后的墙体应力重分布的特性，拉损伤程度大的位置和线弹性分析获得的拉应力大的位置不同，满蓄期应力状态亦有较大差别。另外，损伤分析的最终状态能够反映防渗墙结构受力过程中每个位置的最不利情况，而线弹性分析仅与当前应力状态相关，因此线弹性分析获得的最终状态结果并不一定最危险。损伤分析获得的墙顶端部和岸坡附近的局部位置拉损伤因子超过0.70，相对比较危险，需加强关注。和抗压安全相比，由于混凝土材料抗拉强度低，三维受力状态下强度可能会进一步降低。因此，应更加关注覆盖层中混凝土防渗墙的抗拉安全性。

图16 损伤分析时的大主应力分布

图17 损伤分析时的压损伤因子分布

图18 损伤分析时的小主应力分布

图19 损伤分析时的拉损伤因子分布

通过对比损伤分析和线弹性分析结果，不难得出：若直接采用基于线弹性分析的计算应力和材料强度评价墙体安全，将会得出墙体大范围破坏的结果，低估防渗墙的安全性。另外，坝基覆盖层中的混凝土防渗墙的基本功能是防渗，而采用线弹性模型计算的应力结果进行安全评价时针对的是结构的承载能力，与防渗墙的功能不符。基于损伤分析的安全评价，可通过损伤因子直接明确墙体各部位的损伤程度，并且损伤因子与混凝土材料不同状态下的防渗性能存在直接联系，应用更加合理和准确。

6 结论

本文通过系统的数值分析，研究了覆盖层中混凝土防渗墙的变形模式及应力分布空间特征，分析了墙体的河谷效应机制及损伤特性，讨论了墙体安全评价分析方法。结论如下：

（1）覆盖层中混凝土防渗墙的变形模式为中部大，两岸小，在岸坡附近有明显弯曲变形，但不同河谷地形的墙体弯曲变形大小及极值位置差别大。在弯曲变形引起的拉应力及负摩阻力引起的压应力的综合作用下，墙体的应力峰值位置、大小和方向等分布特征发生改变。

（2）存在使防渗墙拉应力峰值达到最大的临界坡度和临界深度。本文的临界坡度为1∶2.0～1∶3.0，临界深度为60～80 m。当岸坡不对称且缓侧坡度大于临界坡度时，陡侧拉应力较对称情况时大。随河谷宽度增大，墙体拉应力峰值区向下部转移。应重点关注岸坡不对称、宽深河谷中防渗墙的安全。

（3）混凝土防渗墙拉应力的方向偏向轴向，在应力峰值区与轴向夹角相对较大；随墙体弯曲变形增大，逐渐向竖向偏移。墙体应力分布空间特征的研究对墙体设计（如：配筋方向、位置等）具有重要的指导意义。

（4）覆盖层中混凝土防渗墙压损伤较大部位位于墙体下部，墙顶端部和岸坡附近的拉损伤程度较高。而防渗墙的抗压安全裕度较高，应更关注墙体的抗拉安全性。

（5）基于线弹性分析，能简便地认识防渗墙的受力-变形-应力规律，进而探明关键因素对墙体的影响机制。但是线弹性计算应力与防渗墙的防渗功能难以建立联系，采用材料强度进行安全评价时，会明显低估防渗墙的安全性。基于塑性损伤模型的损伤分析能描述混凝土材料的三维强度特性、应变软化、刚度退化及损伤特性，可以反映结构局部损伤引起的应力重分布特征，最终直接获得墙体各部位的损伤因子。损伤因子与坝基覆盖层中混凝土防渗墙的防渗性能存在直接联系，用于墙体安全评价时更加合理和准确。