基于降雨入渗全过程的非饱和湿润峰模型

徐 旭，席 越，姚文娟

（1.上海大学 土木工程系，上海 200444；2.上海大学 力学与工程科学学院，上海 200444）

1 研究背景

自改革开放以来，中国的城镇化建设进程不断加快。但由于粗放的发展模式，城市自然水文循环过程遭到破坏，从而导致城市内涝灾害的频繁发生［1］。因此，缓解城市管网的排水压力，优化生态环境，最大限度地实现雨水在城市区域的积存、渗透和净化，已成为人类生存需要解决的重大问题［2］。为此，许多学者进行了降雨入渗过程的研究［3-6］，以便充分发挥土壤的蓄水能力，准确预测径流。

目前，具有代表性的降雨入渗计算方法为Mein-Larson降雨入渗模型［7］和数值模拟方法［8-10］。Mein-Larson模型由于基于物理假设且计算简便，从而被广泛使用。但由于该模型采用水平湿润峰假设，假定土壤湿润区均为饱和含水率，土壤入渗过程中的水力传导度取为饱和渗透系数，这会导致土壤蓄水量被高估。从而学者们不断地改进该模型。李宁等［11］引入Van Genuchten水力传导函数，忽略土壤吸力梯度对入渗过程的影响，建立了可以反映低强度降雨条件下非饱和土入渗过程的改进模型。于宁宇等［12］引入Van Genuchten基质吸力模型考虑土壤基质吸力对入渗过程的影响，建立了适用于吸力显著土壤的入渗模型，并且可体现土壤含水率随入渗时间的变化。唐扬等［13］在模型中加入了土壤初始含水率的分布情况对降雨入渗的影响。以上修正模型均采用水平湿润峰假设，而实际入渗过程中土壤水分剖面呈明显的层状分布［14］。由于该假定过于简化，从而限制了模型的计算精度。同时，也会影响降雨入渗过程中各时间节点的确定。

本文参考前人的实验以及数值模拟结果，对降雨入渗全过程进行分段，假设各阶段土壤水分剖面的分布状态，提出修正的湿润峰模型。同时，结合达西定律，引入土体非饱和参数，使修正后的模型可以更加真实地反映实际入渗过程，并且能够更加精确地预测土壤累计入渗量和积水时间。

2 模型建立

降雨入渗按照降雨强度与土壤饱和渗透系数的相对大小主要可分为两类。本文分别针对以下两种降雨条件建立修正模型。

2.1 降雨强度小于土壤饱和渗透系数当降雨强度小于土壤饱和渗透系数时，整个降雨入渗过程为非饱和入渗，所有雨水均渗入土壤，故不产生积水，又可称为无压入渗。设降雨强度为r，土壤入渗率为q，降雨入渗可简化为一维入渗情况，由达西定律可得：

式中：K（θ）为土壤非饱和渗透系数；zf为湿润区浸润深度；h1、h2分别为土壤表层和湿润峰处基质势吸力水头。

降雨入渗初期，土壤中形成的湿润区域不断扩大，其表层含水率及浸润深度同时增加，土壤含水率沿深度方向逐渐减小。王文焰等［15］根据实验结果，假定入渗过程中非饱和区含水率剖面为1/4椭圆曲线。彭振阳等［16］同样采取该假定，结合Richards模型计算结果对Green-Ampt模型进行改进，取得了良好的计算效果。本文同样假设在降雨入渗初期，土壤水分剖面呈椭圆形分布。设土壤表层含水率为θi，初始含水率为θ0，其湿润区平均含水率为：

本文引入Van Genuchten模型［17］，如式（3）、式（4）所示。以湿润区的平均含水率所对应的土壤基质势和非饱和渗透系数等效替代实际的土壤基质势以及非饱和渗透系数。

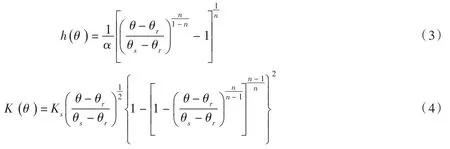
由于降雨强度小于土壤饱和渗透率，其入渗率q等于降雨强度r，将式（2）、式（3）和式（4）带入式（1）中可得：

设降雨历时为T，根据水量守恒定律可知，土壤累计入渗量等于其含水量增量，即得：

将式（6）带入式（5）可消去zf，即得：

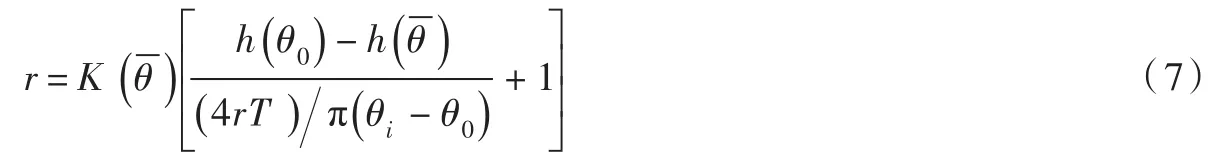
上式即为降雨初期土壤入渗的控制方程，可通过迭代的方法计算出给定T时刻所对应的土壤水分剖面分布。

表层土壤最终的入渗率为表层土体含水率的函数［18］，由式（1）可知其数值上等于表层土壤含水率所对应的非饱和渗透系数。对于恒定雨强的降雨，随着入渗过程的推进，土壤表层含水率逐渐增加至一定值后不再发生变化［19］，将该值称之为临界含水率（θc）。此时，降雨强度与表层土壤的入渗率相等。故临界含水率可由式（8）计算得出。

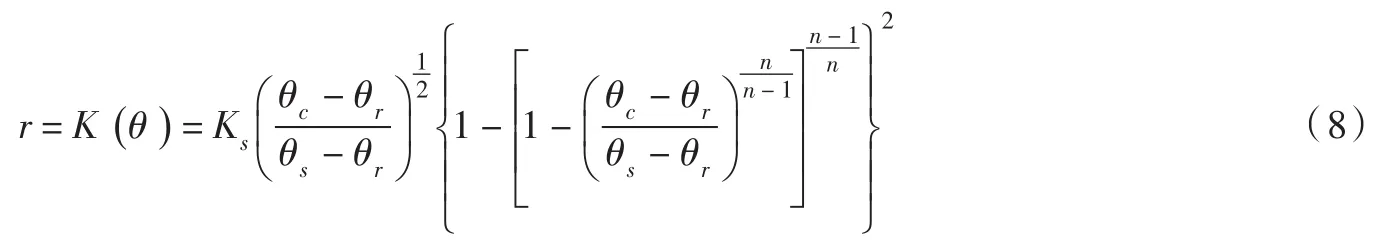
另外，有试验结果显示，在降雨入渗后期，土壤的浸润深度随时间呈线性增长［20］，且土壤过渡层所占总湿润层的比例线性下降［16］。而且根据数值模拟结果可知，对于恒定降雨强度的入渗，过渡层的厚度将逐渐趋于稳定。基于以上原因，本文假设已形成的椭圆形湿润区形状不再发生变化，并称之为无压入渗过渡区，随着入渗进程均速向下推进。过渡区以上的湿润区含水率均为临界含水率，土壤水分剖面开始出现分层现象。

为方便叙述，称出现分层前的阶段为无压入渗过渡阶段，分层后为无压入渗稳定阶段。对于无压入渗稳定阶段，根据水量守恒定律可得：

式中：Tc为土壤表层含水率由初始含水量增长至临界含水率所用的时间，称为临界时间。zfc为过渡区的深度范围。由式（9）可知，在无压入渗稳定阶段土壤湿润区深度随入渗时间线性增长，其变化规律与试验结果相吻合。

设累计入渗量为I，基于以上的假定与推导，累计入渗量可以用下列表达式计算：

2.2 降雨强度大于土壤饱和渗透系数当降雨强度大于土壤饱和渗透系数时，整个入渗过程将经历三个阶段：降雨强度控制入渗阶段，非饱和状态控制入渗阶段和饱和状态控制入渗阶段。

降雨初期土壤的入渗能力大于降雨强度，此时土壤入渗率取决于降雨强度，故称为降雨强度控制入渗阶段。该阶段内所有雨水均渗入土壤，不产生地表径流。与降雨强度小于土壤饱和渗透系数时的无压入渗过渡阶段相同，可同样采用式（7）作为该阶段的控制方程。

由于降雨强度大于饱和渗透系数，表层土壤的渗透系数无法增长至与降雨强度相等，表层土壤的含水率先达到饱和含水率（θs）后保持不变。由式（5）可知，当土壤湿润区平均含水率不变时，随着土壤湿润区深度增加，土壤的入渗率不断减小，导致此后的降雨强度大于土壤的入渗率，部分雨水无法渗入土壤，从而形成地表径流。降雨入渗过程开始进入积水入渗阶段。

在积水入渗初期，土壤的入渗能力小于降雨强度，但大于土壤饱和状态下的入渗率（即饱和渗透系数）。该阶段土壤的入渗率取决于非饱和土的入渗能力。假定该阶段土壤含水率

剖面仍呈椭圆形分布，土壤表层含水率为定值θs，故土壤湿润区的平均含水率为：

由水量守恒定律可得：

将式（5）、式（11）代入式（12），整理可得：

其中，zfp=4·r·T［/π·（θs-θ0）］，为积水点所对应的土壤浸润深度。式（14）即为非饱和状态控制入渗阶段的控制方程。

当土壤入渗能力减小至等于土壤饱和渗透系数时（即q=Ks时），由于此后的入渗速率恒定，与无压入渗稳定阶段类似，故同样假设已形成的椭圆形湿润区形状不再发生变化，称之为积水入渗过渡区，随着入渗进程向下均速推进。过渡区以上的湿润区含水率均为饱和含水率，土壤水分剖面开始出现分层现象。降雨入渗过程开始进入饱和状态控制入渗阶段。根据水量守恒定律可得：

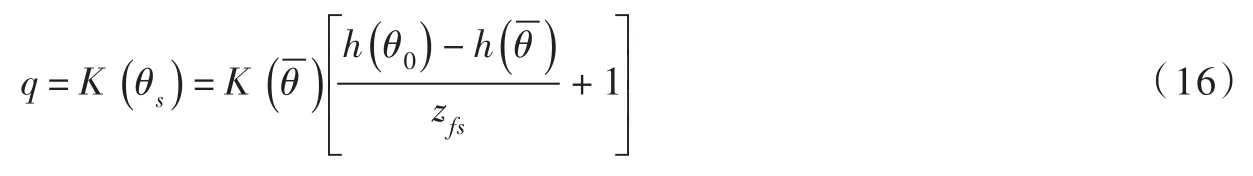
式（15）即为饱和状态控制入渗阶段的控制方程。其中，zfs为积水入渗过渡区的深度范围，可由式（16）计算得出。Ts为达到饱和状态控制入渗阶段所需的时间，可将zfs代入式（14）计算得出。

为方便后文叙述，类比前一种降雨条件下的入渗过程，将积水入渗非饱和状态控制阶段与饱和状态控制阶段称之为积水入渗过渡阶段与稳定阶段。

设累计入渗量为I，基于以上假定与推导，各阶段的累计入渗量可以用下列表达式计算：

3 结果分析与验证

3.1 计算结果分析本节首先利用上节提出的修正模型计算土壤在不同降雨强度下的入渗情况。修正模型的计算流程如图1所示，本文采用Matlab软件实现整个计算过程。计算过程中的土质参数取自文献［13］，土质类型为粉质黏土，考虑土壤含水率沿深度方向均匀分布的情况，不考虑地下水埋深的影响，设土壤初始含水率为0.2。具体水力参数见表1。

表1 土体水力参数

图2为当降雨强度分别为10 mm/h和30 mm/h时，土壤水分剖面在不同时刻的分布情况。两个降雨强度分别对应上节中提到的两种降雨入渗情况。从图中可见，随着入渗时间的增加，土壤的湿润区范围不断扩大。本模型可以反映在降雨入渗过程中，土壤含水率分布沿深度方向并不均匀。地表含水率较高，土体内部含水率随土壤深度逐渐减小。另外，图中可以明显的显示出土壤含水率剖面的分层现象。相较于传统的水平湿润峰假设模型，本模型更符合实际的入渗状况。

不同降雨强度下，土壤表面的含水率随时间的变化趋势如图3所示。降雨初期，土壤的表层含水率呈非线性增加。当入渗持续一段时间后，土壤表层含水率将会逐渐趋于一定值，即临界含水率。当降雨强度小于土壤饱和渗透系数时，临界含水率小于土壤饱和含水率，并且与降雨强度成正比。当降雨强度大于土壤饱和渗透系数时，临界含水率等于土壤饱和含水率。当降雨强度越大，表层土壤达到临界含水率所需的时间越短。

图4为本文提出的修正模型在不同降雨强度下，土壤浸润深度随时间的变化。由图可知，降雨前期，各降雨强度下土壤浸润深度随时间呈非线性增长。降雨后期，土壤浸润深度随时间呈线性增长。对于降雨强度小于土壤饱和渗透系数的入渗过程，降雨强度越大，其增长速率越大。当降雨强度小于土壤饱和渗透系数时，土壤浸润深度曲线在降雨后期基本平行，且其数值相差不大。该结果与实际入渗规律更加接近。

图1 修正模型计算流程图

图2 不同时间不同降雨条件下土壤含水率分布

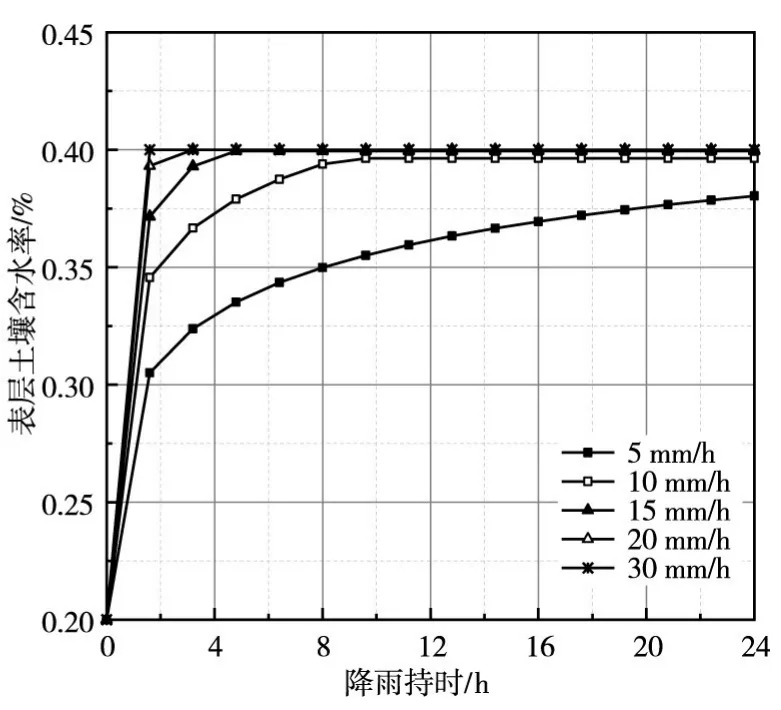
图3 土壤表层含水率随时间的变化

不同降雨强度下土壤的累计入渗量如图5所示。两种降雨条件下，土壤累计入渗量随时间的变化规律有所不同。当降雨强度小于土壤饱和渗透系数时，土壤的累计入渗量呈线性增长，且其增长速率等于降雨强度。当降雨强度大于土壤含水率时，土壤的累计入渗量的增长分为三个阶段。降雨初期呈线性增长，增长速率等于降雨强度。降雨中期呈非线性增长，此时的增长速率由土壤的非饱和性质控制。降雨后期呈线性增长，增长速率等于土壤饱和渗透系数。故从图中可以看出，在降雨后期，当降雨强度为30 mm/h和40 mm/h时，两者的累计入渗量的增长曲线平行。另外，两者的累计入渗量也十分接近，说明对于高强度降雨条件下的降雨入渗，最终的入渗量主要取决于土壤饱和渗透性质。

图4 土壤浸润深度随时间的变化

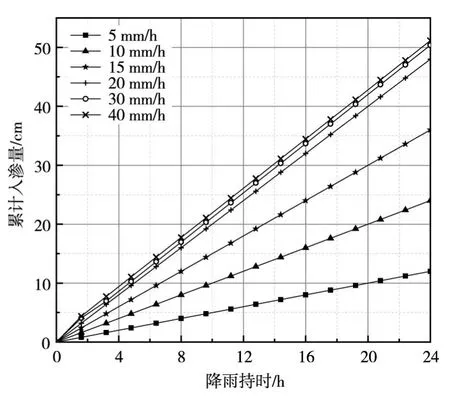
图5 累计入渗量随时间的变化

3.2 模型验证为验证修正模型计算结果的准确性，将修正模型和数值模型的计算结果进行对比。另外，由于Mein-Larson模型为采用“水平湿润峰”假设的经典降雨入渗模型，故将其计算结果加入比较，对本文修正方法的效果进行评价。将传统模型与修正模型计算结果称为累计入渗量的预测值，作为纵轴。将有限元软件的模拟结果称为累计入渗量的计算值，作为横轴。当数据点越靠近对角线，则说明两者吻合愈好。本文选择土壤浸润深度与累计入渗量的计算结果作为验证项目。对于累计入渗量的对比，仅选择降降雨强度大于土壤饱和渗透系数的情况，即降雨强度为30 mm/h和40 mm/h的计算结果。具体对比结果见图6及图7。

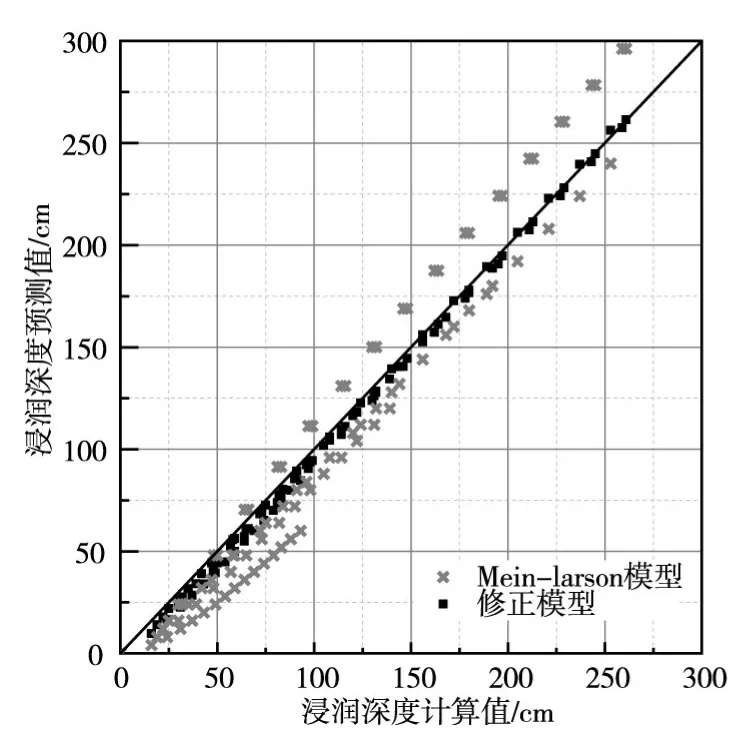
图6 浸润深度对比

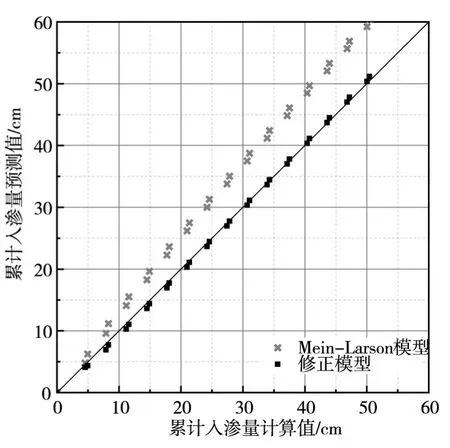
图7 累计入渗量对比

由图6可知，传统模型和修正模型的浸润深度计算值根据降雨强度不同，其相对大小有所差异。当降雨强度小于土壤饱和渗透系数时，由于两种模型入渗量计算值相等，本文所提出的模型考虑了该情况下土壤处于非饱和状态并且含水率分布不均，故修正模型的计算结果大于传统模型的计算结果。

当降雨强度大于土壤饱和渗透系数时，如图7所示，由于本本文模型考虑前期非饱和入渗阶段，故其入渗量计算值小于传统模型计算值，并使其浸润深度计算值将小于传统模型计算值。另外，本文模型的计算结果与模拟结果的最大误差小于5 cm，相对误差均小于5%。根据以上分析结果可知，本文提出的修正模型在传统模型的基础上，修正效果较好，对于计算结果的准确性方面有了很大的提高。

积水时间也是降雨入渗过程的重要指标之一。表2即为不同计算方法所得的积水时间的对比。从表中的数据可以看出，修正模型相较于传统模型更加接近数值解，说明本文的修正模型对于节点的假定合理，当土壤表层含水率达到饱和含水率时开始出现积水。

表2 积水时间的模型解及数值解的比较

为了检验本文提出的模型对于其他类型的土壤的适用性，本文另外选取3组不同土质土壤进行计算，并与有限元结果进行比较。具体土体参数［16，21］见表3。4组土壤的土-水特征曲线如图8所示。

图9即为4种土质在不同降雨强度下，两种计算方法所得的累计入渗量的对比图。虽然图中显示有数据点偏离较大，但实际误差均小于2 cm。砂土相差最大，基本差值范围在1～2 cm之间。粉土与壤土相差范围较小，其范围在0.1～0.5 cm之间。由此表明本文提出的修正模型对于不同土质土壤适应性良好。

综上所述，本文所建立的修正模型假定合理，对于两种降雨入渗情况计算结果的准确性较好，其计算结果满足误差范围，并且更加接近真实的入渗情况。另外，本文模型也可以适用于其他类型的土壤。

表3 土体水力参数

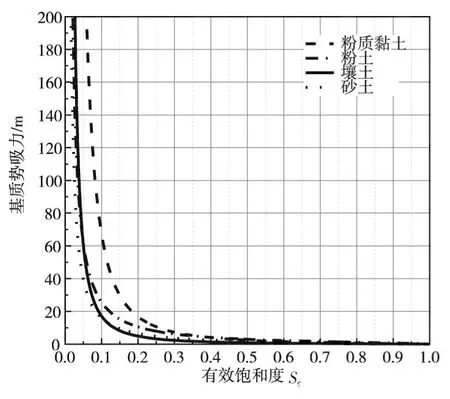
图8 不同土质土壤的土-水特征曲线

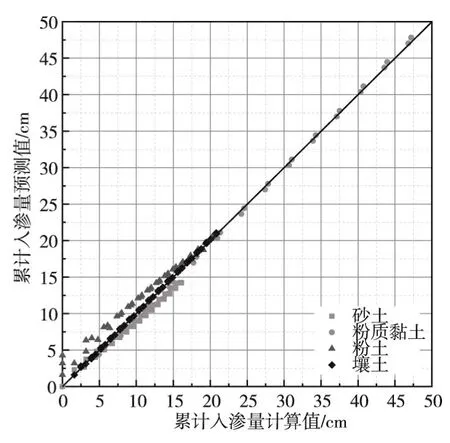
图9 不同类型土的模型解与数值解的对比

4 结论

（1）与现有的入渗模型相比，本文提出的入渗模型符合实际入渗过程中的土壤含水率分布，能够更加真实地体现出土壤表层含水率和浸润深度随时间的变化趋势。

（2）对于降雨强度小于饱和渗透系数和降雨强度大于土壤饱和渗透系数的两种降雨入渗情况，本文模型所得的计算结果与有限元软件模拟结果吻合，明显优于传统模型。

（3）当降雨强度大于土壤饱和渗透系数时，当表层土壤饱和后，即出现积水。土壤累计入渗量最终取决于土壤的饱和渗透性质，降雨强度对其影响有限。

（4）本文明确了降雨入渗过程中各阶段的状态和节点发生时间，与有限元方法相比更加简单，便于计算并且计算效率得到提高，且具有良好的计算精度，因此可以利用本模型对积水时间与土壤蓄水量进行计算和预测。