《皇极历》中的漏刻差分表
曲安京 辛佳岱
(西北大学科学史高等研究院,西安 710127)
刘焯的《皇极历》(公元604年)是中国历史上一部极具创新性的历法,它虽然未获颁行,但是,刘焯在这部历法中创造的分段二次插值算法,对后世历法的编制模式,产生了很大的影响[1]。我们知道,对于历法中的许多计算,为了构造分段的高次插值公式,通常需要预先构造一个(24气的)天文数表,在理想的情形下,这个数表应该是一个完整的差分表。《皇极历》中的夜半漏刻与昏去中星表,就是为了构造相应的分段二次插值公式设计的天文数表。
不过,《皇极历》的这个天文数表,有不少的错讹,严敦杰与陈美东先生对此都有校正,但是,仍然存在不少的问题。主要的原因是,目前的研究者虽然搞清楚了这个天文表的天文意义,但是,对其数学结构均未曾考虑。因此,很难确认已经给出的校勘是否是合适的。本文希望从这个天文表的构造原理入手,重新考察这个问题。
1 问题与原理
《皇极历》收录在《隋书·律历志》卷十八,在1976年中华书局编辑出版的《二十四史》中,严敦杰承担了《隋书·律历志》的校勘,其中对《皇极历》夜半漏刻与昏去中星表的数据给出了8条校勘[2]。陈美东在这个基础上,又给出了8条校勘([3],页47—48)。为了考验前人校勘的准确性,我们需要解释一下《皇极历》中的夜半漏刻与昏去中星的天文意义和数学关系。
为了计算每日昼夜漏刻的长度、每日昏旦时刻太阳到中星的距离,《皇极历》设计了一张24气的夜半漏刻与昏去中星度天文数表。利用这个天文数表,可以构造相应的分段插值公式,以计算每日昼夜漏刻的长度与当日昏旦时刻太阳到中星的距离。所以,讨论这个天文表的构造方法,是一件有意义的工作。为此,我们将《隋书·律历志》中记录的《皇极历》24气的夜半漏刻与昏去中星度的原文数据照录如表1所示。为方便醒目,我们将原文的数字均改为阿拉伯数字。
夜半漏的单位为刻,1刻=100分,例如,谷雨日,夜半漏为“二十刻 三半”,即这一天夜漏刻一半的长度为20.035刻。

由于对称性,除冬至、夏至外,其余各气的数据应该成对出现,彼此相等,为了便于比较,我们将彼此数据应该相等的两气并列一行,分别依次罗列出两气的夜半漏与昏去中星常数。
例如:查表1大寒与小雪,大寒夜半漏为“二十六刻 七十六”,小雪夜半漏为“二十六刻 九十六”;而大寒的昏去中星为“八十五度 六”,我们用“同左”表示,小雪的昏去中星也是“八十五度 六”。
因此,实际上,表1中共有两栏数字,其中“夜半漏”,是夜漏刻的一半;“昏去中星”,是昏时刻太阳到中星的距离。

表1 《皇极历》夜半漏与昏去中星原始数据
表1中的夜半漏有4处不同、昏去中星有3处不同,严敦杰根据对称性,对这些数据以及冬至夜半漏的数据给出了8条校勘。陈美东根据严敦杰的校勘结果,通过夜半漏来归算昏去中星,对后者又给出了8处新的校勘。这些校勘,采取的根据有二,其一,24气的对称性;其二,昏去中星是根据夜半漏归算出来的。
严敦杰和陈美东的假设是有道理的,不过,他们都忽略了一个事实,那就是,《皇极历》24气的夜半漏常数,不仅满足对称性,而且可能构成了一个高阶的差分表。另外,在根据夜半漏归算昏去中星常数时,陈美东没有考虑各气昏去中星常数之转分(余分)的取舍值的累积效果,由此导致了昏去中星计算结果与原文多处不合,需要校改的现象[4]。
为了搞清楚表1的构造方法,我们首先需要明确夜半漏与昏去中星的数学关系。假设某日昏时刻太阳的宿度为A、中星的宿度为B,令s表示恒星年的长度,则有
由于夜刻=100-昼刻=2×夜半漏,推得:昼刻=100-2×夜半漏。因此有:

所以,昏去中星,就是昏时刻太阳与中星的宿度差。按《皇极历》恒星年

《皇极历》的昏去中星和夜半漏有如下的关系
昏去中星=(50-夜半漏)×3.662576(度)
(1)
因此,昏去中星的数据,可以根据夜半漏归算出来。为此,需要考察《皇极历》24气夜半漏刻的构造方法。
通常,我们可以根据二分二至,将一个回归年划分为四个部分,对于漏刻表来说,冬至和夏至前后,分别是对称的。因此,漏刻表,基本上可以按照冬至前后、夏至前后的6气数据,分别讨论他们的构造方法。
2 冬至前后漏刻表的校正
中国传统数理天文学中的很多天文数表,都可以从差分表的角度来进行分析。例如,我们曾经复原的《大衍历》晷影差分表,就是一个分段的高阶差分表[5]。由于差分表的构造,具有明确的数学意义,因此,一组数据如果构成了一个完整的高阶差分表,就不是可以随意凑出来的。我们可以利用高阶差分表的这个性质,复原或校正历法中的出现了部分错乱数据的天文表。
对于《皇极历》的漏刻表,我们首先以冬至为中心,讨论秋分到春分各气夜半漏常数的构成。根据表1的原始数据,如果进行一点点微调,我们发现,其中的冬至前后的夜半漏,构成了一个完美的5阶差分表,如表2所示。其中“原文”一栏的数据录自表1中的“夜半漏”,单位为“分”,若相应各气的夜半漏原文数据与表2第三栏的“夜半漏”数据相同,则不予录写。例如,立冬的夜半漏原文数据为25.985刻,与表2中的第三栏“夜半漏”数据相同,故未录写。

表2 《皇极历》夜半漏的差分表(冬至前后)
冬至夜半漏原文为27.42刻,应为27.43刻,这个数据已经为严敦杰校改。实际上,根据表1中的夏至昏去中星118度40分,可以验证《皇极历》的夏至夜半漏为17.57刻,与记载相符,由此可以很容易推出,冬至夜半漏为45-17.57=27.43刻。
根据对称性,立春与立冬的夜半漏应该相等,显而易见,立春的25.865刻,出现了错误,应与立冬的25.985刻一致。大寒与小雪的情形类似,两者的夜半漏也应该相等,严敦杰校改为26.76刻,接近正确。
显而易见,《皇极历》冬至前后各气的夜半漏常数,构成了一个非常完整的5阶差分表。现在的问题是,原文记录小寒与大雪夜半漏均为27.26刻,大寒夜半漏为26.76刻,它们与差分表的相应数据均只差0.005刻,是否需要校改?
为此,我们可以通过对冬至前后各气昏去中星常数的归算,来进行验证。
根据表2校改后的夜半漏数据,按照公式(1),可以归算冬至前后相应各气的昏去中星常数,如表3所示。第四栏“昏去中星”的1度=52转分,其中的“转分”,是将第三栏数据的小数部分乘以52得来的。例如:冬至日昏去中星的计算
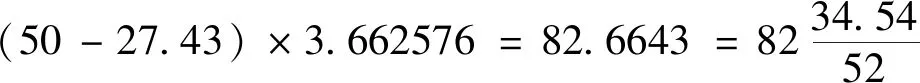
第五栏的“累积分”是从冬至起,累加各气第四栏的“转分”,再减去各气第六栏的“取整”数据得到的,这个结果相当于,本气第四栏的“转分”,加上前一行的“累积分”,再减去其“取整”值,例如:立春与立冬的“累积分”
49.75+5.62-6=49.37
第六栏的“取整”值是根据第五栏的数据的“累积分”,按四舍五入得到的。
根据表3,原文记录的昏去中星,除了冬至日的“82度 转分47”明显有误之外,只有小寒与大雪的转分15与原文的转分16稍有差异,其余结果,完全吻合。

表3 《皇极历》昏去中星数据的推算(冬至前后)
那么,如果我们对小寒与大雪、大寒与小雪等四气的两个夜半漏数据不进行校改,结果会是怎样的呢?表4显示,小寒与大雪的夜半漏取27.26刻时,归算的昏去中星为83度14分,与原文(83度16分)不同;而大寒与小雪的夜半漏取26.76刻时,归算的昏去中星为85度7分,亦与原文(85度6分)不同。因此,此四气的昏去中星常数均需要校改,而此时的夜半漏,不再符合表2所展示的完整的差分表。
对于高阶差分表,数据的些微调整,就可能破坏整个差分表的完整性。因此,要构造一个5阶差分表,绝非易事。构造出表2这样的5阶差分表,完全不可能是一种巧合,一定是人为的结果。由此可以判定,大寒与小寒等四气的两个夜半漏数据,应该按照表2第三栏“夜半漏”的数据进行校改。

表4 小寒与大寒夜半漏必须校正的原因
另外,陈美东将冬至的昏去中星值校正为“82度 转分34.5”([3],页47),如此,则无论是否对大寒与小寒等四气的两个夜半漏进行校改,都会影响到立春到春分、秋分到立冬等各气的昏去中星的归算结果。例如,此时,立春与立冬的昏去中星的归算结果,均为87度50分,与原文的87度49分不同,从汉语的叙述来说,“五十”与“四十九”是非常不同的,出现这种讹误的可能性相对较小。
综上所述,从数表构造的规范性、与原文的贴近程度、昏去中星的归算结果等方面考量,《皇极历》冬至前后的夜半漏与昏去中星的数据,都应该根据表3中第二栏的“夜半漏”与第七栏的“计算结果”进行校正。
3 夏至前后漏刻表的校正
根据前面的论述,我们可以确认,《皇极历》冬至前后的夜半漏常数,是按照表2所示的差分表构造出来的。按照漏刻的对称性,夏至前后各气的夜半漏常数,应该符合相同的构造规律。由此,我们不难根据原始数据,推算出一个结果,如表5所示。
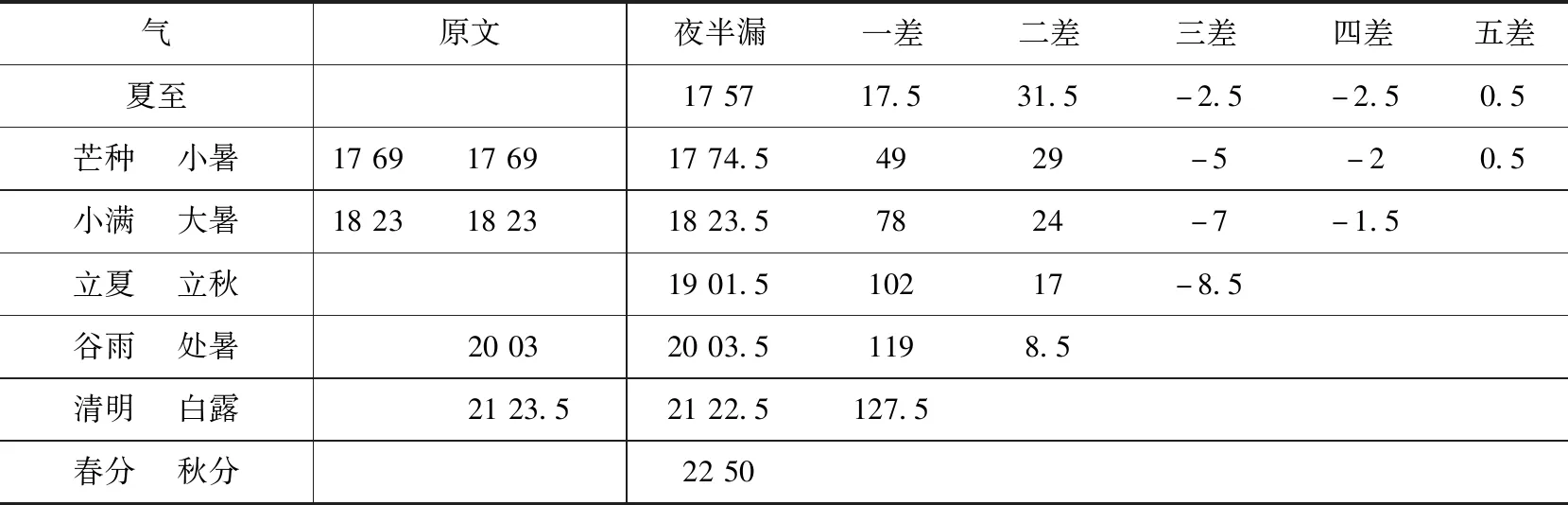
表5 夜半漏的差分表(夏至前后)
与表2类似,表5中第二栏“原文”的数据,录自表1,单位为“分”。这一栏对应各气的数据若与第三栏的“夜半漏”数据相同,则付之阙如。
按照表5,除了处暑与白露两处明显的错误之外,原文中芒种与小暑的17.69刻、小满与大暑的18.23刻,都与差分表的数据不同。这两组数据,究竟有没有问题,我们仍然通过对昏去中星的归算来进行验算。
根据表5中符合差分表的夜半漏,按照公式(1),可以归算夏至前后相应各气的昏去中星常数,结果如表6所示。其中各栏目的计算方法和意义,见上一节对表3的解释。在表6中,昏去中星的计算结果,芒种与小暑为118度8分,转分8与原文的转分18不同;小满与大暑为116度17分,转分17与原文的转分19也是不同的。
那么,芒种等四气的两个数据的差异,究竟是原文的讹误,还是有别的原因呢?

表6 根据5阶差分的夜半漏刻推算夏至前后两气的昏去中星
我们按照《皇极历》夜半漏的原始数据,重新归算夏至前后的昏去中星,结果如表7所示。发现只有清明与白露的转分“21”与归算结果的转分“20”稍有误差,其余计算结果与原文完全吻合。这就说明,《皇极历》夏至前后的夜半漏常数,应该是没有完全采纳表5构造的那个5阶差分表,而是对其中的两个数据进行了调整,其中小满与大暑的夜半漏18.23刻,应该是从18.235刻约化而来;芒种与小暑的17.69刻,与差分表的17.745刻差别较大,应该是根据一些其他因素调整的结果。其余各气的夜半漏常数,照录表5中的5阶差分表。

表7 《皇极历》昏去中星数据的推算(夏至前后)
通过这些计算,可以确定,《皇极历》夏至前后的夜半漏常数,应该是先按照冬至前后夜半漏的5阶差分表(表2)的构造方法,构造了夏至前后各气的夜半漏常数,如表5所示,然后,通过将小满与大暑的夜半漏调整为18.23刻,将芒种与小暑的夜半漏调整为17.69刻,而得到《皇极历》夏至前后各气夜半漏的历取值。再根据这些夜半漏的历取值,归算出《皇极历》夏至前后各气的昏去中星的历取值,如表7所示。
表3与表7,分别给出了《皇极历》在冬至前后与夏至前后24气的夜半漏常数,以及据此归算的《皇极历》24气昏去中星度的历取值。从这些计算可以发现,《隋书·律历志》记载的《皇极历》原文,除了冬至日昏去中星度的“转分 47”明显有误之外,只有小寒与大雪的转分“16”与归算结果的转分“15”,以及清明与白露的转分“21”与归算结果的转分“20”稍有误差,其余数据则完全吻合。由此可以确证,表3与表7中记录的24气夜半漏常数与其推算的昏去中星的“计算结果”,应该就是《皇极历》的历取值。
至此,综合表3与表7的结果,可以得到我们对《皇极历》24气的夜半漏与昏去中星常数的校正,我们将这个新的校正结果按照原文的书写形式,罗列如表8所示。

表8 《皇极历》夜半漏与昏去中星表校正结果

续表8
4 结 论
本文发现了《皇极历》24气夜半漏刻常数表的构造形式。刘焯在确定冬至前后各气夜半漏刻的历取常数时,构造了一个完整的5阶差分表,如表2所示。然后,根据对称性,可以构造出夏至前后各气的夜半漏刻常数,如表5所示。不过,由于24气的昏去中星常数,是由相应的夜半漏刻常数归算出来的,根据表7的计算可以证明,刘焯并没有完全照搬表5的夜半漏刻常数,而是在表5的那个夜半漏刻5阶差分表的基础上,对芒种与小暑、小满与大暑的两个夜半漏刻常数进行了调整,其余则采用了表5的差分表的计算结果。我们由此从算法的原理上,对《皇极历》的这个相关的天文数表进行了彻底的校勘。
如表8所示,对原文的48个数据,我们共进行了16处校勘。其中冬至、立春、处暑、白露的夜半漏,雨水、秋分、立冬的昏去中星等7个数据,支持了严敦杰根据24气的对称性所进行的校正结果。小寒与大雪的昏去中星等2个数据,支持了陈美东的校正结果。冬至、清明、白露的昏去中星,与小寒、大雪、大寒、小雪的夜半漏等7个数据,是根据夜半漏刻的5阶差分表而新作的校勘。
本文的发现表明,刘焯在《皇极历》中,有意识地构造了一个5阶差分表,它应该是迄今为止我们所见到数学史上最早的5阶差分表。在13世纪朱世杰创立高阶等差级数的求和公式之前,构造一个高阶差分表,并不是一件容易的事。由此,从算法史的角度来看,这是一项非常了不起的工作。刘焯是如何做到这一点的,我们尚不得而知。但是,隋唐以降,中国数理天文学中涌现了大量的高阶差分表,这些差分表的应用,极大地提升了历法的计算精度[6],刘焯的《皇极历》不仅创立了二阶插值算法,而且创立了高阶差分表,这些工作的影响无疑是深远且重要的,值得我们进一步深入的研究[7]。

