基于贝叶斯网络雷达伺服系统故障树分析

(中国电子科技集团公司第三十八研究所， 安徽合肥 230088)

0 引言

雷达伺服系统是雷达的重要组成部分,它对于发现目标、跟踪目标以及精确地测量目标的位置都起着重要作用。本文研究的雷达伺服系统主要用来控制雷达天线的转动,以完成对飞行目标的稳定跟踪。

针对雷达伺服可靠性的研究，国内和国外的可查文献很少，说明对这方面的研究我们还处在一个相对空白的位置，这就为我们研究雷达的伺服可靠性提出了迫切要求；然而现在雷达伺服系统多年来存在着许多可靠性方面的问题。例如海上盐雾对天线座内有刷电机碳刷的腐蚀、系统天线转数无法提高、插销机构锁定失控、平台功放电路的烧管和跟踪失控等一系列问题。深入开展某型雷达伺服系统的可靠性分析与研究，既是预防和解决型号生产使用中技术风险的基本技术手段，又能降低装备全寿命周期费用，提高装备整体效能，也可对当前的雷达伺服系统可靠性分析给出一个指导性的可靠性分析方法，填补在该项领域里的可靠性分析空白，对以后类似雷达产品的伺服系统可靠性设计给出了指导性思想，提高相关产品的可靠性。

本文采用基于贝叶斯网络的故障树法，对雷达伺服系统进行建模分析。将故障树转化为贝叶斯网络，快速准确地求解出了顶事件“随动失败”的发生概率。另外计算出了各底事件的概率重要度，找出了导致顶事件发生的关键影响因素，对提高雷达伺服系统可靠性具有一定的指导意义。

1 雷达伺服系统

本文所研究的雷达伺服系统，在该型雷达上主要作用是接收来自接收机提供的方位、俯仰角误差信号，完成对目标的被动跟踪以及在显控分系统角度信息引导下，完成对目标程序跟踪。本套伺服系统包括两套伺服分系统，以下简称主伺服分系统和从伺服分系统。从伺服分系统受显控系统工作模式控制，跟随主伺服分系统随动或不动，两个伺服分系统通过通信形成有效连接。

主伺服分系统的任务是通过控制主天线座方位轴和俯仰轴的运动使天线指向目标，同时将主天线座角度信息传送给从伺服分系统，从伺服分系统根据收到的主天线角度信息驱动从伺服分系统的天线座，并将目标的定位数据传送给中心控制设备。绘制本伺服系统功能流程图如图1所示。

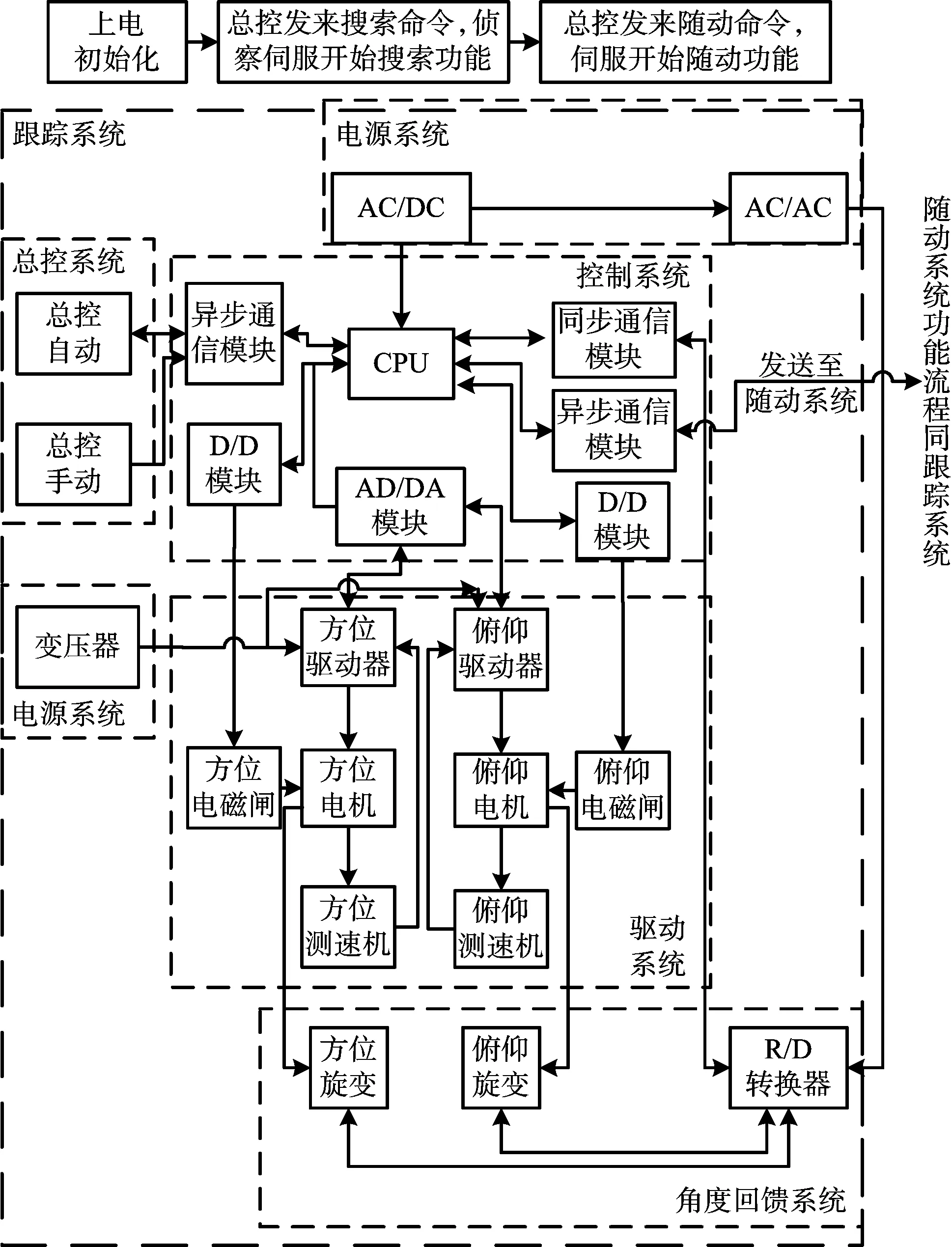
图1 伺服系统功能流程图

功能流程图的每一个方框代表一个硬件单元，以每一个硬件单元(部件)作为一个模块来分析，对于模块内部的器件不再进行分解，箭头表示了数据的流向，在假定的这个功能模式下，所有的模块都是全寿命，即从命令开始，所有的部件都是需要正常工作系统才能完成任务。故障模式就是从伺服转台无法完成转动功能，这个故障的起因就是因为在这种故障模式下，所有的部件都需要参与工作，并且该伺服系统中的主伺服分系统和从伺服分系统都在这种模式下参与任务执行，而且对外部的接口也都需要参与任务，在这个模式下可以分析所有部件可靠性。

该流程图中，总控发送命令到异步通信口，发送从伺服转台随动命令，并且发送方位和俯仰需要到达的角度，从伺服控制器收到命令后，首先松开方位轴和俯仰轴的电磁闸，再根据送来的命令进行运算，求解出方位和俯仰轴对应的角度，通过同步通信口读取R/D转换器，R/D转换器读取方位角度旋转变压器和俯仰角度旋转变压器的角度信号，得到当前方位轴和俯仰轴角度，通过控制器CPU计算得到转动的方向和速度，然后通过AD/DA模块发送对应的转速和方向信号给电机驱动器，电机驱动器发送大电流信号驱动电机转动，电机转动后带动测速机转动，并且将测到的速度反馈给驱动器进行闭环控制，在这个过程中，通过异步通信口发送跟踪系统的当前方位角度和俯仰角度给从伺服系统，从伺服系统的余下工作模式同主伺服系统。

在本文研究中，假设软件是可靠的，在这里不再讨论该伺服系统的软件实现。

2 建模分析

故障树分析法(FTA)是一种对复杂系统的可靠性、安全性进行分析的有效工具，它把所研究系统的最不希望发生的故障状态作为故障分析的目标，然后寻找导致这一故障发生的所有直接原因，接着再细化，深入分解、跟踪每一种可能的原因，直到最基本、不可再分的原因确定为止[1]。利用故障树可以分析系统发生故障的各种途径，计算各个可靠性特征量，对系统的安全性和可靠性进行评价，进而根据FTA的结果，确定系统关键部位、薄弱环节、应对措施等。但故障树分析需要花费大量的人力、物力及时间来进行建模和定性定量分析。

贝叶斯网络是一种概率图形模型，通过有向无环图来表达变量之间的依赖和独立关系，即节点在给定其父节点的前提下与其后代节点条件独立，并且利用条件概率分布刻画了变量对其父节点的依赖关系[2]。每个节点都附有一个概率分布，根节点X所附的是它的边缘分布P(X)，或称先验分布，而非根节点Xi所附的是条件概率分布P[Xi|Pa(Xi)][3-4]。

具体地，如果贝叶斯网络模型揭示的条件独立关系成立，则网络中变量的联合概率为

P(X3|X1,X2)P(X1)P(X2)

(1)

式中：U={X1,…,XN}为变量；Pa(Xi)为变量Xi的父集；P[Xi|Pa(Xi)]为变量Xi的条件概率。

例如，当观测到关于变量X3的新信息时，可据此更新得到变量X1和X2的后验概率：

P(X1,X2|X3)=

(2)

复杂系统对故障树进行最小割集求解时，可能出现基本事件较多，最小割集相交等情况，使得顶事件发生概率的计算十分复杂。而贝叶斯网络中每个节点X只会受到与其相关联的节点的影响，因此能够通过边缘化求解机制推理出所有与概率相关的问题。变量间独立关系的存在减少了确定变量联合概率分布所需的参数，从而简化了系统中变量的概率模型。所以，本文基于贝叶斯网络对雷达伺服系统进行故障树建模分析。

2.1 故障树和贝叶斯网络模型建立

从本雷达伺服系统中选取“随动失败”作为顶事件进行故障树分析。根据雷达伺服系统的功能原理及相关数据资料，对随动失败这一事件进行致因分析，得出了该事件故障树的基本事件及系统工作半小时后各部分的失效概率分布，如表1所示。

表1 基本事件及其概率分布

2.1.1 基于故障树的因果建模

对随动失败进行因果关系分析，将导致该事件发生的原因分为3类：从伺服系统故障(M1)、主伺服系统故障(M2)和总控命令没有成功发送。建立故障树如图2、图3、图4所示，其中T表示随动失败。

图2 总故障树

图3 故障树事件

图4 故障树事件

2.1.2 基于贝叶斯网络的可靠性分析模型

通过故障树分析，明确随动失败与基本失效事件的因果关系后，采用映射算法将故障树转化为贝叶斯网络进行顶事件发生概率求解，如图5所示。映射法由Bobbio等[5-7]提出，其映射包括图形映射和数值映射。在图形映射中，故障树的基本事件、中间事件及顶事件与贝叶斯网络中的根节点、中间节点及叶节点一一对应，且节点的连接方式与相应故障树的对应事件的连接方式相同。在数值映射中，基本事件的发生概率被配置为根节点的先验概率，而中间节点和叶节点则由故障树的逻辑门翻译得到条件概率表[8-9]。

图5 随动失败贝叶斯网络示意图

2.2 故障树分析

2.2.1 顶事件发生概率分析

计算得到系统工作0.5 h的伺服系统顶事件的发生率为0.000 149，事件发生的可能性等级处于110-4级，说明该事件的发生处于中等概率。

在故障树中，主伺服系统与从伺服系统包含的基本事件相同，以从伺服系统为例进行分析。造成从伺服系统故障的原因包括角度指向不正确(M3)、无法发出正确控制命令(M6)以及天线不转(M8)，计算得到它们的发生概率分别是0.000 017 26,0.000 011,0.000 043 9。可见天线不转是导致随动失效的主要故障。

2.2.2 重要度分析

基本事件的重要度主要包括结构重要度、概率重要度及关键重要度三个内容。结构重要度分析是从故障树的结构上来分析各基本事件的重要程度。在不考虑各基本事件的发生概率，通过分析排列出各基本事件的结构重要度顺序，从而了解各基本事件对顶事件发生影响的程度，以便按重要度顺序采取防范措施，是一种定性的重要度分析。本伺服系统中，其每个部件构成一个最小割集且不相交，结构重要度都相同，就不再进行具体分析。

概率重要度是指第i个部件不可靠度的变化引起系统不可靠度变化的程度。用数学公式表达为

(3)

式中:Δgi(t)为概率重要度；Fi(t)为元部件不可靠度；g[FS(t)]为顶事件发生的概率；F(t)= [F1(t),F2(t),…,Fn(t)]；FS(t)为系统不可靠度，FS(t)=P(T)=g[F(t)]。

由全概率公式：

P(T)=P[Xi(t)=1]·P[T|Xi(t)=1]+

P[Xi(t)=0]·P[T|Xi(t)=0]=

Fi(t)g[1i,F(t)]+

[1-Fi(t)]g[0i,F(t)]

(4)

将式(4)代入式(3)得

Δgi(t)=g[1i,F(t)]-g[0i,F(t)]=

E[Φ(1i,X(t))-Φ(0i,X(t))]=

P{[Φ(1i,X(t))-Φ(0i,X(t))]=1}

(5)

本伺服系统根据厂家提供底事件发生率可以求出每一个部件的Δgi(t)，t=0.5 h，

Δg1(t)=(1-F2(0.5))·(1-F3(0.5))·…·

(1-F42(0.5))

Δg2(t)=(1-F1(0.5))·(1-F3(0.5))·…·

(1-F42(0.5))

⋮

Δg42(t)=(1-F1(0.5))·(1-F3(0.5))·…·

(1-F41(0.5))

通过概率重要度分析，主伺服R/D转换器和从伺服R/D转换器最重要，4台驱动器为第二重要的器件，AD/DA模块为第三重要的器件，这些器件是在实际工作中需要重点检查检测的器件。结合实际的故障情况，在设备运行过程中，R/D转换器出现故障2次，驱动器出现故障1次，AD/DA模块出现故障2次。

3 结束语

雷达伺服系统是雷达系统的重要组成部分，雷达伺服系统能否可靠地工作是保证雷达系统能否完成任务的重要保障。本文基于贝叶斯网络对雷达伺服系统进行了故障树建模分析，具体的研究工作首先对雷达伺服系统的结构、功能分析，建立功能流程图；再进行雷达伺服系统故障树的分析，根据雷达伺服系统的组成结构及功能流程，对所有可能发生的故障因素进行分析，绘制“随动失败”事件的故障树；将故障树转化为贝叶斯网络，求得该事件发生的概率；对故障树进行重要度分析，找出系统的可靠性薄弱环节。

本次研究意义在于掌握一种可靠性的实际分析方法，并且将该方法运用于实际的工程实践中，在本次研究过程中，通过故障树的定量分析找出系统的需要重点检查检测环节。这次研究过程中发现的该型雷达伺服可靠性问题可以为以后的可靠性设计工作起一定的指导作用，在相似的雷达伺服系统设计中，如何提高这些可靠性的薄弱点，在某些薄弱环节尽量采取并联回路设计或者其他的方法提高雷达伺服系统可靠性提供了帮助。