一种抑制多路OFDM信号峰均比的SG-PTS算法

高 洋，项炳龙，宫丰奎

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)作为多载波调制的一种，具有高频谱效率、抗频率选择性衰落和易实现等优点，已被广泛应用在多个通信标准中，如IEEE802.11a[1]、IEEE802.16(WiMAX)[2]和3GPP LTE[3]等。随着信息时代的飞速发展，越来越多的场景对高速多路数据传输业务提出了需求，如车联网系统、实时监控系统等，多路正交频分复用系统能很好地满足上述场景的需求。IEEE802.11p即为一种采用多路正交频分复用传输技术的标准。众所周知，正交频分复用信号存在峰均比(Peak-to-Average Power Ratio, PAPR)过高的问题，这一问题对多路正交频分复用信号变得更为严重。高峰均比信号经过功放等非线性器件时会产生严重的带内失真与带外辐射。造成系统误比特率性能下降以及临带干扰。

针对降低单路正交频分复用系统的峰均比问题，已提出了多种有效算法。传统的压扩法[4]通过压缩大信号，扩大小信号来抑制信号峰均比，但会造成信号的带内失真以及带外辐射，在多路正交频分复用系统中，带外辐射会导致严重的临带干扰，严重降低系统误码率(Bit Error Rate, BER)性能，因此压扩法难以用于多路正交频分复用信号；星座扩展法[5-7]通过对时域信号进行削峰，再将信号变换到频域后根据扩展后的星座图对信号进行调整，从而降低信号的峰均比。该算法在单路正交频分复用系统且调制阶数不高的场景下，能起到较好的峰均比抑制作用，但同样不适用于多路正交频分复用信号的峰均比抑制，主要原因在于星座扩展法需先对多路正交频分复用信号进行削峰滤波得到单路正交频分复用信号，继而将其变换到频域后对信号进行调整，导致计算复杂度过高，不易于实现；另外一类是部分传输序列法[8-11](Partial Transmit Sequences, PTS)算法，该算法通过对频域信号进行分组并分别乘以一个相位旋转因子，进而选择最优的相位旋转因子组合来降低信号的峰均比。然而，将传统部分传输序列算法应用于多路正交频分复用系统时，多路正交频分复用信号叠加后，当出现某些符号相位相近时，仍然会产生幅值较大的信号，因此不能直接应用于多路正交频分复用信号的峰均比抑制。

综上，笔者借鉴了部分传输序列算法的原理，提出了一种分组部分传输序列(G-PTS)算法。该算法首先对多路正交频分复用信号进行分组并将组内信号相加，继而将相加得到的信号分别乘以一个相位旋转因子后再次相加，通过选择最优相位旋转因子组合降低信号峰均比。此外,在G-PTS算法的基础上，通过降低其寻找最优相位旋转因子的计算复杂度，进一步提出了简化分组部分传输序列(SG-PTS)算法。

1 多路正交频分复用系统

1.1 系统模型

多路正交频分复用系统框图如图1所示。通过生成多个基带正交频分复用信号，并分别调制至不同载波频点，然后在时域上叠加，进而得到多路正交频分复用信号。

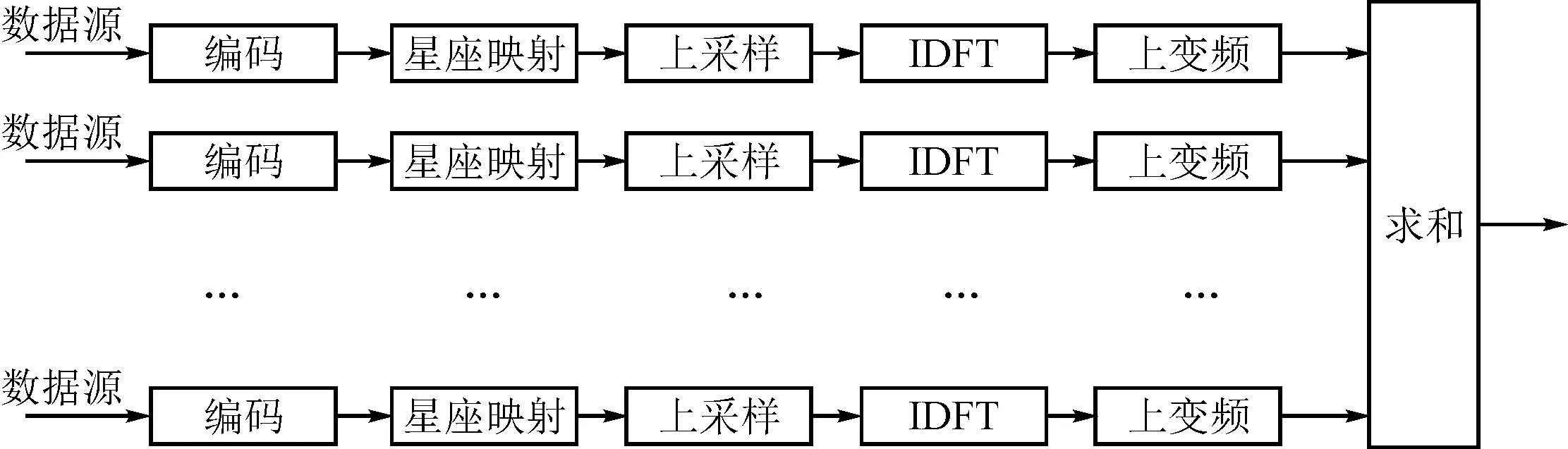
图1 多路正交频分复用系统框图

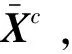
这里，Xc中包含LN-N个0，其中L和N分别表示上采样率和子载波个数。

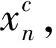
(1)

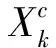
最后，将上变频后的信号在时域直接叠加可得多路正交频分复用信号sn，即

(2)

其中，fc表示第c路信号的载频，Ts表示符号周期。

1.2 峰均比的定义

根据文献[12]中的结论，当上采样因子L≥4时，离散正交频分复用信号的峰均比近似于连续正交频分复用信号的峰均比，所以单路正交频分复用信号的峰均比通常定义为

(3)

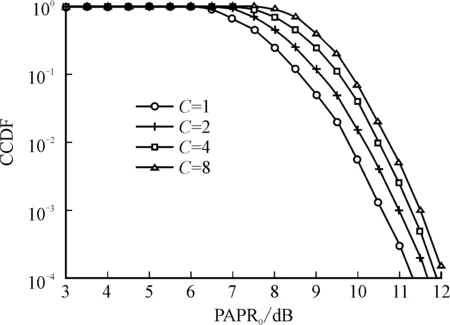
图2 多路正交频分复用信号的峰均比曲线

其中，xn表示时域正交频分复用信号,E表示求数学期望。

因此，由式(2)可得多路正交频分复用信号的峰均比可定义为

(4)

一般用互补累积函数(Complementary Cumulative Distribution Function, CCDF)表示正交频分复用信号的峰均比超过阈值PAPR0的概率[13]。图2显示了多路正交频分复用系统的峰均比曲线，其中子载波个数为64，上采样率为32，调制方式为64QAM。如图2所示，随着信号路数C的增加，正交频分复用系统的峰均比明显增加。

2 传统的单路部分传输序列算法

图3 PTS算法的实现框图

部分传输序列算法的实现原理如图3所示。首先，将频域数据X利用串并转换将其分割为M组子块，分割后的子块满足

(5)

其中，X(m)表示分割后得到的第m子块。根据分割方式的不同，可分为随机分割、交织分割和相邻分割，其中随机分割能得到最好的峰均比抑制效果[14]，故所提算法皆采用随机分割。

对分割后的每一组数据进行离散的傅里叶逆变换,可得

x(m)=TIDFT(X(m)),m=0,1,…,M-1 。

(6)

然后，通过相位旋转序列b={bm=exp(jθm),m=1,2,…，M},θm∈{j2πv/V,v=0,1,…,V-1}，将各个子块组合，得到

(7)

通过选择最优的相位旋转序列可使信号的峰均比达到最优。部分传输序列算法的峰均比抑制性能随着分割子块数的增加而改善，但其最优旋转相位序列的搜索复杂度随分割子块数呈指数增长[15]。

3 提出的降峰均比算法

3.1 分组PTS算法

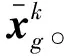
(8)

利用相位旋转序列p={pg=exp(jθg),g=1,2,…,G},θg∈{j2πv/V,v=0,1,…,V-1}，将各个分组信号组合，得到

(9)

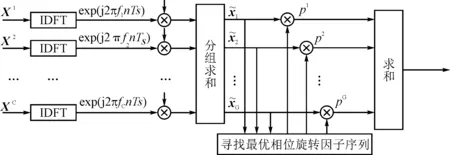
图4 G-PTS算法的实现框图

当改变相位旋转序列p时，s(p)的峰均比也随之改变。通过遍历所有可能的p，寻找最优的p使s(p)的峰均比达到最小。

下面针对式(9)进行计算复杂度分析。在式(9)中，相位旋转序列p一共有VG种可能性，所以计算所有的s(p)需要LNVG次复数乘法和(G-1)LNVG次复数加法。

3.2 简化分组部分传输序列算法

为了降低寻找最优相位旋转序列的计算复杂度，在G-PTS算法的基础上，进一步提出了简化分组部分传输序列(SG-PTS)算法。以8路正交频分复用系统为例，为了实现的简单，可将旋转相位因子集合定义为

p={pg=exp(jθg),g=1,2,…,8} ,

(10)

其中，θg∈{j2πv/V,v=0,1},即相位旋转因子取值为1或-1。

如果不进行重新分组，则相位旋转序列p有256(28)种可能性。根据前一节的分析结果，提出的G-PTS算法针对式(9)的计算复杂度为1 792LN次复数加法。

为了降低G-PTS算法的实现复杂度，进一步提出了一种简化的G-PTS算法，即SG-PTS算法。利用p0～p255表示p的256种情况，其中p0={1,1,1,1,1,1,1,1},p1={-1,1,1,1,1,1,1,1},…,p255={-1,-1,-1,-1,-1,-1,-1,-1} 。对应处理后的信号可以表示为s(p0)～s(p255)。在已知s(p0)时，可通过下式求得s(p1):

(11)

通过式(9)求得s(p1)，需要7LN次复数加法。现利用式(11)，只需要LN次复数加法。同理，利用s(p0)和s(p1)可以得到s(p2)和s(p3)：

(12)

(13)

以此类推，可以通过上述算法得到s(p1)～s(p255)。除了计算s(p0)时需要7LN次复数加法，计算s(p1)～s(p255)中任意一个则只需要LN次复数加法。用类似二叉树的结构来表示这种计算形式，如图5(a)所示。

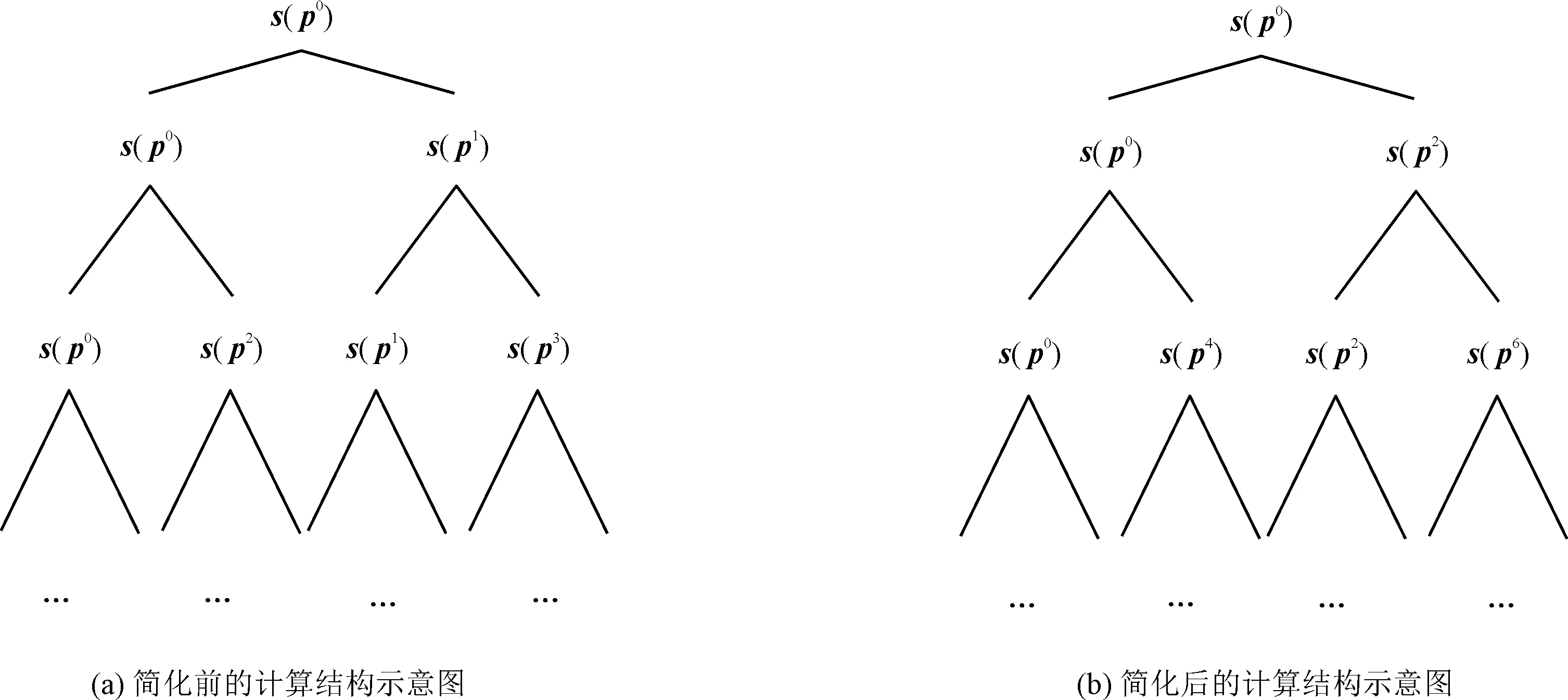
图5 SG-PTS算法简化前后的计算结构示意图

当pk=-pn时，s(pk)=-s(pn)，此时s(pk)和s(pn)的峰均比是一样的。在遍历p时，应避免出现pk=-pn的情况。故重新规定p={p1=1,pg=exp(jθg),g=2,3,…,8}，从而保证∀pk,pn∈p满足pm≠-pn。故图5(a)的计算结构示意图可以修正为图5(b)所示。

表1 不同算法的计算复杂度比较

针对提出的两种算法，表1比较了G-PTS算法和SG-PTS算法的计算复杂度，SG-PTS算法计算s(p)只需7LN+(27-1)LN=134LN次复数加法，而G-PTS算法计算s(p)则需要1 792LN次复数加法。与G-PTS算法相比，SG-PTS算法在不影响峰均比抑制性能的同时，显著地降低了计算复杂度。

4 仿真结果

利用计算机仿真，对前面提出的G-PTS算法和SG-PTS算法进行了分析和比较。仿真中采用的系统参数如下：多路正交频分复用系统的支路数为C=8，子载波个数为N=64，调制方式为64QAM调制，上采样倍数L=32。另外，为了保证接收端能正确检测发送端的信号，这里假设接收端已知发射端采用的最佳相位旋转序列。

图6显示了G-PTS算法的峰均比性能与分组数G和旋转相位因子集合中因子数V的关系曲线。从图6可以看出，随着分组数G和因子数V的增大，峰均比的抑制效果越好，增大分组数G带来的峰均比抑制效果越好于增大因子数V带来的效果。

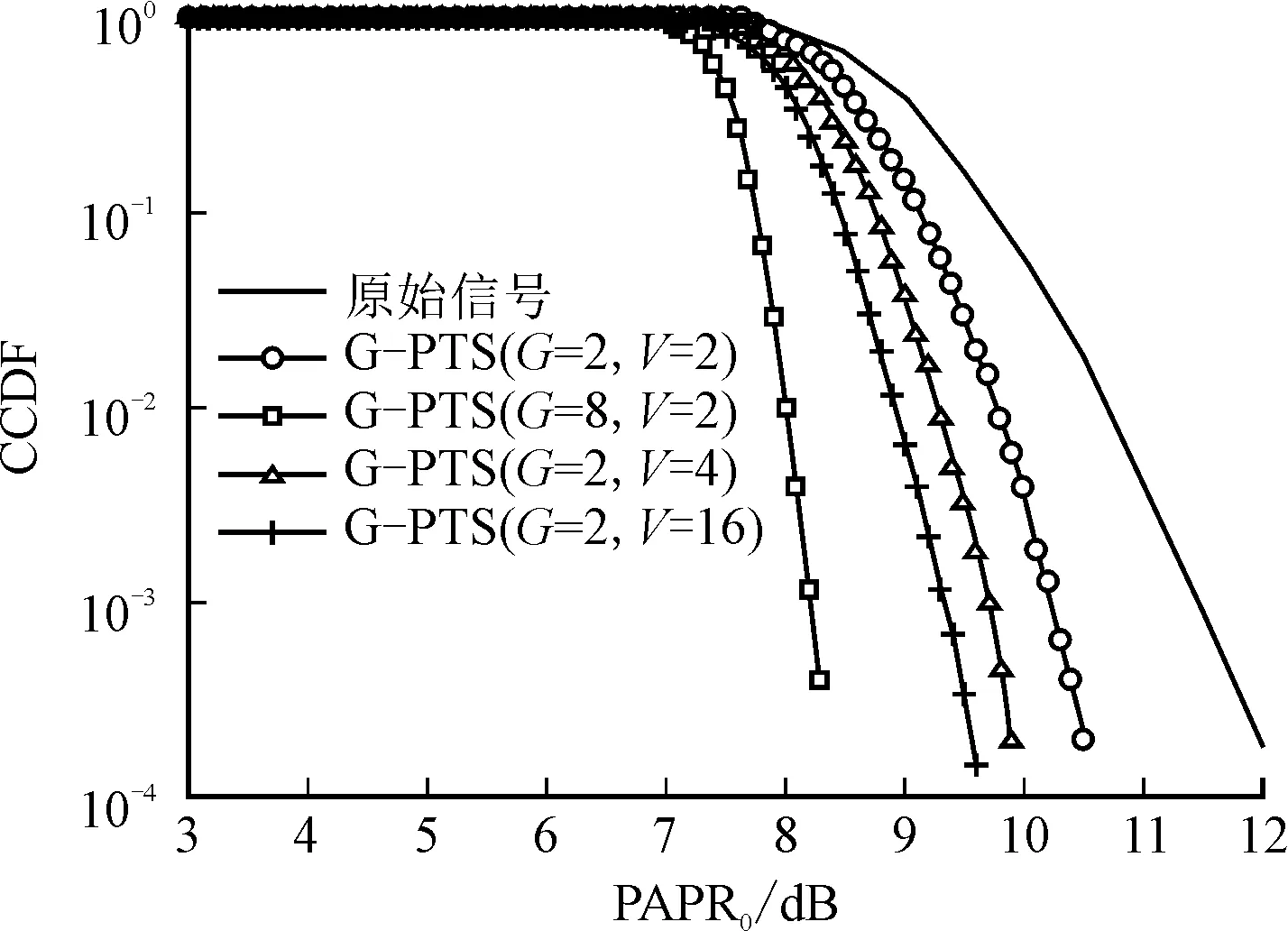
图6 G-PTS算法的峰均比性能与G、V的关系曲线

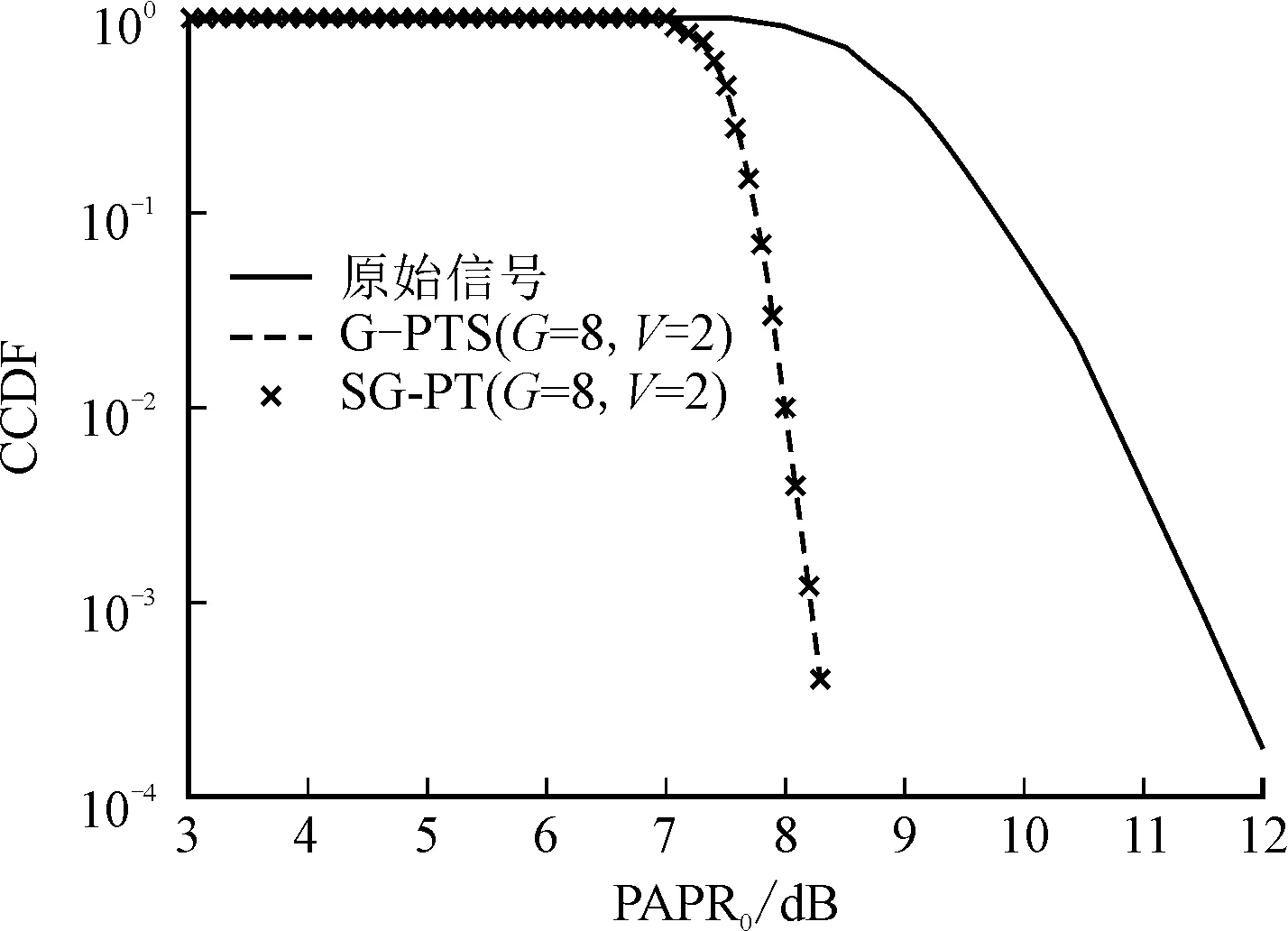
图7 SG-PTS算法和G-PTS算法的峰均比性能曲线

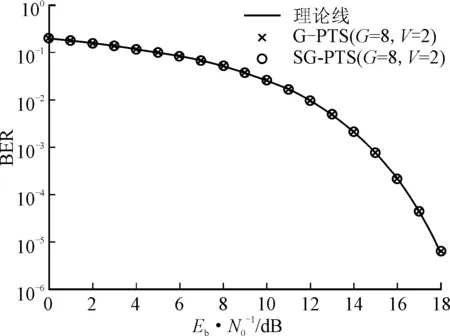
图8 SG-PTS算法和G-PTS算法的误比特率性能曲线

图7和图8分别比较了SG-PTS算法和G-PTS算法的峰均比性能和误比特率(Bit Error Rate,BER)性能。从图7可以看出，SG-PTS算法和G-PTS算法的峰均比性能完全一致。从图8可以看出，在接收端已知发射端采用的最佳相位旋转序列时，G-PTS算法和SG-PTS算法的误比特率仿真曲线与理论曲线是完全吻合的。这说明SG-PTS算法可以在保证多路正交频分复用系统传输性能的同时，可以有效降低算法的实现复杂度。另外，由于仿真没有考虑非线性器件(比如功率放大器)对系统误比特率性能的影响，因此，提出的两种将峰均比算法的误比特率与传统单载波系统的误比特率性能完全一致，具体的误比特率理论公式可以参见文献[16]。

5 结束语

传统的部分传输序列算法能够有效抑制单路正交频分复用系统的峰均比，但是无法直接应用于多路正交频分复用系统。基于传统PTS的实现原理，提出了G-PTS算法和SG-PTS算法，同时对上述两种算法的峰均比抑制性能和实现复杂度进行了分析比较。仿真结果表明，提出的SG-PTS算法能有效抑制多路正交频分复用系统的峰均比,且实现复杂度适中。