能量协作下中继系统性能推导及仿真分析
刘向丽,刘冬妮,李海娇,李 赞
(西安电子科技大学 通信工程学院,陕西 西安 710071)
目前,在无线通信网络中,中继既能协助信源节点传输数据到达目的节点,又能在节省发射功率的同时提高系统容量[1-2],因此中继技术成为通信领域的研究热点之一。但由于中继节点的频繁使用和无法实现节点电池的定期更换,导致网络中出现能量空洞问题,进而影响传感器网络的寿命,而能量收集技术的出现恰好可以克服这一瓶颈[3]。
最初,能量收集技术考虑从周围环境中收集能量,依靠阳光、风和潮汐等来支持通信设备。1958年,太阳能直接转换为电能成为一项突破性的成就,在此启发下,各种形式的能量与电能之间的转化被广泛研究,但应用范围仅限于近场。而射频(Radio Frequency,RF)信号的发展为远场能量传输打开了新格局[4]。HU等[3]整理分析了近些年的能量收集以及能量传输关键技术,详细阐述了从周围环境中收集能量具有不可预测、低效率等特点,并对从射频信号中提取能量的硬件技术进行了评估,提出射频信号能够实现无线能量传输[5-7],同时这些能量逐渐倾向于随时随地充电[8]。此外,无线射频信号可以同时携带能量和信息[9-11]。由于能量收集技术能够有效的延长传感器网络的寿命,近年来越来越多的研究将能量收集与中继技术结合在一起。2011年,GUNDUZ和DEVILLERS[12]研究了三节点通信模型,假设源节点能量受限,中继节点能量采集供电,同时分析不同中继工作模式对系统吞吐量的影响,提出了最优的功率分配方案。文献[13]中的能量中继模型是将中继节点的电池状态建模为马尔可夫模型,并配备有存储功能的双态电池,且通过无线能量传输使得中继节点电池被充电,在译码转发协议下,提出了基于单向两跳中继信道对应于不同状态信道瞬时信息要求和实现复杂性的中继选择策略,并得到了系统的中断概率。而文献[14]中以最小丢包率为优化准则,提出新的中继节点能量模式,即源节点与中继节点都能够从周围环境中收集能量,且中继节点在向目的节点发送数据的同时向源节点传输能量。在通常情况下,因为中继节点无法准确地获知源节点的位置,所以在一定程度上忽略了能量传输方向的可行性以及传输过程中能量的损耗。
考虑以上的研究工作,笔者提出的能量中继模型是瑞利衰落下的单中继单天线模型。其中源节点与中继节点都可以从周围环境中收集能量,并且源节点可以向中继节点进行无线能量传输,传输的能量一部分被中继节点用于解码,另一部分存储在中继节点中。此外,通信过程依据电池的能量状态选择直通链路或者中继链路,结合电池稳态分布条件,推导出随机中继选择(Random Relay Selection, RRS)方案的中断概率表达式,并以传输数据消耗能量的最小化为目标,中断概率门限为约束条件,利用粒子群算法进行优化问题求解。
1 系统模型
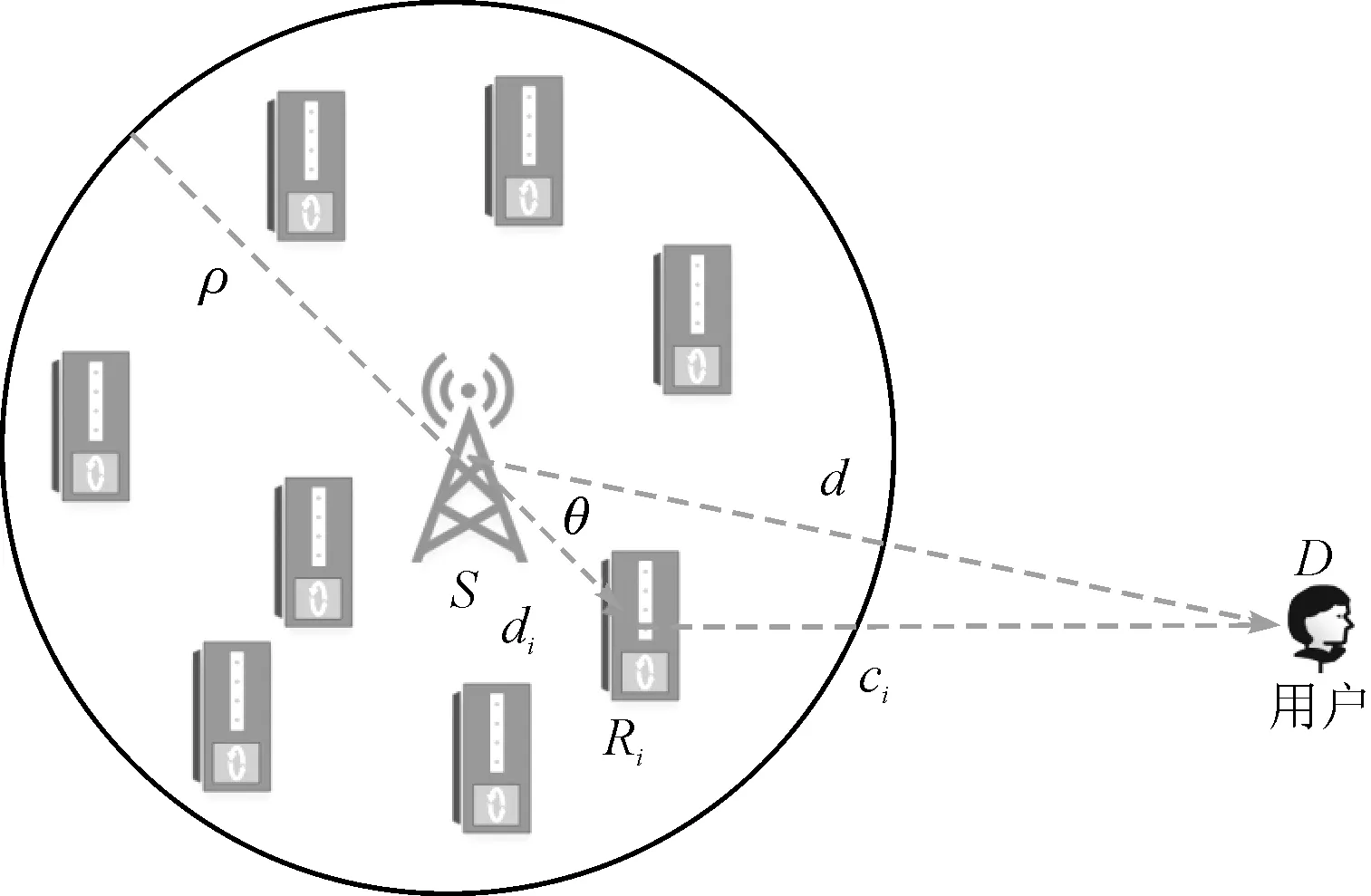
图1 三节点的中继传输网络模型
一个三节点的中继网络如图1所示。网络由一个源节点、一个目的节点和多个采用解码转发方式的中继节点组成,分别标记为S,D和Ri,i∈{1,2,…,n}。假设S和D之间存在直接链路,且源节点位于圆形网络的几何中心,引入一个半径为ρ的圆形网络,将S到D的距离标记为d,S到R的距离标记为di,R到D的距离标记为ci。
与传统技术不同,假设源节点和中继节点配备的电池容量为无限大,能够从周围环境中收集能量并进行存储。在第n个时隙,源节点和中继节点收集到的能量分别表示为ES[n]和Er[n],其中E[·]为统计平均值。在初始阶段,源节点依据自身能量状态选择通信链路。当源节点储能状态大于其向目的节点发送数据消耗的能量时,选择直通链路进行通信。源节点相邻时隙的能量关系表示为[14]
LS[n+1]=LS[n]+ES[n]-δSD,
(1)
其中,LS[n]是第n个时隙源节点电池的储能状态,LS[n+1]是第n+1个时隙源节点电池的储能状态,ES[n]是源节点从环境中收集到的能量,δSD是源节点向目的节点发送数据所消耗的能量。因此可得到源节点的电池稳态分布[14]:
(2)
若中继协作,则源节点每发送一个数据包消耗的能量为δSR,其中βδSR的能量被存储于中继节点,(1-β)δSR的能量被中继解码消耗,0≤β≤1。因此可知,中继节点的能量来源为从环境中收集到的能量与源节点发送的能量之和,且二者相互独立。相邻时隙源节点与中继节点的电池稳态能量分别为
LS[n+1]=LS[n]+ES[n]-δSR,
(3)
LR[n+1]=LR[n]+ER[n]+βδSR-δRD。
(4)
式(4)中,LR[n]是第n个时隙中继节点电池的储能状态,LR[n+1]是第n+1时隙中继节点电池的储能状态,ER[n]是第n个时隙中继节点从环境中收集到的能量。源节点与中继节点带电的概率为
(5)
(6)
考虑到中继节点无线设备的限制,中继节点难以同时发送和接收消息,所以采用半双工模式,在电池瞬时状态和中继节点位置信息未知的情况下,以随机的方式选择中继节点,即随机中继选择方案。此方案一般分为两个时隙传输:第一个时隙源节点随机选择第i个中继节点来进行数据的传输;如果第i个中继节点完全有电且处于未通信状态,在第二个时隙将对来自于源信号的信息进行解码并转发到目的节点,否则中继处于收集模式。又由于无线信道遭受小范围的块衰落和大规模的路径衰落,所以中继节点和目的节点接收到的信号可表示为以下两式:
(7)
(8)
其中,XS是源节点发送的数据,XR是中继解码后转发的数据,PSR和PRD分别为源节点和中继节点的发射功率,hSR是源节点到中继节点通信链路的信道系数,hRD是中继节点到目的节点通信链路的信道系数,α是路径损耗因子,nSR和nRD分别表示中继节点和目的节点处的均值为0、方差为1的加性高斯白噪声。相应的中继链路的信噪比分别为
(9)
(10)
类似地,若源节点选择直通链路,即S→D链路,则接收到的信号与信噪比分别为
(11)
(12)
其中,PSD是直通链路下源节点的发射功率,nSD表示目的节点处的均值为0、方差为1的加性高斯白噪声。假设信道衰落是服从瑞利分布的,信道功率增益为|hi|2,在平均信噪比为1的条件下,其概率密度函数和累积分布函数分别为
f|hi|2(x)=exp(-x) ,
(13)
F|hi|2(x)=1-exp(-x) 。
(14)
所以,直通链路的信道功率增益的累积分布函数可以表示为
(15)
2 瑞利衰落下的中断概率分析
一个通信系统性能是由相应的指标来进行衡量的。对于无线中继网络来说,中断概率成为衡量其性能的主要指标。
当链路容量不满足所要求的用户速率时,中断事件就会发生,所以通信链路能否发生中断也取决于链路的平均信噪比及其信道衰落分布模型。由定义,中断概率可表示为
Pout=P{c (16) 其中,r0代表信息的传输速率,ε为信噪比门限。由香农定理可知,ε=22r0-1。 根据以上介绍,源节点可以利用两条通信链路完成信息的传输。当不满足直通链路条件时,选择中继链路。所以对两条链路分别进行讨论。 (1)直接链路正常通路,考虑同时满足以下两个条件。 (a)若源节点能量大于门限值,则 PS=PR{LS[n]≥δSD} 。 (17) (b)若信道容量大于阈值,则由式(15)知, (18) 由式(17)和式(18),可得直通链路正常通路的概率为 (19) (2)中继链路通路,需要同时满足以下3个条件: (a)若源节点的能量值不满足直传条件而满足中继传输的条件,则同时中继节点的电池状态符合传输状态为 PR=(1-PS)×PR{LS[n]≥δSR}×PR{LR[n]≥δRD} 。 (20) (b)利用几何泊松点过程,在半径为ρ的圆上生成n个中继节点。在通信过程中,被选择参与通信的中继节点称为候选中继节点。当候选中继节点集合不为空集时,概率P{N≥1}表示为 P{N≥1}=1-exp(-λπρ2) , (21) 其中,λ代表中继节点的密度,ρ为中继网络模型的半径,N是候选中继节点的总个数,n是网络中中继节点的总个数,N≤n。 (c)若源节点到中继节点链路和中继节点到目的节点链路的信噪比同时大于中断门限,则源节点到中继节点的链路信噪比大于中断门限表示为 (22) (23) 因为两信道之间相互独立,最后可表示为 (24) 由以上内容,可知中继链路通路的概率为 (25) 分析以上提出的中继选择方法可知,只有当直通链路和中继链路同时中断时,系统通信才中断。所以,中断概率可以表示为 (26) 结合以上分析,可知瞬时时刻消耗的总能量为 E=PR{LS[n]≥δSD}×δSD+(1-PR{LS[n]≥δSD})×PR{LS[n]≥δSR}× (δSR+PR{LR[n]≥δRD}×δRD)。 (27) 因此,在中断概率受限的条件下,找出源节点和潜在中继节点的能量分配,以使传输数据的能量最小。该问题由如下数学模型描述: (28) 式(28)中包含能量的约束性。当中继协作时,源节点和中继节点发送数据消耗的能量小于直接传输时源节点发送数据消耗的能量。η为中断概率门限值,可依据具体通信环境设定,且0≤η≤1。由优化问题分析,粒子群算法因其全局和局部搜索能力强,收敛速度快,随机选取参数的特性,在通信链路性能分析时有较好的效果,进而选择粒子群算法求解优化问题。 粒子群算法起源于观察鸟群觅食的行为,基本观念是模拟鸟类的群体行为所建构的群体智能模式,通过鸟群中个体之间的协调和信息共享来寻找最优解。在算法中,用粒子来替代鸟,在速度与位置的共同作用下,粒子通过计算适应度函数值调整位置,直到获得全局最优解[15]。具体步骤如下: (1)初始化一组随机粒子,由优化问题知粒子在三维空间进行搜索,则第j个粒子的位置以表示为Xj=(xj1,xj2,xj3),速度表示为Vj=(vj1,vj2,vj3),其中xj1,xj2和xj3分别代表着自变量δSD,δSR和δRD,所以粒子的位置范围0 (2)依据优化问题目标函数式(27),计算粒子的适应值,再更新粒子个体极值pbesty和全局极值gbest。由上文知,每次迭代得到的全局最优解一定是最优解中适应值最小的解。 (3)由式(29)和式(30)来更新粒子的速度与位置,在式(27)中参数c1和c3是[0,1]内的两个随机值,c0表示控制粒子在搜索空间中的惯性权重,c2和c4是非负常数,当达到迭代终止次数,则算法终止,输出最优解,否则返回步骤2,继续搜索。 Vj=c0×Vj+c1×c2×(pbestj-xjn)+c3×c4×(gbestj-xjn),n=1,2,3 (29) Xj=Xj+Vj。 (30) 图2 粒子群算法的能量曲线 由粒子群算法仿真得到图2,图中所示的曲线为寻找最优解的过程,可以看出在迭代次数为400次时,在最小能量为1.165时停止了位置的更新,在中断概率门限为0.2时,得到最小能量,其对应的最优解为δSD=2.07,δSR=0.26,δRD=0.66。 为了验证数据与能量传输模型公式的准确性,对其进行了仿真,给出了能量协作下的随机中继选择方案和文献[13-14]的中断概率性能对比曲线,如图3所示。可以看出,随着源节点发射功率的增大,文中方案的中断概率收敛速度更快,始终保持最小,最终小于10-1,说明笔者提出方案的性能更好。图3的仿真参数设定如下:σ2=1,r0=0.01,λ=2,ρ=1,d=8,β=0.8,,ES[n]=ER[n]=0.5。 图3 性能对比曲线 图4 最小能量曲线 图4描绘了中断概率与最小能量的关系。图4中d=2,从曲线的整体趋势可以看出,中断概率随着消耗能量值的减少而增大。中断概率越接近于1,系统传输数据消耗的最小能量值越小。当中断概率小于0.1时,曲线较为平滑,此时选择中继传输的概率增大。由式(2)知,选择直传的概率由22.8%降到10.6%。中继协作的概率由77.2%增加到89.4%,而中继链路消耗的能量值趋于稳定。可知选择中继链路可减少通信过程中消耗的能量。笔者在中继链路中引入能量协作的思想,因此能量协作可减少通信过程中的能量消耗,具体能量变化如表1所示。 表1 中断概率小于0.1的传输方式一览表 以传统的三节点中继通信模型为基础,针对传感器网络能量受限问题,笔者提出一种新的能量传输模型。假设源节点与中继节点都具有能量采集功能,且源节点向中继节点同时发送能量和数据,基于随机中继选择方案,引入了源节点依据概率选择直通链路或中继链路的思想,推导出中断概率表达式,并以中断概率为限制条件,将传输过程能量消耗作为优化函数,利用经典粒子群优化算法进行求解,得到能量消耗最小值以及此时的参数分配情况。仿真结果表明,笔者提出的模型能够获得较低的中断概率,证明了能量协作可明显地减少通信过程中消耗的能量。
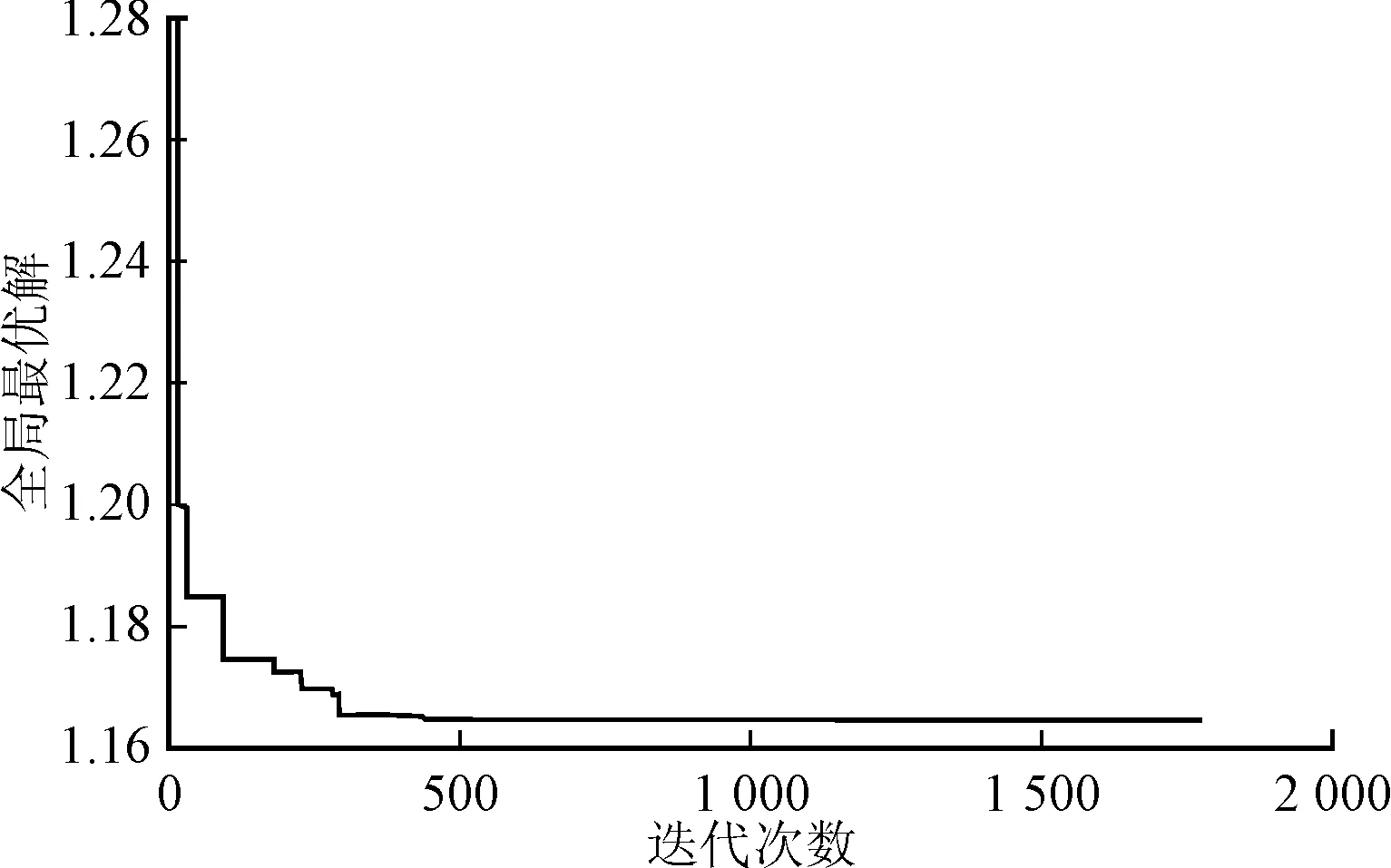
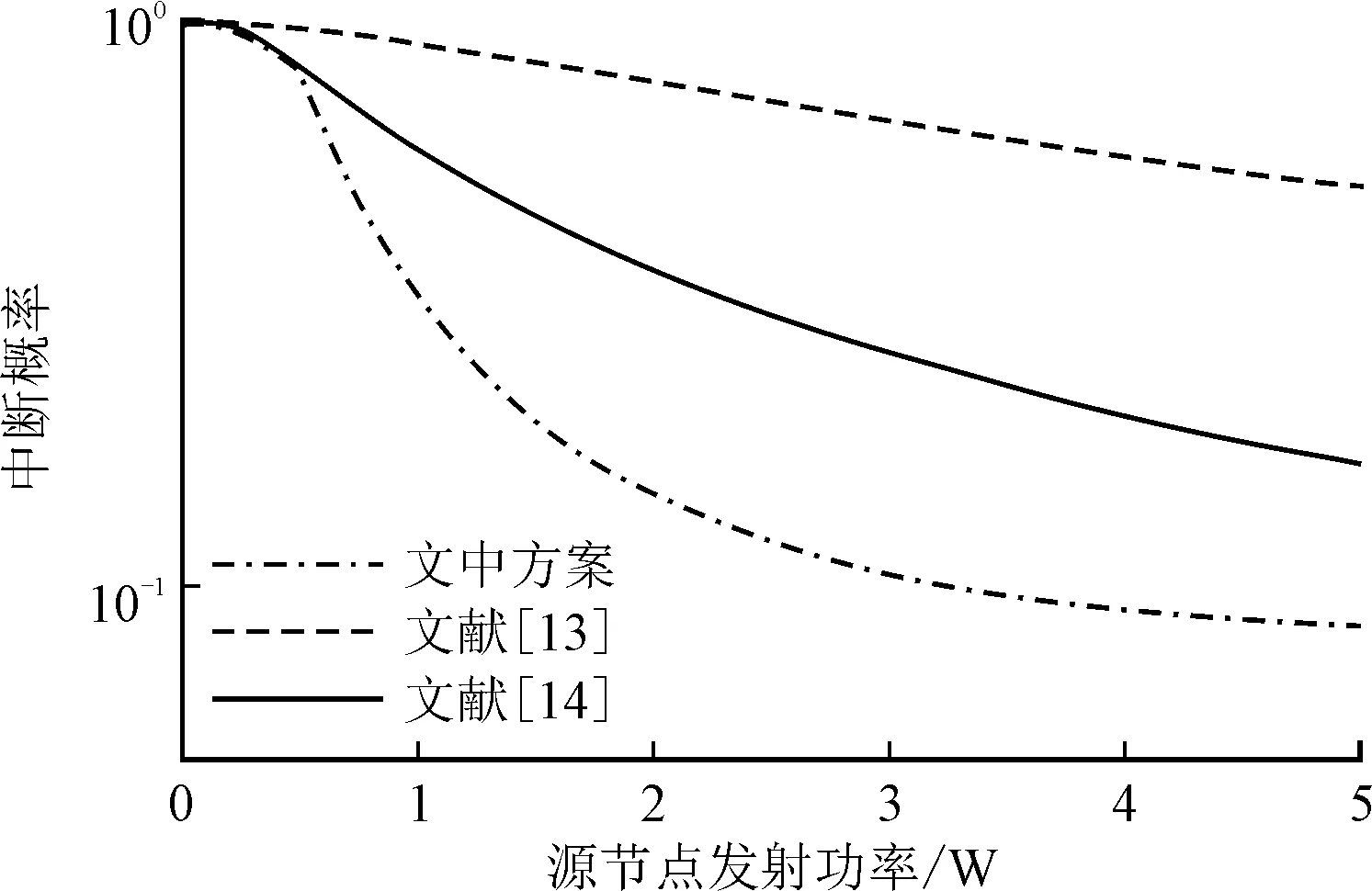
3 仿真结果与分析


4 结束语

