时频域分解海面回波及慢速微弱目标检测

左 磊，产秀秀，禄晓飞，李 明

(1.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安，710071；2.中国酒泉卫星发射中心 甘肃 酒泉，735000)

海面后向散射电磁波产生海杂波，其特性与海面粗糙程度以及发射信号的极化、带宽和波长等因素有关，表现为强的非平稳性[1-3]。远距离探测时，入射角很小，发射信号与海面波浪产生类似于镜面反射效应，海杂波能量急剧增大，频谱扩展严重[4]。

由于海杂波的复杂性及慢速微弱目标的多普勒频率非常靠近海杂波，传统的基于动目标检测的方法效果不佳。分形特征能够较好地描述海面回波的形状特征，可以用来检测海面慢速微弱目标，但需要很长时间积累，不具有实时性[5]。文献[6-7]应用海杂波白化抑制和正随机过程建模后，再利用特征检测实现海面飘浮小目标检测。将海面慢速微弱目标在一定时间内建模成微动模型，利用时频分析等微多普勒分析工具进行海面慢速微弱目标检测的方法吸引了大量学者的注意[8-10]。时频分析可以显示目标的瞬时运动特性，是检测海面慢速微弱目标的有力工具，其中时频分解方法在抑制海杂波及目标检测中表现出明显的优势。文献[11]利用平稳小波变换进行海面回波信号分解后，再利用固有熵特征进行目标检测。文献[12]提出了利用极化特征分解的方法进行海面目标检测的方法。文献[13]基于逆维格纳威尔分布(Wigner-Ville Distribution, WVD)提出了基于S方法(S-Method, SM)的信号分解方法，并应用该方法检测海面目标。S方法的信号分解方法在将海杂波分解成多个信号分量的同时，容易将两目标信号分裂成若干部分，出现漏警或虚警。

根据遮隔维格纳威尔分布(Masked WVD, MWVD)和逆维格纳威尔分布,笔者提出了基于时频迭代分解的海面慢速微弱目标检测方法。对比S方法的信号分解方法，迭代分解方法在分解海面回波时，通常将海杂波分解成一个或两个信号分量。并且目标信号分量不会分裂，因而虚警率较低。迭代分解方法对于在时频域非常接近且能量相差较大的两调频信号分量具有较强的分辨能力，可以从海面回波中分解出海面慢速运动目标的回波信号。

1 海面慢速微弱目标检测方法

基于信号的逆维格纳威尔分布和遮隔维格纳威尔分布，笔者提出了一种基于时频迭代分解的海面目标检测方法。该方法能够将海杂波分解成一个或两个信号分量，因此能够较快地分解出目标信号分量。下面首先简要回顾一下逆维格纳威尔分布变换，再提出两个目标信号与海杂波之间的判别准则，最后提出目标检测方法。

1.1 逆维格纳威尔分布变换

信号f(n)的维格纳威尔分布变换的离散形式可以表示为

(1)

此处省略了常数因子2，其中，Wf(n,k)表示信号f(n)在离散时间为n、离散频率为k时的维格纳威尔分布，N为信号长度，f*(n)是f(n)的共轭。信号的维格纳威尔分布可以看作对二维函数f(n+m)f*(n-m)进行一维离散傅里叶变换。其逆离散傅里叶变换可表示为

(2)

其中，n1=n+m，n2=n-m。式(2)的矩阵形式可以表示为

R=f(n)f*(n) ，

(3)

其中，f(n)为信号f(n)的列向量形式，自相关矩阵R通过对式(2)的插值得到。对方阵R进行特征分解可以发现，仅有一个非0特征向值λ1=Ef(Ef为信号能量)。根据λ1及其对应的特征向量u1(n)构造信号：

(4)

1.2 目标信号与海杂波之间的判别特征

如果从海面回波信号中利用逆维格纳威尔分布提取出一个信号，如何判定该信号是目标信号还是海杂波是一个非常棘手的工作，笔者拟利用下面两个特征进行目标信号判别。

准则1信号维格纳威尔分布的能量聚集。文献[13]指出，在时频域目标信号的能量比海杂波集中。因此，文中将信号分量维格纳威尔分布的最大值的平方与其和之比作为目标信号判定准则。由于式(4)中u1(n)的能量为1，且其维格纳威尔分布与原信号的维格纳威尔分布只相差一个能量因子，所以能量聚集性Crit的表达式可简化为

(5)

根据准则1进行如下判断：

(6)

其中，P0是目标检测门限。

准则2用来区分目标信号和海尖峰，可通过下式进行判断：

(7)

其中，T0是目标检测门限，Trit是信号分量的持续时间。

1.3 海面慢速微弱目标检测方法

假设海面回波信号中包含海杂波、目标信号和其他干扰等，则可以用一个长度为N的多分量信号表示为

(8)

其中，i表示多分量信号f(n)的第i个分量(i=1,2,…，M)。且当信号分量序号iEfj。

多分量信号的维格纳威尔分布包含各分量的自项和分量之间的交叉项。遮隔维格纳威尔分布是一种保留信号维格纳威尔分布中各分量自项并抑制交叉项的方法[14]，基于逆维格纳威尔分布和定义的两个准则，文中提出基于时频迭代分解的海面慢速微弱目标检测方法。

步骤1计算信号f(n)的遮隔维格纳威尔分布。计算海面回波信号f(n)的2N点短时傅里叶变换(STFT)，经频谱折叠得到位于归一化频率-0.25～0.25范围内的数据，记为C(n,k)。使用硬门限对其进行时频域滤波，得

(9)

m=aE(|C(n,k)|) ，

(10)

其中，E(|C(n,k)|)为|C(n,k)|的整体均值，a为修正系数。将CM(n,k)与海面回波信号的维格纳威尔分布相乘得到遮隔维格纳威尔分布。

步骤3根据准则1和准则2判断分解出来的分量是不是目标信号，如果是，说明已经检测到目标，则不再进行下面步骤的操作；否则,继续下面步骤。

步骤4从信号f(n)中滤除f1(n)。构造信号fc为

(11)

该过程将f1(n)分量补偿到归一化频率零处。构造阻带为归一化频率0.002，阻带衰减为-60dB，凹口位于归一化频率0处的31阶陷波器h(n)，对fc(n)滤波并进行频率校正，得到信号fr(n)的表达式如下：

(12)

其中，⊗表示卷积。

步骤5令f(n)=fr(n)，并将其中的分量按能量从大到小的顺序命名为f1(n),f2(n)…。重复步骤1到5。

由于海杂波的频域扩展性，基于S方法信号分解的目标检测方法会将海杂波分解成多个大能量的分量，同时会将海面目标信号分解成多个分量，降低了信号的能量。而文中方法，将海杂波和目标回波分别分解成一个或两个信号分量，较大地提升了算法的效率。所以在文中方法中，可认为如果3次迭代后没有检测到目标，则认为该回波信号中只有海杂波，没有目标信号。

2 实验结果与分析

文中所有的极化方式为垂直极化(VV)海杂波数据(19 931 107_135 603_starea.cdf)是在浪高2.1 m时由X波段雷达在低入射角情况下收集的[15]。雷达工作在烧穿模式，脉冲重复频率为1 000 Hz(对应归一化频率为1)，带宽为5 MHz。该数据包含14个相邻的距离单元和131 072次回波。目标信号位于第9距离单元，影响第8～11距离单元。

2.1 仿真目标的检测与分析

图1(a)为第1个距离单元内海杂波的频谱，可以看出海杂波的能量主要集中在归一化频率-0.08～0.02之间。通过长为512(0.512s)的滑动汉明窗从第1个距离单元内取数，每一次取出的数据之间有50%的重合，将窗内数据进行快速傅里叶变换后依据最大值归一化，得到归一化谱图，部分结果显示在图1(b)中。可以看出，X波段海杂波的瞬时频率中心和带宽是不均匀的[2]，海杂波的主体位于0 Hz～-50 Hz之间(归一化频率为0～-0.05)，同时在0 Hz～50 Hz之间(归一化频率为0～0.05)也有能量扩展。

图1 第1个距离单元内的回波数据

图2 文中方法和基于S方法的信号检测结果

仿真产生慢速微弱目标信号S1(n)=b1exp(-π((n-250)/400)2)exp(-j2π(0.000 05n2+0.05n))其中，0≤n≤511，b1为信号幅度。将S1(n)加入海杂波(第5距离单元的第63 489-64 000点，其杂噪比为19.5 dB)中构造一个信杂比为-10 dB的海面回波信号，利用文中方法和基于S方法的检测结果如图2所示。从图2(b)和(c)可以看出，通过文中方法检测出的目标信号与实际信号是一致的，而图2(d)显示了经S方法分解后信号S1(n)的特征向量的时频聚集性，检测结果为构造信号中不含目标，是一个漏警。

图3 检测概率

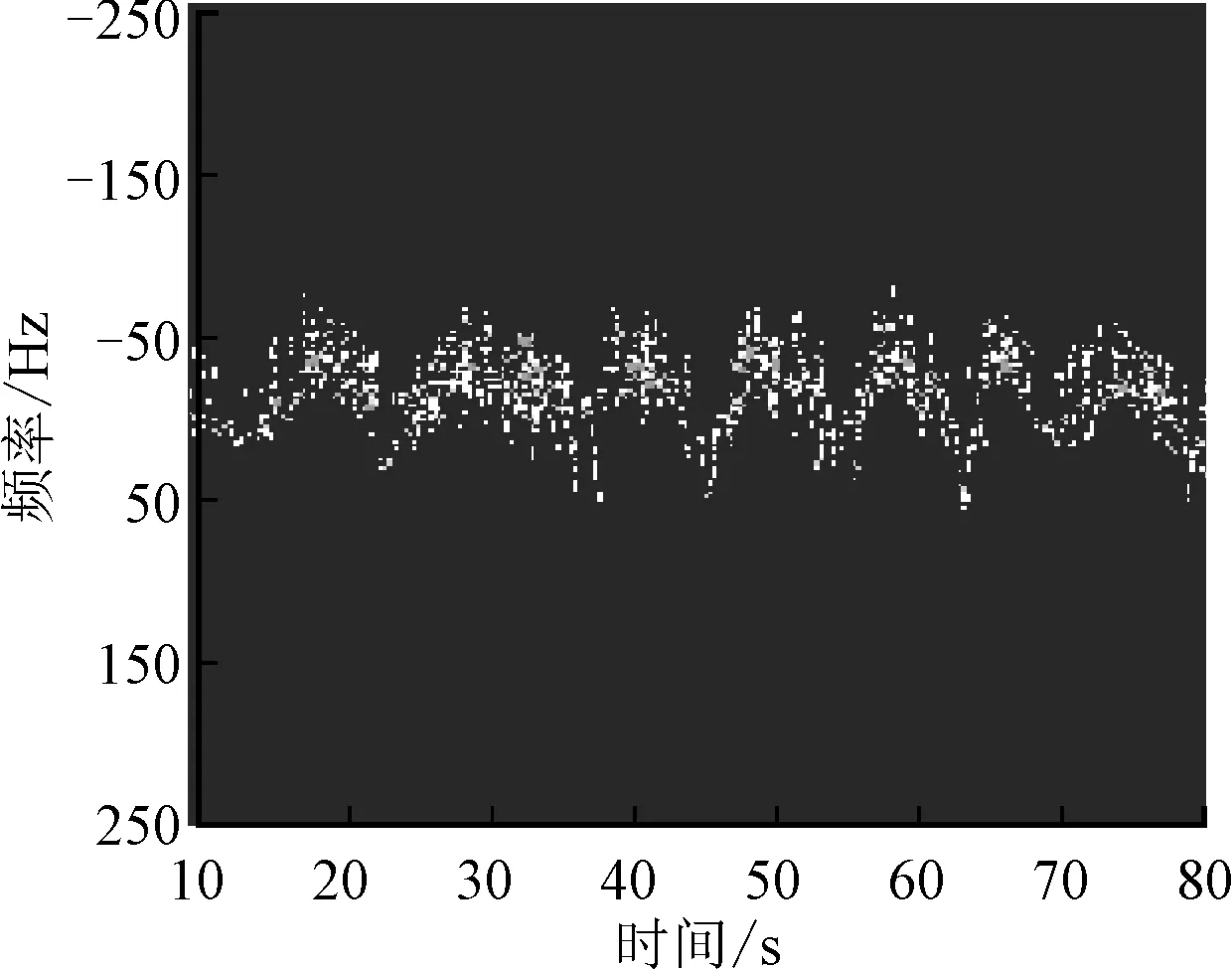
图4 第9个距离单元内回波数据的归一化谱图

2.2 实际目标的检测与分析

已知第9个距离单元内有一个微弱目标，该目标在与其相邻的距离单元内仍然可见[15]。该距离单元的归一化谱图显示在图4中。从中可以看出，当长波长海浪经过该距离单元时，海杂波的带宽和频率中心较大，目标淹没在海杂波中；当没有长波长海浪经过时，目标较为明显。因此文中从第9个距离单元中取两组典型的长为512的回波数据，其起始点分别为60 s(长波长海浪经过该距离单元)和 64 s(该距离单元内没有长波长海浪)。

图5 60 s处数据的目标检测结果

图6 64 s处数据的目标检测结果

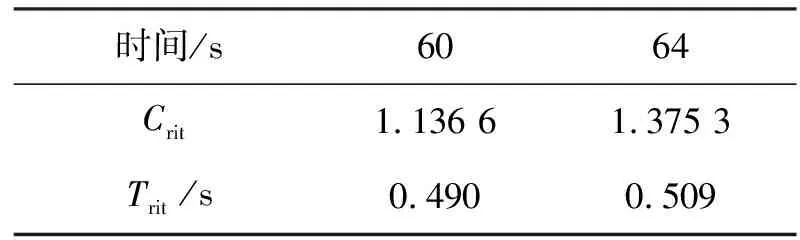
表1 检测结果

两组数据的频谱分别显示在图5(a)和图6(a)中，由于目标信号在频域的位置与海杂波重合，因此无法在频域检测出目标。两组数据的维格纳威尔分布分别显示在图5(b)和图6(b)中，从中可以较明显地观测到目标信号。应用文中方法对这两组数据进行目标检测，其判别过程(P0=1，T0=0.3s)如表1所示。检测出的目标信号的维格纳威尔分布分别显示在图5(c)和图6(c)中。从中可以看出，海面固定目标在不同的时刻具有不同的运动状态，相应地，其多普勒频率也不同。在第1组数据中，目标处于匀加速运动状态，这是由长波长海浪经过引起的。在第2组数据中，目标近似匀速运动，速度接近于-0.15m/s。

目标在第8个距离单元内依然可见，但能量较小，因而具有较低的信杂比。从第8个距离单元内抽取出第13.5s处的数据，其频谱和维格纳威尔分布分别显示在图7(a)和7(b)中，从中都无法判断该数据中是否含有目标。应用文中方法检测海面目标。其中一分解出的信号分量满足Crit=1.120 9，Trit=0.448 s，据此判定该段数据中含有目标。图7(c)为检测出的目标信号的维格纳威尔分布，从中可以看出目标在该时段处于匀速运动状态且运动速度较小。

图7 第8个距离单元目标检测

3 结束语

笔者提出了一种基于时频迭代分解的海面慢速微弱目标检测方法。相对于基于S方法的信号分解方法，笔者提出的方法分解X波段的海面回波时将海杂波作为一个或两个信号分量分解出来，并且不会将目标信号分裂成多个部分，从而降低了海面目标检测的虚警。同时该方法对于在时频域部分重合的信号具有较强的分辨能力，适合在低信杂比情况下检测海面慢速运动目标，同时该方法用样适用于检测海面高速目标。对包含仿真目标与实际目标的海面回波数据的检测结果表明，笔者提出的方法能以较高的精度从海面回波中检测出慢速微弱目标，并且能够得到目标的运动特性。