基于MRAS-RLS算法永磁同步电机参数辨识

刘世交，白国振，胡冬，冯春花，李帅

(上海理工大学，上海 200082)

近年来，永磁同步电机(PMSM)在军事和民用场合应用的范围越来越广，性能要求也越来越高。在很多精确控制和快速定位的场合，伺服系统要求更高的跟踪精度和更好的稳定性。先进的控制策略要求电机参数准确，所以实时地掌握精确的电机参数对设计和分析控制系统稳定性都非常重要。

目前，国内外常用的电机参数辨识方法有： 递推最小二乘法(RLS)、模型参考自适应法(MRAS)、扩展卡尔曼滤波算法和人工智能算法等。RLS可以很好地解决数量和精度的矛盾，但是在辨识的过程中对旧的数据有依赖性，易产生数据饱和现象[1]，所以算法跟随性差。也有学者通过限定记忆和加入遗忘因子的方法用于消除旧数据的影响，提高辨识算法的跟随性[2]，但是辨识精度和跟随性难以同时达到较好结果。MRAS的关键在于设计的自适应规则是否合理，建立准确的可变模型可以确保快速收敛到准确的估计值。扩展卡尔曼滤波算法适用于对实时性要求较高的参数辨识，但辨识过程中需要进行矩阵运算，高阶运算计算量很大，对硬件的要求很高，而噪声估计的合理性、真实的工况模型误差以及计算机有限字长都会导致误差方阵失去正定性，导致算法不能收敛到最优值[3-4]。一些智能算法，如神经网络、遗传算法、蚁群算法等逐渐被应用到参数辨识中，这些智能算法在结构合理、参数选取正确的情况下，可以获得较好的辨识结果，但是由于算法的复杂性、结构的合理性以及参数选取的正确性都对参数辨识产生很大影响，而且算法运算量很大，对硬件要求很高，常用的控制器往往达不到理想的效果[5-6]。

因此，本文提出了一种改进的递推最小二乘法(MRAS-RLS)，用于解决PMSM的参数辨识问题。该算法结合MRAS算法和RLS算法的优点，参数辨识的精度和速度都得到很大的提高，对时变参数的辨识跟随性也很好。通过仿真分析，证明了MRAS-RLS算法比改进前的RLS算法的辨识效果有很大的改进。

1 永磁同步电机数学模型的建立

PMSM定转子之间的位置是变化的，所以电磁关系比较复杂。为了方便建立PMSM模型，使模型合理简化，先做如下假设[7]： 不考虑电机的铁芯饱和情况；不考虑电机中的涡流以及磁滞损耗的情况；不考虑磁场中的空间谐波，三相的绕组对称并且砸数、电阻和轴线位移的角度相同。经过坐标变换，PMSM在旋转坐标系d-q下的数学模型：

1)电压方程如式(1)所示：

(1)

式中：ud，uq——定子电压在d轴和q轴上的分量；id，iq——分别为定子电流在d轴和q轴上的分量；R——定子的电阻；ψd，ψq——定子磁链在d轴和q轴的分量；we——转子的角速度；Ld，Lq——d轴和q轴的电感分量。

2)定子磁链方程如式(2)所示：

(2)

将式(2)代入式(1)中，得到定子电压方程为

(3)

式中：ψf——永磁体磁链，Wb。

3)三相PMSM的数学模型已实现完全解耦，由此得出电磁转矩方程如式(4)所示：

(4)

式中：pn——电机的极对数。

2 MRAS-RLS算法参数辨识算法

2.1 模型参考自适应算法辨识原理

MRAS算法辨识步骤： 先根据工作需求选取参考模型，再选取含有需要辨识参数的可调模型，将两者模型的输出误差值进行比较，按照建立的自适应规则调整模型中的参数值，当参数收敛到某数值时，即为所需要的辨识参数。MRAS算法结构如图1所示。

图1 MRAS算法结构示意

MRAS设计的关键在于自适应律的设计是否合理，本文使用Popov超稳定性理论来确定在线辨识电机参数的自适应律。Popov超稳定性理论是根据时变系统特性提出的，由1个非线性部分组成的反馈通道，前向通道由线性定常部分组成。标准非线性反馈系统结构如图2所示。

图2 标准非线性反馈系统示意

当系统输入为0时，u=-w，前向通道可表示为

(5)

式中：A，B，C，D——状态空间矩阵，且A和B能控，A和C能观。根据Popov超稳定性理论，该系统想要保持稳定状态，必须满足式(6)[8]：

(6)

保持系统稳定的前提条件是G(s)=D+C(SI-A)-1B为严格正实矩阵。Popov超稳定性理论设计的前提，是连续反馈系统在运行中需十分稳定，使得构造的可调模型无限接近参考模型，输出误差趋近于0[9]，进而得出需要辨识出的参数。

2.2 递推最小二乘法辨识原理

Ym=XmΘ

(7)

(8)

进行第m+1次测量，系统方程为

y(m+1)=θ1x1(m+1)+

θ2x2(m+1)+…+θnxn(m+1)

(9)

写成矩阵形式为

Ym+1=Xm+1Θ

(10)

(11)

通过1个矩阵运算恒等式对式(11)进行变换，首先建立该恒等式，如果A，A+BC，E+CA-1B，A+BC均为非奇异方阵，其中E为单位矩阵，则式(12)所示的矩阵恒等式成立：

(A+BC)-1=A-1-A-1B(E+CA-1B)-1CA-1

(12)

P(m+1)=

[P(m)-1+X(m+1)XT(m+1)]-1=

P(m)-P(m)X(m+1)[E+

XT(m+1)P(m)X(m+1)]-1

XT(m+1)P(m)

(13)

将式(8)和P(m)的定义公式相结合，如式(14)所示：

P(m)X(m+1)[E+XT(m+1)

(14)

(15)

2.3 MRAS-RLS算法辨识原理

通过上述分析可知，RLS算法的辨识速度很快，但辨识的误差比较高；而MRAS算法辨识精度很高，但在辨识前期的辨识速度和稳定性却不高。MRAS-RLS算法将MRAS算法引入RLS算法中，利用MRAS参数辨识的优势改进RLS算法的不足，MRAS-RLS算法参数辨识算法结构如图3所示。

图3 MRAS-RLS算法参数辨识结构示意

由图3可知，MRAS算法不仅为RLS模块提供较准确的初值，还将用于辨识PMSM的定子电阻、定子电感、转子磁链、转动惯量。具体的辨识过程如下：

1)使用MRAS算法辨识定子电感、定子电阻、转子磁链、转动惯量4个参数。

3 仿真结果分析

3.1 MRAS-RLS算法仿真模型建立

在Matlab/Simulink模块上，建立矢量控制和脉宽调制的PMSM控制方法，用以PMSM的参数辨识。根据MRAS-RLS算法原理，整合了RLS算法模块和MRAS算法模块的优点，搭建了MRAS-RLS算法辨识模型。

3.2 定常参数辨识仿真结果分析

本文采用大郡公司TS004 PMSM建立仿真模块，电机的基本参数见表1所列。

电机参数按照表1设定，转速设定为900 r/min，基于MRAS-RLS和RLS算法的PMSM参数辨识结果见表2所列。

表1 TS004 PMSM参数

表2 MRAS-RLS算法和RLS算法参数辨识结果对比

根据MRAS-RLS算法和RLS算法辨识结果分析可知，MRAS-RLS算法对定子电感、转子磁链、转动惯量的辨识精度得到了明显的提高，辨识时间也明显缩短，动态过程得到了很大的改善。

3.3 时变参数辨识仿真结果分析

电机运行过程中受到外界各种条件的影响，电机参数经常发生变化，辨识算法需要比较好的跟随性才能更好地对时变参数进行辨识，所以对时变参数的辨识也是MRAS-RLS算法研究的一部分。对PMSM模型的库文件进行解锁、修改和更新，使其具有在线动态修改参数的功能。先设定电机参数为正弦函数并进行微小变化，图4～图7是对时变参数的辨识效果。

图4 定子电阻辨识结果

图5 定子电感辨识结果

图6 转子磁链辨识结果

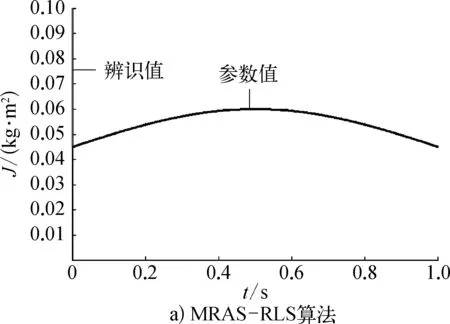
图7 转动惯量辨识结果

图4～图7中定子电阻、定子电感、转子磁链、转动惯量4个参数在MRAS-RLS算法中辨识前期波动都得到了较好的抑制，辨识值随着时间推移越来越接近设置值，辨识误差很小可以忽略。由于RLS算法随辨识时间的增加，修正效果越来越小，不会影响MRAS算法稳态过程的辨识结果，所以引入了MRAS-RLS算法，改善了辨识的动态过程，而稳态过程与普通的模型参数自适应相同。

在电机运行过程中，负载突然变化最容易引起电机转动惯量的突变。对于转动惯量的突变情况，运用MRAS-RLS算法和RLS算法的仿真模型，对转动惯量突变的情况进行仿真。在第0.3 s时使电机转动惯量从0.045 kg·m2突变到0.065 kg·m2，MRAS-RLS算法和RLS算法对转动惯量的辨识效果如图8所示。

图8 MRAS-RLS算法与RLS算法对转动惯量突变的辨识结果

如图8所示，转动惯量在第0.3 s突变的情况下，MRAS-RLS算法辨识值在第0.3 s有个突变；突变之后立即可以准确地辨识出参数的值，在时间上基本没有多少延迟，精确度基本也没有误差，证明MRAS-RLS算法对转动惯量在电机运行中突变的情况，可以很好地做出辨识。而RLS辨识结果在第0.3 s时有个微小的增加变化，但是变化很缓慢，直到第1 s时才接近0.065 kg·m2，辨识过程很长。由此可以看出RLS算法对于时变参数辨识效果不佳。

4 结束语

本文提出了用MRAS-RLS算法对PMSM参数进行辨识，经仿真分析验证MRAS-RLS算法对定常参数辨识的精度和速度都很高，对时变参数的辨识跟随性很好，证明了MRAS-RLS算法的改进效果良好。