运用零阶优化的吊钩参数化模型有限元分析

厉志安,唐 鸣,殷晓峰

(中国计量大学 质量与安全工程学院,浙江 杭州 310018)

起重机械广泛应用于港口、车站、车间装卸物料等生产场所,完成起重、运输、装卸和安装等工作,在经济生产中发挥重要作用。由于起重机械作业工作环境复杂多变,安全事故高发。吊钩作为起重机械的重要零部件,如果发生断裂损坏,将直接造成重大的安全事故,付出惨重的代价[1]。

吊钩在设计、使用和维护阶段存在弊端,在其设计过程中的理论计算只能通过经验公式计算某些特殊位置的应力,难以确定最危险的部位;使用过程中缺乏吊钩受力和形变的力学表征;维护阶段不能根据具体部位做出维修。因此吊钩在使用过程中的变形与损坏成为影响安全作业的重要原因。为了完成对起重机械关键零部件的力学分析,使用ANSYS、ABAQUS、PROE等计算机辅助工程软件是工程应用领域比较普遍的手段[2]。通过计算机辅助工程软件对起重机械零部件进行尺寸上的优化,实现减重与改善受力状态[3-6]。因此,根据有限元分析结果,对零部件的设计提出相应的要求,以保证起重机械的使用要求与安全性能。

相关学者通过对吊钩的实验与研究,指出了吊钩相关参数与其强度有着直接的关系[7-9]。但由于吊钩模型几何结构的非线性,致使理论公式计算误差较大,缺少对关键参数的优化设计,且普遍忽略了对实际工况下安全系数的考虑。基于以上,为了对吊钩进行全面的力学分析,通过ANSYS软件建立参数化模型,求解其在一定工况下的受力特性,结合计算结果与安全系数要求,完成强度校核分析。零阶优化方法作为ANSYS中通用的函数逼近方法,在粗优化阶段应用普遍,可以保证计算的效率且不易陷入局部极值点,能够有效地解决大多数工程问题。根据强度校核结果,针对相关参数,利用零阶优化中的子问题近似法与DV Sweeps法进行优化设计,能够使吊钩的强度性能得到一定提高,同时通过对设计参数的灵活控制还节省了吊钩材料。

1 模型的建立与分析

1.1 吊钩的结构及参数

以MMD型锻造吊钩为例,工作等级为M6,钩号为5,材质为Q345qD钢,弹性模量E=206 GPa,泊松比μ=0.28,下屈服强度335 MPa,抗拉强度490 MPa,密度7.85 g/cm3。在有限元分析中,材料特性参数的准确与否将在很大程度影响计算结果的真实程度[10]。其许用应力值[σ]计算如表1,其安全系数确定为1.65,由此得到许用应力为197 MPa。在实体模型中,确定了吊钩的各关键尺寸作为吊钩的模型参数,其几何参数如图1。其中吊钩钩孔直径D2为80 mm,水平截面A-A的尺寸B1为71 mm,H1为90 mm,垂直截面B-B的尺寸B2为60 mm,H2为75 mm。

表1 锻造吊钩的许用应力[σ][11]Table 1 Allowable stress of forged hooks[σ][11]

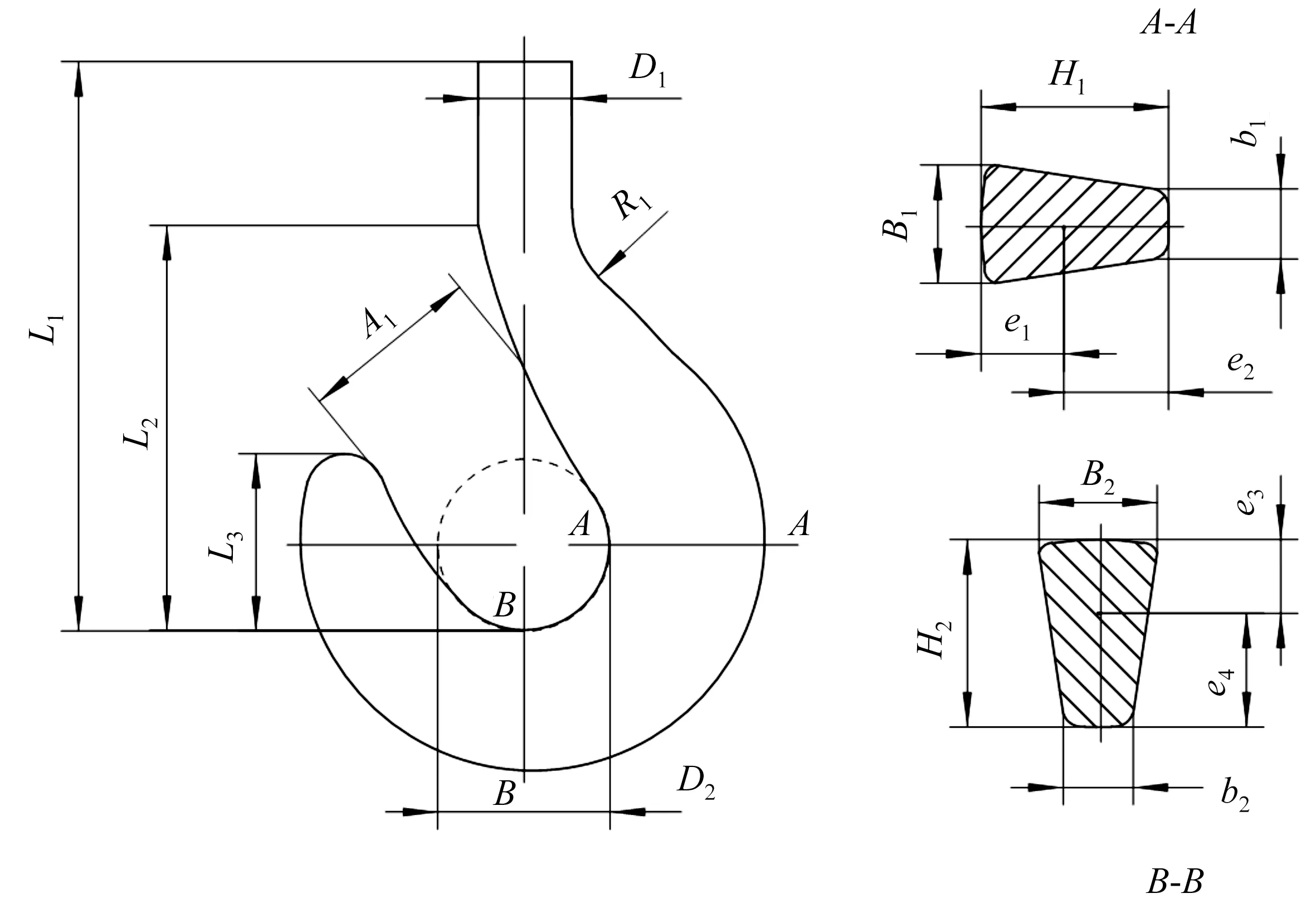
图1 MMD型吊钩几何参数Figure 1 MMD hook geometry parameter diagram

1.2 吊钩的危险截面理论计算

根据平面弹性曲杆理论的受力分析,通常将吊钩几何结构上的水平与垂直两个截面定义为危险截面。在理论计算中分析吊钩的两个危险截面,第一危险截面(A-A)受到的弯曲和拉伸组合应力最大,产生水平方向断裂;第二危险截面(B-B)处于直接受力区,应力集中,同时受到钢丝绳剧烈摩擦使其面积减小,吊钩的承载能力降低,容易产生垂直断面。吊钩危险截面的最大正应力相关计算如表2所示,其中Q为吊钩额定起重量(N),φ为动载荷系数,φ=1.6。

表2 吊钩危险截面的应力计算Table 2 Stress calculation of hook dangerous section

通过表2的计算可知,在两个危险截面上,吊钩内缘最大拉应力均大于外缘的最大压应力,且水平截面的最大拉应力略大于垂直截面的最大拉应力,为145.7 MPa,在安全范围内。但是,通过公式只能粗略计算极个别理论上危险位置的应力,并且由于几何近似,而实际的危险截面可能与计算存在较大误差,可靠度较低。

1.3 吊钩有限元模型的分析

针对上述模型,在ANSYS内完成几何建模,通过确定吊钩模型的约束关系,并对模型适度简化,从而建立吊钩的参数化模型。

选择Solid185八节点结构单元完成网格划分,为了提高分析精度,在两个危险截面附近区域进一步细化网格,最终单元数为10 321个。将约束条件定义为吊钩上端面的一个全约束(约束全部自由度)与吊钩垂直截面的一个对称约束,同时在吊钩内侧施加一个竖直向下的大小为50 kN的点载荷以模拟吊钩所受载荷。

1.4 计算结果与分析

求解得到有限元分析结果,根据第四强度理论,如式(1),得到Von Mises应力分布,其分布云图如图2。同时吊钩在受力后产生一定幅度的变形,其位移变形云图如图3。

(1)

其中σ2为主平面对应的主应力:σ1≥σ2≥σ3。

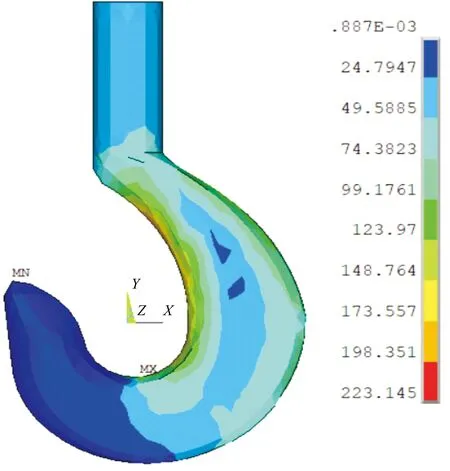
图2 吊钩Von Mises应力云图Figure 2 Von Mises stress of the hook

图3 吊钩位移变形云图Figure 3 Displacement and deformation of the hook

由图2可知,吊钩钩身内侧应力值大于外侧应力值,吊钩的最大Von Mises应力值位于钩身内侧,其最大应力值集中在198.4～223.1 MPa范围内,小于下屈服强度335 MPa。但结合安全系数考虑,等效应力值略大于其许用应力值197 MPa,故吊钩在该工况下处于相对危险的状态,一旦有内部缺陷或者裂纹等,吊钩将报废甚至发生安全事故,有必要进一步优化结构。

此外,吊钩在此工况下受到重物向下的拉应力,同时钩身的弯曲部分受到弯曲应力,结合对吊钩危险截面的理论计算,可以发现分析结果与表2中的计算存在一定误差,如以223.1 MPa计算,理论公式计算的相对误差约为34.7%。由于理论公式计算中对截面形状存在较大简化,故经验公式法不能全面真实反应吊钩实体模型表征力学性能,参考价值不大。

由图3可知,吊钩的最大位移形变处位于吊钩下端外侧靠前段位置,其最大形变量为1.1×10-5mm。由于吊钩受到重物拉应力与弯曲应力的作用,在吊钩钩身部分会产生一定程度不同大小的形变。在本工况下位移形变量较小,对吊钩工作影响程度有限,可忽略不计。

2 吊钩结构优化模型

ANSYS的分析结果显示在本例工况中吊钩的等效应力大于吊钩的许用应力值,不能充分满足安全性要求。针对吊钩的相关参数进行优化,在尽可能避免消耗多余材料的条件下,通过对吊钩相关参数的调整提高吊钩模型强度性能。由于吊钩的工作性质决定了它的宽度等相关尺寸不能再减小[12],在吊钩的模型参数中,吊钩危险截面的尺寸对吊钩的强度性能有着直接影响,于是选取吊钩的两个危险截面的尺寸参数进行优化,寻求提高吊钩模型的强度性能。

2.1 建立吊钩优化设计数学模型

基于最优化设计理论,根据设计所要求的性能目标,构建目标函数,在满足相应的约束条件下,通过对设计变量的优化选择,搜索确定目标函数的最大或最小值[13],数学模型可以表述为:

(2)

通过控制尺寸作为设计变量,在本例工况下把Von Mises最大应力值(SEQV_MAX)作为目标函数寻求其最小值,同时观察体积值(TVOL)的变化:

(3)

2.2 确定优化方法

ANSYS优化设计选用零阶优化方法中的子问题近似法结合DV Sweeps扫描法,可以得到多个优化后的设计序列结果。本方法只需要用到因变量值(目标函数与约束条件),而不需要用到其导数值,从而减小计算时间。因变量首先以最小二乘拟合方法被近似地取代,同时通过对目标函数等施加罚函数将受约束的最小化问题转化为无约束问题[14],即

(4)

(5)

式(5)中,F(x,pk)为新无约束优化的目标函数,f0为参考目标函数数值,pk为响应面参数,X、G分别为设计变量与状态变量的罚函数。

3 结 果

ANSYS优化设计选用零阶优化方法结合DV Sweeps扫描法,可以得到多个优化后的设计序列结果。对设计序列结果进行筛选,表3给出了初始设计序列与设计序列结果中的8个最佳设计序列,其中序号9的序列为本次优化的最优解,其目标函数值最小并实现了总体积的减小。取最优解时各设计变量参数为:吊钩水平截面A-A尺寸B1为70.80 mm,H1为88.68 mm,垂直截面B-B尺寸B2为59.72 mm,H2为68.90 mm。

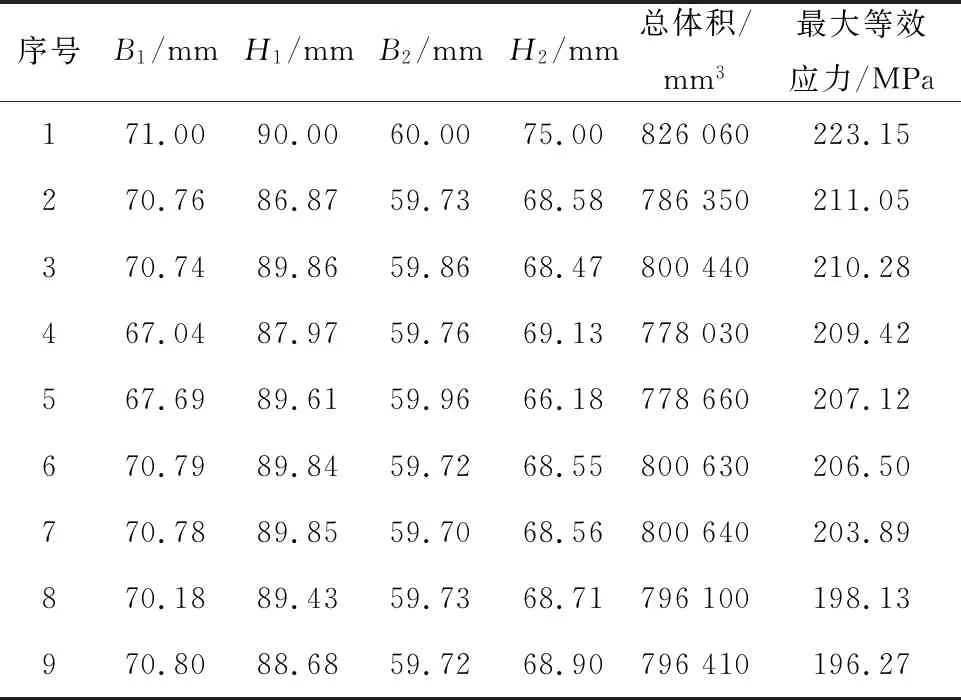
表3 优化设计序列Table 3 Sequence of the optimization design

从表3可以看出,经过尺寸优化后模型目标函数值明显减小,最大等效应力相较于原始尺寸的223.1 MPa减小至196.27 MPa,低于许用应力197 MPa,减小了12%,符合其强度要求。

同时总体积大小也降低了4%,在提高吊钩模型的强度性能的条件下实现了材料的节省。优化设计后的吊钩Von Mises应力云图与位移变形云图如图4和图5,其最大应力值小于许用应力,最大位移形变为1.1×10-5mm,满足吊钩设计的强度要求。

图4 优化后的吊钩Von Mises应力云图Figure 4 Optimized Von Mises stress of the hook

图5 优化后的吊钩位移变形云图Figure 5 Displacement and deformation of the optimized hook

4 结 论

针对起重机械MMD型吊钩利用ANSYS建立参数化模型,通过有限元分析得到了在规定工况下所建立的吊钩模型的应力与变形分析结果。同时结合对吊钩两个危险截面应力的理论计算,对吊钩的强度性能及其安全性的要求进行了讨论与判断。为了使吊钩满足强度要求,基于ANSYS优化设计零阶优化方法中的子问题近似法结合DV Sweeps扫描法,得到多个优化结果并找到了最优解,吊钩最大应力下降了12%,材料节省4%,有效地达到了提高吊钩模型的强度性能的目的,同时实现了模型材料的节省,为吊钩的设计、使用维护提供了一定的指导。同时,本方法计算过程简单,也能进一步推广至其类型吊钩、甚至其他关键部件的优化设计。