自制片式吊钩可靠性分析

范亚栋 刘文娟 张淑敏

一、引言

吊钩是起重作业中应用最广泛的取物装置，它承担着吊运物体的全部载荷，是起重设备安全生产三大构件（制动器、钢丝绳和吊钩）之一。吊钩一旦损坏极易造成重大的人身伤亡事故。因此对吊钩进行危险截面处的应力情况进行分析是十分必要的，尤其是公司基于生产实际情况，会自制一些非标式吊钩，其设计及使用过程的可靠性验证尤为重要。

二、自制片式吊钩的结构及曲梁理论计算

1、吊钩的结构及参数

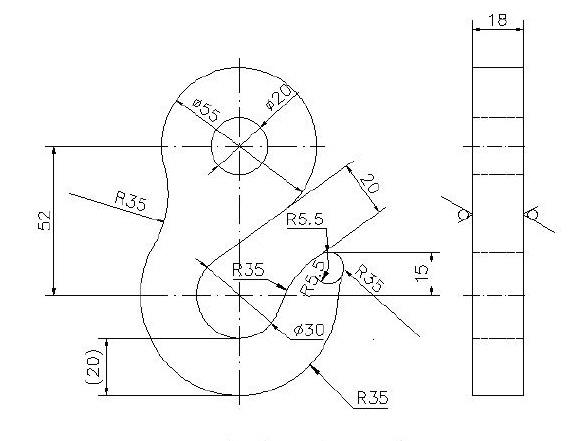
以河北华北柴油机有限责任公司总装分厂用KF95.038水冷发动机整机吊具中的吊钩部分为研究对象，其结构尺寸如图l所示。

此吊钩为分厂自制片式吊钩，配合使用的部件包括吊环、吊板和连环等组成，吊具三维模型及其使用环境模型见图2和图3所示。

吊钩零件选用的材料为45#钢，其材料选择及主要力学参数见表l所列。

2、按照曲梁理論计算吊钩危险断面的受力分析

按照GB/T10051.1-2010中吊钩第1部分：力学性能、起重量和应力及材料的相关说明，确定出吊钩的危险截面有两个，即A-A水平截面，B-B垂直截面，如图4所示。

（1）A-A水平截面受力分析。

此截面的理论受力情况分为两部分，被吊物体在竖直方向产生的拉伸力Q;在钩口内侧由拉应力Q产生的弯曲应力，弯曲应力的表现形式是吊钩的背口端产生了被拉直的趋势，即C点产生拉应力，D点产生压应力，拉应力比压应力的绝对值大一倍多。该截面的最大应力详尽计算公式如下：

式中，σ是截面的拉应力，单位为MPa;是拉伸力，单位为N;F是截面面积，单位为mm²;R₀是截面重心轴线至曲率中心点距离，单位为mm;W_Ay是截面对于垂直y轴抗弯模量;K_B是依截面形状确定的曲梁系数。

在实际工程应力分析过程中，一般可直接得到吊钩的各项设计尺寸数值，如图4。这使得我们可根据式2、式3直接对危险截面的最大受力点进行应力计算。

式中，σ_c是C点的拉应力，单位为MPa;σ_D是D点的压应力，单位为MPa;e₁是截面中心至内缘距离，单位为mm;e₂是截面中心至外缘距离，单位为mm。

（2）B-B垂直截面受力分析。

钩身垂直截面B-B受力虽不如 A-A截面大，但却是吊钩提升过程中被钓物体直接作用的承力点，受剪切应力，其计算公式如下：

式中，Q是拉伸力，单位N;F_B-B是截面面积，单位mm²。

（3）起升动载荷系数。

在货物吊运过程中，吊钩经历了货物的起升离地、运送及达到指定位置后将货物降至地面三个阶段。货物的起升离地过程中，吊钩由无负载状态变为负载状态，此过程时间极短，货物由于自重原因产生的惯性力使得吊钩及被吊货物同时产生了弹性振动，因此在一般提升拉伸力计算过程中要同时考虑被吊货物的铅垂惯性力和振动力。因此，本文分析过程引入起升动载荷系数φ，结合吊具的实际使用过程，起升装置运行较为平稳，速度较缓，直接取φ=1.1，即：

Q=ψMg （5）

3、危险断面的受力计算

按照吊具设计起吊最大重量1600Kg，计算A-A水平截面C、D两点及B-B垂直截面受力情况，验证其是否可靠。为简化计算过程，我们选取单吊钩吊重800Kg为具体算例进行计算。

对于矩形截面曲梁的截面形状系数的计算公式如下：

式中，a是吊钩钩口直径，单位为mm，本例取值30mm;h是截面高度，单位为mm，本例取值18mm。带入相应数值求得：

三个力均小于屈服强度σ。因此，吊钩工作时处于安全状态。

三、有限元模型的建立与分析

本文的前述章节已利用弹性力学理论直观的描述了吊钩工作状态中所受到的应力情况，过程较为复杂。现今，工程技术人员已经广泛采用有限元法对吊钩进行分析，从而实现应力、应变等问题的计算求解，确保其满足工程使用要求。本节应用现代有限元分析方法，对吊钩的强度进行分析，发现吊钩的最大变形位置及所受应力情况。

1、有限元分析步骤

有限元法的基本思想是离散化，“先分后台”，其实质是将求解连续体问题转化为求解离散单元体的组合问题，对单元进行分析，得到以节点位移为未知数的线性方程组，用消元法或迭代法求出位移的近似值，得到各节点的应力值，从而再得到整个连续体的近似值。PTC公司开发的有限元分析软件Pro/MECHANICA模块（简称Pro/M）可完全集成于Pro/ENGINEER环境中，用户可在CAD模型构建后，不脱离Pro/ENGINEER环境就能对几何模型进行有限元分析。具有边界条件处理简单，界面柔和，运算精度高的特点。Pro/MECHANICA分析步骤如图5所示。

2、吊钩模型简化及有限元分析

（1）几何模型的简化及材料属性设定。

某些过渡几何特征对结构件强度的影响很小，在Pro/MECHANICA中这些几何特征会增加畸变网格的产生几率，增加计算时间，影响计算精度。鉴于本文以吊钩钩口端为研究重点，分析其受力环境中的应力应变状況，且在相关的文献研究中，绝大多数忽略了倒角、吊钩钩耳（非危险断面）的影响，故对其做简化处理。同时按照表l中45#钢的相关力学性能参数，对其做属性配置。简化后模型如图6所示。

（2）网格划分及边界条件处理。

单元分析作为有限元分析的基础，单元类型的选择和网格划分的精细程度，影响了计算的准确性。因吊钩钩口端形状不规则，为提高运算速度，保证计算精度，直接选取“最大元素尺寸”缺省网格控制类型来定义创建网格，根据需要自定义全局单元尺寸大小为2mm，共计形成四面体单元数为40857个，如图7所示。

模型本身在没有约束的情况下，任意单元的8个节点处于自由状态，所以必须引入位移边界条件。约束施加于最上端平面，假设吊钩在工作中只能沿Y轴旋转，定义约束时将该端面除Y轴旋转自由度外，其余5个自由度完全固定。

在分厂实际的吊装过程中，被吊整机经常性发生摆动，故吊钩的实际受力方向会偏离垂向一定角度，根据工程经验，夹角应控≤20°。因此，偏角20°时，吊钩处于最不利载荷的极限工况。已知载荷的作用面区段约为发动机整机吊环直径与吊钩厚度的乘积，发动机整机已装吊环直径为28mm，得：

载荷作用面为通过吊钩中间竖直平面两侧各20°。

约束及载荷施加完成后效果如图8所示。

（3）吊钩静态结构应力及位移分析。

边界条件精确定义后，对吊钩进行有限元分析，得到其在最大载荷作用工况环境中的应力、应变分布图，实现模型静态结构应力及位移分析。

图9是由Pro/MECHANICA模块直接模拟吊钩真实工作环境后測算的模型所受应力图，从图中可以得到，吊钩起吊发动机时，吊钩的最大VonMises等效应力σ_max=299.7MPa，发生位置基本与C-C截面保持一致，在吊钩弯曲圆弧内侧区域，且σ_max<σ_s。

为深入研究吊钩所受应力的分布形式，确保吊钩结构的可靠性，本文基于与图9相同的边界条件处理方式，对吊钩应力以“等值面”及“切割曲面”两种类型进行分析。图10中左侧表示将吊钩所受应力分为了A-I九级，右侧表示以WCS坐标系定义方式，在Z轴垂向深度的50%处做切片曲面，应力在此曲面上的分布情况。左侧图中各等值面片层基本保持平行，说明吊钩工作时所受应力分布均匀。在边缘倒角处、钩头或吊耳连接等处偶有等值面突起或分叉现象，说明此处应力分布出现分散，其实质原因是该处截面形状急剧变化所致，但从图中云图颜色可以看出，此处应力在较低值，不会对吊钩的可靠性产生影响;分析右侧图得出，虽然吊钩内外侧边缘处所受应力差异较大，但其变化趋势基本一致，即吊钩钩体中性层应力最低，然后随离中性层距离的增大而增大，呈“V”型分布状态。

因此可以得出结论，此吊钩结构合理，所受应力分布均匀，具有较高的可靠性。

图11是由Pro/MECHANICA模块直接模拟吊钩真实工作环境后测算的模型发生的位移示意图，其中透明部分为吊钩的原位置，色带表示了不同的位移值。从图中可以得到，吊钩起吊发动机时，吊钩的最大位移σ_max=0.313mm，发生在钩头外侧。

图12为吊钩位移沿最外侧圆弧曲线在X、Y、Z三个方向的分量值，由图可以观察出，X向最大分量为σ_xmax=0.190mm，Y向最大分量为σ_ymax=0.312mm，Z向最大分量为σ_zmax=0.003mm，均發生在圆弧曲线160mm处（即钩头外侧位置）。

因此可以得出结论，此吊钩处于工作状态时，发生位移的偏移数值较小，基本可忽略不计，三轴向分量均在材料弹性变形量范围内，吊钩满足使用要求。

四、结论

本文从吊钩结构的静强度入手，通过弹性曲梁理论、极限承载理论对实际工况环境中，吊钩危险截面处所受的应力进行分析计算，并在Pro/M软件中分析了吊钩在最大负载下应力分布及位移情况，揭示其应力分布规律。两种机械可靠性分析方法对吊钩得出的应力、位移分析数值基本一致，互相验证了其正礆性。此分析方式为吊钩设计及使用过程可靠性分析提供了借鉴意义。