爆炸荷载下RC深梁的动力响应及破坏形态∗
周清 孙亮 刘海员
(滨州市规划设计研究院 256600)
引言
众多学者对爆炸荷载作用下RC 普通梁的动力响应及破坏进行了深入的研究。 蔡路军[1]采用试验的方法研究了爆炸荷载下RC 梁的应变与损伤。 匡志平[2]采用试验的方法研究了爆炸荷载下普通RC 梁破坏形态。 田力[3]采用数值分析的方法研究了RC 梁在冲击波与破片联合作用下的动态响应。 张秀华[4]采用数值分析的方法对爆炸荷载作用下RC 梁的动力响应和破坏过程进行了分析。 T.Krauthammer 等[5]基 于 Timoshenko 梁 理论,考虑了钢筋和混凝土的材料非线性和应变率效应,提出了RC 梁在均布爆炸荷载下动态响应的简化数值分析方法。 M.Barbato[6]提出了一种简单高效的二维有限元模拟方法,能够准确预测FRP 加固的 RC 梁的抗爆承载力。 Ghabossi 等[7]应用有限元技术对爆炸试验结果进行了数值模拟。 以上学者研究的对象均为RC 普通梁,对于RC 深梁并未涉及。 国内外均将跨高比<2 的RC简支梁及跨高比 <2.5 的RC 连续梁视为深梁,其受力性能及配筋方式与普通梁有很大的区别。目前国内外相关文献中尚未发现专门针对RC 深梁抗爆试验研究,笔者在以往学者对RC 普通梁抗爆研究[8,9]的基础上,借助于 LS-DYNA 软件,采用数值分析的方法对爆炸荷载作用下RC 深梁的动力响应与破坏形态进行分析。
1 爆炸荷载作用下RC普通梁抗爆数值分析验证
李猛深[8]通过对比数值分析与试验结果,验证了数值分析方法的正确性。 汪维[9]只进行了试验,并未进行数值分析验证。 为进一步验证钢筋J-C 模型[10]与混凝土KCC 模型[11]在抗爆数值分析中的准确性,利用LS-DYNA 软件建立与文献[9]中框架梁完全相同的有限元模型,试验结果与数值分析结果如图1 所示。 通过对图1 分析可知,爆炸荷载作用下RC 普通梁发生较为严重的破坏,梁破坏范围主要集中在爆炸点下方,以弯曲破坏为主,而支座处的剪切破坏程度较小。 试验后测量得到的梁跨中破坏长度约为1000mm[9],而数值分析得到的梁跨中破坏长度为945mm,误差为5.5%。 试验后测量得到的梁跨中最大位移为240mm[9],数值分析得到的梁跨中最大位移为228mm,误差为5%。 通过对比可知,数值分析计算得到的结果误差较小,与试验结果非常接近。

图1 试验结果与数值分析结果对比(Z=0.464kg/m1/3)Fig.1 Comparison of experimental results with numerical analysis results(Z=0.464kg/m1/3)
2 爆炸荷载作用下简支单跨RC深梁的动力响应与破坏形态
2.1 简支单跨RC深梁方案及有限元模型
在文献[9]研究的基础上,对简支单跨RC深梁进行分析。 采用与文献[9]相同宽度、相同跨度、相同配筋率的RC 梁,通过改变梁高度使其成为深梁,以研究其在不同比例距离爆炸荷载作用下的动力响应与破坏形态。 爆炸力学采用比例距离Z即爆炸点至结构的距离R与药量W的立方根之比Z=R/W1/3作为单位衡量爆炸产生的超压作用。 炸药采用 10kg、50kg 标准 TNT,爆炸点位于跨中梁顶上方1m,比例距离分别为Z=0.464kg/m1/3、0.271kg/m1/3。 RC 深梁跨度与高度的比值l0/h称作跨高比,跨高比不同的梁破坏形态有所不同。 《混凝土结构设计规范》(GB50010 -2010)[12]规定,简支 RC 单跨深梁应将纵向受拉钢筋布置在梁下边缘0.2h的范围内。据此设计出4 种不同跨高比RC 深梁方案见表1。

表1 简支单跨RC 深梁方案Tab.1 Simply supported RC deep beam schemes
利用LS-DYNA 软件建立上述4 种方案的有限元模型,钢筋、混凝土材料分别采用 J-C 模型、KCC 模型,添加关键字∗MAT_ADD_EROSION 定义混凝土材料的破坏,采用最大主应变作为失效准则。
炸药采用高能炸药材料∗MAT_HIGH_EXPLOSIVE_BURN 模型配合 JWL 方程定义。 以炸药爆轰产物的压力表示的JWL 方程[13]为:

式中:Pa为爆炸压力;V为相对体积;E0为初始内能密度;A、B、R1、R2、ω为状态方程参数,其具体数据见表2[13]。

表2 炸药材料参数与状态方程参数Tab.2 TNT material parameters and equation of state parameters
空气材料采用∗MAT_NULL 配合∗EOS_LINEAR_POLYNOMIAL 状态方程定义,线形多项式状态方程[13]为:

式中:Pb为空气压力;μ表示空气的相对体积,μ=(1/V) -1;C0~C6为多项式方程系数;E为内能密度。 各相关参数取值见表3[13]。

表3 空气材料参数与状态方程参数Tab.3 Air material parameters and equation of state parameters
炸药与空气定义为多物质欧拉几何实体(EULER),混凝土定义为拉格朗日几何实体(LAGRANGE),采用流固耦合的方式(ALE 方法)定义爆炸波与结构体之间的接触[14]。 利用关键字∗DEFINE_CURVE 配合关键字∗LOAD_BODY_Y定义RC 梁竖直方向的重力,重力加速度取值9.81m/s2。 利用关键字∗RIGIDWALL_PLANAR定义刚性地面以考虑爆炸波的反射作用[15]。
图2 为简支单跨RC 深梁示意及有限元模型。为了便于研究RC 深梁不同位置钢筋应力,采用分离式建模,即钢筋与混凝土分别单独建立模型,按照实际的钢筋直径与长度建立钢筋有限元模型。 由于爆炸荷载作用时间很短,爆炸荷载下混凝土与钢筋可以保持变形协调,所以采用共用节点的方式实现钢筋与混凝土单元的接触。 单元网格尺寸大小对于数值分析结果会产生一定的影响,网格过大会影响计算精度,网格过小不仅对提高计算结果精度有限而且还会成倍地增加计算时间。 根据文献[16]的建议,炸药、空气、混凝土、钢筋单元均取值20mm,使用此网格尺寸不仅可以得到较为精确的计算结果并且不会花费过高的计算成本。
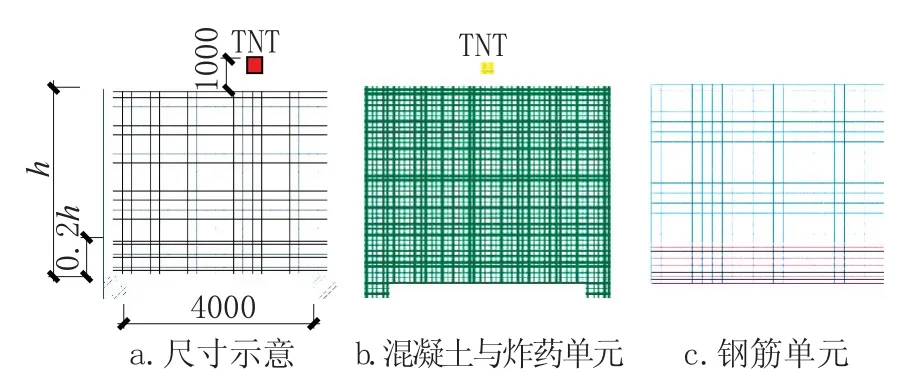
图2 简支单跨RC 深梁示意及有限元模型Fig.2 Simply supported RC deep beam diagram and finite element model
2.2 Z=0.464kg/m1/3爆炸荷载作用下简支单跨RC深梁的破坏形态及动力响应
图3 为不同方案简支单跨RC 深梁在Z=0.464kg/m1/3爆炸荷载作用下的塑性破坏图。 与图1 对比可知,相同比例距离爆炸荷载作用下的RC 深梁比普通梁破坏程度小的多,这主要是因为深梁的刚度较大、抗爆能力更强。 跨高比l0/h=2.5(方案1)深梁的塑性分布区域主要集中在爆炸点正下方的梁顶与跨中梁底部位且梁底部分布更大。 随着跨高比的减小,梁底塑性区域迅速减少,跨高比l0/h=1.0(方案4)时仅在跨中梁底很小的范围内出现塑性区域。

图3 Z=0.464kg/m1/3爆炸荷载作用下不同方案简支单跨RC 深梁塑性图Fig.3 Plasticity diagrams of RC deep beam under blast load with Z=0.464 kg/m1/3
简支单跨深梁下部纵向钢筋主要布置于底部0.2h范围内,深梁的高度较大使得底部纵筋0.2h配筋范围较RC 普通梁大的多。 为研究不同部位梁底纵筋应力,选取配筋范围内底部(0 ~1/3 配筋范围)、中部(1/3 ~ 2/3 配筋范围)、上部(2/3 ~1 配筋范围)共3 条最大纵筋应力曲线进行分析。 图4 为Z=0.464kg/m1/3爆炸荷载作用下跨高比l0/h=2.5(方案1)与跨高比l0/h=1.0(方案4)的3 条应力曲线,分析图4 可知:当跨高比l0/h=2.5 时,底部纵筋与上部纵筋以拉应力为主,应力峰值约为600MPa; 中部纵筋首先受拉,然后受压,拉应力约为 500MPa,压应力约为600MPa。 考虑应变率效应时的钢筋应力应有所提高[10],此时考虑应变率效应的钢筋最大应力为钢筋极限强度(570MPa)的1.05 倍左右。 当跨高比减小为l0/h=1.0 时,底部、中部、上部纵筋均产生拉应力,且底部纵筋最大拉应力为280MPa,远高于中部与上部纵筋拉应力且小于钢筋的极限强度。 以上说明,Z=0.464kg/m1/3爆炸荷载作用下随着跨高比l0/h的减小,梁底配筋范围内纵筋发挥程度越来越小。
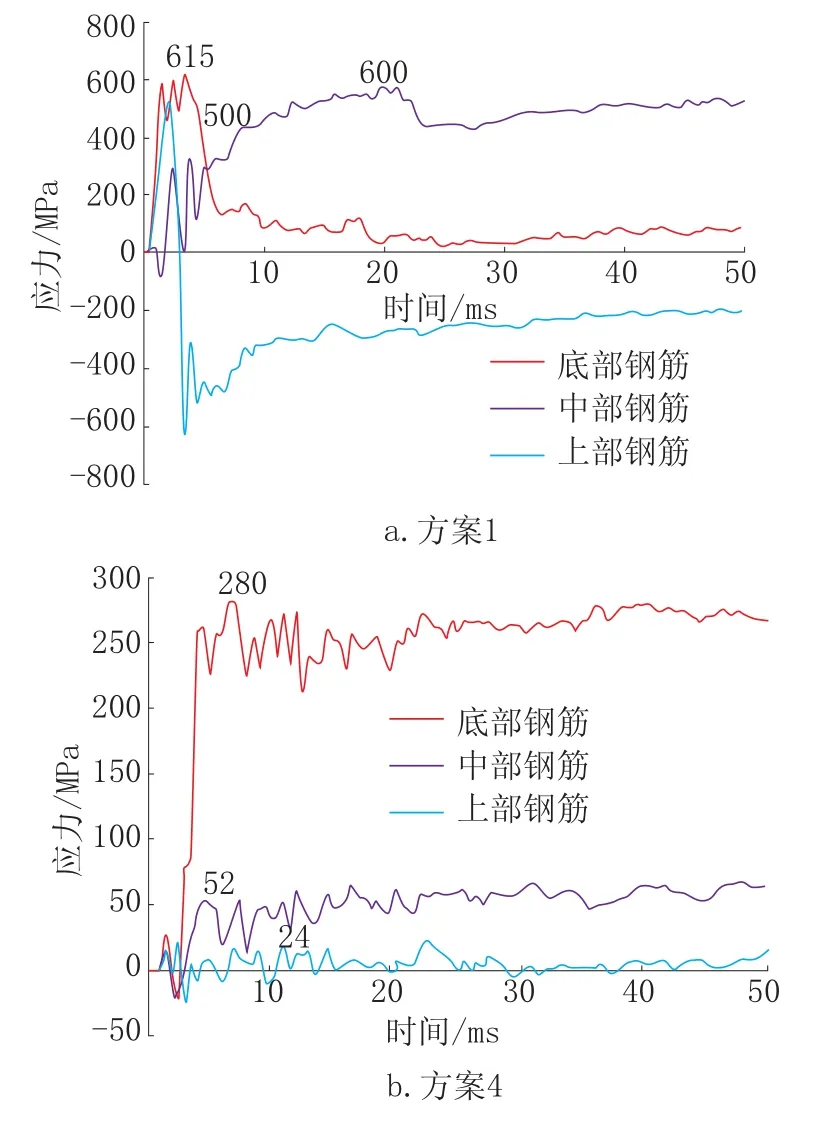
图4 Z=0.464kg/m1/3爆炸荷载作用下不同方案简支单跨RC 深梁梁底不同位置纵筋应力曲线Fig.4 Stress curves of longitudinal steel bars of RC deep beam under blast load with Z=0.464kg/m1/3 in different positions
图5 为不同方案RC 深梁在Z=0.464kg/m1/3爆炸荷载作用下的跨中最大位移,分析图5 可知,由于深梁的刚度较大而使得跨中最大位移很小。 当l0/h=2.5(方案1)时,跨中最大位移为18mm。 跨中最大位移随着跨高比l0/h的减小而迅速减小,当l0/h=1.0(方案4)时,位移仅为4mm。

图5 Z=0.464kg/m1/3爆炸荷载作用下不同方案简支单跨RC 深梁跨中最大位移Fig.5 Middle cross displacement curves of RC deep beam under blast load with Z=0.464kg/m1/3
2.3 Z=0.271kg/m1/3爆炸荷载作用下简支单跨RC深梁的破坏形态及动力响应
将炸药药量W增大至50kg,位置保持不变,此时比例距离Z=0.271kg/m1/3,研究简支单跨RC 深梁在较大爆炸荷载下破坏情况。 图6 为不同方案简支单跨RC 深梁在Z=0.271kg/m1/3爆炸荷载作用下塑性破坏图。 分析图6 可知:梁发生严重破坏,当跨高比l0/h=2.5(方案1)时,主要破坏形式为梁底的弯曲破坏,表现为梁底混凝土分层发生断裂,梁底大量纵筋被拉断。 随着跨高比的减小,梁底弯曲破坏逐渐减小而支座处的剪切破坏逐渐增加,当跨高比l0/h=1.0(方案4)时,支座发生严重的剪切破坏,支座上部大量混凝土因破碎而脱离梁主体。
图7 为Z=0.271kg/m1/3爆炸荷载作用下跨高比l0/h=2.5(方案1)与跨高比l0/h=1.0(方案4)的3 条应力曲线,分析图 7 可知:当跨高比l0/h=2.5 时,全范围的底部纵筋最大应力均超过钢筋的极限强度且数值大致相等(约800MPa),考虑应变率效应的钢筋最大应力为极限应力的1.40 倍。 当纵筋到达最大应力后迅速衰减,t=40ms 左右纵筋被拉断,应力变为零。 随着高跨比的减小,纵筋最大应力随之迅速降低,且配筋范围内中部与上部纵筋较底部纵筋降低更快。 当跨高比l0/h= 1.0 时,底部纵筋最大应力为610MPa,略高于极限强度。 此时上部与中部配筋范围内纵筋的最大应力降至200MPa ~300MPa。 图8 为不同方案RC 深梁在Z=0.271kg/m1/3爆炸荷载作用下跨中梁底截面发生破坏时的位移时程曲线。曲线的斜率k可以反映其破坏程度,斜率k越大梁破坏越严重。 通过图8 可知,跨高比l0/h=2.5、2.0 的梁发生严重破坏其破坏程度接近,当跨高比l0/h减小至1.5 以下时梁破坏程度明显降低。

图6 Z=0.271kg/m1/3爆炸荷载作用下不同方案RC 深梁塑性破坏图Fig.6 Plasticity diagrams of RC deep beam under blast load with Z=0.271kg/m1/3
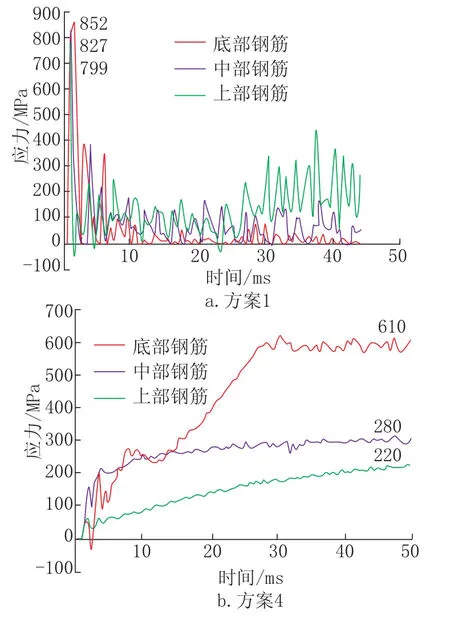
图7 Z=0.271kg/m1/3爆炸荷载作用下不同方案简支单跨RC 深梁梁底不同位置钢筋应力曲线Fig.7 Stress curves of longitudinal steel bars of RC deep am under blast loadwith Z=0.271kg/m1/3 in different positions

图8 Z=0.271kg/m1/3爆炸荷载作用下不同方案简支单跨RC 深梁跨中最大位移时程曲线Fig.8 Middle cross displacement curves of RC deep beam under blast load with Z=0.271kg/m1/3
3 爆炸荷载作用下简支连续RC深梁的动力响应与破坏形态
3.1 简支连续RC深梁方案及有限元模型
建立连续深梁为2 跨,每跨的跨度为4m。爆炸点分别取支座梁顶截面以上1m(爆炸点1)与某跨跨中截面以上1m(爆炸点2),药量取10kg 与50kg,比例距离分别为Z=0.464kg/m1/3、0.271kg/m1/3。 《混凝土结构设计规范》规定,连续深梁的中间支座截面的纵向受拉钢筋应根据不同跨高比按照不同的比例布置于支座顶面以下0.8h的范围内。 据此设计不同跨高比l0/h=2.0、1.25、0.8 共3 种简支连续RC 深梁方案,分别对应图9b的3 种不同的配筋形式,梁配筋率仍取值1.2%。采用与2.1 节简支单跨RC 深梁相同的建模方法,得到的简支连续RC 深梁方案如表4 所示。

图9 简支连续RC 深梁尺寸及支座配筋方式Fig.9 Size and reinforcement model of simply support continuous RC deep beam

表4 简支连续RC 深梁方案Tab.4 Simply support continuous RC deep beam schemes
3.2 Z=0.464kg/m1/3爆炸荷载作用下简支连续RC深梁的破坏形态及动力响应
图10 为Z=0.464kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁塑性图。 分析图10 可知:相同比例距离爆炸荷载作用下相对于简支单跨RC 深梁,连续深梁破坏程度更小。 跨高比l0/h=2.0(方案1)、爆炸点1 时,出现塑性的主要区域为梁支座处; 爆炸点2 时,出现塑性的主要区域为爆炸点正对的梁底。 无论爆炸发生在爆炸点1 或爆炸点2,随着跨高比l0/h的减小,梁塑性区域均明显减少。 跨高比减小至l0/h=0.8(方案3)时,仅在中间和边跨支座处出现非常小的塑性区域。

图10 Z=0.464kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁塑性图Fig.10 Plasticity diagrams of RC deep beam under blast load with Z=0.464kg/m1/3
连续RC 深梁配筋形式较为复杂,按照不同位置采集得到的不同方案、不同爆炸点纵筋最大应力汇总为表5。 通过表5 可知:Z=0.464kg/m1/3爆炸荷载作用下各工况纵筋应力均远小于极限应力。不同爆炸点的钢筋最大应力均为跨高比l0/h=2.0(方案1)的梁底纵筋,但位置不同:爆炸点1 时为中间支座截面,数值为44.6MPa; 爆炸点2 时为爆炸点正对的跨中截面,数值为61.3MPa。

表5 Z=0.464kg/m1/3爆炸荷载作用下不同位置纵筋最大应力(单位:MPa)Tab.5 Maximum stress of longitudinal steel bars under blast load with Z=0.464kg/m1/3 in different positions(unit:MPa)
3.3 Z=0.271kg/m1/3爆炸荷载作用下简支连续RC深梁的破坏形态及动力响应
图11 为Z=0.271kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁塑性破坏图。 分析图11可知:(1) 爆炸发生在爆炸点 1 时,跨高比l0/h=2.0(方案1)的梁中间支座发生严重的剪切破坏,破坏范围延伸至两侧跨中梁底。 随着跨高比的减小,中间支座的剪切破坏程度逐渐降低而边支座的剪切破坏程度逐渐增加; (2)爆炸发生在爆炸点2 时,破坏范围主要集中在爆炸点所正对的梁,相邻梁的破坏程度较小。 跨高比l0/h=2.0(方案1)的梁底发生严重的弯曲破坏,破坏特征与简支单跨梁相似。 随着跨高比的减小,梁弯曲破坏逐渐降低而边跨支座处的剪切破坏逐渐增加。
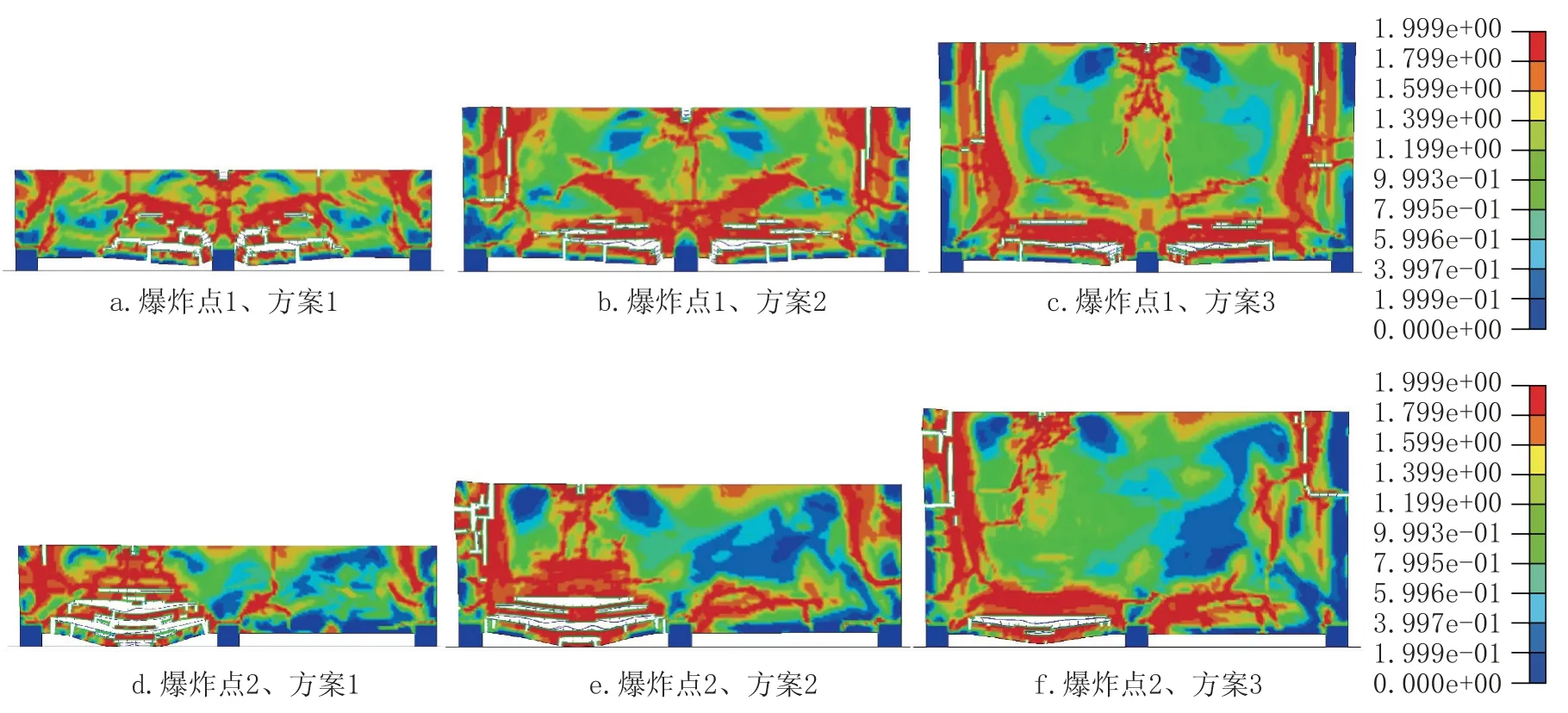
图11 Z=0.271kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁塑性破坏图Fig.11 Plasticity diagrams of RC deep beam under blast load with Z=0.271kg/m1/3
表6 为Z=0.271kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁不同位置纵筋最大应力表。 分析表6 可知:(1)爆炸发生在爆炸点1 时,跨高比l0/h=2.0(方案1)梁底纵筋最大应力出现在支座截面。 考虑应变率效应的梁底钢筋最大应力为860MPa,约为极限强度的1.51 倍。 中间支座的纵筋最大应力均超过极限强度且大致相等,约为700MPa。 随着跨高比l0/h的减小,梁底纵筋最大应力与中间支座0 ~0.4h范围内的最大纵筋应力基本保持不变而中间支座0.4h~0.8h范围内的最大纵筋应力迅速降低。 当跨高比l0/h=0.8(方案3)时,中间支座 0.4h~0.8h范围内的最大纵筋应力仅为136MPa; (2)爆炸发生在爆炸点2 时,跨高比l0/h=2.0(方案1)梁底纵筋最大应力出现在爆炸点正对的跨中截面。 考虑应变率效应的梁底最大纵筋应力为855MPa,约为极限强度的1.50 倍。 中间支座纵筋应力均远小于极限应力。 随着跨高比l0/h的减小,所有纵筋最大应力均逐渐减小并且中间支座纵筋最大应力远小于梁底。 当跨高比l0/h=0.8(方案3)时,梁底纵筋最大应力为671MPa,约为中间支座最大纵筋应力的10 倍。

表6 Z=0.271kg/m1/3爆炸荷载作用下不同位置纵筋最大应力(单位:MPa)Tab.6 Maximum stress of longitudinal steel bars under blast load with Z=0.271kg/m1/3 in different positions(unit:MPa)
图12 为Z=0.271kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁的位移时程曲线。 通过图12 可知,爆炸发生在爆炸点1 时破坏最严重的位置为中间支座截面,爆炸发生在爆炸点2 时破坏最严重的位置为爆炸点正对的跨中截面。 曲线的斜率k随着跨高比的减小而减小,说明深梁随着跨高比的减小破坏程度逐渐降低。

图12 Z=0.271kg/m1/3爆炸荷载作用下不同方案简支连续RC 深梁位移时程曲线Fig.12 Displacement curves of RC deep beam under blast load with Z=0.271 kg/m1/3
4 结论
1.不同比例距离爆炸荷载作用下简支单跨RC 深梁的动力响应与破坏形态:Z=0.464kg/m1/3时简支单跨RC 深梁处于弹性振动阶段,随着跨高比l0/h的减小梁底各部位的纵筋最大应力迅速减小,梁破坏程度较小。Z=0.271kg/m1/3时简支单跨RC 深梁发生严重的塑性破坏,随着跨高比l0/h的减小,梁由跨中梁底弯曲破坏为主逐步变为支座剪切破坏主。
2.不同比例距离爆炸荷载作用下简支连续RC 深梁的动力响应与破坏形态:Z=0.464kg/m1/3时,简支连续梁破坏程度较简支单跨梁更小,梁底纵筋与支座各范围的纵筋最大应力均远小于钢筋的极限强度。Z=0.271kg/m1/3时爆炸点发生在支座梁顶上方,连续深梁主要发生中间支座与边支座的剪切破坏。Z=0.271kg/m1/3时爆炸点发生在某跨跨中梁顶上方,爆炸波主要对该跨梁产生较大的作用,对相邻梁影响较小。 此时,该跨梁以梁底弯曲破坏为主。 无论爆炸点发生在何位置,随着跨高比l0/h的减小,梁破坏程度均逐渐降低。

