基于DEA的投入产出效率评价系统设计与实现

徐齐利

（江西财经大学 经济学院 江西 南昌 330013）

一、引言

对于经济分析和管理决策中的系统评价问题，1978年，运筹学家Charnes和Cooper提出一种数据包络分析方法（Data Envelopment Analysis，DEA），用于在具有多项投入指标、多项产出指标的同类型生产单元之中，评价具体某个生产单元其投入产出的相对有效性。自此，投入产出DEA效率评价便在经济分析和管理决策的诸多领域具有非常广泛的应用。

在DEA的发展历程中，致力于管理科学研究的理论运筹学家在投入产出效率DEA评价的模型开发方面已取得长足进步[1-3]；相比之下，致力于管理工程研究的应用运筹学家在投入产出效率DEA评价的系统开发方面却一直难有起色。鉴于此，本文作者在MATLAB平台上开发的一款基于DEA的投入产出效率评价系统。

系统的功能主要有：（1）投入效率评价，具体包括投入的综合效率测度与评价、投入的技术效率测度与评价、投入的规模效率测度与评价、投入的超效率测度与评价及投入效率汇总评价；（2）产出效率评价，具体包括产出的综合效率测度与评价、产出的技术效率测度与评价、产出的规模效率测度与评价、产出的超效率测度与评价及产出效率汇总评价；（3）投入产出系统效率的综合评价。

以中国商业银行经营绩效的评价工作为例，经测试，发现：该软件能够系统、准确、便捷的实现投入产出效率DEA评价相关模型的功能，能够解决系统评价中的效率评价难题，能够为相关的经济分析和管理决策提供服务。

二、需求分析

（一）应用场景

DEA在经济分析中的应用：（1）企业投入产出效率DEA评价，如评价中国各商业银行的经营绩效；（2）行业投入产出效率DEA评价，如评价房地产行业在一段时间内的运行效率；（3）市场投入产出效率DEA评价，如评价股票交易市场在一段时间内的运行效率。

DEA在管理决策中的应用：（1）生产决策，如通过DEA评价，识别出哪些生产车间有效率，哪些生产车间缺乏效率；（2）营销决策，在多个备选的市场推广方案面前，要系统性、权衡性的选出高效的市场推广方案需借助DEA方法；（3）财务决策，在成本收益分析中借助DEA方法找出开源节流的去向；（4）人事决策，在考查员工效能方面，DEA方法能够通盘考查员工数量和员工质量对工作数量和工作质量的影响；（5）研发决策，对创新绩效的DEA评价，是帮助决策者从创新投入与创新产出两个层面系统性考察各研发方案的可行性。

既然应用场景如此之多，那么DEA方法又是如何对决策单元的投入产出效率进行评价的？也就是对于软件开发而言，需要了解有关DEA评价的四个基本问题：DEA评价的原理是什么？DEA评价的模型是什么？DEA评价的内容是什么？DEA评价的标准是什么？

（二）DEA评价

1.DEA 评价数据结构

DEA模型的指标体系结构：设有m个投入指标，X1，X2，…，Xm，各投入指标依次赋非负权重v1，v2，…，vm；s个产出指标，Y1，Y2，…，Ys，各产出指标依次赋非负权重u1，u2,，…，us。在该指标体系下共有n个被评价的决策单元，DMU1，DMU2，…，DMUj，…，DMUn，如n家银行。DEA模型的数据结构：决策单元DMUj，j=1，…，n在投入维度上各指标的取值依次为X1j，X2j，…，Xmj，在产出维度上各指标的取值依次为Y1j，Y2j，…，Ysj。如此，则n个决策单元在该指标体系下构成一个 (m+s)×n的投入产出矩阵，如表1所示，其中前m×n部分为投入矩阵，后s×n部分为产出矩阵。

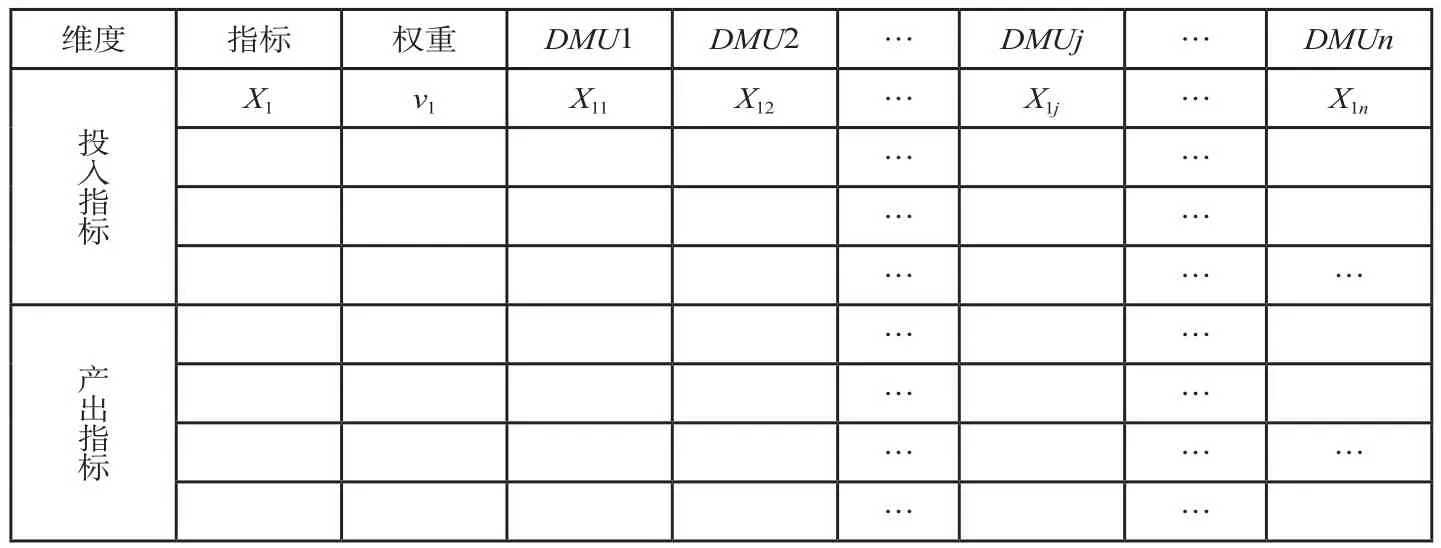
表1 投入产出效率DEA评价模型的指标体系与数据结构

2.投入效率DEA评价

对于决策单元 DMUj，j=1，…，n，找出其所处生产前沿面的数据包络分析（DEA）模型为

对（1）式的分式规划做如下Charnes-Cooper 变换

得线性规划模型为

该线性规划模型的对偶模型为

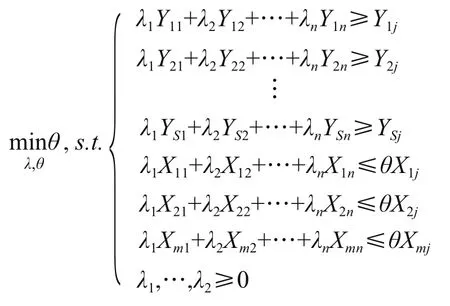
（2）式即为对决策单元 DMUj，j=1，…，n进行投入效率DEA评价的待执行模型。具体的评价标准由定理1给出。

定理1：决策单元 DMUj，j=1，…，n的投入效率DEA评价与线性规划模型（2）式的最优解θ，λ1，…，λn之间的关系为

（1）决策单元 DMUj的投入效率DEA评价为无效的充要条件是θ＜1；

（2）决策单元 DMUj的投入效率DEA评价为有效的充要条件是θ=1，且在最优解下所有不等式约束实则为等式约束；

（3）决策单元 DMUj的投入效率DEA评价为弱有效的充要条件是θ=1，且在最优解下仍有部分不等式约束严格成立。

3.产出效率DEA评价

对于决策单元 DMUj，j=1，…，n，找出其所处生产前沿面的DEA模型还可以写成

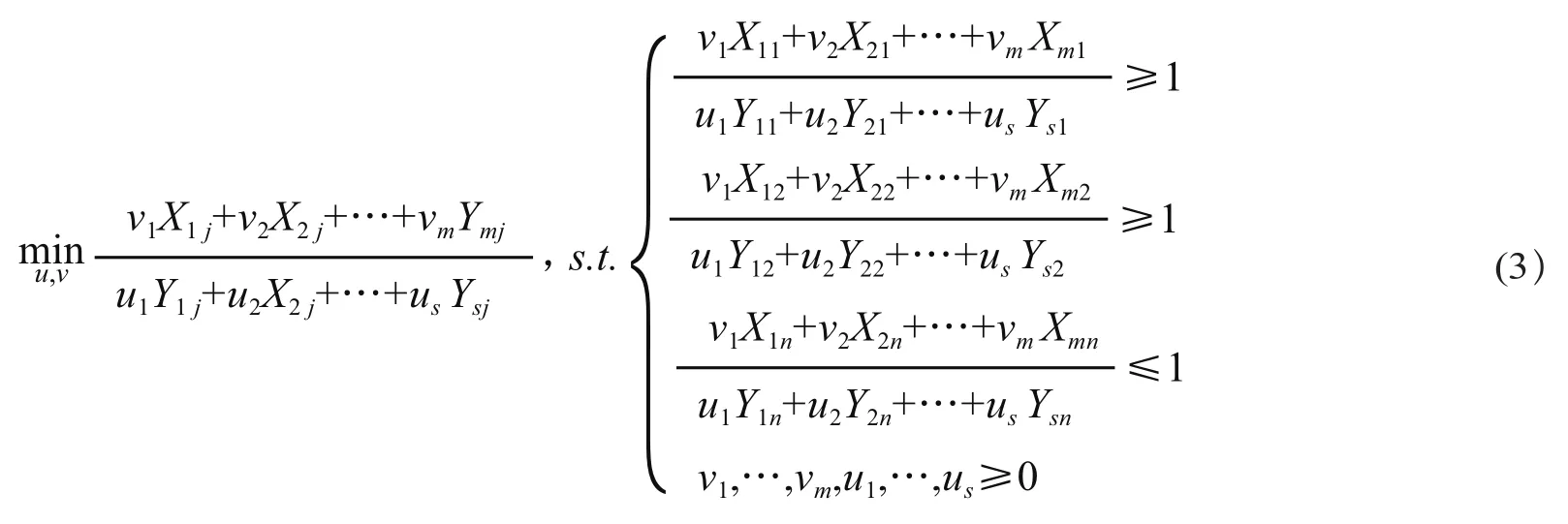
对（3）式的分式规划做如下Charness-Cooper 变换

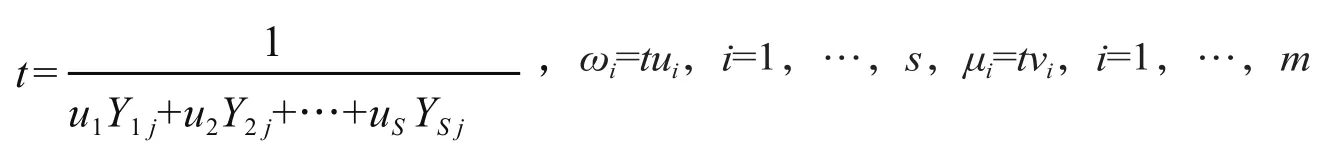
得线性规划模型为

该线性规划模型的对偶模型为

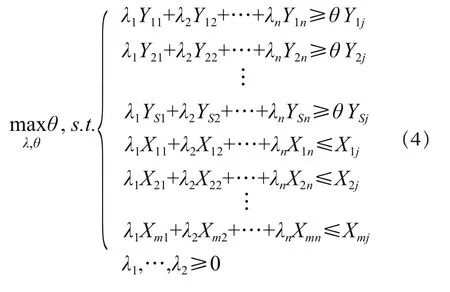
（4）式即为对决策单元DMUj，j=1，…，n进行产出效率DEA评价的待执行模型。具体的评价标准由定理2给出。

定理2：决策单元 DMUj，j=1，…，n的产出效率DEA评价与线性规划模型（4）式的最优解θ，λ1，…，λn之间的关系为

（1）决策单元 DMUj的产出效率DEA评价为无效的充要条件是θ＞1；

（2）决策单元DMUj的产出效率DEA评价为有效的充要条件是θ=1，且在最优解下所有不等式约束实则为等式约束；

（3）决策单元 DMUj的产出效率DEA评价为弱有效的充要条件是θ=1，且在最优解下仍有部分不等式约束严格成立。

由上述分析知，DEA评价的原理是：对于被评价决策单元，先找出其所处的生产前沿面，然后考察自身与其生产前沿面的距离。DEA评价的模型是：将原本是分式规划DEA模型变换为基本可执行的线性规划DEA模型，可分为投入的DEA模型（2）式和产出的DEA模型（4）式。DEA评价的内容是：投入导向的效率评价，给定产出不低于某一水平的条件下，投入越少则说明效率越高；产出导向的效率评价，给定投入不超出某一水平的条件下，产出越多则说明效率越高。DEA评价的标准是：投入效率DEA评价的基本标准如定理1所述，产出效率DEA评价的基本标准如定理2所述。接下来报告如何在MATLAB平台上开发一款基于DEA的投入产出效率评价系统，并使软件能够系统、准确、便捷的实现投入产出效率DEA评价的需求和功能。

三、系统设计

（一）系统架构

1.模块架构

如图1所示，系统共有10个功能模块组成，从数据到应用，将各模块的层级划分为底层（模块1个）、中下层（模块6个）、中上层（模块2个）、顶层（模块1个）共4个层级。（1）底层：模块1，实现结构化数据导入，形成投入产出矩阵。（2）顶层：模块4，实现投入产出系统效率DEA综评。（3）中上层：模块3.1，实现投入效率DEA汇评；模块3.2，实现产出效率DEA汇评。（4）中下层：模块2.1.1，实现投入的综合效率DEA测评；模块2.1.2，实现投入的技术效率DEA测评；模块2.1.3，实现投入的超效率DEA测评；模块2.2.1，实现产出的综合效率DEA测评；模块2.2.2，实现产出的技术效率DEA测评；模块2.2.3，实现产出的超效率DEA测评。根据图1所示模块间的链接关系知：（1）只有在底层模块功能实现后，中层和顶层的9个模块功能才能实现；（2）中层和顶层的9个功能模块既可依次实现，也可独立实现，还可跳跃实现。

2.系统主界面

系统主界面如图2所示，它是对图1所示系统模块架构的总体实现。系统分为3个顺序工作步骤：“步骤1：数据”“步骤2：分析”“步骤3：报告”。“步骤1：数据”框内的按钮“导入Excel数据”实现模块1的功能，即导入结构化数据，形成投入产出矩阵。“步骤2：分析”框内包括两个平行的子系统：投入效率DEA评价和产出效率DEA评价。在投入效率DEA评价子系统内部，按钮“综合效率DEA测评”“技术效率DEA测评”“超效率DEA测评”“投入效率DEA汇评”分别实现图1架构有关投入效率模块2.1.1、模块2.1.2、模块2.1.2和模块3.1的功能。在产出效率DEA评价子系统内部，按钮“综合效率DEA测评”“技术效率DEA测评”“超效率DEA测评”“产出效率DEA汇评”分别实现图1架构有关产出效率模块2.2.1、模块2.2.2、模块2.2.3、模块3.2的功能。“步骤3：报告”模块内的按钮“投入产出效率综评”实现图1架构有关投入产出效率模块4的功能。“步骤1：数据”与“步骤2：分析”“步骤3：报告”是串联关系，“步骤2：分析”与“步骤3：报告”以及“步骤2：分析”内部各按钮之间都是并联关系。

（二）输入输出

1.输入设计

图1 系统的功能模块及其结构

图2 系统主界面

图3 数据输入的Excel格式

在数据导入系统之前，须事先在Excel上对数据做结构化处理。以商业银行的绩效评价为例，新建一个Excel，在其Sheet1里面对原始数据进行结构化，如图3所示。操作要点如下：（1）决策单元定位，从单元格A3开始往下，依次录入各决策单元的名称。（2）指标定位，从单元格B2开始往右，依次录入所有指标的名称。先录入所有的投入指标名，然后再录入所有的产出指标名；或者先录入所有的产出指标名，然后再录入所有的投入指标名；投入指标名和产出指标名不可交替录入。（3）指标归属定位，将所有投入指标名上一行所在单元格合并，且输入“投入”二字，将所有产出指标名上一行所在单元格合并，且输入“产出”二字。或者在所有投入指标名上一行的单元格输入“投入”二字，在所有产出指标名上一行的单元格输入“产出”二字。操作完毕之后，从B1单元格往右，有且仅有“投入”“产出”两个词，而且这两个词不会交替出现。（3）数值定位，从B3单元格开始，往下是各决策单元在某个具体指标上的取值，往右是某个决策单元在各指标上的取值。从B3开始的各单元格必须是数值型数据。

2.输出设计

如图1主界面所示，系统只有1个输入，10个输出。（1）底层：输出1，报告模块1的计算结果，即输出表1指定数据结构的投入产出矩阵。将图3所示的商业银行绩效评价的Excel结构化原数据导入后，输出如图4所示的投入产出矩阵。（2）顶层：输出4，报告模块4的计算结果，即各决策单元其投入产出效率概况。界面中，表格的行名为投入指标和产出指标，表格的列名为决策单元名，表格的内容为列维度上各决策单元在行维度上对应指标的取值。（3）中上层：输出3.1，报告模块3.1的计算结果，即各决策单元其投入效率概况；输出3.2，报告模块3.2的计算结果，即各决策单元其产出效率概况。（4）中下层：输出2.1.1，报告模块2.1.1的计算结果，即各决策单元其投入的综合效率情况；输出2.1.2，报告模块2.1.2的计算结果，即各决策单元其投入的技术效率情况；输出2.1.3，报告模块2.1.3的计算结果，即各决策单元其投入的超效率情况；输出2.2.1，报告模块2.2.1的计算结果，即各决策单元其产出的综合效率情况；输出2.2.2，报告模块2.2.2的计算结果，即各决策单元其产出的技术效率情况；输出2.2.3，报告模块2.2.3的计算结果，即各决策单元其产出的超效率情况。中上层、中下层和顶层各输出设计将在对应模块的实现部分具体说明。只有点击按钮“导入Excel数据”得到输出1，即得到图4所示投入产出矩阵界面后，点击主界面上的其他按钮从有效；否则会提示先导入数据。

四、投入效率DEA汇评模块

（一）投入的综合效率DEA测评模块

1.CCR 模型

考虑到计算机的计算精度，令无穷小量ε1=10-7，ε2=10-5，将线性规划（2）式的待执行CCR模型修改为可执行CCR模型：

图4 数据输出界面

（5）式实际上是对决策单元 DMUj，j=1，…，n进行投入的综合效率DEA评价的可执行模型。具体的评价标准由定理3给出。

定理3：决策单元DMUj，j=1，…，n其投入的综合效率DEA评价与线性规划模型（5）式的最优解θ，之间的关系为

（1）决策单元 DMUj其投入的综合效率DEA评价为无效的充要条件是θ＜1；

（2）决策单元 DMUj其投入的综合效率DEA评价为有效的充要条件是θ=1，且在最优解下所有松弛变量皆不起作用，即

（3）决策单元 DMUj其投入的综合效率DEA评价为弱有效的充要条件是θ=1，且在最优解下仍有部分松弛变量在起作用，即存在某些

推论 1：由向量 (λ1，…，λn) 构成的被评价点 (Xi X j，XiY j|iX=1，…，m，iY=1，…，m) 其所处的生产前沿面 (∑j=1λj XiX j，∑j=1λj Xi Yj|iX=1，…，m，iY=1，…，m) 知，决策单元 DMUj，j=1，…，n的规模报酬值R和各投入维度的帕累托改进值 ΔXi j分别为

依此判断该决策单元 DMUj的规模报酬性质和建议投入的优化力度为

（1）决策单元 DMUj其投入的规模报酬DEA评价标准：若R=1，则决策单元DMUj其投入的规模报酬不变；若R＞1，则决策单元 DMUj其投入的规模报酬递减；若R＜1，则决策单元 DMUj其投入的规模报酬递增。

（2）若决策单元DMUj其投入的综合效率DEA评价为无效，则可按照上述帕累托改进值 ΔXij，i=1，…，m的力度来减少在相应维度的投入量。

2.程序实现

由线性规划的最优解zj得与（6）式对应的决策单元 DMUj，j=1，j=1,…，n其投入的技术效率值θ ST及向量分别为

对于标量θj和向量按照定理 4 给出的定性标准，即可判断决策单元 DMUj，j=1,…，n其投入的技术效率DEA评价为有效、弱有效抑或无效。进而，按照推论2给出的定性标准，可判断该决策单元 DMUj其投入的规模报酬DEA评价为不变、递增抑或递减；以及建议该决策单元在投入上的帕累托改进空间。

3.报表显示

点击如图1所示系统主界面投入效率DEA评价框内的“综合效率DEA测评”按钮，弹出如图5所示，投入的综合效率DEA评价结果界面。界面中，表格的列名为决策单元的名称；表格的行名称包括4个部分，①定理3所要解决的综合效率定性判断，②推论1所要解决的规模报酬定性判断，③求解线性规划模型（5）式得出的各变量θ，δX，δY，λ，④推论1中需要求解的规模报酬值和帕累托改进值两类变量；表格的内容为列维度上各决策单元在行维度上对应指标的取值。

（二）投入的技术效率DEA测评模块

1.BCC 模型

在线性规划模型（5）式中加进规模报酬不变的约束条件，则可得到对决策单元 DMUj，j=1，j=1,…，n进行投入的技术效率DEA评价模型，即如下的BCC模型：

具体的评价标准由定理4给出。

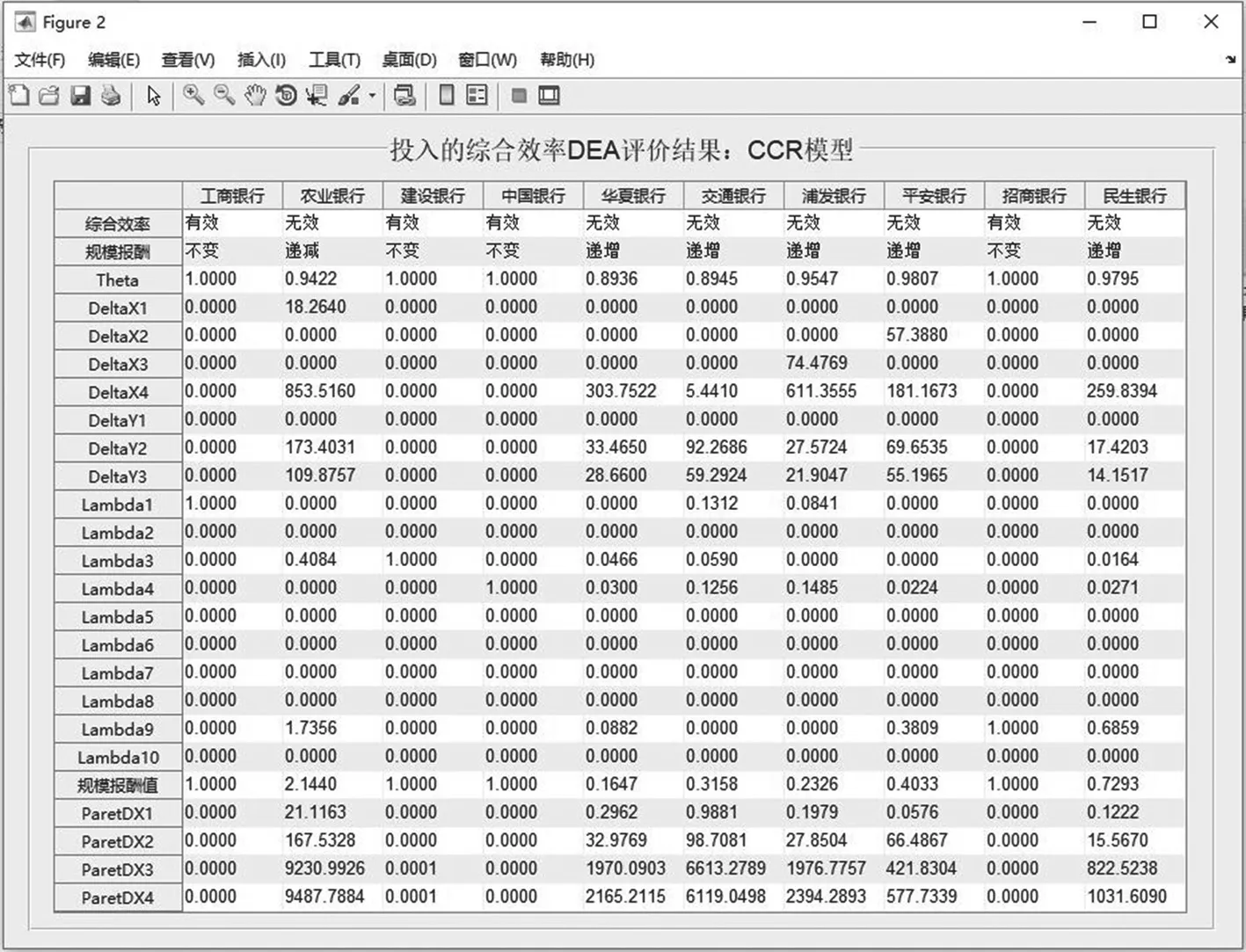
图5 投入的综合效率DEA评价结果界面

定理 4：决策单元 DMUj，j=1，…，n其投入的技术效率DEA评价与线性规划模型（6）式的最优解θ，之间的关系为

（1）决策单元DMUj其投入的技术效率DEA评价为无效的充要条件是θ＜1；

（2）决策单元DMUj其投入的技术效率DEA评价为有效的充要条件是θ=1，且在最优解下所有松弛变量皆不起作用，即

（3）决策单元 DMUj其投入的技术效率DEA评价为弱有效的充要条件是 θ=1，且在最优解下仍有部分松弛变量在起作用，即存在某些

推论 2：由（5）式计算出决策单元 DMUj，j=1，…，n其投入的综合效率值，即规模技术效率值和由（6）式计算出该决策单元其投入的技术效率值得该决策单元其投入的规模效率值以此对决策单元 DMUj，j=1，…，n进行投入的规模效率DEA评价：若则该决策单元 DMUj其投入的规模效率DEA评价为有效；否则DEA评价为无效。

2.程序实现

由线性规划的最优解zj得与（6）式对应的决策单元 DMUj，j=1，…，n其投入的技术效率值及向量分别为

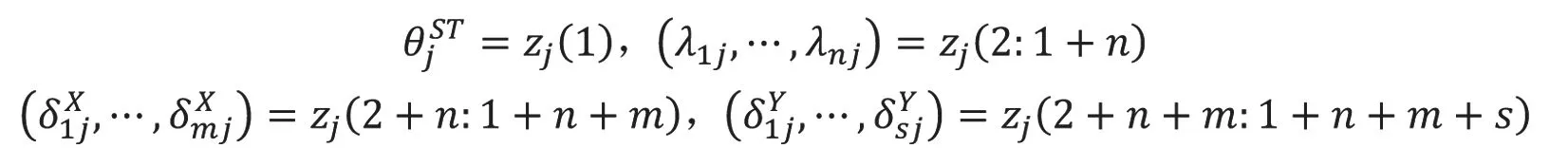
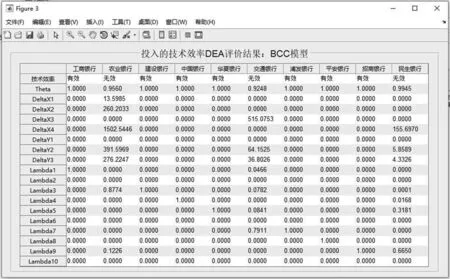
图6 投入的技术效率DEA评价结果界面

3.报表显示

点击如图1所示系统主界面投入效率DEA评价框内的“技术效率DEA测评”按钮，弹出如图6所示，投入的技术效率DEA评价结果界面。界面中，表格的列名为决策单元的名称；表格的行名称包括2个部分，①定理4所要解决的技术效率定性判断，②求解线性规划模型（6）式得出的各变量θ，δX，δY，λ；表格的内容为列维度上各决策单元在行维度上对应指标的取值。

(三) 投入的超效率DEA测评模块

1.超效率模型

要评价决策单元 DMUj，j=1，…，n的投入效率，若生产前沿面是由除DMUj自身之外的n-1 个决策单元 DMU1，…，DMUj-1，DMUj-1，…，DMUn构成，即线性规划模型变为

则被评价的决策单元 DMUj可能处于生产前沿面上，也可能处于生产前沿面之内，还可能处于生产前沿面之外。这种投入效率的DEA评价模式称为超效率评价，具体评价标准由定理5给出。

定理5：决策单元DMUj，j=1，…，n其投入的超效率DEA评价与线性规划模型（7）式的最优解θ，之间的关系为

（1）决策单元 DMUj其投入的超效率DEA评价为无效的充要条件是θ＜1；

（2）决策单元 DMUj其投入的超效率DEA评价为有效的充要条件是θ≥1，且在最优解下所有松弛变量皆不起作用，即

（3）决策单元 DMUj其投入的超效率DEA评价为弱有效的充要条件是θ≥1，且在最优解下仍有部分松弛变量在起作用，即存在某些

2.程序实现

当j=1 时，等式约束的系数矩阵Bj取值为

当 1＜j＜n时，等式约束的系数矩阵Bj取值为

当j=n时，等式约束的系数矩阵Bj取值为

由线性规划的最优解zj得与（7）式相对应的策单元 DMUj，j=1，…，n其投入的超效率值θj及向量分别为当j=1 时，(λ1j,λ2j，…，λnj)=[NaN,zj(2：n)]；当 1＜j＜n时，(λ1j，…，λj-1,j，λj,j，λj+1，j，…，λnj)=[zj(2：j)，NaN，zj(j+1：n)]；当j=n时，(λ1j，…，λn-1,j,λnj)=[zj(2：n),NaN]。对于标量θ_j 和向量按照定理 5 给出的定性标准，即可判断决策单元 DMUj，j=1，…，n其投入的超效率DEA评价为有效、弱有效抑或无效。

3.报表显示

点击如图1所示系统主界面投入效率DEA评价框内的“超效率DEA测评”按钮，弹出如图7所示，投入的超效率DEA评价结果界面。界面中，表格的列名为决策单元的名称；表格的行名称包括3个部分，①定理5所要解决的超效率定性判断，②根据投入的超效率模型（7）式计算得的效率值θ，在各决策单元之间展开投入效率排名，③求解线性规划模型（7）式得出的各变量θ,δX,δY,λ；表格的内容为列维度上各决策单元在行维度上对应指标的取值。

图7 投入的超效率DEA评价结果界面

五、产出效率DEA汇评模块

(一）产出的综合效率DEA测评模块

1.CCR 模型

考虑到计算机的计算精度，令无穷小量ε1=10-7，ε2=10-5，将线性规划（4）式的待执行CCR模型修改为可执行CCR模型：

（8）式实际上是对决策单元 DMUj，j=1，…，n进行产出的综合效率DEA评价的可执行模型。具体的评价标准由定理6给出。

定理 6：决策单元 DMUj，j=1，…，n其产出的综合效率 DEA 评价与线性规划模型（8）式的最优解θ，之间的关系为

（1）决策单元 DMUj其产出的综合效率DEA评价为无效的充要条件是θ＞1；

（2）决策单元 DMUj其产出的综合效率DEA评价为有效的充要条件是θ=1，且在最优解下所有松弛变量皆不起作用，即

（3）决策单元 DMUj其产出的综合效率DEA评价为弱有效的充要条件是θ=1，且在最优解下仍有部分松弛变量在起作用，即存在某些

推论 3：由向量 (λ1，…，λn) 构成的被评价点 (XiX j，XiY j) |iX=1，…，m,iY=1，…，m) 其所处的生产前沿面 (∑j=1λj知，决策单元 DMUj，j=1，…，n的规模报酬值R和各产出维度的帕累托改进值 ΔYij分别为

依次判断该决策单元 DMUj的规模报酬性质和建议产出的优化力度为

（1）决策单元 DMUj其产出的规模报酬DEA评价标准：若R=1，则决策单元 DMUj其产出的规模报酬不变；若R＞1，则决策单元 DMUj其产出的规模报酬递减；若R＜1，则决策单元DMUj其产出的规模报酬递增。

（2）若决策单元 DMUj其产出的综合效率DEA评价为无效，则可按照上述帕累托改进值 ΔYij，i=1，…，m的力度来增加在相应维度的产出量。

2.程序实现

由线性规划的最优解zj得与（8）式对应的决策单元 DMUj，j=1，…，n其产出的综合效率值及向量分别为

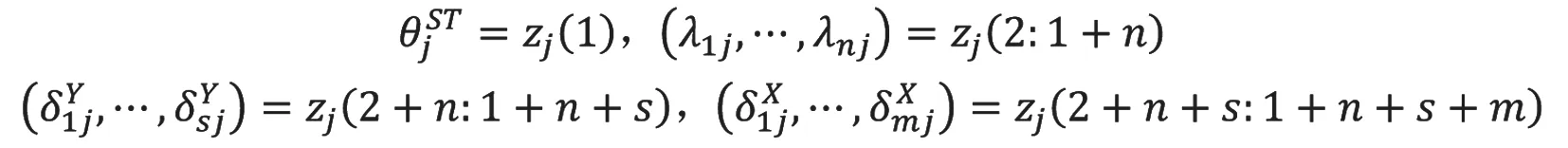
图8 产出的综合效率DEA评价结果界面

3.报表显示

点击如图1所示系统主界面产出效率DEA评价框内的“综合效率DEA测评”按钮，弹出如图8所示，产出的综合效率DEA评价结果界面。界面中，表格的列名为决策单元的名称；表格的行名称包括4个部分，①定理6所要解决的综合效率定性判断，②推论3所要解决的规模报酬定性判断，③求解线性规划模型（8）式得出的各变量θ，δX，δY，λ，④推论3中需要求解的规模报酬值和帕累托改进值两类变量；表格的内容为列维度上各决策单元在行维度上对应指标的取值。

（二）产出的技术效率DEA测评模块

1.BCC 模型

在线性规划模型（8）式中加进规模报酬不变的约束条件，则可得到对决策单元DMUj，j=1，…，n进行产出的技术效率DEA评价模型，即如下的BCC模型：

具体的评价标准由定理7给出。

定理7：决策单元DMUj其产出的技术效率DEA评价与线性规划模型（9）式的最优解θ，λ1，…，之间的关系为

（1）决策单元DMUj其产出的技术效率DEA评价为无效的充要条件是θ＞1；

（2）决策单元 DMUj其产出的技术效率DEA评价为有效的充要条件是θ=1，且在最优解下所有松弛变量皆不起作用，即

（3）决策单元DMUj其产出的技术效率DEA评价为弱有效的充要条件是θ=1，且在最优解下仍有部分松弛变量在起作用，即存在某些

推论 4：由（8）式计算出决策单元 DMUj，j=1，…，n其产出的综合效率值，即规模技术效率值和由（9）式计算出该决策单元其产出的技术效率值得该决策单元其产出的规模效率值以此对决策单元 DMUj，j=1，…，n进行产出的规模效率 DEA 评价 ：若则该决策单元 DMUj其产出的规模效率DEA评价为有效；否则DEA评价为无效。

2.程序实现

由线性规划的最优解zj得与（9）式对应的决策单元 DMUj，j=1，…，n其产出的技术效率值及向量分别为

3.报表显示

点击如图1所示系统主界面产出效率DEA评价框内的“技术效率DEA测评”按钮，弹出如图9所示，产出的技术效率DEA评价结果界面。界面中，表格的列名为决策单元的名称；表格的行名称包括2个部分，①定理4所要解决的技术效率定性判断，②求解线性规划模型（9）式得出的各变量θ,δX,δY,λ；表格的内容为列维度上各决策单元在行维度上对应指标的取值。

（三）产出的超效率DEA测评模块

1.超效率模型

要评价决策单元DMUj，j=1，…，n的产出效率，若生产前沿面是由除 DMUj自身之外的n-1 个决策单元 DMU1，…，DMUj-1，DMUj+1，…，DMUn构成，即线性规划模型变为

则被评价的决策单元 DMUj可能处于生产前沿面上，也可能处于生产前沿面之内，还可能处于生产前沿面之外。这种产出效率的DEA评价模式称为超效率评价，具体评价标准由定理8给出。

定理 8 ：决策单元 DMUj其产出的超效率 DEA 评价与线性规划模型（10）式的最优解θ,λ1,…,λn,之间的关系为

（1）决策单元 DMUj其产出的超效率DEA评价为无效的充要条件是θ＞1；

（2）决策单元 DMUj其产出的超效率DEA评价为有效的充要条件是θ≤1，且在最优解下所有松弛变量皆不起作用，即

（3）决策单元DMUj其产出的超效率DEA评价为弱有效的充要条件是θ≤1，且在最优解下仍有部分松弛变量在起作用，即存在某些

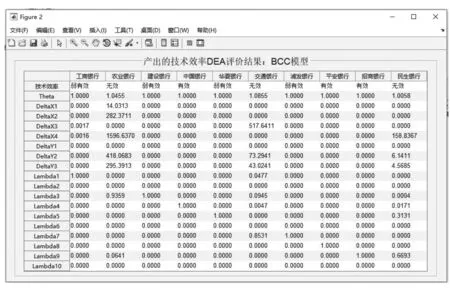
图9 产出的技术效率DEA评价结果界面

2.程序实现

当j=1 时，等式约束的系数矩阵Bj取值为

当 1＜j＜n时，等式约束的系数矩阵Bj取值为

当j=n时，等式约束的系数矩阵Bj取值为

由线性规划的最优解zj得与（10）式相对应的策单元 DMUj，j=1，…，n其产出的超效率值θj及向量分别为当j=1 时，(λ1j,λ2j,…,λnj)=[NaN,zj(2：n)]；当 1＜j＜n时，(λ1j,…,λj-1,j),λj,j,λj+1,j,…,λnj)=[zj(2：j),NaN,zj(j+1：n)]；当j=n时，(λ1j, …,λn-1,j,λnj)=[zj(2：n),NaN]。对于标量θj和向量按照定理 8 给出的定性标准，即可判断决策单元 DMUj，j=1，…，n其产出的超效率DEA评价为有效、弱有效抑或无效。

3.报表显示

点击如图1所示系统主界面产出效率DEA评价框内的“超效率DEA测评”按钮，弹出如图10所示，产出的超效率DEA评价结果界面。界面中，表格的列名为决策单元的名称；表格的行名称包括3个部分，①定理8所要解决的超效率定性判断，②根据产出的超效率模型（10）式计算得的效率值 θ，在各决策单元之间展开产出效率排名，③求解线性规划模型（10）式得出的各变量 θ,δ^X,δ^Y,λ；表格的内容为列维度上各决策单元在行维度上对应指标的取值。

六、系统测试

（一）投入效率DEA汇评

图5至图7分别测试完投入的综合效率、技术效率、超效率三个模块的DEA测评结果，下面测试投入效率DEA汇评结果。在如图1所示系统主界面的投入效率DEA评价框内，点击按钮“投入效率DEA汇评”，弹出如图11所示各决策单元其投入效率DEA评价结果的汇总界面。界面中，表格的行名为决策单元的名称；表格的列名称包括3个部分，①投入的综合效率值、技术效率值、规模效率值、超效率值共4个定量指标，②投入的综合效率、技术效率、规模效率、超效率共4个定性指标，③根据超效率值而来的投入效率排名；表格的内容为行维度上各决策单元在列维度上对应指标的取值。其中规模效率值是由推论2的规模效率公式计算得来，规模效率定性判断是根据推论2的判断标准得出的。

（二）产出效率DEA汇评

图8至图9分别测试完产出的综合效率、技术效率、超效率三个模块的DEA测评结果，下面测试产出效率DEA汇评结果。在如图1所示系统主界面的投入效率DEA评价框内，点击按钮“投入效率DEA汇评”，弹出如图12所示各决策单元其投入效率DEA评价结果的汇总界面。界面中，表格的行名为决策单元的名称；表格的列名称包括3个部分，①产出的综合效率值、技术效率值、规模效率值、超效率值共4个定量指标，②产出的综合效率、技术效率、规模效率、超效率共4个定性指标，③根据超效率值而来的产出效率排名；表格的内容为行维度上各决策单元在列维度上对应指标的取值。其中规模效率值是由推论4的规模效率公式计算得来，规模效率定性判断是根据推论4的判断标准得出的。

（三）投入产出系统效率DEA综评

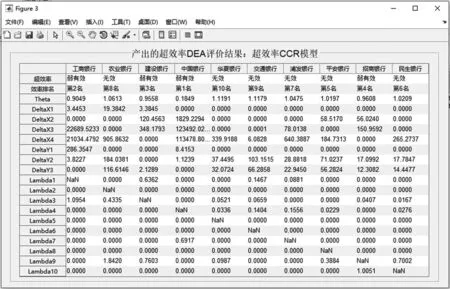
图10 产出的超效率DEA评价结果界面

图11 投入效率DEA评价结果汇总界面

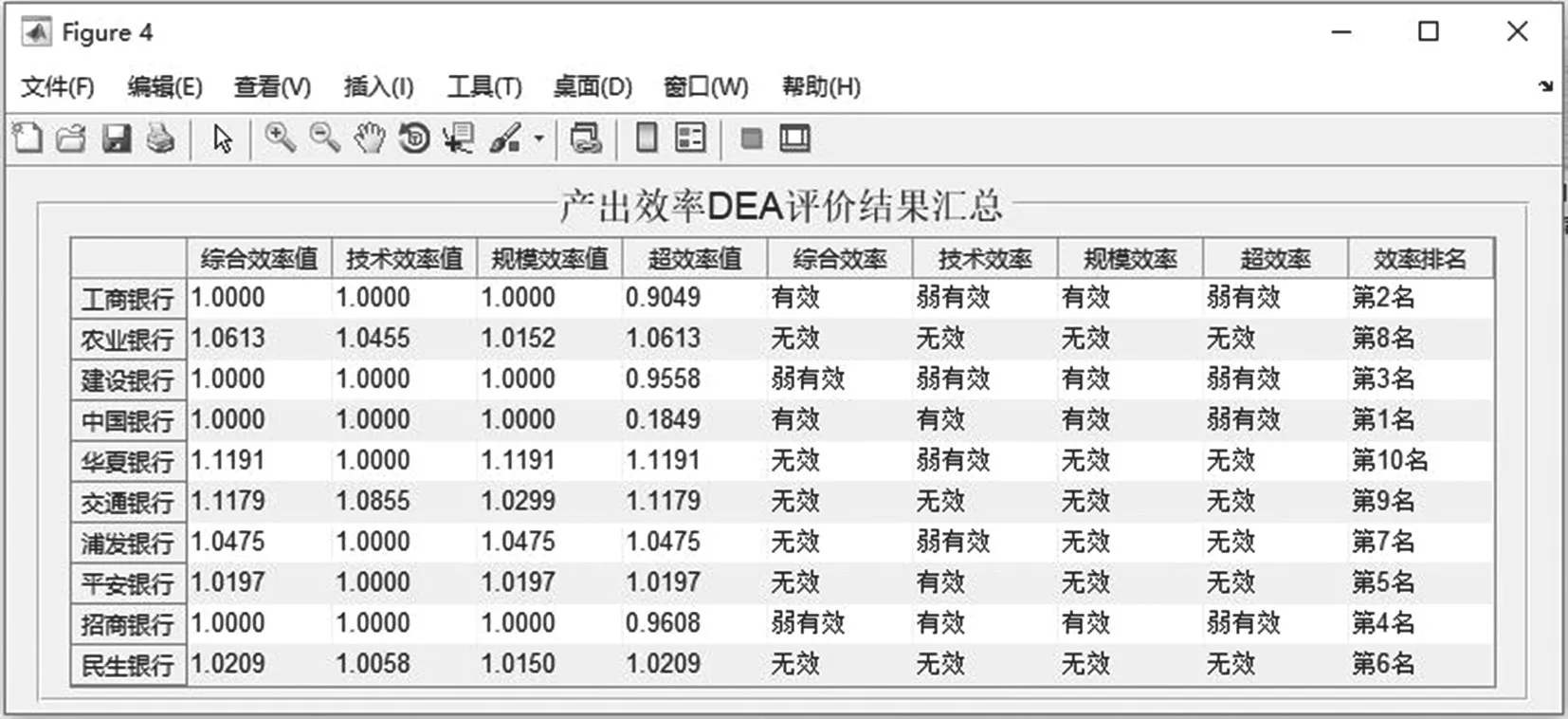
图12 产出效率DEA评价结果汇总界面

图13 投入产出效率DEA评价结果汇总界面

在如图1所示系统主界面的“步骤3：报告”框内，点击按钮“投入产出效率综评”，弹出如图13所示各决策单元其投入产出效率DEA评价结果的汇总界面。界面中，表格的行名为决策单元的名称；表格的列名称包括3个部分，①投入产出效率的定性判断，②投入产出的效率排名，③投入效率值、产出效率值、投入效率指数、产出效率指数共4个定量指标；表格的内容为行维度上各决策单元在列维度上对应指标的取值。其中投入产出效率定性判断的标准是：对于被评价的某个决策单元，只有其投入效率值和产出效率值皆为1，即投入和产出都为DEA有效（含弱有效）时，才能认定该决策单元其投入产出效率评价为“有效”，否则评价为“无效”。各决策单元的投入效率指数和产出效率指数分别为图11对应决策单元其投入的超效率值和图12对应决策单元其产出的综合效率值。投入产出的效率排名是图11所示投入效率排名和图12所示产出效率排名的综合排名：一般而言，投入效率排名与产出效率排名是一致的；倘若出现个别差异，会同时将投入效率排名位次和产出效率排名位次在同一个单元格里报告出来。

七、结束语

对于经济分析和管理决策中的系统评价问题，在MATLAB平台上开发出一款基于DEA的投入产出效率评价系统。系统的功能主要有：（1）投入效率评价，具体包括投入的综合效率测度与评价、投入的技术效率测度与评价、投入的规模效率测度与评价、投入的超效率测度与评价及投入效率汇总评价；（2）产出效率评价，具体包括产出的综合效率测度与评价、产出的技术效率测度与评价、产出的规模效率测度与评价、产出的超效率测度与评价及产出效率汇总评价；（3）投入产出系统效率的综合评价。对中国商业银行经营绩效评价做测试发现，该软件能够系统、准确、便捷的实现投入产出效率DEA评价不同模型的功能，能够解决系统评价中的效率评价难题，能够为相关的经济分析和管理决策提供服务。