混流式水轮机转轮模态计算及振动特性分析
史广泰,杨 茜,刘宗库,薛志成
(1.西华大学流体及动力机械教育部重点实验室,四川 成都 610039;2.西华大学能源与动力工程学院,四川 成都 610039)
作为一种极为重要的旋转机械,水轮机的安全可靠运行直接影响企业效益和经济发展[1]。但近年来通过分析水电站运行资料发现,水轮机转轮经常产生疲劳破坏,甚至断裂,这成为水轮机组运行及我国水电事业发展的潜在威胁,同时也成为业内人士关注的重点。多年来许多学者对此进行研究,并取得了显著的成效。刘德民等[2]采用流固耦合方法对某混流式水轮机进行振动分析,并比较了流量和离心力对转轮模态的影响。岳志伟等[3]基于ANSYS有限元计算平台利用流固耦合理论对可逆式水轮机转轮进行干、湿模态分析,结果表明转轮叶片的最大变形出现在叶片出水边中部。梁权伟等[4]利用顺序流固耦合的方法对混流式水轮机转轮进行强度和模态分析,并与实际发生疲劳位置相对比,结果表明转轮发生疲劳原因不是静应力而是动载荷。吕桂萍等[5]通过对混流式水轮机转轮固有频率进行分析,得到了水轮机发生共振的影响因素。廖伟丽等[6]运用有限元分析方法对混流式水轮机转轮以及整体进行模态分析,得到了水轮机转轮单叶片和整体固有频率,分析水轮机过流部件水力激振频率与水轮机机组共振频率之间的关系。除了上述文献外,其他一些学者也对水轮机转轮进行了相关研究,并得到了显著成果[7-11]。
水轮机在运转过程中受到自身重力、旋转惯性力和水力不稳定性的影响,其应力应变情况非常复杂,故本文针对国内某电站水轮机转轮叶片表面出现的裂纹、断裂的具体情况,在总结前人研究成果的基础上,应用流固耦合理论对水轮机转轮进行模态分析,进而总结其变形及振动特性。
1 数值计算方法
1.1 标准k-ε模型
本文采用标准的k-ε湍流模型,其方程如下:

(1)
式中:k、ε分别是湍动能和湍流耗散率;μt为湍流黏性系数;模型常数Cε1=1.44,Cε2=1.92,σε=1.3,σk=1.3。
1.2 固体弹性结构有限元理论
对转轮叶片模态分析得到的转轮叶片动应力主要是由低频组成的,因此本文在数值计算过程中,结构瞬态响应求解采用Ansys有限元提供的隐式求解法Newmark时间积分法,具体方程如下:
(2)
(3)
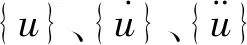
(4)
(5)
式中,ut+Δt可由t+Δt时刻的运动方程求得,即
(6)
当γ≥0.5、β≥0.25(γ+0.5)2时,Newmark法无条件稳定,即数值计算的过程中,解的稳定性不受时间步长大小的影响。
2 研究对象及模型建立
本文研究对象为混流式水轮机,其型式为:HLD307-LJ-290。基本参数为:额定出力,92.3 MW;最大出力,107 MW;最大水头,184 m;额定水头,159.3 m;额定流量,62.7 m3/s;额定转速,272.7 r/min;最大吸出高度,-3 m。
首先利用Unigraphics NX的几何建模功能,建立本水轮机的三维几何模型,如图1所示为水轮机的三维水体几何模型。
3 网格划分及边界条件设置
由于水轮机各过流部件结构复杂,而且转轮叶片为三维扭曲曲面,形状不规则,因此采用适应性较强的非结构网格对流体域及转轮实体进行网格划分,并对关注的区域网格进行局部加密。这样既能保证网格的生成速度和后续计算的准确性,也可提高计算效率。经过网格无关性验证后,最终确定的计算域网格数为500万左右,其中转轮实体的网格数为60万左右,网格划分如图2所示。
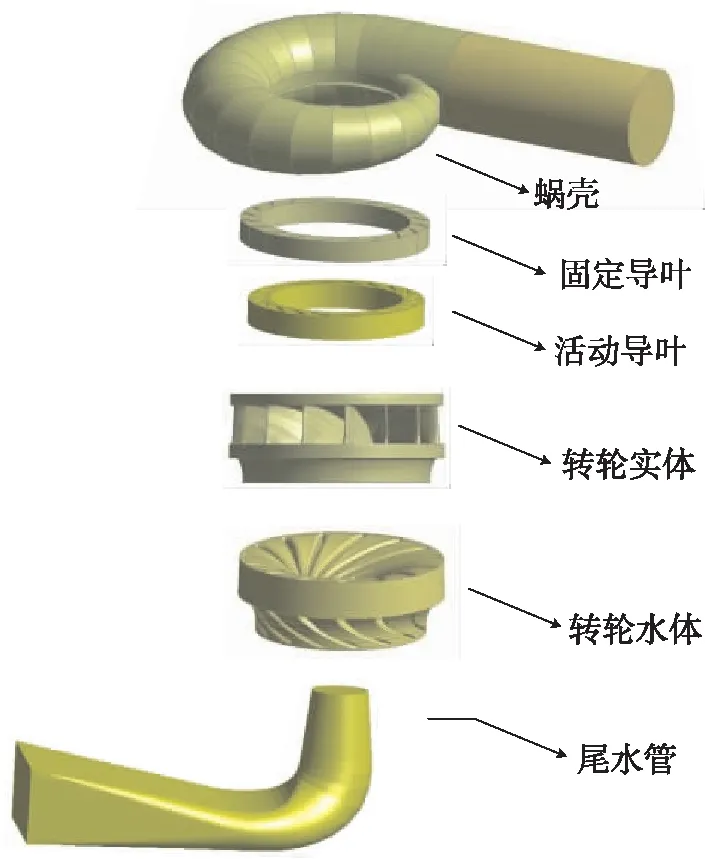
图1 水轮机三维几何模型

图2 水轮机过流部件网格划分
网格划分完成后,运用Ansys Workbench 平台对水轮机全流道进行数值模拟。其边界条件设置如下:水轮机蜗壳进口和尾水管出口分别设为总压进口和静压出口。另外,活动导叶和转轮进口交界面设置为动静交界面,壁面选用无滑移壁面,参考压力为一个大气压。
在进行流固耦合计算时,转轮上冠轴承处设置固定约束并考虑离心力的作用,并将转轮流体域受到的压力加载到转轮实体上。
4 转轮模态振动分析
4.1 固有频率分析
表1为在额定水头3种典型开度(40%、70%和100%)下转轮在水中的固有频率。

表1 不同工况下转轮在水中的固有频率
由表1可知:不同工况对应相同的阶次转轮的固有频率相差很小,因此本文后续选取100%一种工况进行模态和振动分析。
表2为在100%开度工况下转轮自由模态和预应力模态的固有频率。由表2可知:在有预应力的情况下顶盖的固有频率比自由模态情况下显著降低,各阶频率变化率均高于34%,因此预应力对转轮模态分析影响很大,在转轮的模态分析中不可忽视其影响。

表2 转轮自由模态和有预应力下的固有频率
4.2 转轮振型分析
考虑到机组的实际运行情况以及文章篇幅,本文选取额定水头100%开度工况进行后续分析。
图3为转轮自由模态的前6阶振型图。由图3可知,转轮的第1、2阶振型相似,主要表现为弯曲变形。在上冠轴孔附近变形量较小,并且最小变形区域呈对称分布,而最大变形量出现在叶片出水边靠近下环处。另外还发现下环变形量略大于上冠。
转轮的第3阶振型主要表现为绕轴旋转。从变形量分析,转轮变形量绕旋转轴对称性较好,最大变形量出现在叶片出水边靠近泄水锥处,而最小变形量则出现在叶片进水边中部,上冠变形量由轴孔向外逐渐增大。
转轮的第4、5阶振型相似,主要表现为泄水锥的左右摆动和叶片的弯曲变形。最大变形量出现在叶片出水边,最小变形量出现在叶片进水边中部。
转轮的第6阶振型主要表现为下环和叶片的局部弯曲变形。下环变形成为了三角形,上冠和下环的相对位置基本保持不变。叶片表现为非常明显的扭转。转轮上冠和泄水锥处变形较小,最大变形量仍然出现在叶片出水边。
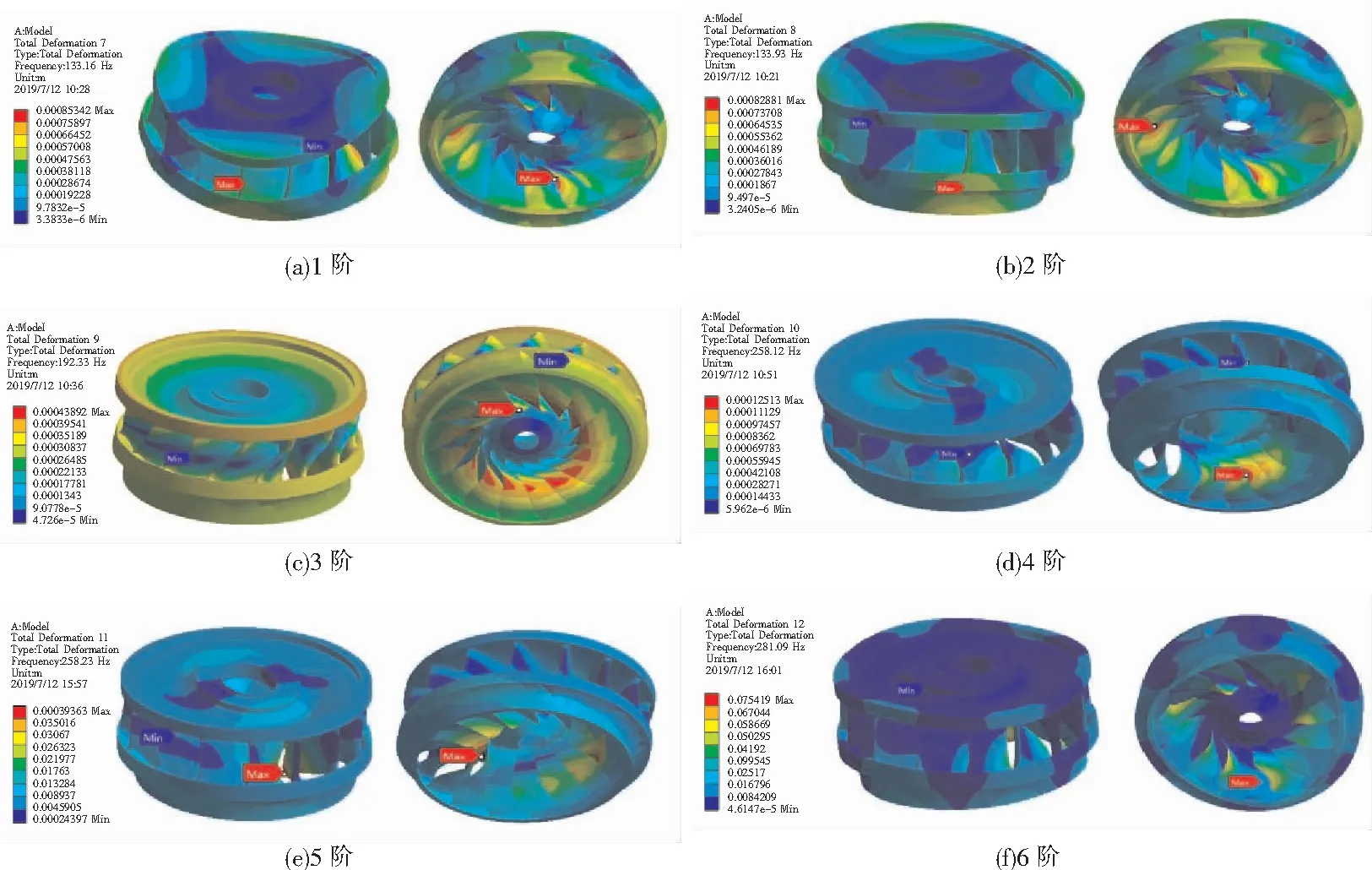
图3 水轮机转轮自由模态前6阶振型
当振动频率较低时,振动形式是以转轮的整体振动为主导,但是随着频率的不断升高,转轮的振动形式逐渐变为以局部振动为主导。
图4为水轮机转轮预应力模态下的振型图。

图4 转轮各阶固有频率对应的振型图
由图4可知,转轮第1、2阶振型主要表现为类似于钟摆的整体摆动,最大和最小变形分别出现在上冠和下环处,在叶片出水边变形量沿着泄水锥到下环方向逐渐增大。
转轮的第3阶振型主要表现为绕轴的旋转运动,转轮上冠处变形量从轴孔到外缘逐渐增加且在轴孔以及泄水锥附近变形量最小,在下环以及下环靠近叶片进水边处的形变量相对较大。另外发现叶片出水边靠近下环变形量明显较大。
转轮的第4、5阶振型主要表现为弯曲变形,其振型图相似。上冠最小变形区域和叶片出水边最大变形区域绕轴对称分布,转轮整体变形不均匀程度较大。
转轮的第6阶振型主要表现为转轮上冠沿轴向方向上下振动,转轮下环的变形量相比上冠来说较小。另外,还发现叶片出水边变形较为均匀,而在叶片进水边处变形梯度较大。
由上述分析可知水轮机转轮振动形式主要有4种,分别为摆动、绕轴旋转、弯曲变形及沿轴向方向上下振动。同时发现,频率相近的低阶振型具有一定的对称性。这主要是由于转轮结构和周围约束具有对称性所致。1阶、2阶、3阶及6阶频率下的振动以转轮的整体振动为主,而4阶及5阶频率下的振动以局部振动为主。另外,由于固定约束施加在上冠轴孔处,所以上冠形变小,同时转轮的最大变形主要集中在转轮上冠和下环以及进出水边局部位置的叶片出水边和下环处。图5为转轮实际变形位置。由图可知在叶片出水边靠近泄水锥附近产生裂纹,而在叶片出水边靠近下环处发生断裂。这是由于叶片根部应力过大所致。


图5 转轮实际发生破坏的位置
4.3 转轮振动特性分析
4.3.1 典型激振力频率的计算
1)导叶出口水流引发的脉动。
导叶出口的不均匀流动会对转轮产生一定程度的扰动,其作用于转轮上的水流扰动频率可以通过下式计算得出:
(7)
式中:n为水力机组的转速;zg为活动导叶的个数。由式(7)可以得到在计算工况下(n=272.7 r/min)的活动导叶出口水流引发的脉动频率为109.08 Hz。
2)叶片的旋转频率。
水轮机转轮叶片在旋转的过程中,水流从叶片进口到出口,作用力随转频周期性变化,其频率可按下式计算:
(8)
式中:n为水力机组的转速;z为转轮的叶片个数。利用式(8)可以得到转轮在计算工况下(n=272.7 r/min)的旋转频率为68.175 Hz。
4.3.2 转轮固有频率与典型激振力频率的对比分析
转轮的激振频率如表3所示。通过对比表2和表3中数据可以看出:水轮机在转速n=272.7 r/min下运行时,转轮的第3阶固有频率与导叶出口水流引发的脉动频率几乎相等,可能会诱发转轮共振,从而引起机组振动幅度急剧增加;而其他固有频率与激振频率相差较大,所以共振可能性较小。

表3 转轮可能的激振频率
5 结论
1)水轮机转轮振动形式主要有4种,分别为摆动、绕轴旋转、弯曲变形及沿轴向方向上下振动。同时发现预应力对转轮模态分析影响很大,在转轮的模态分析中不可忽视其影响。
2)在预应力模态分析中,第1阶和第2阶、第4阶和第5阶振型相似。另外,水轮机转轮最大变形主要位于转轮上冠、下环以及叶片出水边中部。
3)水轮机在转速n=272.7 r/min下运行时,转轮的第3阶固有频率与导叶出口水流引发的脉动的频率几乎相等,可能会诱发转轮共振。同时,发现在水轮机实际运行过程中,由于转轮叶片根部应力过大而导致叶片断裂。
——“AABC”和“无X无X”式词语

