基于海面位势高度和海表温度构建西太平洋三维温度场❋
范秀梅, 樊 伟, 杨胜龙, 周为峰, 伍玉梅
(中国水产科学研究院渔业资源遥感信息技术重点开放实验室,上海200090)
海洋卫星提供了连续、稳定和丰富的海面数据,如SST和SLA,例如,星载的中分辨率成像光谱辐射计MODIS (Moderate Resolution Imaging Spectroradiometer)每2天观测一次整个地球表面,因此它可以提供足够的SST数据[1-2]。到2018年1月,世界海洋中大约有3 890个自由漂流的Argo浮标,目前正在对从海面到2 000 m深度[3]的温盐等要素进行实时观测,但是Argo浮标在全球大洋中分布不均匀。全球海洋如此广阔,仅根据Argo剖面[4]很难获得高分辨率网格化的三维温度场。基于丰富的海表数据,海洋学家们已经做了大量的研究工作来重建水下海温数据。
Fox等[5]设计并介绍了MODAS(Modular Ocean Data Assimilation System)系统,该系统用于重构全球海洋的三维温度场和盐度场。MODAS使用《1994年世界海洋地图集》WOA’94(World Ocean Atlas 1994)T/S气候学作为背景场,通过最优插值方法OI[6](Optimal Interpolation)从海洋观测数据集( MOODS )中同化吸收历史T / S剖面,然后可以得到代表海洋平均状态的静态MOADS三维温盐场。利用历史观测记录的温度和盐度廓线求得水下的温盐值和海表温度、海面位势高度的回归方程,借助该方程和近实时的卫星观测的SST、海面高度可以计算动态MOADS三维温场。因此,它可以被用作初始的第一猜测场,通过最优插值法同化吸收任何现场数据,然后它将提供比静态MOADS气候学更准确的“真实海洋”估计。这种方法基于长期历史观测剖面数据和气候态的温盐场。
Nardelli等[7]应用m-EOF(Multivariate Empirical Orthogonal Function)方法分析了长时间序列的海水温度、盐度和海面位势高度数据,然后基于前三个EOF模态获得了线性回归方程,它把海表面的性质向水下投影。然后基于该回归方程重建了北太平洋的垂直剖面。这种方法依赖于两个假设:一个是只需要EOF分析结果的前几个模态可以解释矩阵的大部分的值;另一个是海表温度和海表位势高度、海面盐度之间存在很强的线性关系。Nardelli 等[8]和Yosuke等[9]还使用了一种类似于该m-EOF方法的方法来重构局部海域的温度剖面。这种m-EOF方法是基于长期数据的多元EOF分析,因此即使在最坏的情况下,重建温度也可以与气候态的数据接近。Guinehut等[10]使用长期的历史温度和盐度剖面以及月平均数据来获得变量间的线性回归方程,然后再基于该线性回归方程和卫星观测的海表温度,海面高度异常及月平均数据进行温度场的重构。
Alvera-Azcárate等[11]和王辉赞[12-13]使用EOF分析来恢复缺失数据,如温度和盐度,EOF分析首先分解时间序列数据组成的矩阵,然后选择主成分来计算缺失数据。这种方法要求在该矩阵中缺失的数据点附近必须存在观测值,即只是少量的数据缺失,否则结果将偏离真实值。
本文通过以下方式改进了上述重构三维海洋温度场的方法。首先,作者没有应用多年观测,而是使用了前一年来自CMEMS的3-D月平均温盐场,这是根据Guinehut的方法重建的。使用下一年的卫星观测的月平均海表数据 (SLA和SST)来推导下一年的3-D月平均温度场。使用相邻或相近年份的数据集来获得海表和水下要素之间的线性回归关系可以提高重建的准确性,因为两个数据集越近,它们之间的相关性就越高,均方根差异越小。其次还利用最有插值方法同化吸收了Argo的实测数据以提高精度。
2 数据
总共需要三种数据:三维T/S场用于设定水下温度和海表温度、海表位势高度的回归关系;SST和SLA等海表的遥感数据用于重建三维温度场;用Argo剖面数据同化以提高结果的准确性。
2.1 三维温度和盐度场
三维温度和盐度场是CMEMS提供的MULTIOBS_GLO_PHY_REP_015_002月平均数据集,下载地址http://marine.copernicus.eu/services-portfolio/access-to-products/。空间分辨率为1/4(°),垂直范围从- 5 500~0 m分成33个等级;时间覆盖范围是从1993—2016年。这个数据集是使用第1节引言中提到的Guinehut方法构建的。
多年平均海温和盐度数据来自NOAA(National Oceanic and Atmospheric Administration)提供的WOA2018(World Ocean Atlas 2018)数据集。温盐数据为多年平均(2005—2017年)的各月的三维数据,空间分辨率为1/4(°),下载地址https://www.nodc.noaa.gov/OC5/woa18/woa18data.html。
2.2 遥感数据集
SST由NASA的海洋水色网提供,下载地址https://oceandata.sci.gsfc.nasa.gov/,该数据通过负载在Terra卫星和Aqua卫星上的MODIS观测的。Modis-Aqua下午从南向北穿越赤道,而Modis-Terra则是早上从北向南穿越赤道。本文分别从两颗卫星下载月平均9 km的SST,然后将它们合并在一起。
平均动力地形MDT(Mean Dynamic Topography)是指参考大地水准面的平均海面高度。MDT_CNET-CLS13是AVISO发布的1993—2012年期间海洋MDT的估计,相应的网格分辨率为1/4(°),如图1(a)所示。下载地址https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/mdt.html。
SLA (海平面异常)是海面高度减去长时间序列的平均海面高度所得的值,平均海面高度由地球重力、海洋环流等决定。文中使用了CMEMS提供的CLS-DOS-NT-06-034的月平均SLA,这是延迟时间为4个月的相对于1999—2012年的平均海面高度的海面高度异常,海面高度素来自全球海洋很多的卫星观测。它是分辨率为1/4(°)的网格产品, 2014年6月的海面高度异常如图1(b)所示。
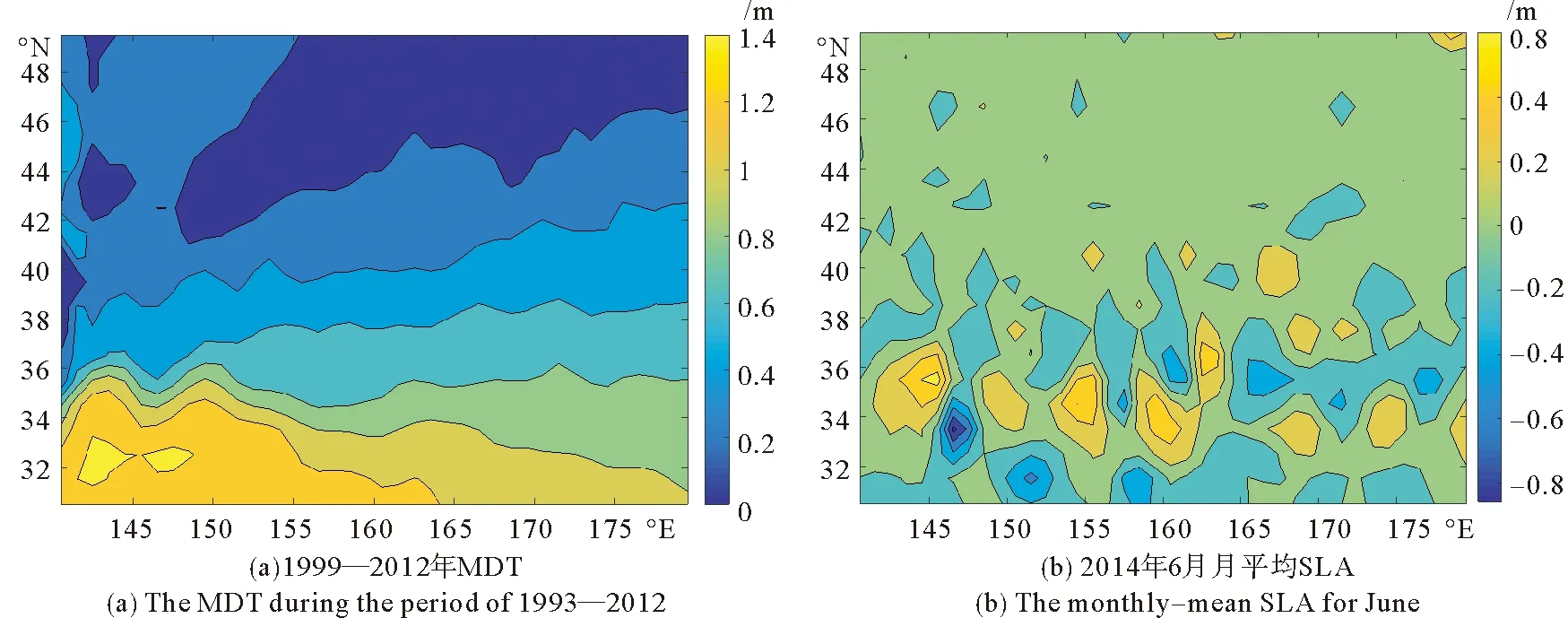
图1 平均动力地形和月平均海面高度异常Fig.1 Mean dynamic topography and mothly-mean sea level anomalies
2.3 Argo剖面数据
Argo是科学家们于1999年开始布置的全球海洋范围的温度/盐度剖面观测浮标。下载的Argo剖面数据需要剔除不合格的数据,例如具有压力梯度的异常等。计算的深度是1 000 m,所以选择剖面深度大于1 000 m,区域范围是140°W ~180°W,30°N ~ 50°N,在这个区域,2014年Argo观测的温度剖面线数量是3 512个,2015年是4 646个,2016年是4 298个(见图2)。

((a)、(b)和(c)分别代表Argo观测的2014、2015和2016年的合格温度剖面线的观测地点,不同月份对应不同的颜色。(a), (b) and (c) represent the Argo annual observational points for 2014, 2015 and 2016 separately with different colors corresponding to different months, which have been dealt with by removing the unqualified profiles.)
图2 Argo 观测位置点
Fig.2 Argo observation points
3 重构温度场的流程
重构三维温度场的过程分为2步(见图3):(1)通过多元线性回归方程得到温度场T1;(2)利用最优插值的同化方法,T1吸收同化进Argo观测的温度值,从而得到准确度更高的温度场T2。下面将更详细的说明每一步。
3.1 建立回归方程
3.1.1 求解多元线性回归方程的常系数和平均值 选取西太平洋区域作研究区域,该三维水域的水平海域范围设定为:30°N~50°N,140°W~180°W,水平分辨率为1°;深度方向为从海表至-1 000 m,划分为19层(0, 10, 20, 30, 50, 75, 100, 125, 150, 200, 250, 300, 400, 500, 600, 700, 800, 900, 1 000 m)。在每个空间网格点上建立海温和海表位势高度、海表温度的线性方程。在空间位置i,深度k,时间t处的二元一次线性方程为:

(1)

(2)

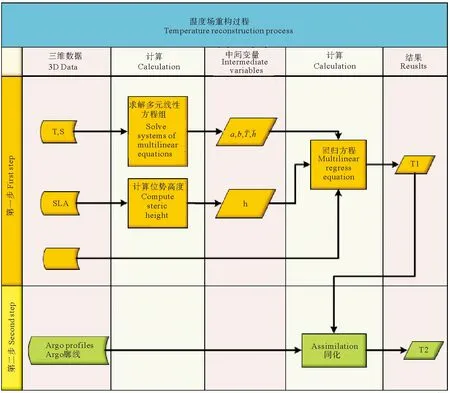
(输入T、S表示第一年的来自CMEMS的再分析温度和盐度三维数据,输入SLA和SST是第二年的卫星观测数据。输入Argo温度廓线是第二年的卫星观测数据,输出T1, T2是重构过程中每一步输出第二年的三维温度场。The inputs T, S are 3-D monthly-mean temperature and salinity in the past year provided by CMEMS, the inputs SST and SLA are satellite data in this year, and the inputs ARGO is the profiles in this year.The outputs T1, T2 are the reconstructed temperature fields in each step.)
图3 重构温度场的流程图
Fig.3 The flow chart illustrates the process of temperature reconstruction
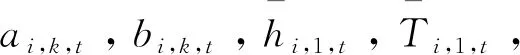
(3)


3.1.3 位势高度 在3.1.2 节中,y-1年份的海面位势高度可以通y-1年份的三维温盐场计算得到,这节将显示如何利用海面高度异常SLA来计算海面位势高度,用到的各个变量的含义显示在图4中。

(海面高度异常SLA(Sea Level Anomaly),平均动力高度 MDT(Mean Dynamic Topography),绝对动力高度ADT (Absolute Dynamic Height),位势高度GH (Geopotential Height),海表位势高度h(Surface Steric Height).)
图4 变量之间的关系
Fig.4 Diagram illustrates the relation
ADTy-1=MDT+SLAy-1,
(4)
ADTy=MDT+SLAy。
(5)
其中:y和y-1的意义和公式(3)中一样; SLA是AVISO提供的卫星观测的海面高度异常。GHy-1可以通过下式计算:
GHy-1=ADTy-1-hy-1。
(6)
其中,hy-1是y-1年份的海表位势高度,是由y-1年份的CMEMS的三维温盐场计算得到。那么y年份的海表位势高度:
hy-1=ADTy-GHy-1。
(7)
3.1.4 重构三维温度场 为了测试多元回归方程的重构三维海温的效果,选择利用CMEMS提供的2014年的三维月平均温盐场和2015年的卫星遥感数据来重构2015年的三维海温,并和CMEMS的2015年的三维海温数据做对比,并检测效果。因此公式(3) 中的y=2015 ,y-1 = 2014,公式(3)变成如下格式:
(8)


(其(a)、(b) 为2014和2015年CMEMS的月平均三维温度场的均方根差异;(c)、(d)为重构的2015年的月平均三维温度场和2015年CMEMS温度数据的均方根差异。(a),(b) is the RMS difference between the CMEMS monthly-mean temperature of 2015 and 2014. (c),(d) is the RMS difference of the reconstructed temperature field of 2015 and the 2015 CMEMS temperature field.)
图5 垂直和水平方向的均方根差异
Fig.5 The vertical and horizontal RMS difference
图5 (a)中, 深度方向的均方根差异从-1 000 m的0.3 ℃增长到-600 m的1 ℃,在-500 m为 1.5 ℃,最大的深度方向的均方根差异可以达到2 ℃。而5(c)中,深度方向的均方根差异在-600 m处值为0.5 ℃,且在-200 m以深,都保持在1 ℃以下。图5(b)中在西南部区域水平方向的均方根差异基本都大于1.8 ℃,而在5(d)中只有少部分区域的水平方向的均方根差异超过1.8 ℃。从上面的分析可得重构的温度场的精度还是较高的。
3.2 对比分析
3.1节中利用相邻年份的温盐数据建立了重构海温的回归关系,那么利用多年平均的温盐数据或者隔一年的温盐数据建立的回归关系来重构温度场的效果如何呢。为了做对比,利用多年平均的WOA温盐数据建立了回归方程,并以此重构了2015和2016年的三维温度场,它们和CMEMS的2015年的温度场的均方根差异如图6中的虚线所示。同时利用2014年的温盐场建立的回归方程重构了2016年的三维温度场,其和CMEMS的2016的温度场的均方根差异如图6中点线所示。利用相邻年份数据重构的2015和2016年温度场如图中实线所示。从图6的(a)(b)(c)(d)可见,利用多年平均数据建立的回归方程重构的温度场在-200 m以上比利用相邻年份重构的温度场精度高,但是在-200 m以下的温度场,利用相邻年份重构的温度场精度更高。从图6的(e)(f)可见,利用隔一年的温盐数据重构的温度场的精度在-150 m以上比利用相邻年份重构的温度场精度差,对-150 m以下的温度场,二者相似。故得利用相邻年份的温盐数据建立的回归方程重构温度场具有一定的优势。
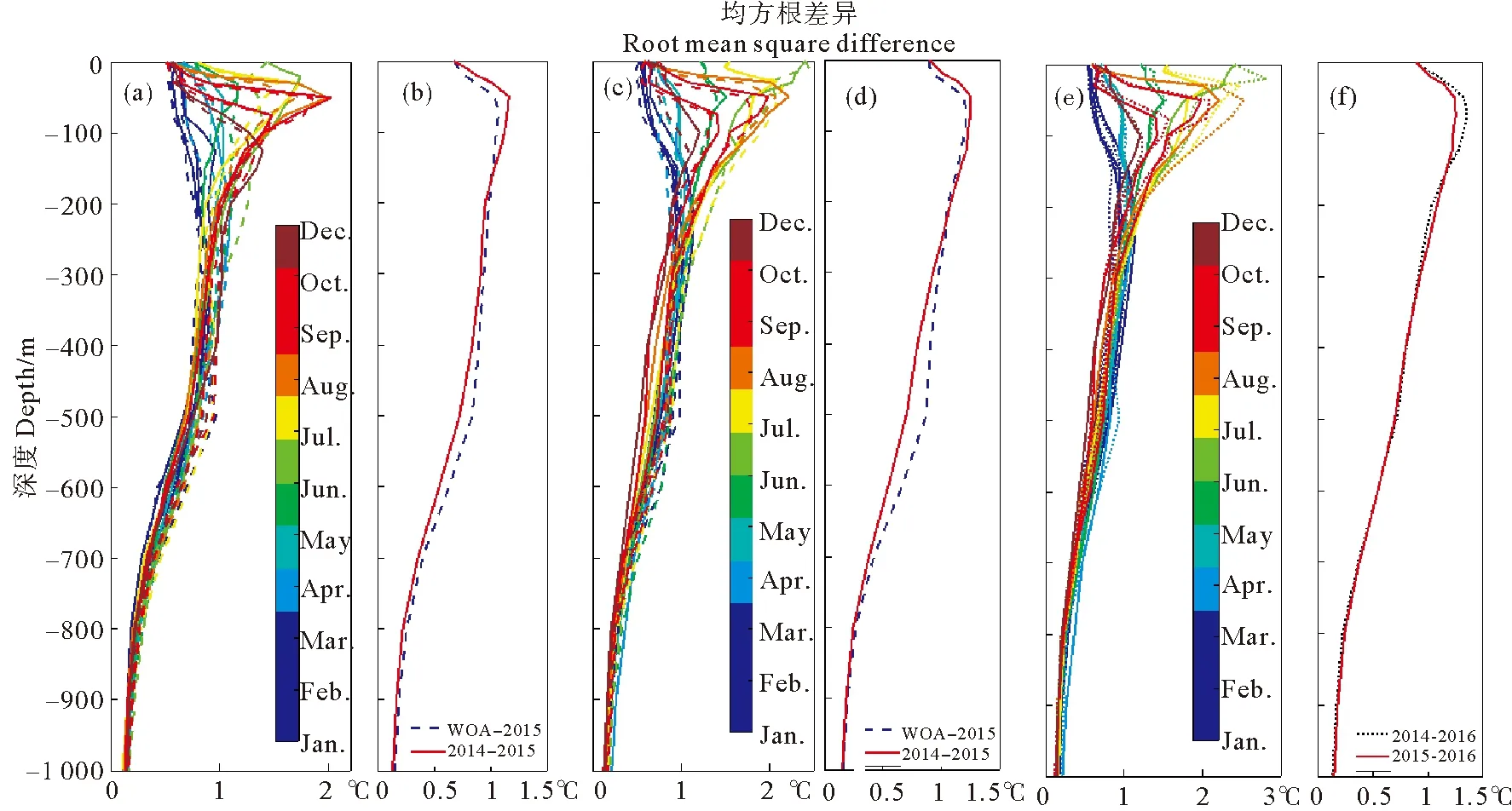
(其中(b)、(d)、(f)分别为对应于(a)、(c)、(e)的年平均值。(b)、(d)、(f)corresponding to the annual average of (a)、(c)、(e).)
3.3 同化Argo数据
Argo观测温度剖面数据在该区域比较丰富,重构的温度场可以同化它以提高精度。本项目选择最优插值(Optimal interpolation,OI)同化方法,该方法简单高效,是使用频率较高的同化方法[14]。从图7(a)中可见,经过同化ARGO观测值的2015年重构温度场在次表层的大部分月份的均方根误差都小于1.5 ℃。在深度200 m以下,垂直方向上的12个月的重构温度场的均方根误差都小于1°。从均方根误差的水平分布图7(b)来看,大部分区域都小于1 ℃,只有极少数区域超过1.5 ℃。对比图5和7,发现同化后的温度场确实提高了精度。
至此共存在三种温度场:利用回归方程重构得到的2015年的三维温度场,OI同化吸收Argo观测值后的温度场以及CMEMS的温度场。把它们分别插值到Argo观测点上,并比较它们的值和Argo观测值。从图8可见经同化后的重构温度廓线和Argo观测廓线较接近,表示重构的温度场的精度是可接受的。
3.4 重构的温度场、CMEMS温度场和观测值比较
本文重构月平均三维温度场依赖于相邻的年份的温盐场,因为相邻年份的数据之间有很强的相关性,同时均方根差异也越小。例如2014和2015年的CMEMS的三维温度场之间的相关系数为97.92%,2015和2016年之间的为 97.97% ,2014和2016年之间的为97.86%;各自之间的均方根差异分别为1.32,1.33和1.37 ℃。图1中的第一步利用由前一年的温盐场得到的回归方程来重构得到的三维温度场要比利用多年数据来重构温度场要更有效。CMEMS的三维温度场是基于长时间序列计算得到的。把CMEMS的温度场和本文重构的温度场插值到有Argo观测的温度廓线的地点,并分别计算它们和Argo观测的温度廓线之间的均方根误差,结果显示在图9中。从图9可见,2015年的CMEMS的温度场与Argo温度廓线的均方根差异比重构的温度场和Argo温度廓线的均方根差异要大近0.2 ℃。2016年二者的差距更大,这说明本项目的重构的结果比CMEMS的温度场略好。

图7 垂直和水平方向的均方根差异Fig.7 The vertical and horizontal RMS difference
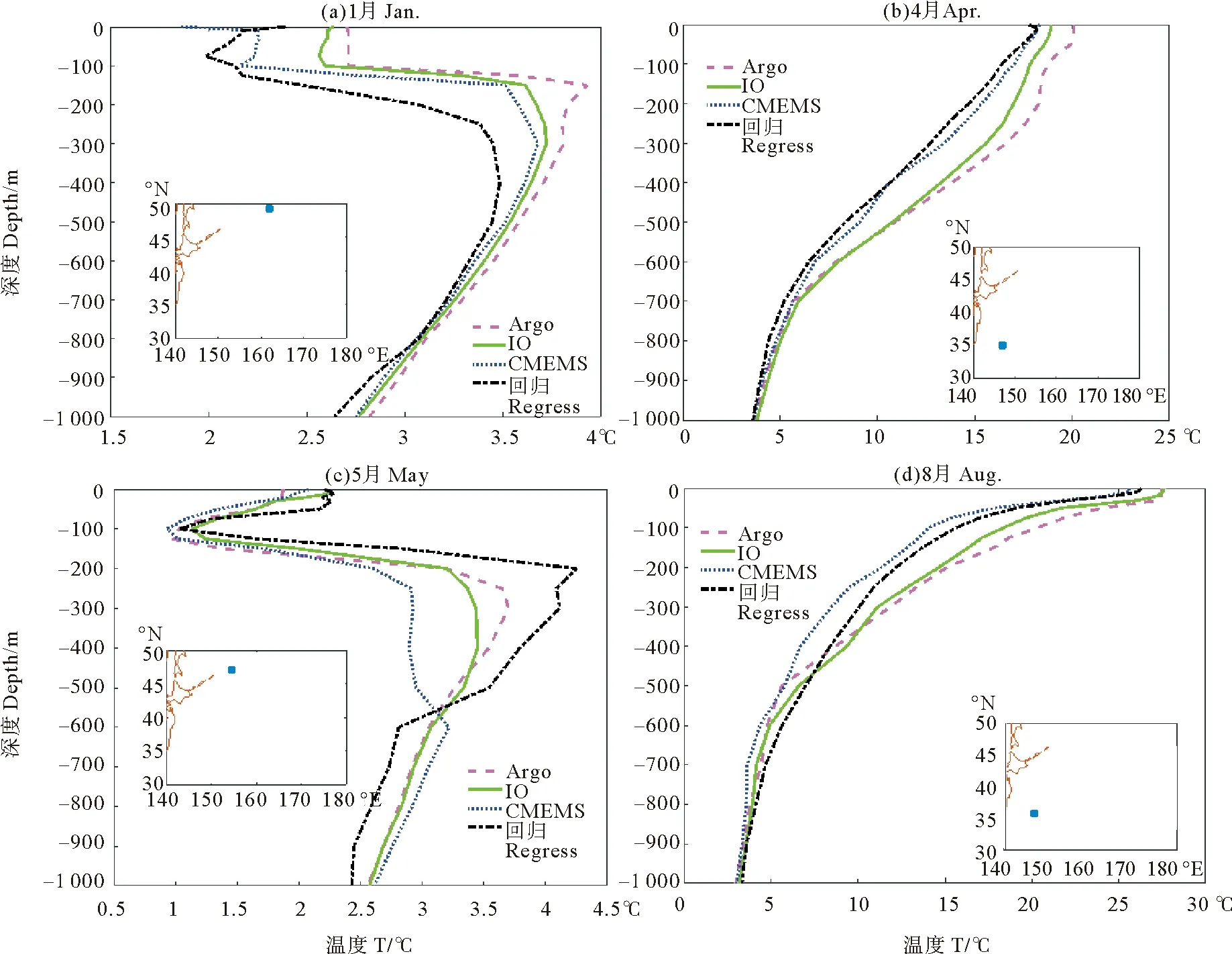
(其中小图的蓝色点表示argo观测的位置,彩色曲线表示插值所得的温度廓线。The position of the ARGO observation for each figure is shown by the corresponding blue point in the small figure.)
图8 温度廓线
Fig.8 Temperature profiles

图9 2015和2016年重构的温度、CMEMS温度数据与Argo观测值的均方根差异Fig.9 The RMS difference between Argo observation and reconstructed temperature,temperature of CMEMS during 2015 and 2016
4 结语
本文建立了一种重构三维温度场的方法,重构了流程。该方法基于相邻年份的3维温度场来重构,因为相邻年份的三维温度场之间有很强的相关性。例如,2014和2015年的CMEMS三维温度场的相关系数为97.92%,均方根差异为1.32 ℃;2015和2016年为97.97%,均方根差异为1.33 ℃;2014和2016年的为97.86%,均方根差异为1.37 ℃。按照图1的流程,利用2014年的CMEMS三维温度场重构2015年的温度场,第一步的结果即通过线性回归方程重构后所得结果和CMEMS温度场的相关系数为99.09%,均方根差异为0.88 ℃。第二步加入Argo同化后的重构温度场与与CMEMS温度场的相关系数为99.29%,均方根差异为0.79 ℃。利用2015年的CMEMS三维温度场重构2016的温度场的这二步的相关系数分别为:98.94%、99.12%,均方根差异分别为0.99和0.89 ℃。所以利用前一年的三维温度场来逐月重构当年的温度场是可行的。
重构的三维温度场在200 m以下具有较好的精度,垂直均方根误差小于1 ℃,在次表层垂直均方根误差超过1°C。从7 —9月,重构温度场的均方根误差比其他月份大。水平的均方根误差分布不均匀,在大部分区域都小于1 ℃,在少数区域超过1.5°。所以如果在那些均方根误差较大的地方的次表层,存在从可能少数字月至9月的观测数据,那么重构的温度场就可以同化吸收这些观测值从而可以进一步提高精度。
致谢:Argo观测的温度剖面数据由国际Argo项目组提供,下载地址:ftp://ftp.ifremer.fr/ifremer/argo/dac/。三维月平均温/盐场由CMEMS 负责制作和发布,下载地址:http://marine.copernicus.eu。
附录
a.位势高度
在温度T,盐度S和压力p处,单位重量的海水体积为:
(1)
δ(S,T,p)=α(S,T,p)-α(35,0,p)。
(2)
叫做特征体积异常。动力高度φ(相当于大气中的重力势)表示从给定的位置垂直移动单位体积的水体至海面所要做的功,单位为J/kg或者m2/s2。相对于海面高度的φ表达式如下:
(3)
从静力学公式
p=-ρgz
(4)
可以导出如下关系式:
(5)
其中:g表示重力加速度;z向上增长。动力高度φ和动力高度异常ψ的关系能够被推导出,如下

(6)
该式表明动力高度异常等于重力势φ减去一个压力函数。动力高度异常可通过下式计算:
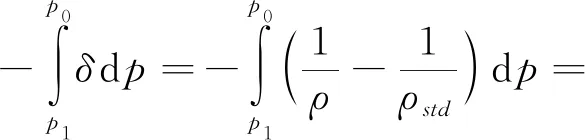
(7)
重力加速度可以设为在45°N的中的值9.806 65 m/s2,因此位势高度可以定义为:
(9)
它是具有长度单位米的地转流函数。位势高度可以和卫星观测的海面高度异常集合,来计算某一深度至大地水准面之间的重力势高度。

