基于信息融合的炸点图像坐标估计方法研究
刘鹏祖,王明启,徐韬祜,柴如兴
(中国人民解放军63875部队, 陕西 华阴 714200)
炸点坐标测试是常规靶场最重要的测试项目之一[1-2]。利用炸点图像正确估计出炸点的像空间坐标,是炸点坐标光学测量技术中的关键环节[3]。依据目标爆炸时爆炸中心(后简称“爆心”)相对地面的位置,炸点可分为高空炸点和近地炸点[4]。高空炸点在爆炸过程中不受地面干扰,而近地炸点的爆炸物在膨胀过程中受地面阻挡或地表物遮挡,成像的形状不规则。近炸引信作用时距地面较近,在靶场植被较高或爆炸点处于低洼地等条件下,爆炸物可能会触地或被地表物部分遮挡,导致爆炸火光在第一帧成像时已发生畸变或部分被遮挡。现有的炸点测量系统采用质心法求爆心的像空间坐标,该方法对于高空炸点能实现高精度定位,然而对于受地面干扰的近地炸点,火光质心与爆炸中心不一致,甚至差别较大,则定位精度会大幅度下降。因此,需要研究新的方法,提高受地面干扰的近地炸点像空间坐标估计精度,为炸点坐标高精度测量提供技术支持。本文后续所提的坐标特指像空间坐标。
1 基于质心法的炸点图像坐标处理方法
质心坐标计算方法为:
(1)
式(1)中,f(x,y)为目标图像各像素点的灰度值;∑表示在目标区域R内求和。
图1为某型高速相机在8 000 fps时拍摄的近炸引信炸点图像。
该组试验的目标炸高为5~7 m,对7发目标数据处理结果如表1所示。
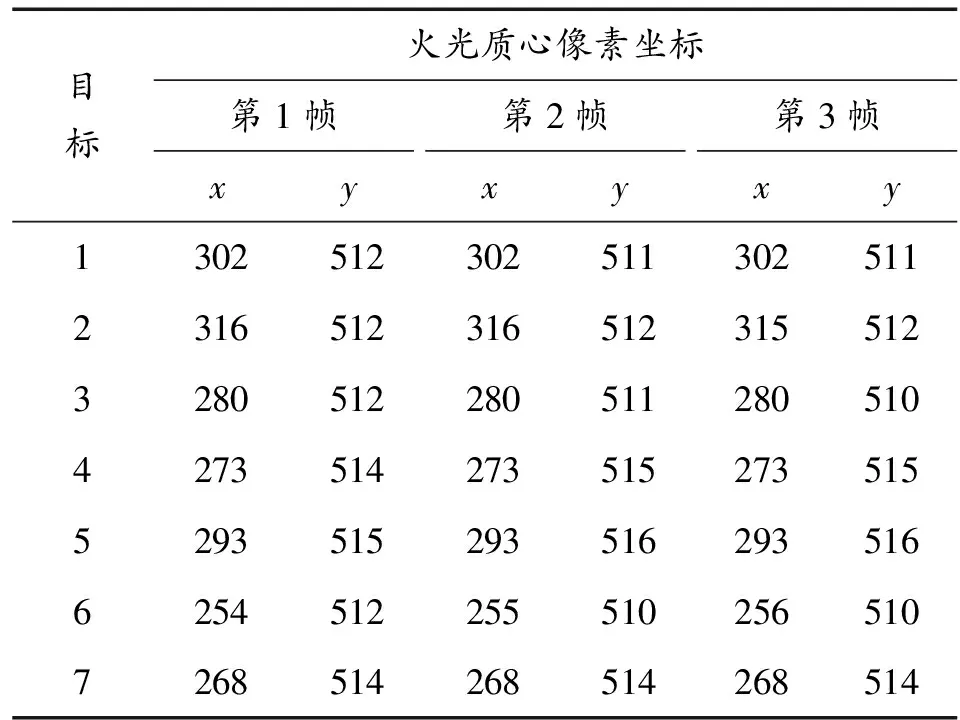
表1 数据处理结果
表1中x,y为火光质心的像素坐标,坐标原点(0,0)位于图像的左上角。从表1中的数据可以看到,前3帧火光质心坐标极差在各方向上均为2,变化量很小。
图2为某型高速相机在8 000 fps时拍摄的某发近炸引信炸点图像。第1帧为爆炸初期形态,爆炸物成像时无遮挡,体积相对较小,质心位置近似为爆炸中心位置;在第2帧,爆炸物膨胀充分,部分火光被地表植被遮挡,导致爆炸火光成像不完全。数据处理结果如表2所示。

图2 炸点图像

处理对象特征火光质心坐标xy第1帧火光近似为圆733.83192.50第2帧火光部分火光被庄稼遮挡724.13201.69
表2中数据表明,前后两帧质心坐标的变化量在各方向上都接近10,变化量较大。如果第一帧没有被捕获,采用第二帧作为处理对象,则误差偏大。其原因主要是:火光下半部分被遮挡,图像并不是规则的圆,图像质心并不是爆炸中心。
综合以上分析可知:对于近地炸点,受地表影响,爆炸物部分被遮挡或阻挡时,采用质心法求解导致测量误差较大。
2 基于信息融合的炸点图像坐标估计模型
在高速像机所拍摄的序列图象中,设弹丸在第n帧爆炸,爆炸点坐标记为Xn,要求的目标即为Xn的值。对正常成像的目标,Xn可通过质心法获取;对非正常成像的目标,则需要通过计算间接得到。
设Xn-1为爆炸前一帧的弹丸质心坐标,ΔX表示Xn相对Xn-1的位置差,即:
Xn=Xn-1+ΔX
(2)
通过对以往试验数据的大量分析可知,ΔX可基于同一组试验中的正常成像的目标数据进行估计;Xn-1可以通过末端弹道线性拟合和预测获得。模型实现的总体框图见图3。
3 算法实现
3.1 算法流程
算法流程框图如图4所示。
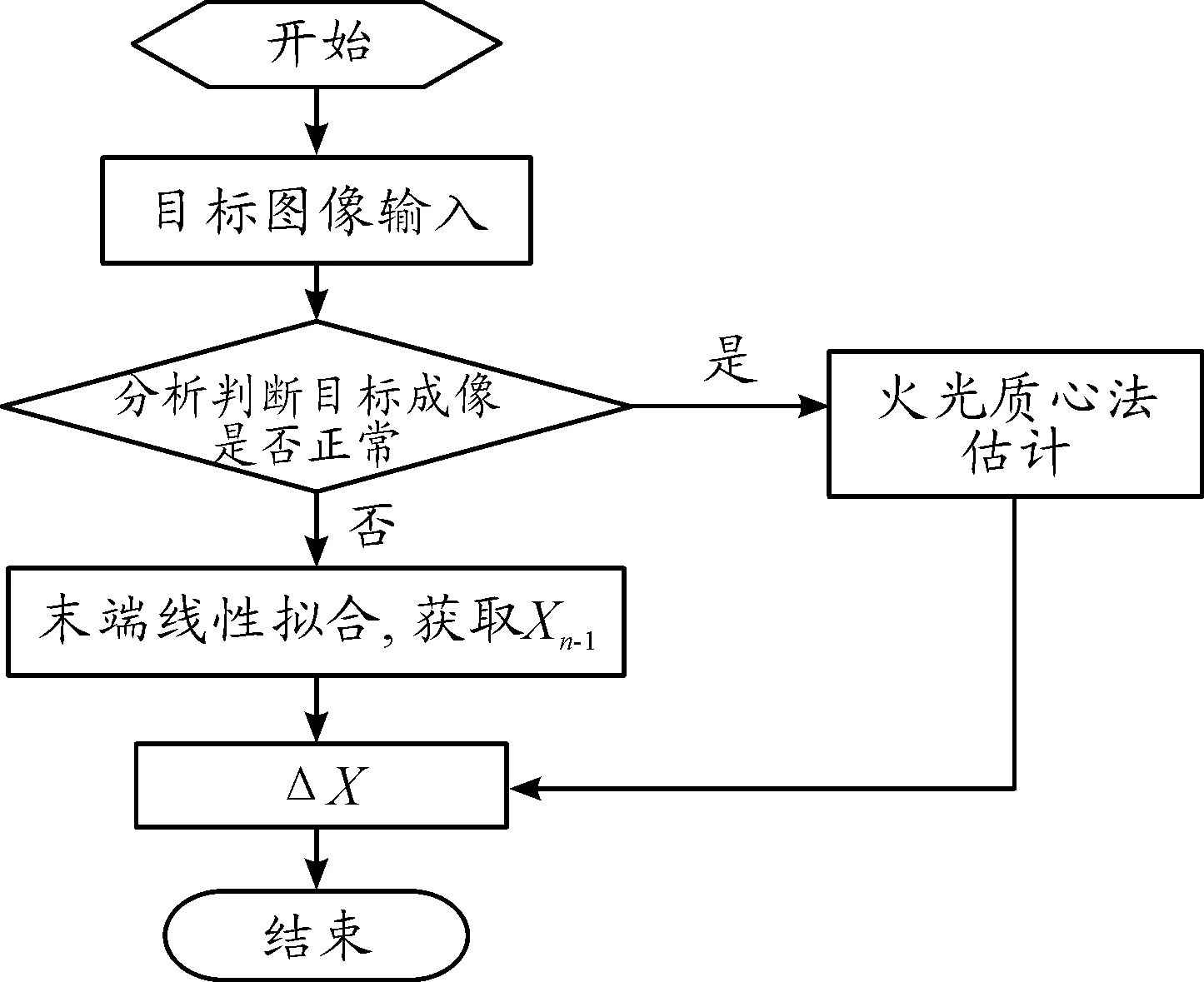
图3 总体框图
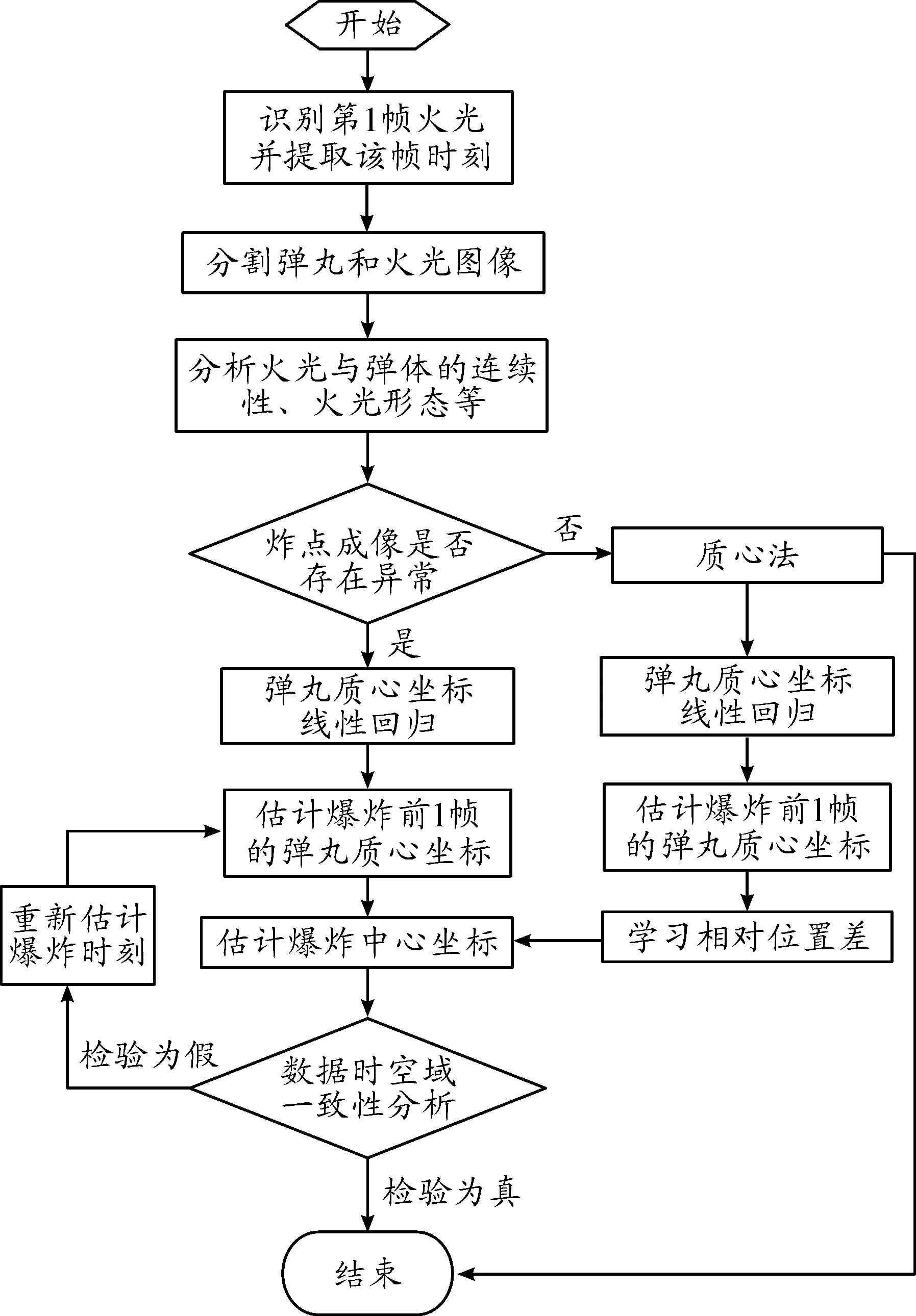
图4 算法流程框图
主要步骤介绍如下:
步骤1基于爆炸火光出现的突变性,采用减背景方法[5]和形态滤波方法[6],检测识别出第一帧出现火光的图像,获得相对时刻Tn;
步骤2采用减背景方法、窗口滤波方法和双阈值方法[7],识别爆炸火光出现前7帧弹丸图像,并计算弹丸质心坐标[Xn-7,Xn-6,…,Xn-1],记录对应的相对时刻[Tn-7,Tn-6,…,Tn-1];
步骤3分析第一帧火光是否为圆;分析第一帧火光前的弹体是否存在;
步骤4根据步骤3的分析结果判断炸点成像是否异常;
步骤5成像正常,则采用质心法计算炸点图像坐标,并计算输出修正值ΔX;否则跳转步骤6;
步骤6基于步骤2的数据,采用线性回归方法估计弹丸质心坐标运动方程[8];
步骤7假设步骤1获得Tn为爆炸时刻;
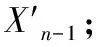
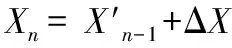
步骤10对估计结果进行数据时空一致性检验,检验为真则结束;否则,重新假设目标爆炸时刻,并跳转步骤8。
基于Matlab软件平台编写了算法应用软件。软件界面如图5所示。
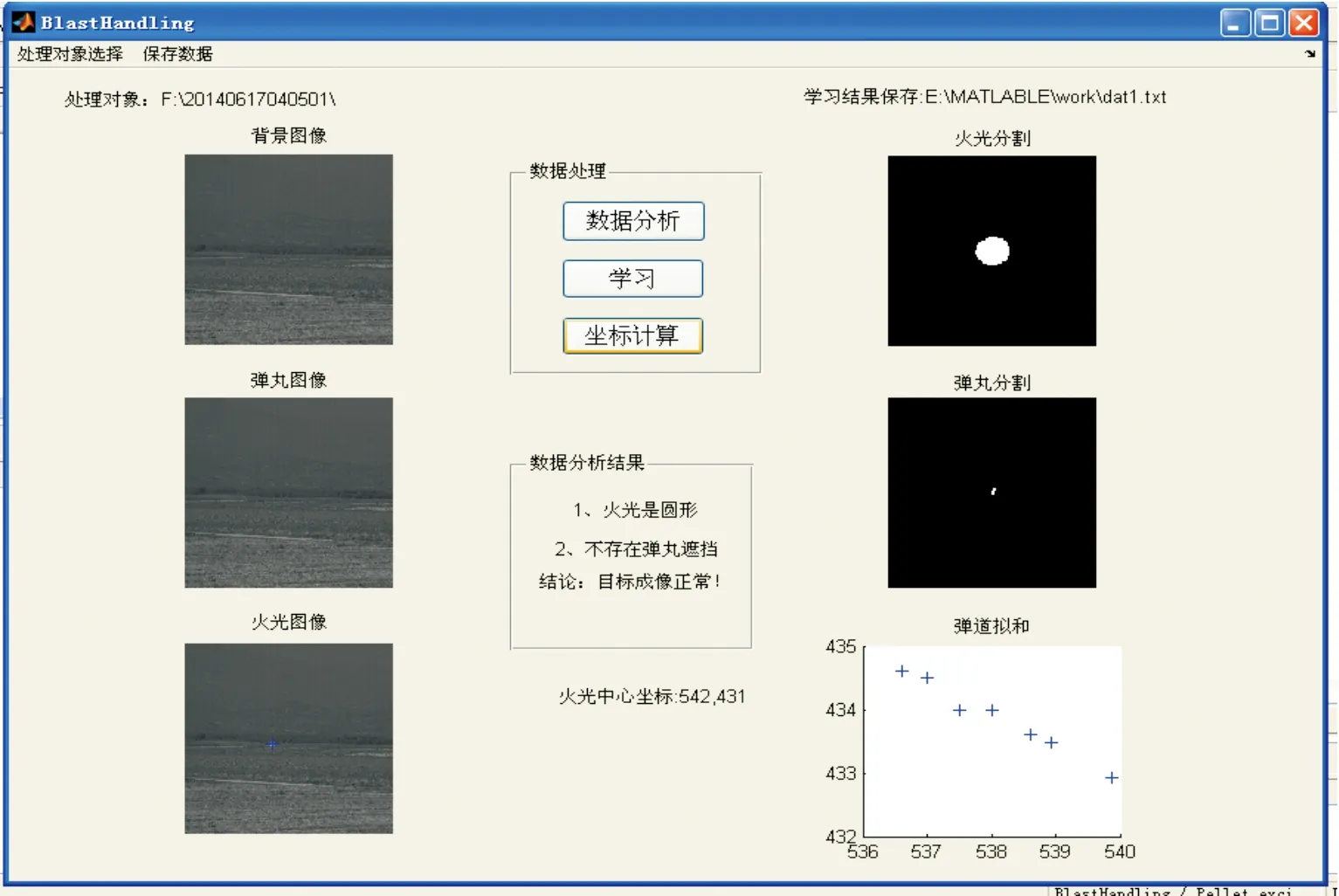
图5 算法流程软件界面
3.2 炸点图像分析判断
根据已往的研究可知,在帧频大于1 000 fps条件下,正常成像的炸点火光在第一帧的成像近似圆形[9]。因此,可对火光图像进行圆形检验[7],检验结果为圆形,说明目标成像正常,检验结果不是圆形,则说明目标成像不正常。但该条件只是必要条件。对以往数据分析可知,大多数目标落速不超过300 m/s,当图像采集帧频大于1 000 fps时,爆炸点和爆炸前一帧弹丸位置变化不大,如果前一帧弹丸被遮挡,则爆炸点被遮挡的概率很大。
因此,建立判断准则为:当火光图像检测为圆形,同时前一帧弹丸成像未被遮挡时,判断为炸点图像正常;否则,判断为炸点图像异常。
3.3 弹丸质心坐标线性回归分析
估计模型需要获得弹丸Tn-1时刻的质心坐标Xn-1。由于弹丸图像为暗弱目标,精确提取较难,单帧弹丸图像的质心定位精度难以满足需求,因此,采用线性回归分析提高Xn-1的处理精度。
由于高速摄像机的帧频高达1 000 fps以上,在0.01 s时间内,认为目标进行匀速运动是合理的。为了验证该假设,选取一次试验的数据并进行分析。
通过图像处理技术能求取得到弹丸目标在一个不同位置的质心坐标如表3所示。
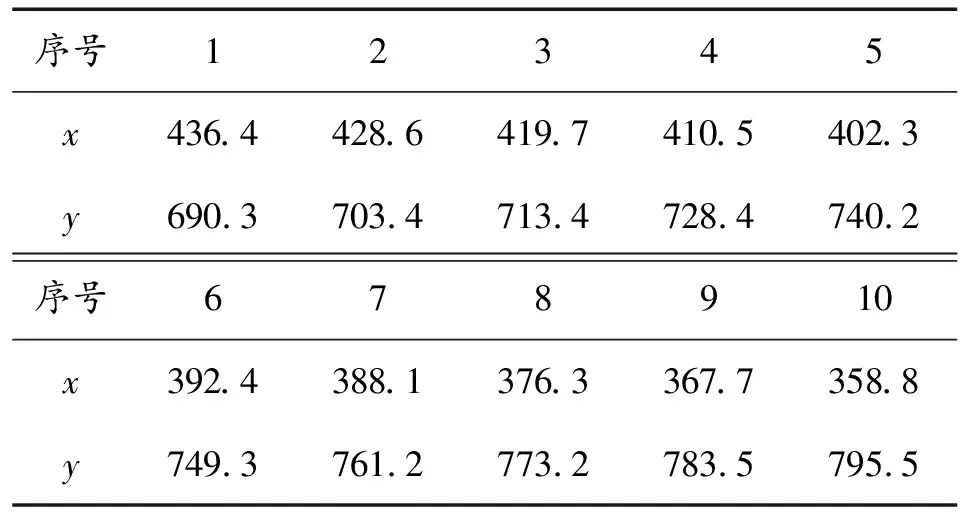
表3 目标质心坐标
对表3中的数据,以序号作为预测变量,坐标分别作为相应变量,做最小二乘线形回归,回归方程分别有:
x=-8.599t+445.3R2=0.998
(3)
y=11.59t+680.0R2=0.998
(4)
时间对质心坐标的散点图和拟合的最小二乘回归直线如图6所示。
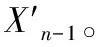
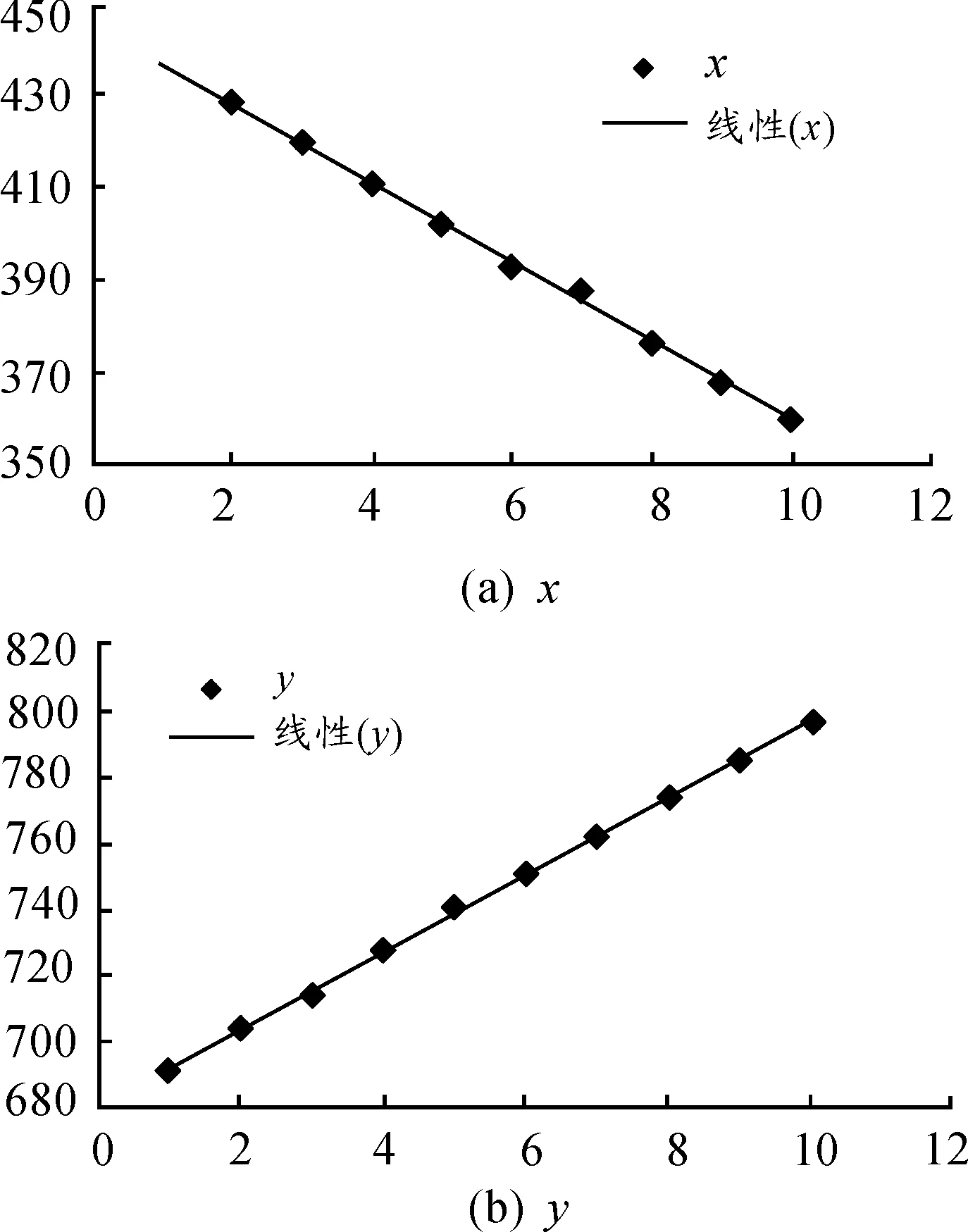
图6 时间对质心坐标的散点图和拟合的最小二乘回归直线
3.4 爆心与弹丸的相对坐标计算
对于某一组弹丸,爆炸中心与爆炸前一帧弹丸质心具有较稳定的相对位置关系,但由于爆炸时刻和拍摄的随机性,每一个目标的爆炸中心与前一帧弹丸质心坐标相对位置同样具有随机性。通过对多个正常成像目标的数据进行学习,可估计得到相对位置的均值估计值。表4举例了该学习方法,表4中以3个正常成像目标为学习样本,学习相对位置。
对三个学习样本的相对位置求平均值为[1.2、1.2]。
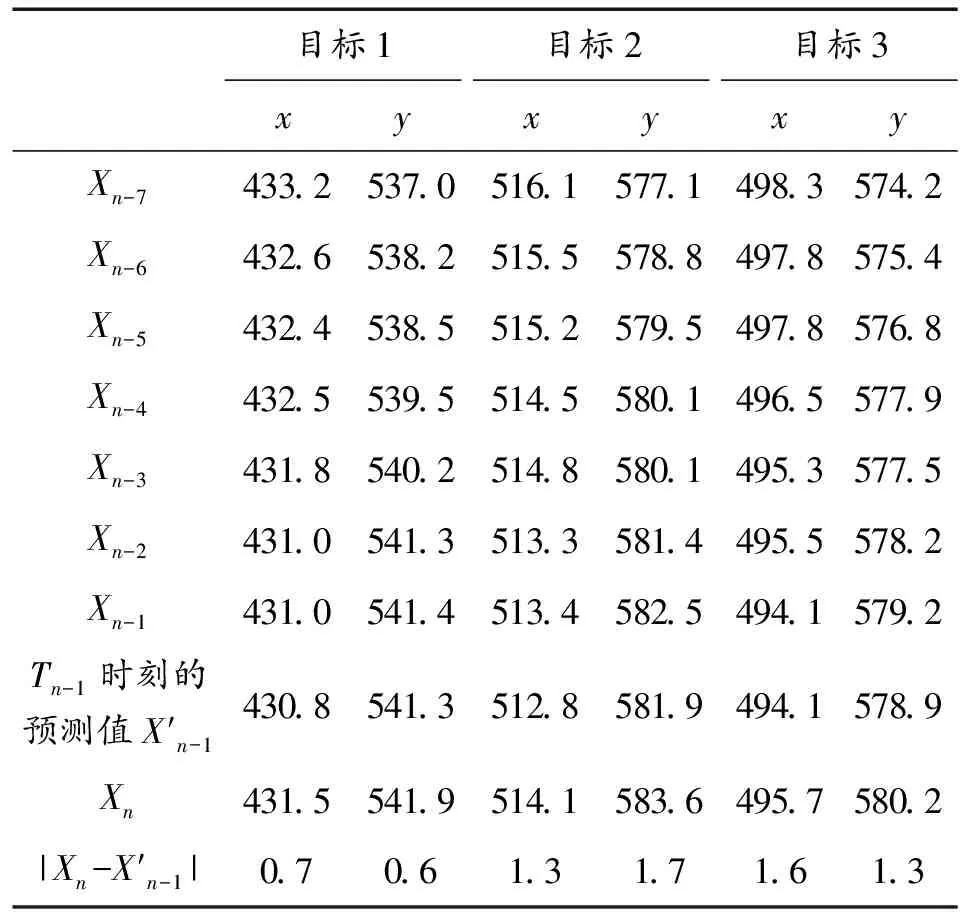
表4 爆炸中心与弹丸质心坐标
3.5 目标作用时刻修正方法
3.5.1修正方法
该文拟采用迭代方法估计准确的爆炸时间。首先假设爆炸火光第一帧的成像未被完全遮挡,基于弹丸图像信息和爆炸火光时刻信息得到爆心位置第一次估计值;然后根据爆炸火光图像膨胀速度近似模型,计算爆心位置第一次估计值和爆炸火光尺寸在时空域上是否一致性。判断式如下:
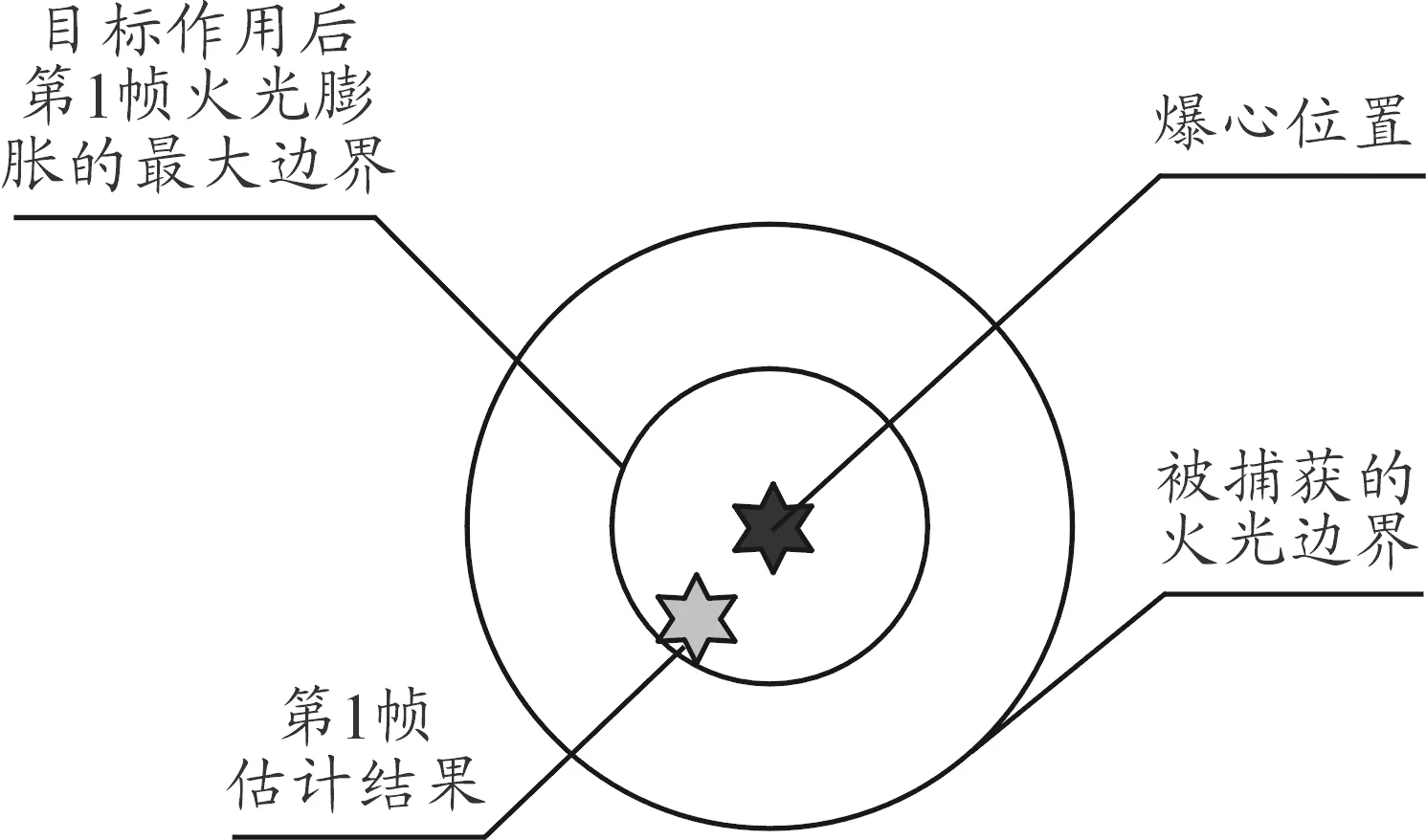
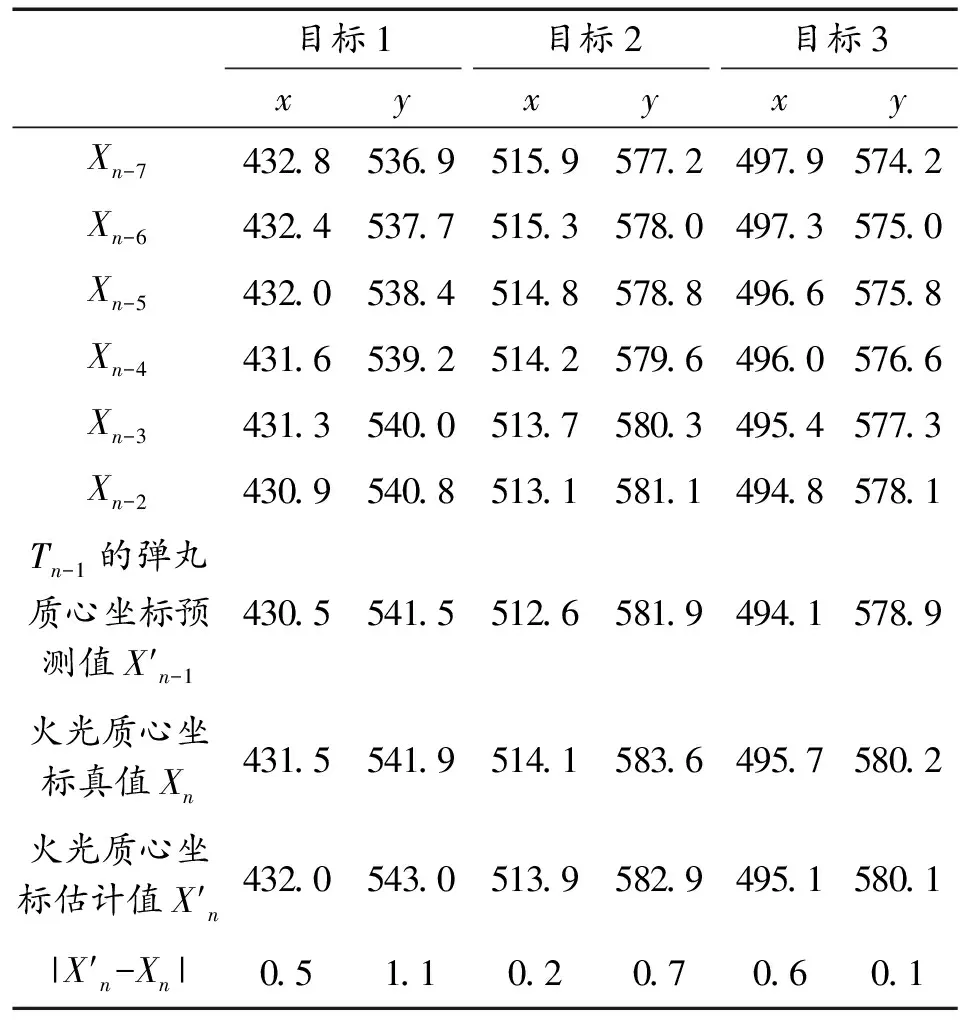
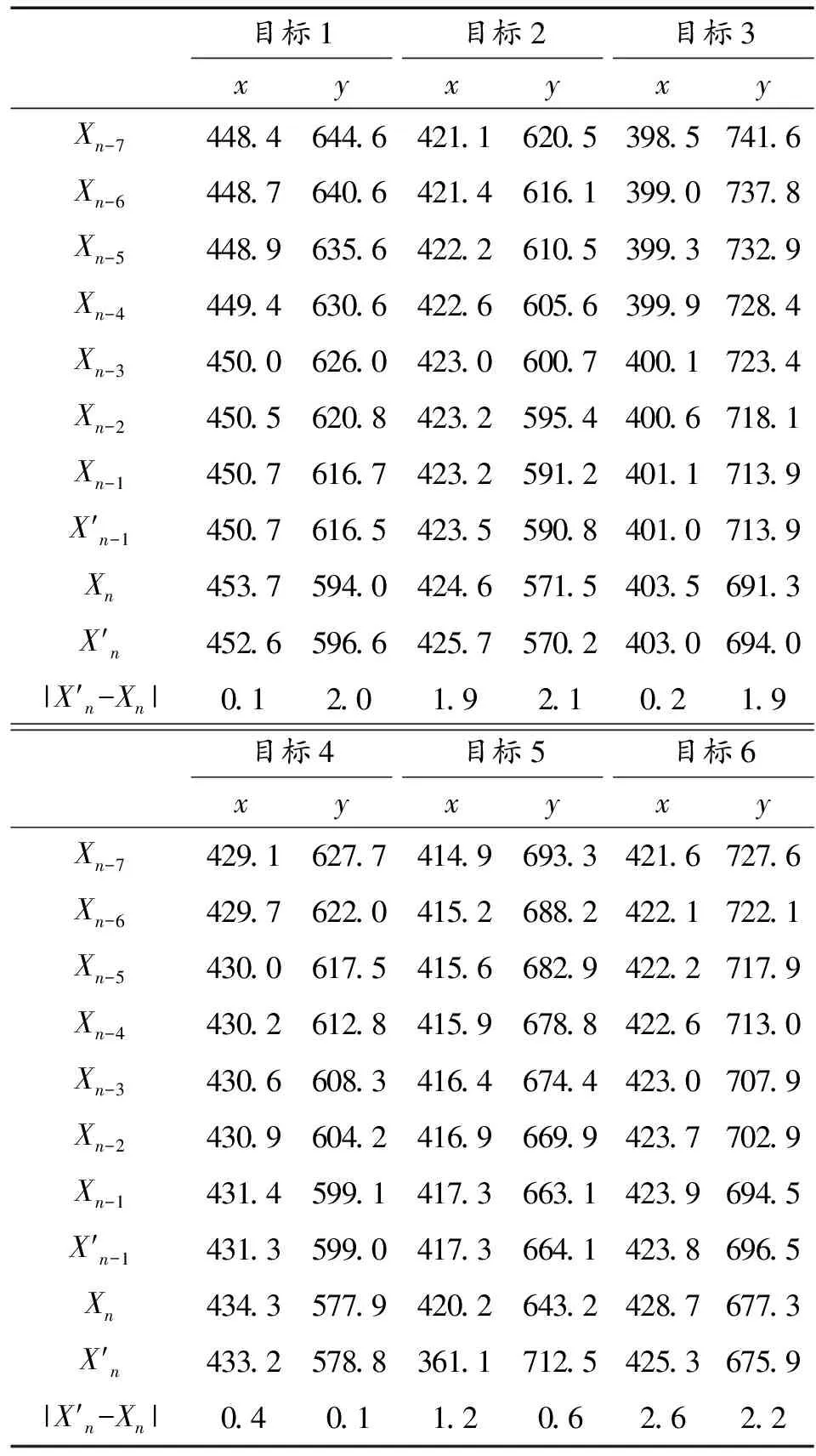
Rmax 其中Rmax(火光各点到爆心坐标估计值的距离);Ri表示爆炸火光图像经过i帧时间后膨胀的大小,基于同一种弹的火光膨胀速度试验样本数据估计获得。 根据假设,第一帧图像未被遮挡,则取i=1,进行判断,若判断为真,则假设正确,火光为第一帧,若判断为假,修正爆炸时刻,i=i+1,重新估计爆心位置。这样,通过反复迭代方法估计出更加准确的爆炸时间,直至爆心位置估计值和爆炸火光尺寸在时空域上一致。爆炸火光示意图见图7。 图7 爆炸火光示意图 3.5.2迭代收敛性分析 在近炸引信试验中,弹丸的末端运动速率一般小于1 000 m/s,爆炸火光的膨胀速度约8 000 m/s,即在一帧时间,爆炸火光成像半径的变化是弹丸图像质心位置变化的8倍以上,如图8所示。下面通过数据分析说明收敛过程,假设被拍摄到的火光是第N帧的火光,时间为T0,真实的火光半径R0,R为前后两帧的火光半径近似值。 图8 第1帧火光估计结果示意图 第一次定位为X1,当N小于8时,在第一次定位的基础上计算获得火光半径估计结果R1为: RN (5) 则求的时间差为: TN (6) T1基本接近真值,将该时刻进入迭代计算,第二次定位结果为X2,通过X2求得: RN-1 (7) TN-1 (8) T2基本接近真值,将该时刻进入第二次迭代计算,第三次定位结果为X3,通过X3求得,即: RN-1 (9) R3的计算结果与R2一致,则迭代结束。 试验数据分析表明:对近炸引信装配的常规弹丸,测量相机在1 000 fps以上时,火球正常膨胀一般约4帧以内结束因此,该数据分析证明结果合理。 对成像异常的目标,根据炸点图像坐标获取方法可知,坐标估计结果的误差由数据处理误差和估计模型误差两部分组成。 对估计模型进行推演如下: (10) 下面对Xn-1的标准误差进行推导。根据参考文献[9]可知,可假定弹丸图像质心坐标的误差ε相互独立,并且都服从均值为0,方差为σ的正态分布,即εi~iidN(0,σ2),σ2>0。σ2的一个无偏估计[10]为: (11) (12) (13) (14) 2014年某型试验,图像采集帧频为2 000 fps。试验数据(见表4)。 验证方法:假设爆炸前一帧弹丸图像已经被遮挡,该帧弹丸图像坐标缺失;爆炸物部分被遮挡,然后采用本文方法进行处理。 首先对每一个目标的6个弹丸质心坐标进行线性回归,预测出爆炸前一帧弹丸图像坐标;其次,对另外两个目标的坐标差求平均,获得修正值;最后,将修正值与预测值相加,得到火光质心坐标估计值。如表5所示,最后给出了估计误差绝对值。 从表5试验数据处理结果可知,平均估计误差为0.53个像素。根据试验设置可知0.53个像素对应约5 cm误差。 该次试验数据处理由于可用的样本量少,导致误差稍偏大。 表6为2015年某型试验,该试验采用高速摄像系统进行了拍摄,可验证本文的基本算法(处理方法除了不假设爆炸前一帧弹丸图像被遮挡,其他同试验1)。 表5 估计结果及其误差 表6 数据处理结果 从表6试验数据处理结果可知,平均估计误差为1.3个像素。根据试验现场参数设置可知1.3个像素对应约2.6 cm误差。 本文提出了一种基于信息融合处理的炸点图像坐标估计方法,建立了融合估计模型,给出了算法流程,分析了测量误差,在Matlab软件平台上编写了实现程序,并利用试验数据对该方法进行了检验,结果证明该方法正确,对爆炸物非正常成像的炸点目标能实现像空间坐标的准确估计,为炸点坐标高精度测试提供了技术支撑。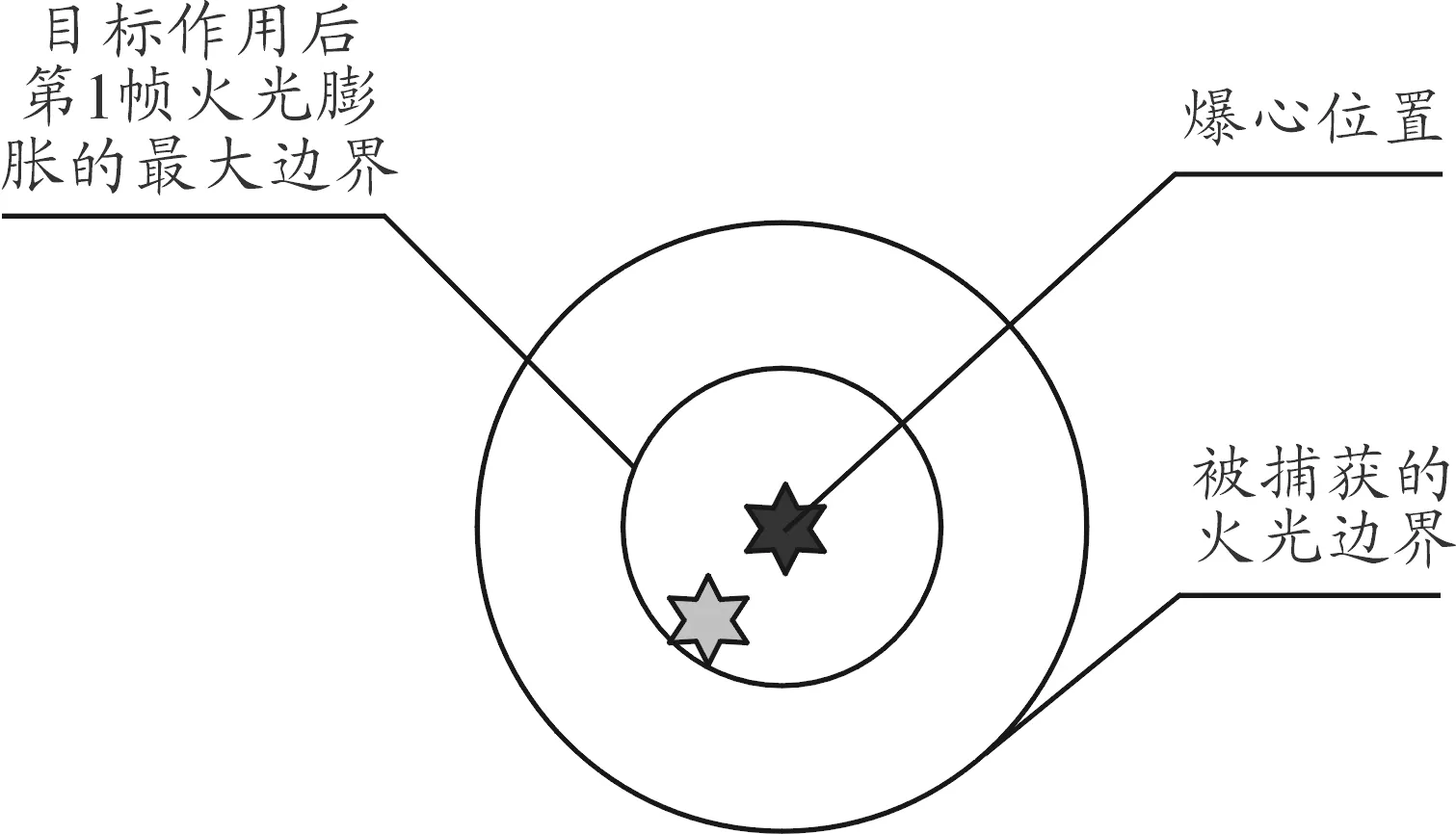
4 误差分析
4.1 数据处理误差
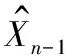
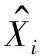
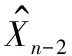
4.2 模型误差
5 方法验证
5.1 试验1
5.1 试验2
6 结论

