基于质量替换法的刨煤机系统动态特性分析*
张 瑜, 毛 君, 陈洪月, 郝志勇
(1.安阳工学院机械工程学院 安阳, 455000) (2.辽宁工程技术大学机械工程学院 阜新, 123000)
1 问题的引出
刨煤机作为一种浅截深采煤机械,具有刨落煤块大、工作效率高、结构简单和便于操作维修等特点,在世界各国用于开采薄煤层、极薄煤层[1-4]。目前,国内外学者对刨煤机的动态特性进行了大量研究。Ahrens[5]针对刨煤机系统动力学问题,以两端驱动链轮及刨头为分界点,将整体分为3部分,刨链采用弹簧单元描述。刘芮葭[6]基于连续系统振动理论,建立了刨煤机系统动力学模型,分析了系统的动态特性。李晓豁等[7]针对刨煤机工作面存在倾角、中部槽存在转角等问题,采用有限元方法研究了刨煤机系统的动态特性。文献[8-9]基于有限元法建立了刨煤机系统单自由度、多自由度动力学模型,并对两种模型条件下的系统动态特性进行了对比分析。张东升等[10]基于多体动力学理论建立刨煤机系统动力学模型,研究了驱动链轮轴的水平振动、链轮多边形效应等因素对系统动态特性的影响。文献[6-9]采用有限元方法建立的刨煤机系统动力学模型如图1所示,其状态方程如式(1)所示。其中:质量m1,m3为关于刨头振动位移的函数。当刨头沿图1所示方向移动时,将出现质量m3为零的情况,当刨头反向移动时,将出现质量m1为零的情况。可见,采用式(1)方法研究刨煤机系统动力学特性出现求解结果发散。

图1 修改前动力学模型Fig.1 Dynamic model before modified
(1)
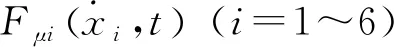
为更精确地分析刨煤机系统动态特性,综合考虑刨头移动、刨头与滑架体的间隙、刨链预紧力及链轮多边形效应等因素,笔者建立了刨煤机系统纵向振动-刨头碰撞振动共生时变动力学方程,研究工况条件下刨煤机系统动态特性,为刨煤机系统工作稳定性、关键零部件的疲劳寿命及工艺参数优化提供理论基础。
2 刨煤机系统动力学模型
2.1 动力学模型建立
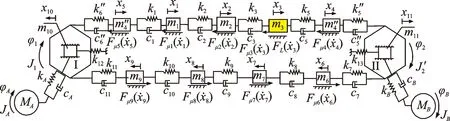
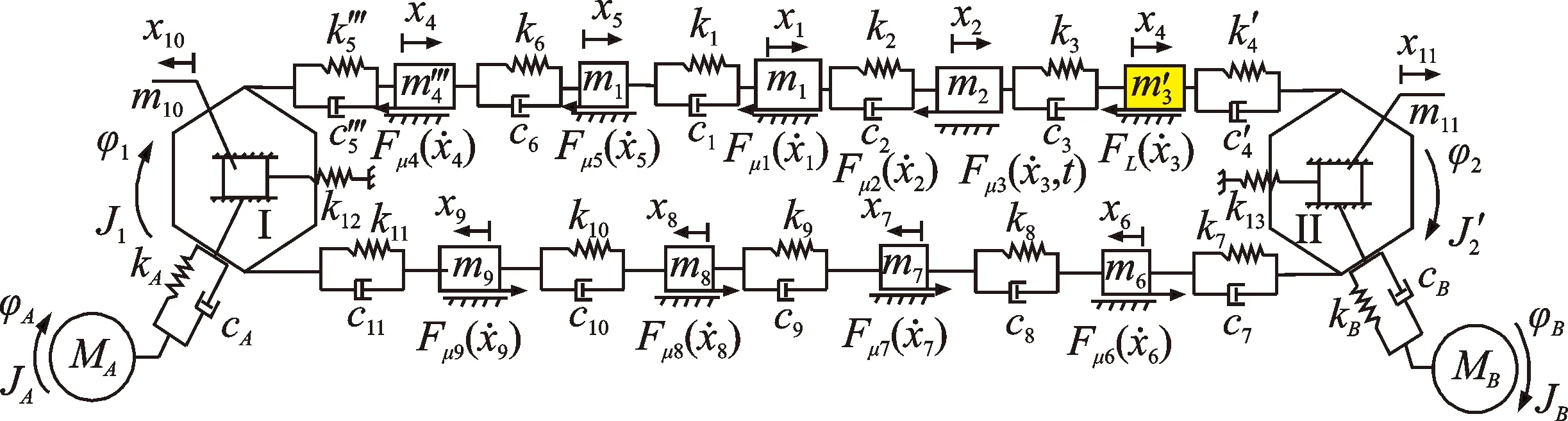
根据刨煤机的结构特点及工作特性,其物理模型如图2所示。将刨煤机系统进行离散化,刨头简化为较大的质量块,刨链离散为多个集中质量单元,各质量单元之间采用Kelvin-Vogit模型连接[11-12],本研究将刨煤机刨链系统划分为8个质量单元,令刨煤机系统工作面长度为L,系统有限元动力学模型如图3所示。
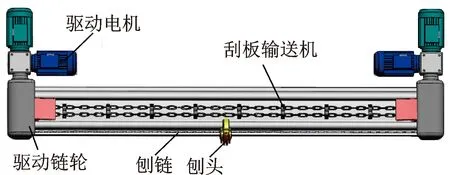
图2 刨煤机系统物理模型Fig.2 Physical model
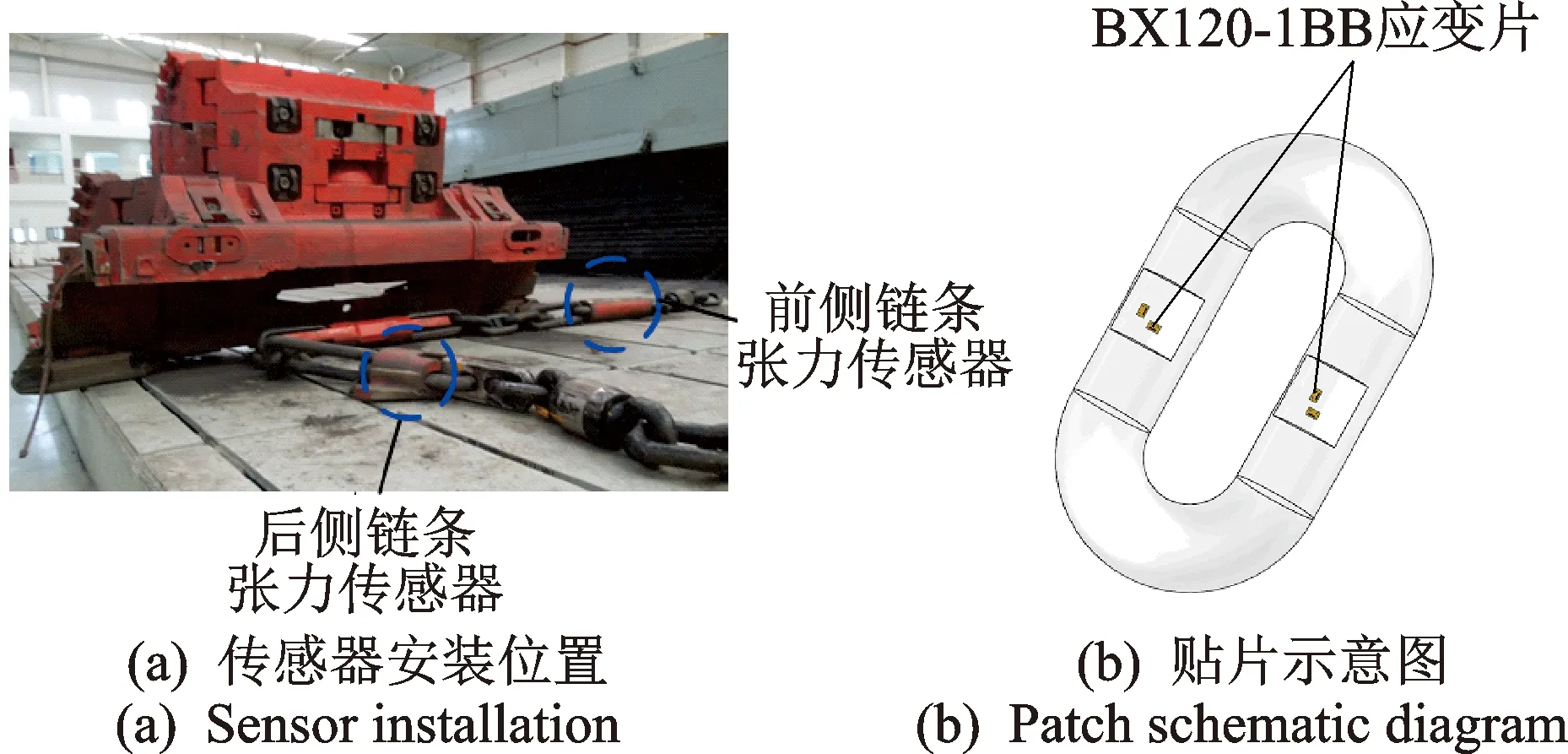
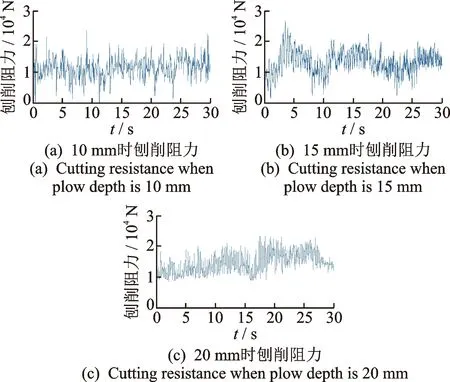
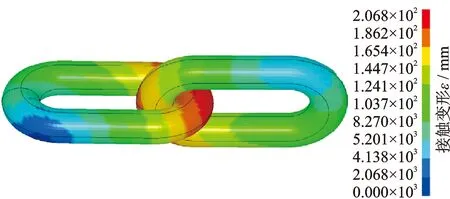
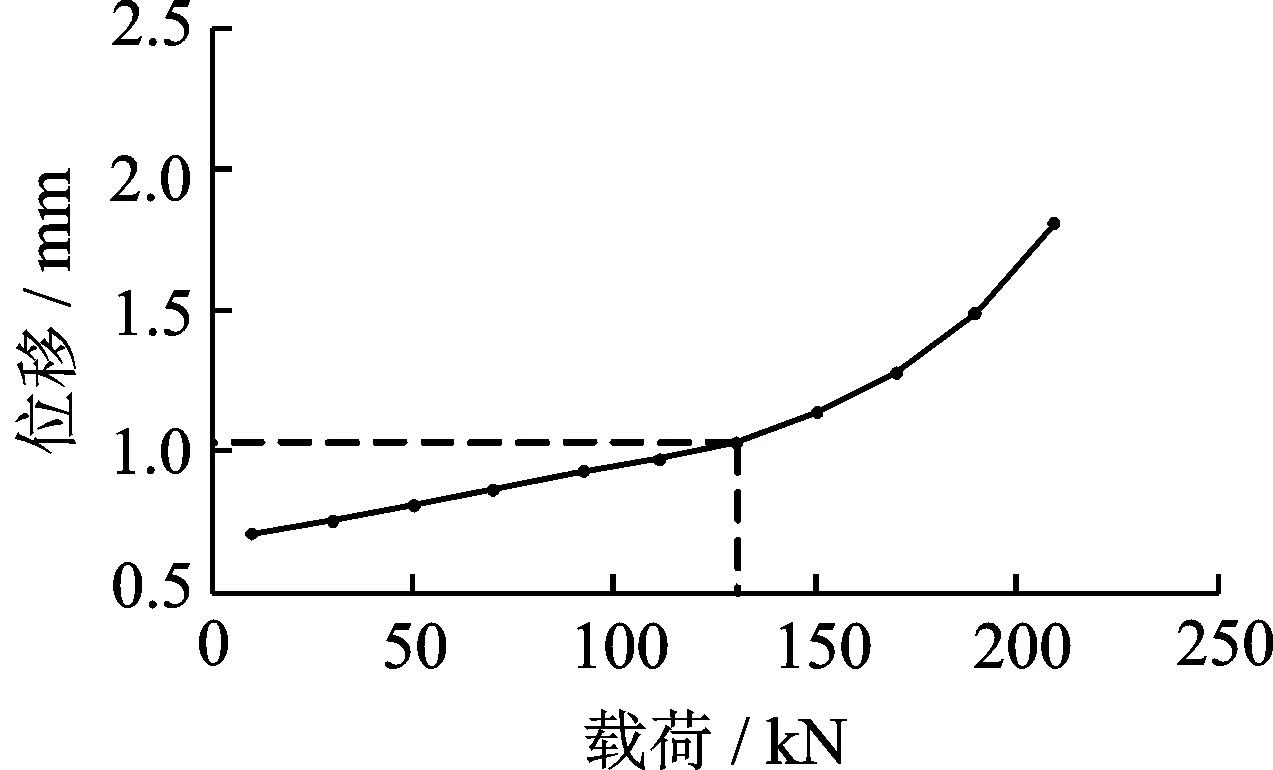
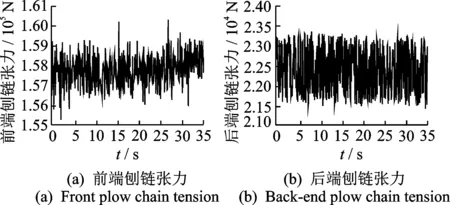
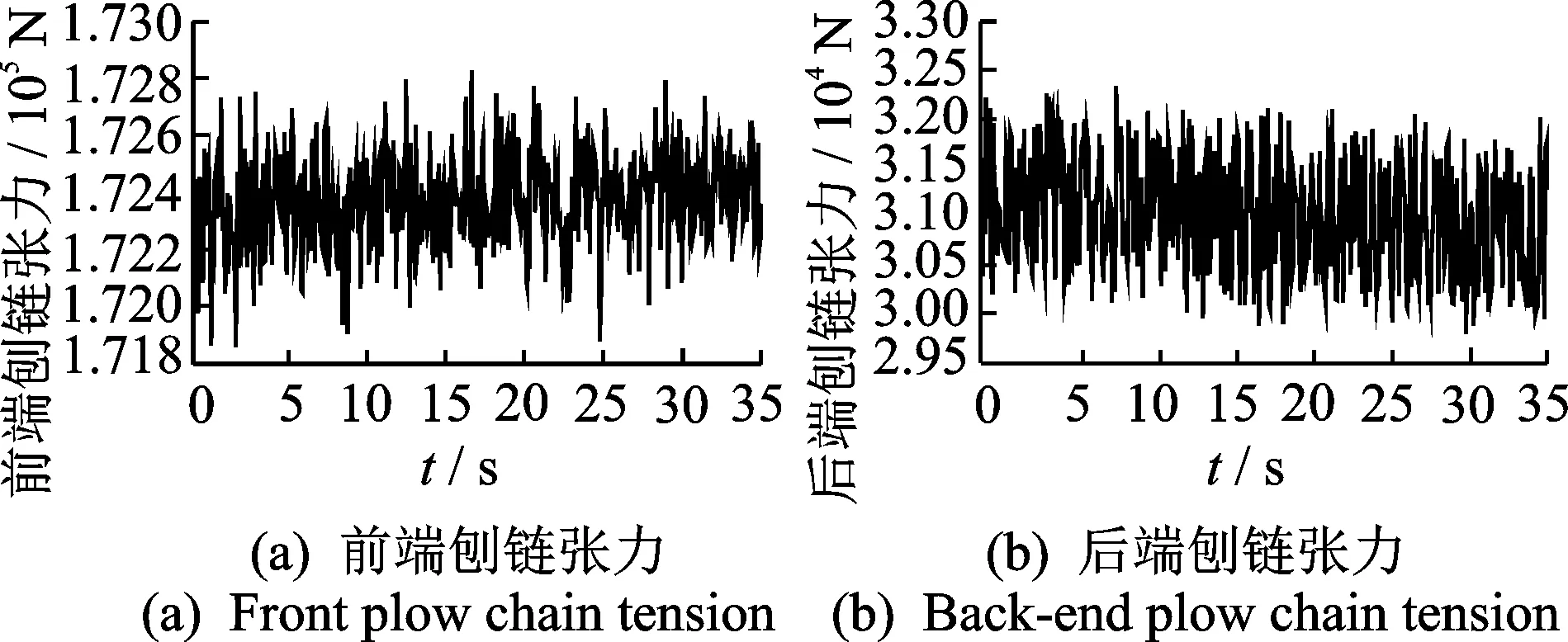
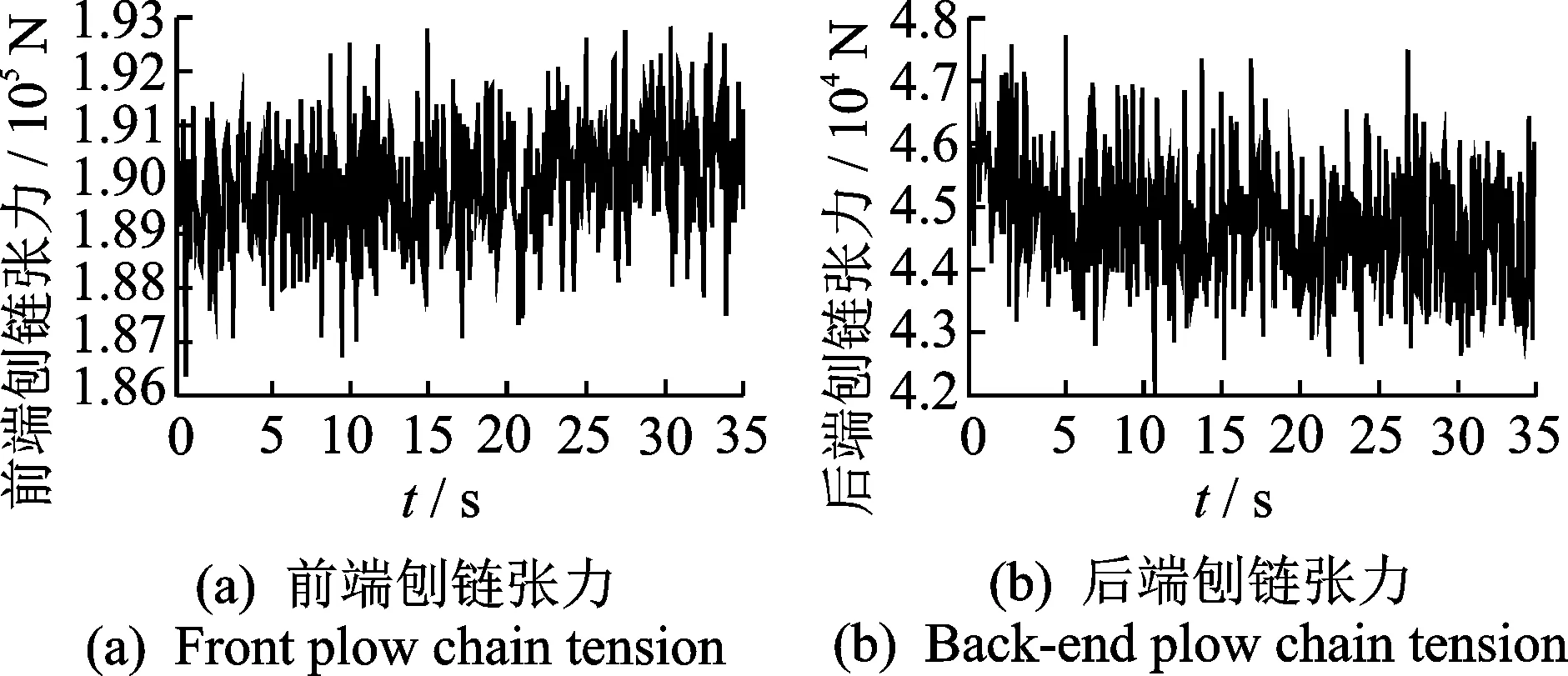
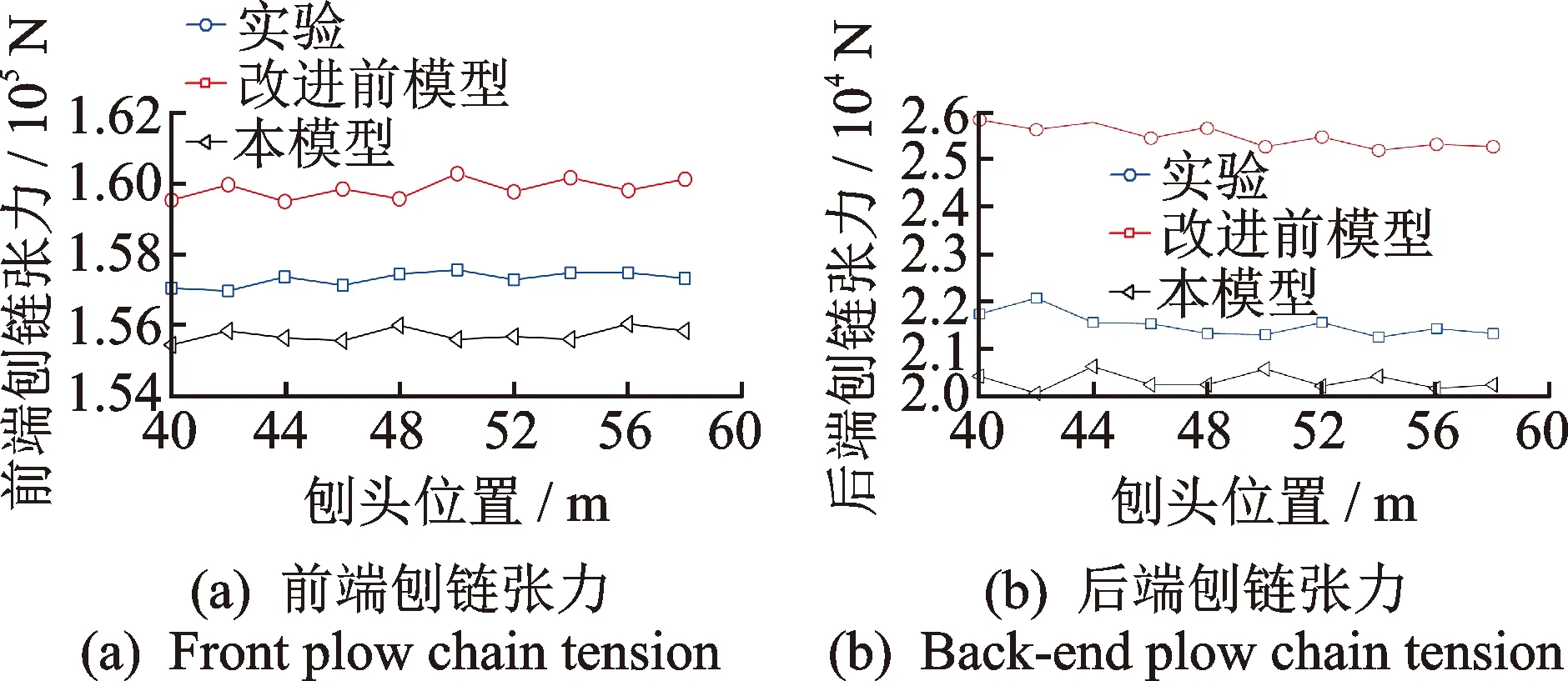
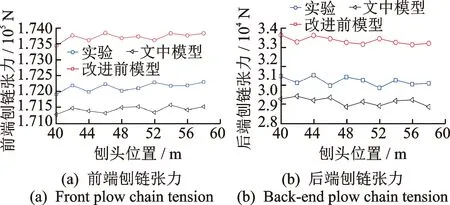
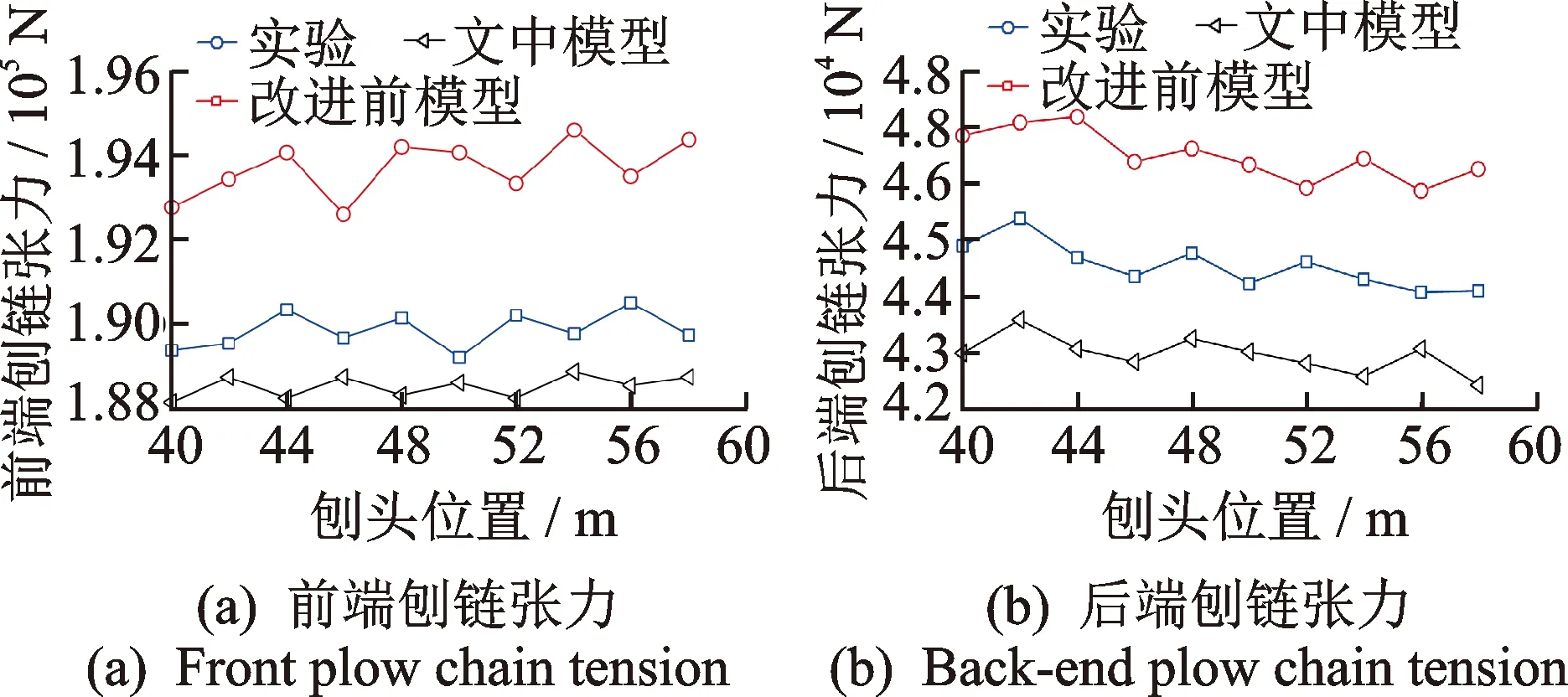
随着刨头连续移动,刨头前后端刨链长度时刻变化,驱动链轮II紧边处、驱动链轮I松边处的刨链质量、刚度为变量。令每个质量单元的有效长度为l,以x=l/2为基准,当刨头移动位移大于l/2时,将驱动链轮II紧边处所移动的刨链质量等效到驱动链轮I松边处,剩余部分平分给下一质量单元及驱动链轮II上,当刨头运动范围在0 图3 当0 (0 (2) 文中采用符号函数表示如下 Fr为刨链剩余预紧力(N)表示为 其中:Fv为刨链初始预紧力(N);g为重力加速度(m/s2);t为系统运行时间(s)。 其中:Z为驱动链轮的齿数;φ0为链轮初始转角;Fμ1,…,Fμ 9为刨链与链道之间的摩擦力(N)。 (l/2 (3) 图4 当l/2 图5 当l≤x3≤3l/2时有限元动力学模型Fig. 5 Finite element dynamic model when l≤x3≤3l/2 (4) 图6 当3l/2≤x3≤2l时有限元动力学模型Fig.6 Finite element dynamic model when 3l/2≤x3≤2l (5) 由文献[13]可知,刨头与滑架体之间存在间隙碰撞,从而产生切向接触摩擦力,文中采用改进的Coulomb摩擦力模型[14],该模型考虑了动态摩擦因数,其模型表示为 (6) μ为动摩擦因数,表示为 (7) 其中:μd为动摩擦因数;μs为静摩擦因数;Vs为黏滞转化速度;Vd为动静摩擦转化速度;V为相对切向速度。 Fn为刨头与滑架体法向接触碰撞力,通过文献[13]的判断准则进行计算,法向接触碰撞力表示为 (8) 其中:δ为碰撞变形量;K为刚度系数。 K表示为 (9) 其中:Ri,Rj为刨头与滑架体接触半径;σi,σj为刨头、滑架体的材料参数。 σi,σj表示为 (10) 其中:Ei,Ej为刨头与滑架体的弹性模量;νi,νj为刨头与滑架体的泊松比。 式(8)中C为阻尼系数,表示为 C=μ'δn (11) 其中:μ'为阻尼因子。 μ'表示为 (12) 将式(12)代入式(11),可得 (13) 即式(8)接触碰撞力模型表示为 (14) 为研究刨煤机的动态特性,首先确定刨煤机刨刀载荷。张家口“煤矿采掘机械装备研发(实验)中心”。根据刨煤机截割煤岩理论,以相似理论为基础,建立一个与实际煤壁在空间上满足1∶1比例以及物理性能参数与实际煤岩相同的模拟煤壁[15],刨煤机系统为用于煤矿井下截割煤岩的实际结构,型号选用BH38/2×400型作为研究载体,刮板机型号为SGZ1000/1050,整体布局如图7(a)所示,煤壁坚固性系数为f3,模拟煤壁全长为70 m,宽度为为2 m,高度为1.5 m。在原刨刀基础上,在刀体上加工方孔,用于安装应变片,并采用带有钩形结构的U形壳体作为保护罩。刨刀测试应变片安装布置及实体图如图7(b),(c)所示。图7(b)中Y为刨刀截割煤壁时的进刀阻力,X为刨刀截割煤壁时的侧向阻力,Z为刨刀截割煤壁时的刨削阻力,应变片2,4测试刨削阻力,应变片3测试挤压力,应变片1测试侧向阻力。测试刨刀在刨头的局部安装位置如图7(d)所示。采用拉力环传感器进行刨链张力测试,采用半桥贴片法,贴片示意图如图8(b)所示,应变片BX120-1BB组成的桥路测拉力环受力大小,拉力环的安装位置如图8(a)所示。通过DH5905Z无线采集模块进行实时数据采集,数据通过无线网络传送到计算机进行存储,并通过DHDAS动态信号分析系统进行数据分析。 图7 实验测试 Fig.7 Experimental test 图8 刨链测试系统Fig.8 Test system of plow chain 本实验对刨头上多把刨刀进行同步实验测试,刨速设定为1 m/s,刨深为10,15和20 mm,文中仅列出单把刨刀的测试结果,截取稳定刨削时的测试结果,时间为30 s,如图9所示,图9(a)~(c)分别为不同刨深对应的刨削阻力曲线。 图9 不同刨深条件下刨削阻力实验曲线Fig.9 Experimental curve of cutting resistance under different plow depth 以BH38/2×400型刨煤机作为分析对象,系统参数如下:刨头质量为3.8×103kg,刨链规格为φ38×137,刨刀与煤壁的摩擦因数为μX=0.3,刨头与滑道的摩擦因数μb=0.2,刨链与链道之间的摩擦因数μ1,…,n=0.25,工作面长度为70 m,驱动链轮齿数为6,链轮节圆半径为R=0.522 m,单位长度刨链的质量为q=29 kg/m,刨链截面积A=2.267×10-3m2;材料参数:Ei=202 GPa,Ej=206 GPa,νi=0.3,νj=0.28,ec=0.9。基于ANSYS有限元软件建立链环与链环接触模型,链条材料为23MnNiCrMo,通过分析得到链条位移云图如图10所示。通过继续施加多组载荷,得到链条载荷-位移曲线如图11所示。刨链刚度系数选取线性段进行计算:k=F/Δl=259 MN/m,由文献[16-17]刚度与阻尼的经验公式可得刨链阻尼系数c=(0.03~0.05)k,则c=1.04×107N·(m/s)-1。 图10 刨链位移云图Fig.10 Displacement cloud of plow chain 图11 刨链的载荷-位移曲线Fig.11 Load-displacement curve of plow chain 将以上得到的刨刀载荷作为外激励施加到刨头上,设定刨头从工作面35 m处进行稳定截割,采用变步长龙哥库塔法求解。通过求解得到不同刨深下刨煤机刨链张力振动曲线,如图12~14所示。其中:图12(a)~图14(a)分别为不同刨深时刨链前端张力;图12(b)~图14(b)分别为不同刨深时刨链后端张力。通过分析可知,在35 s时刻,即刨头运行到70 m处,刨链张力的计算结果未出现计算发散,且刨头前后端刨链张力随着刨深增加,刨链张力值增加,振幅波动更加剧烈,这与文献[8]的研究结果规律一致。 图12 刨深10 mm 时刨链前后端张力Fig.12 Front and rear plow chain tension when plow depth is 10 mm 图13 刨深15 mm时刨链前后端张力Fig.13 Front and rear plow chain tension when plow depth is 15 mm 图14 刨深20 mm 时刨链前后端张力Fig.14 Front and rear plow chain tension when plow depth is 20 mm 图15 刨深10 mm时刨链张力值对比Fig.15 Tension comparison of plow chain when plow depth is 10 mm 图16 刨深15 mm时刨链张力值对比Fig.16 Tension comparison of plow chain when plow depth is 15 mm 将未改进前有限元动力学模型、文中非线性时变动力学模型对应的刨头在不同位置时刨头前后端刨链张力均值与实验测试结果进行了对比分析,选取刨头稳定刨削区间段40~58 m进行研究,间隔2 m计算一组刨头前端、后端的刨链张力均值,如图15(a,b)~图17(a,b)所示。其中:图15(a)~图17(a)分别为不同刨深时刨链前端张力对比图;图15(b)~图17(b)分别为不同刨深时刨链后端张力对比图。通过对比可知,两种动力学模型的计算结果与实验测试结果规律一致,时变动力学模型的计算值相比未改进前有限元动力学模型的计算值更接近实验值,但仍与实验测试值存在误差,且都在10%以内。引起误差的主要原因有:a.计算过程中存在截断误差;b.在求解计算的过程中,刨链各部分之间的刚度值和阻尼值均为近似值,与实验过程中存在着一定的偏差。 图17 刨深20 mm时刨链张力值对比Fig.17 Tension comparison of plow chain when plow depth is 20 mm 以BH38/2×400型刨煤机作为研究对象,基于质量替换法,建立了刨煤机系统时变动力学模型。采用数值分析方法对其在不同刨深条件下的动力学特性进行了求解,得出刨头运行到工作面尾端,刨链张力计算值未出现发散问题,且刨头前后端刨链张力随着刨深增加,刨链张力值增加,振幅波动更加剧烈。将计算结果与改进前动力学模型计算结果及实验测试结果进行了对比,结果规律一致,验证了本方法的有效性及可行性。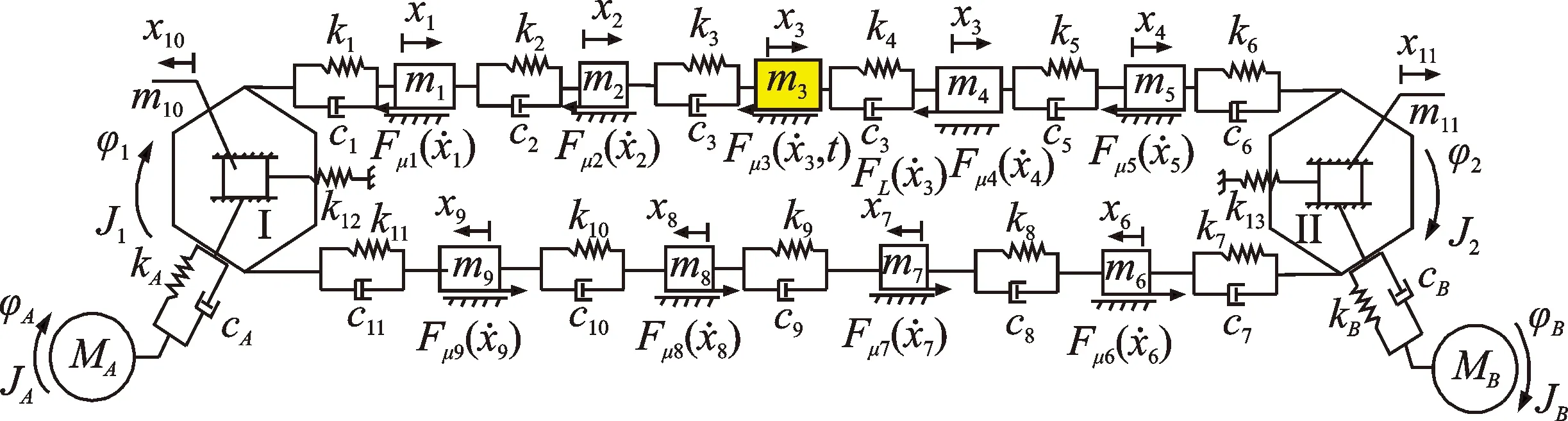
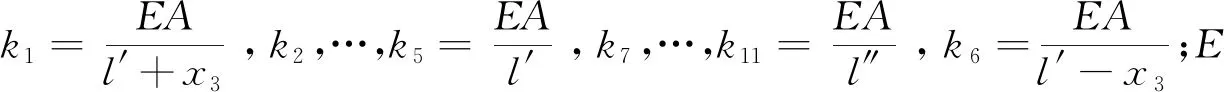
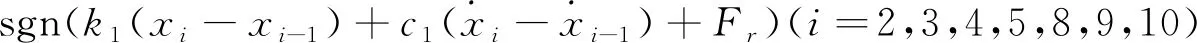
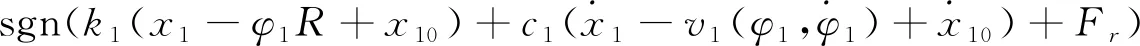

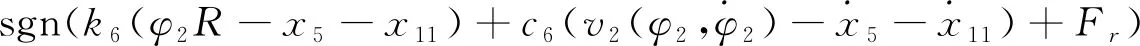

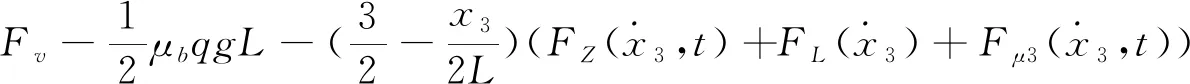
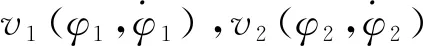



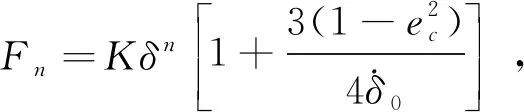

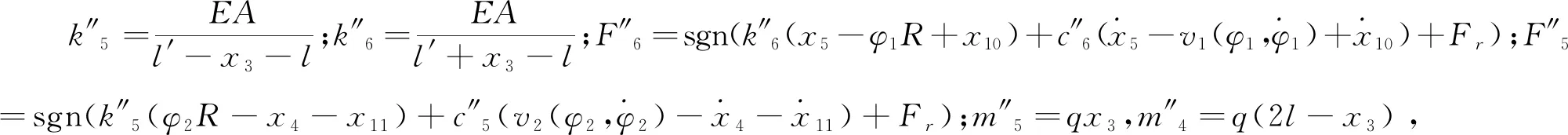
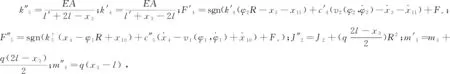
2.2 刨头与滑架体接触碰撞模型

3 刨刀载荷获取

4 数值求解及实验验证
5 结束语

