斜置方柱气动力特性试验研究*

邓然然， 马文勇, 2， 柴晓兵， 郑 熙

(1.石家庄铁道大学土木工程学院 石家庄，050043) (2.河北省风工程和风能利用工程技术创新中心 石家庄，050043)

引 言

方形断面的高耸、细长建筑物及构筑物在强风作用下易产生振动甚至遭到破坏，风荷载常成为其控制荷载。这类结构的风荷载常常被简化为垂直风向下二维方形断面上的气动力[1-5]。然而,实际工程中细长结构轴向往往与来流方向不垂直，例如，倾斜的桥塔、输煤栈桥、建筑物之间的连廊等。

斜向风问题早在1917年就引起了学者的关注[6]，有学者提出可以将风速分解为垂直结构轴向分量和顺结构轴向分量，进一步忽略顺结构轴向分量的影响，流场近似与垂直结构方向分量单独作用下情况一致[7],该方法被称作风速分解法。研究表明，对于椭圆形柱体结构[8]、圆形断面结构[9]、大跨度桥梁主梁[10]以及倒梯形桁梁桥[11]等结构，风速分解法都存在不适用的情况。

与垂直风向下的方柱不同，斜置柱体的绕流形态表现出更强的三维特性，其中沿柱体轴向出现轴向流动是形成这种三维绕流的主要原因之一。一方面，流体会在斜置柱体背风面上下侧交替出现带有轴向速度分量的旋涡，该旋涡会按一定速度沿轴向流动，形成展向旋转流[12]。另一方面，在背风面较强轴向流的出现会干扰旋涡脱落从而影响结构的气动力[13]。由于斜置方柱的绕流特性更复杂，再加上其平均阻力一般比垂直风向下的值小，因此相对于垂直风向下的柱体气动力特性，其气动力特性研究很少，气动力取值及作用机理不清晰，而且斜风向的柱体有可能发生垂直风向下无法出现的振动现象[8]。

笔者通过刚性模型测压风洞试验对不同风偏角下方柱气动力沿周向、轴向的分布规律进行了研究，讨论了风速分解法对斜向风作用下方柱的适用性，分析了风偏角对方柱气动力特性的影响。为斜向风下方柱或者类似断面细长结构的风荷载取值提供了参考。

1 试验概况

试验段宽为4.38 m，高为3 m，长为24 m，在23 m/s风速时试验段中心区域速度场不均匀性小于0.5%，背景湍流度小于0.5%[14]。

方柱模型断面边长B=180 mm，在来流与柱体轴线夹角最小(54°)时柱体最长Ln=3.7 m，在垂直风向下最短L0=2.9 m，以模型的中心O为中心旋转模型来改变风偏角。受试验断面宽度的限制，来流与轴线夹角每改变10°就需要将模型两端对称截掉一定的长度，在此过程中模型垂直于风向投影长度始终为L0。模型由ABS板制作而成，为了增加模型的刚度，在模型的中心位置放置1根长为4 m、直径为50 mm、厚度为5 mm的无缝钢管。为减弱自由端部引起的不利影响且不影响沿轴向的流动，在模型上、下游端部分别安装尺寸为1.2 m×3.6 m和1.2 m×2.4 m的导流板，其中上游导流板封闭，下游导流板设置了直径为700 mm的圆孔，从而确保可能的轴向流动，孔的圆心至端板前缘的距离为1.1 m。当来流垂直于方柱轴向时，下游导流板也封闭。

试验为刚性模型测压风洞试验，测点的布置情况如图 1所示。沿模型展向布置A，B，C，D共4圈测点，其中C圈在模型的中心位置，B圈距C圈650 mm，A圈距C圈1 300 mm，D圈距C圈780 mm，每圈布置44个测压点。考虑到柱体边缘部位风压变化比较剧烈，为能更好地捕捉角点附近位置处风压变化，准确地描述模型截面风压分布情况，每边测点距离角点位置依次为5，15，30，50，70和90 mm。为方便描述风压沿模型轴向的分布，在截面边长的中点沿轴向分别布置E，F，G，H共4排测点，测点间隔为100 mm。

定义来流风速与垂直于模型轴向的分量之间的夹角为风偏角Λ。试验风速为10 m/s，Λ=0°，10°，20°，30°和36°时，基于垂直柱体轴向风速分量计算得到的雷诺数分别为1.24×105，1.22×105，1.17×105，1.08×105和1.01×105。

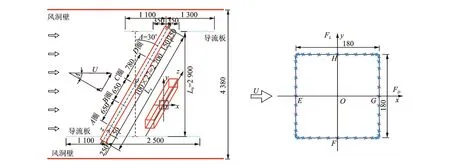
图1 模型及试验参数定义(单位：mm)Fig.1 Test model and definition of testing parameters(unit: mm)

2 试验结果

2.1 垂直风向结果

如表 1所示，垂直风向下4圈测点所在断面上平均阻力系数与其他学者[1-3, 5]的研究成果接近。B，C，D这3个断面受端板影响较小，平均阻力系数基本一致。A断面距离端板比较近(0.8B)，受端板影响较大，断面上的阻力比其他断面大。

图2为风偏角Λ=0°(即来流垂直结构轴向)时模型4个截面上平均风压分布与已有研究结果的对比[1-5]，图中横坐标x/B为测点距左下角角点距离与模型边长的比值，为无量纲量。由图 2可以看出，试验中4圈测点的平均风压系数与已有结果吻合良好，说明研究的试验方法可靠。由于方形模型角点分离气流的流动状态受试验条件的影响较大，因此图 2中各个学者所得的平均风压系数在侧面及背风面上离散程度比迎风面大。本研究试验条件与文献[3]中的试验条件接近，试验结果也更接近。在迎风面角点处部分测点出现了负压，在背风面上A圈测点的负压比其他3圈的负压要小很多，这种差别可能是由于A圈测点距离端板较近(0.8B)、受端板的影响较大引起的，其他3圈的一致性说明端板对其影响很小。

表1 本研究结果与其他文献比较

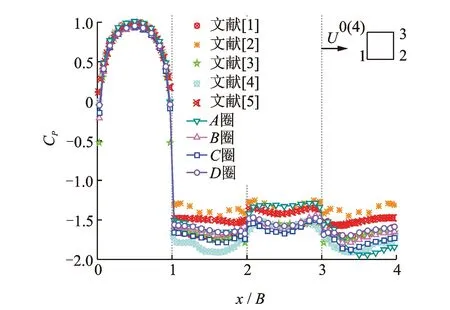
图2 平均风压系数Fig.2 Mean wind pressure coefficients

与平均风压分布类似，脉动风压分布(见图3)也与已有的研究成果分布一致。相比而言，无论是与已有的研究成果还是不同测试断面之间的脉动风压，迎风向取值表现出更好的一致性。本研究中4圈测点的平均风压系数、脉动风压对称性良好；B，C，D圈的吻合及模型对称性良好，来流均匀。从图中可以看出，模型中部背面和侧面的脉动风压更强一些，4个断面在侧面后缘角点处脉动值发生小幅度的剧烈变化。因为在此处受结构外形的影响，流体流动状态发生转变，因此脉动风压系数较大，这种剧烈变化跟测点的位置有关。与其他研究成果相比，本研究试验边缘测点更接近柱体边缘，因此脉动风压更强。

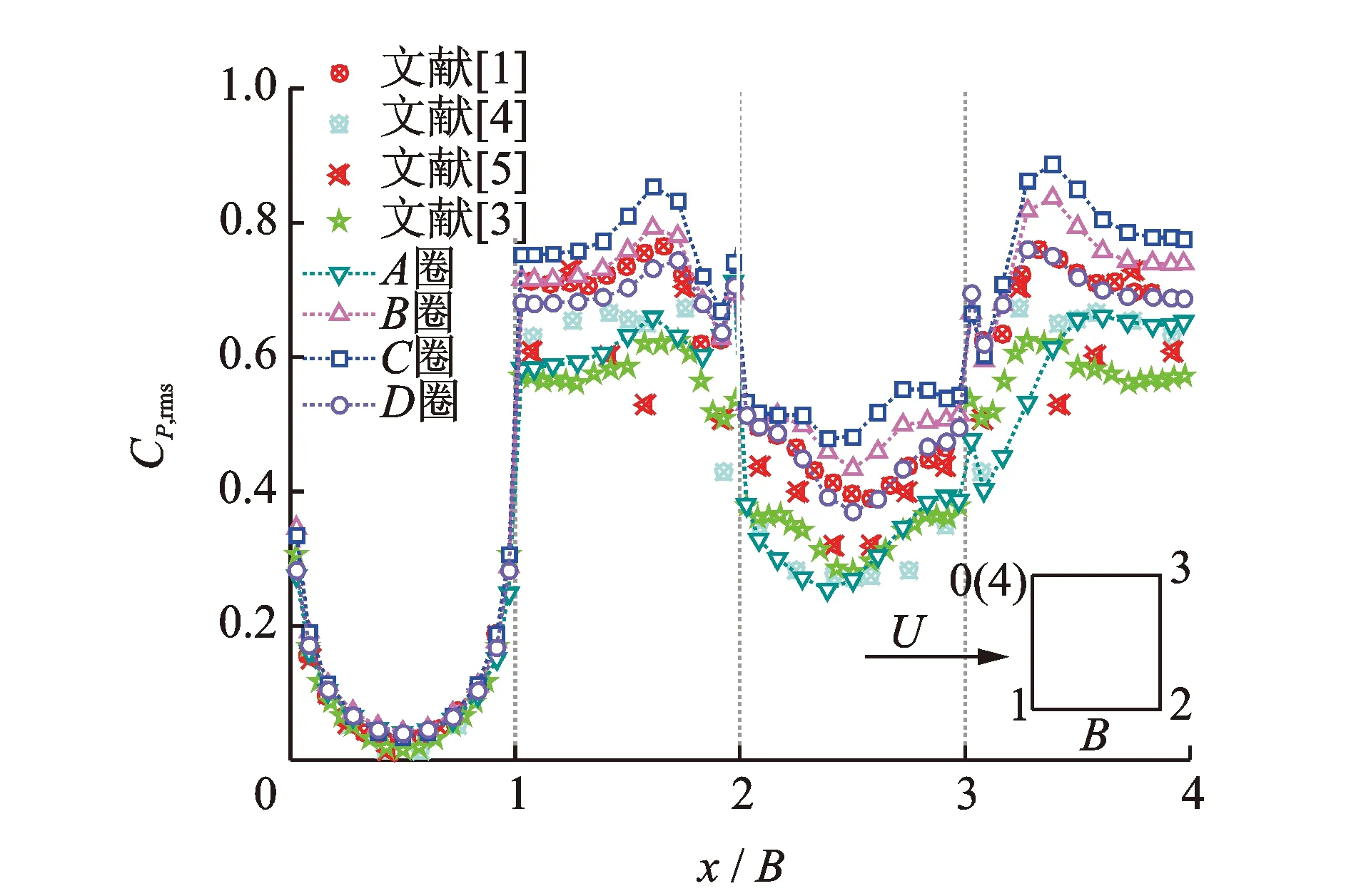
图3 脉动风压系数Fig.3 Standard deviation of wind pressure coefficients

2.2 斜风向速度分解法的适用性

根据风速分解法，来流方向与模型轴向不垂直时，将来流按照矢量分解法分解为垂直轴向以及平行于轴向的分量，采用垂直于轴向的风速分量来代替来流风速计算风压系数，如式(1)所示

(1)

其中：i为测点编号；P(i)为测点处风压；P0为静压；U为来流风速；ρ为空气密度；Λ为风偏角；CPi为i点的风压系数。

笔者用符号CP和CP, rms表示风压系数的平均值和标准差，分别称为平均风压系数和脉动风压系数。

从数学定义上看，当Λ=0°时，cosΛ=1，该式与传统的风压系数定义一致。当Λ=90°时，cosΛ=0，因此无法处理Λ≈90°时的斜风向问题。为了讨论风速分解法的适用性，图 4给出了C断面Λ=0°～36°时基于垂直轴向风速分量计算所得平均风压沿周向的分布情况。若风速分解法适用，那么各个工况下的CPn应该相等。

图 4中斜向风下C断面迎风面风压基本重合，而侧面及背风面上的平均风压系数取值相差较大，分布规律也不相同，因此斜置方形断面结构中风速分解法对于分离点之前的正压范围内适用，对于分离点后表面风压的分布并不能采用风速分解法估算。

图4 基于垂直风速分量的平均风压系数对比Fig.4 Comparison of mean pressure coefficients based on Un=UcosΛ

2.3 斜置方柱的气动力分布规律

2.3.1 平均气动力系数

来流与结构轴向存在夹角时基于垂直结构轴向风速方柱的平均阻力、升力系数采用式(2)和式(3)计算

(2)

(3)

其中：θi为测点与模型中心O点之间的连线与来流反向之间的夹角；di为测点对应的计算长度。

作用在柱体上的平均气动力系数随风偏角的变化规律如图 5所示。斜向风作用下4个断面的平均升力系数重合性良好，取值均在0附近，说明斜风向下柱体两侧的流动仍然保持对称状态。

由图5可以看出，不同风偏角下计算得到的阻力系数有一定的差异，其中以C断面为例，其最大阻力系数为2.17，最小阻力系数为1.69，两者相差28.4%。斜风向下不同截面位置的阻力系数也表现出了一定的差异，这可能是由斜风向下的三维流动特性引起的。

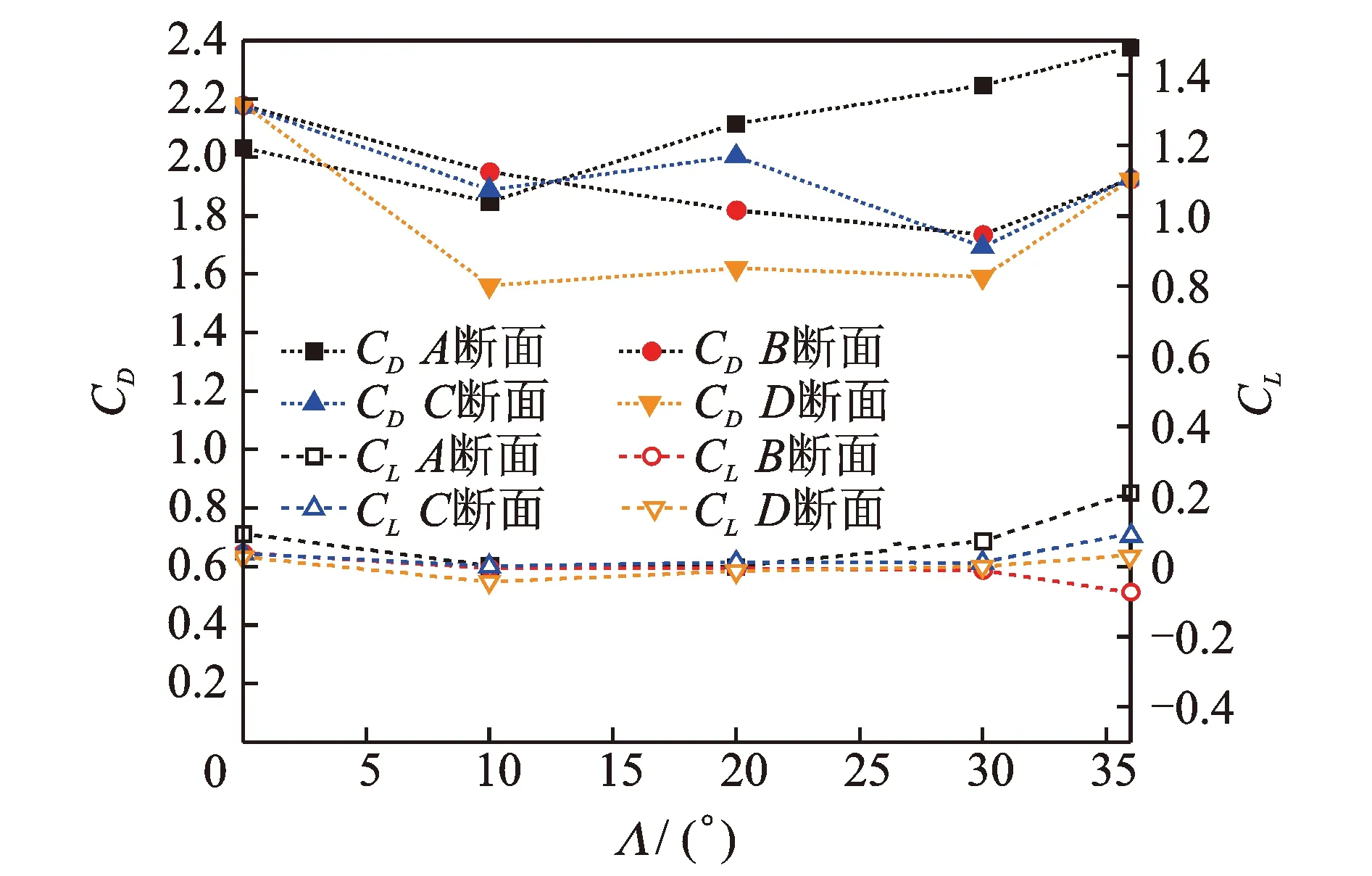
图5 阻力和升力系数随风偏角的变化Fig.5 Variation of drag and lift coefficients with skew angles

2.3.2 风压沿轴向分布规律

由阻力系数的定义可知，作用在模型上的阻力是由迎风面、背风面风压决定的，而当Λ=0°～36°时迎风面平均风压系数基本一致，因此阻力系数的差异主要是由背风面风压的差别引起的。图 6给出了Λ=0°～36°范围内背风面中点沿轴向的风压分布规律，图中横坐标为测点距模型中心距离z与Λ=36°时模型轴向长度Ln的比值，为无量纲量。垂直风向下平均风压系数(图 6(a))沿轴向分布较均匀，脉动风压系数(图 6(b))沿轴向分布并不均匀。由此可见，垂直风向下模型周围流场也并非理想的二维流动。

由图6可以看出，斜向风作用下背风面的负压绝对值及脉动风压均比垂直风向下小。随风偏角的增大，气体轴向流动变强，流体流动状态更加复杂，脉动风压系数最大值变小，背风面负压绝对值变小。Λ=10°，20°时背风面中点处自上游到下游负压绝对值先增大后减小，分别在B，C断面处最大。与平均风压相对应，脉动风压系数也是先增大后减小，在相同位置取得最大值。Λ=30°，36°时在B断面至D断面范围内背风面中段的平均风压沿轴向变化较小，脉动风压系数比小偏角时小且沿轴向分布较均匀。B，C，D断面处阻力系数吻合良好，与图 5中规律一致。

为更好地了解结构整体的风压分布，图 7给出了方形模型侧面风压沿轴向的规律。由图可以看出，模型上下表面风压吻合良好，侧面以及背风面风压表现趋势一致，从上游到下游负压逐渐减弱。侧面负压比背面负压强，此差别自上游至下游逐渐减弱。在距上游端板一定距离时，侧面及背风面之差在此点之后的范围内均小于10%，处于同一尾流区域内。

由风压沿轴向分布规律可知，在Λ=10°～36°范围内流体流经斜置柱体时表现出复杂的三维流动特性，这种三维流动主要体现在侧风面和背风面。

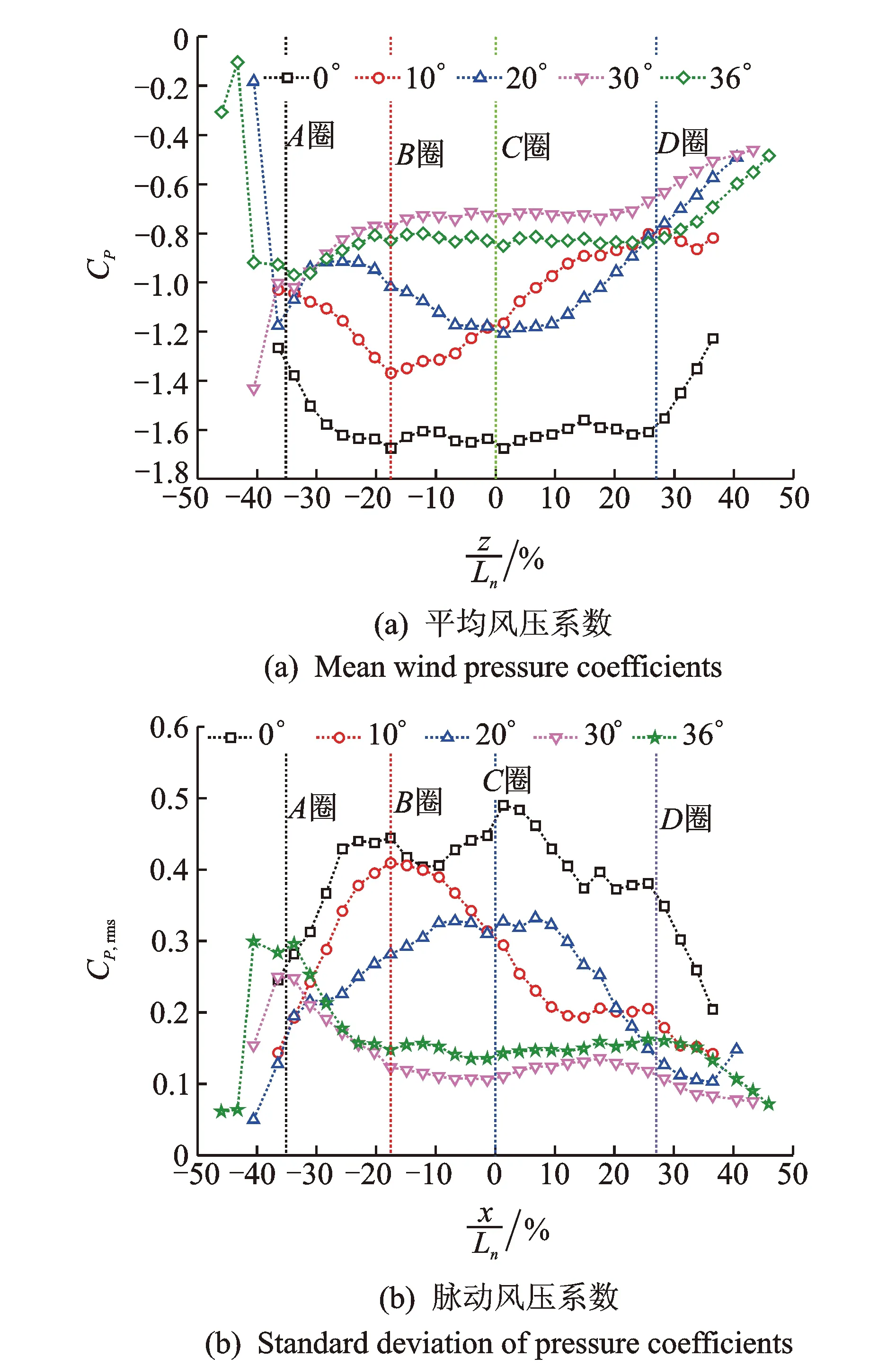
图 6 模型背风面中点的风压系数Fig.6 Variation of the base pressure coefficients

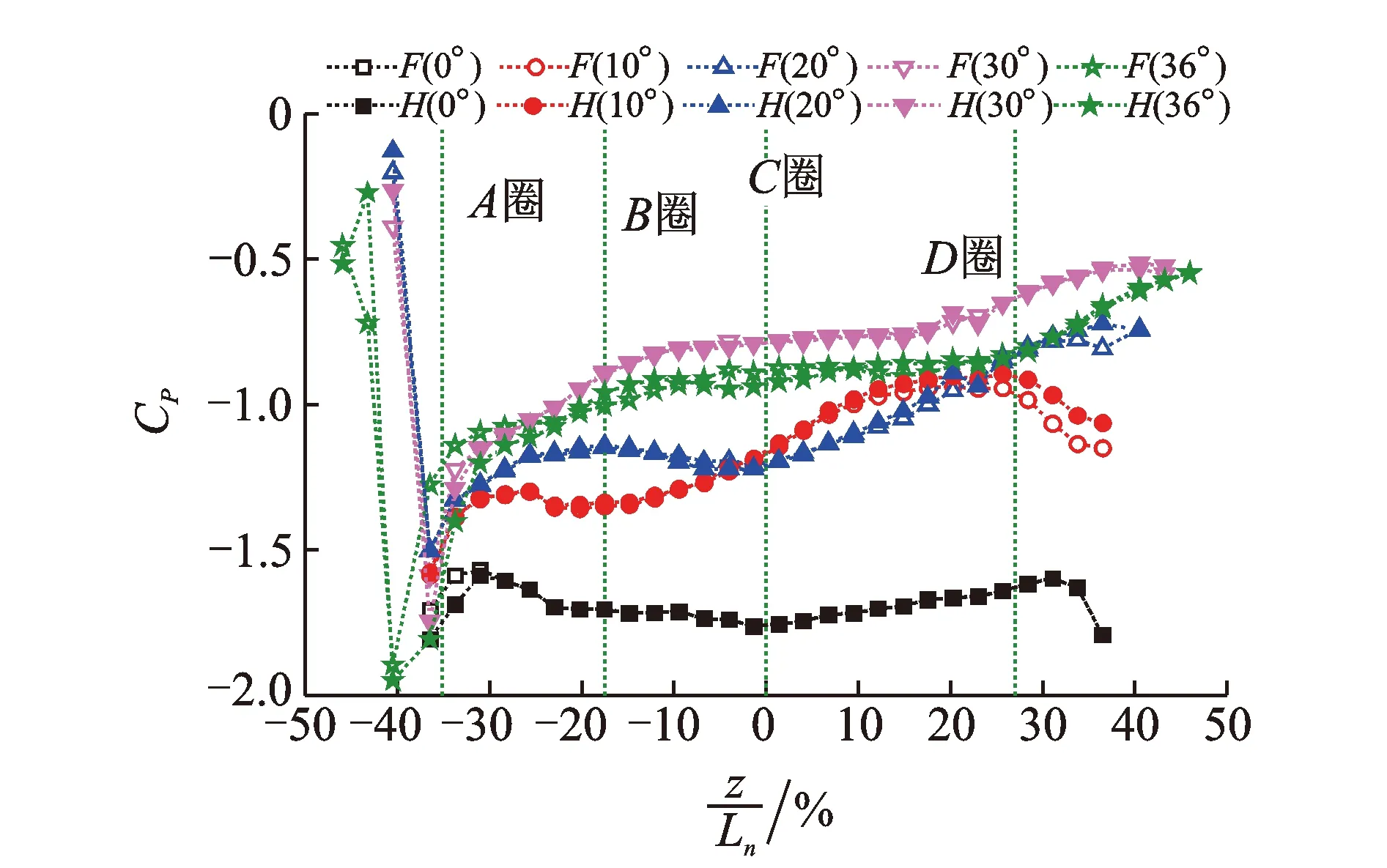
图 7 模型侧风面中点的风压系数Fig.7 Variation of the lateral pressure coefficients

从以上讨论可以看出，当来流与柱体轴向不垂直时，平均风压系数和脉动风压系数沿轴向变化很明显。这种变化的原因有：a.无论从平均还是脉动气动力的角度看，轴向流的产生使得斜置方柱的绕流变成三维绕流，这种三维绕流本身使气动力沿轴向呈现非均匀分布；b.风洞试验中柱体上游端部会产生端部绕流(尽管在试验中采用导流板减弱了这种绕流效应，但是很难完全消除)，这种绕流会随着轴向流沿柱体轴向向下游输运，也会对气动力沿轴向的分布产生一定的影响，其影响范围可能与斜置圆柱的偏角有关。

2.3.3 周向风压分布规律

为进一步了解模型表面的流动状态，分析了各个断面上风压分布情况。因为在Λ=0°～36°范围内A断面受端板(Λ=36°时距端板约为2B)影响较大，此处不讨论。图 8为Λ=0°～36°范围内方形断面模型各圈测点平均风压沿周向的分布规律，由图可以看出，斜向风作用下侧面及背风面风压与垂直风向下相差较大，侧面风压自上游至下游逐渐减弱，并更接近对应的背风面风压。这种变化规律说明，随着流动向下游的发展，侧面和背面的风压差别越来越小，3个面均位于上游分离流的尾流中，因此其风压分布反映的是该位置上游流动尾流对该区域的影响，而不是该位置迎风面的分离流对其的影响。这也说明，不能将倾斜的方柱等效为二维矩形断面。

不同斜风向下背风面风压的分布规律也不同。以C断面为例，风偏角较小时(0°，10°和20°)背风面中间风压强而两侧风压弱；风偏角较大时(30°和36°)中间风压弱而两侧风压强。背风面风压分布规律的变化反映出了尾流随风偏角的变化，当风偏角较大时，背风面的轴向流较强，因此对应的背风面中心位置的负压比两边强；而当风偏角小时，背风面边缘处流体由于再分离产生的风压更强，因此背风面中心位置的压力相对较弱。

斜向风作用下负压最强的位置在后缘角点处。B和D断面10°≤Λ≤30°范围内随风偏角的增大气流流经方柱时逐渐变缓和，侧面、背面负压逐渐减弱。

各个风偏角下迎风面上风压系数脉动值基本一致(见图 9)。侧面脉动风压系数在Λ=0°时比较大，其取值范围为0.6～0.8。斜向风作用下脉动值均比垂直风向下小，风压系数的波动较小。随风偏角的增加脉动风压系数呈减小的趋势，两侧脉动风压系数要比模型中部小，在侧面后缘角点处脉动值略有增加。Λ≥30°时侧面以及背风面上脉动风压系数均在0.15左右，在C圈处出现Λ=20°时脉动风压系数比Λ=10°时稍大的情况。

2.3.4 风偏角对旋涡脱落频率的影响

图 10给出了不同风偏角下各个断面的升力系数幅值谱(SP)，定义斯托罗哈数St=fsB/(UcosΛ)，其中fs为升力系数幅值谱的卓越频率。

由图 10可以看出，风偏角对方柱旋涡脱落的频率和强度都有影响，其体现在斯托罗哈数的数值、峰值大小以及频率带宽上。总的来说：随着风偏角的增大，斯托罗哈数变小，旋涡脱落频率变小，其对应的尾流变宽；能量的集中程度也在变弱，表现为特征频率的带宽变宽，这说明随着风偏角的增大，尾流的规则旋涡脱落受到了轴向流的干扰，旋涡破碎；结合图9中背风向脉动风压系数随风偏角的增大而减小可知，破碎后的旋涡会降低脉动风压的强度。

Λ=10°时B断面旋涡脱落强度最大；Λ=20°时则是C断面最大；Λ=30°时D断面旋涡脱落频率较明显，能量也比较集中；Λ=36°时虽然旋涡脱落不明显，但是D断面能量要比其他断面强。由此看来，随着风偏角的增大，旋涡能量集中的位置逐渐向下游移动，这与风压沿轴向的分布规律一致。这可能是由于风偏角越大沿结构轴向的流动随之增强，削弱了展向涡引起的，这也是结构风压沿轴向变化的主要原因。

由图10可以看出，随着风偏角的增大，旋涡脱落频率减小，频带增宽，强度减弱。这种变化会对结构的涡激共振发生的风速产生明显的影响，因此需要在抗风设计中引起重视。

图8 方柱模型的平均风压分布Fig.8 Mean wind pressure distributions around square prisms

图9 方柱模型的脉动风压分布Fig.9 Standard deviation of wind pressure distributions around square prisms

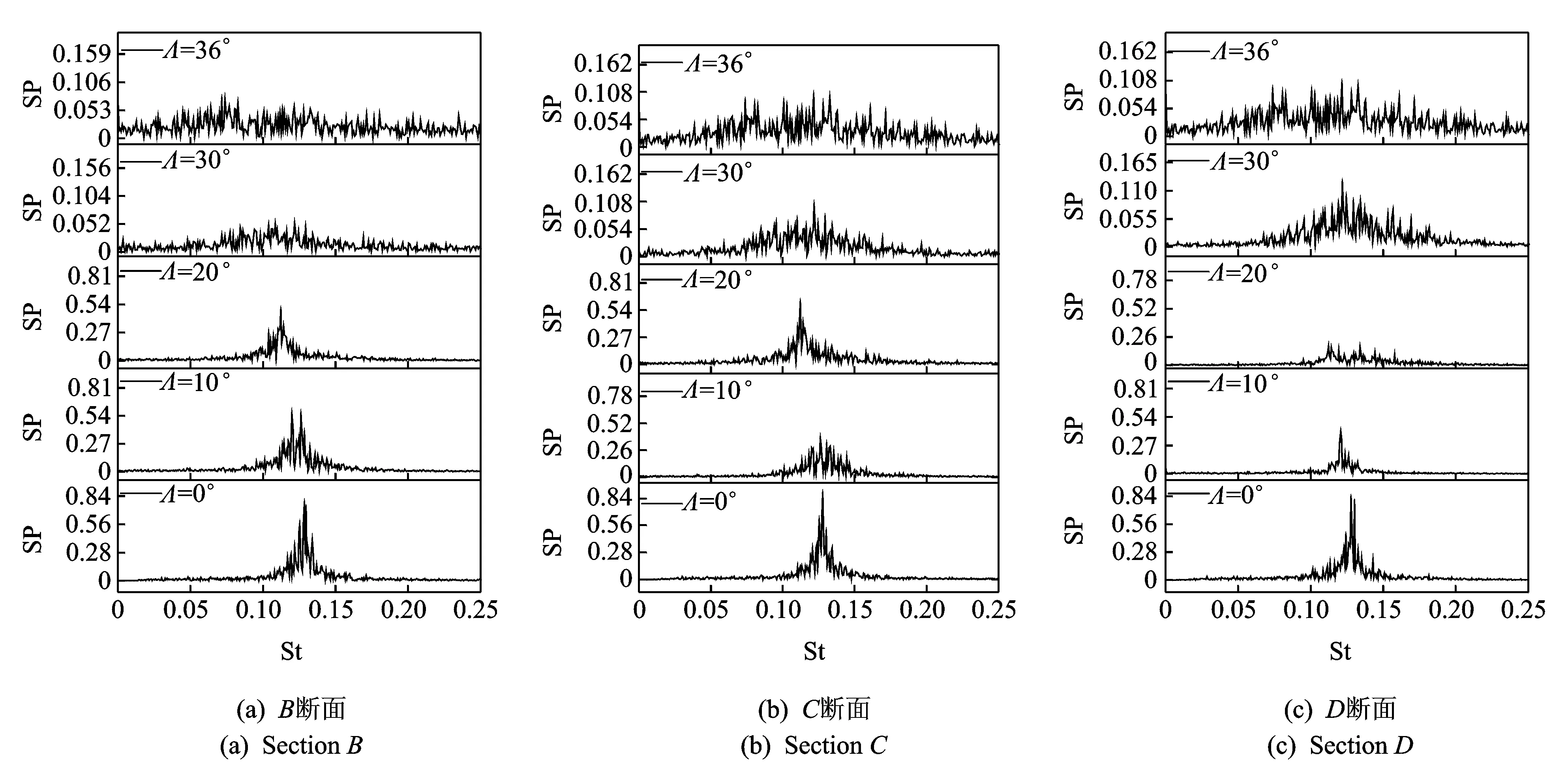
图10 4个风偏角下升力系数幅值谱Fig.10 Amplitude spectrum of lift coefficient for four skew angles

3 结 论

1) 方形断面结构在斜向风作用下风速分解法对于驻点到分离点之间的正压区域适用，而对于分离点后的负压并不适用，因此不能用传统风速分解法估计斜向风作用下方柱的整体气动力。

2) 范围内迎风面风压分布一致，斜向风作用下侧面及背风面负压的绝对值在后缘角点处最大，但比垂直风向下小，因此斜风向下的平均气动力小于垂直风向下的气动力值。从平均力的角度看，采用垂直风向下的气动力对结构进行抗风设计是偏于保守的。

3) 斜向风作用下旋涡脱落频率减小，强度减弱，带宽增大。这种变化会降低方柱涡激共振的起振风速，也可能增大其锁定区间，需要在抗风设计中引起重视。由于旋涡脱落强度的减弱，其涡激共振的响应会有所降低。