从“数”“怎么数”到“不数”——“平行四边形的面积”教学实践

朱孟迪

一、“数”还是“不数”

学习“平行四边形的面积”之前，我们进行了前测：给定一个平行四边形（底6cm，高4cm，邻边5cm）,让学生想办法得到这个平行四边形的面积，结果如下：

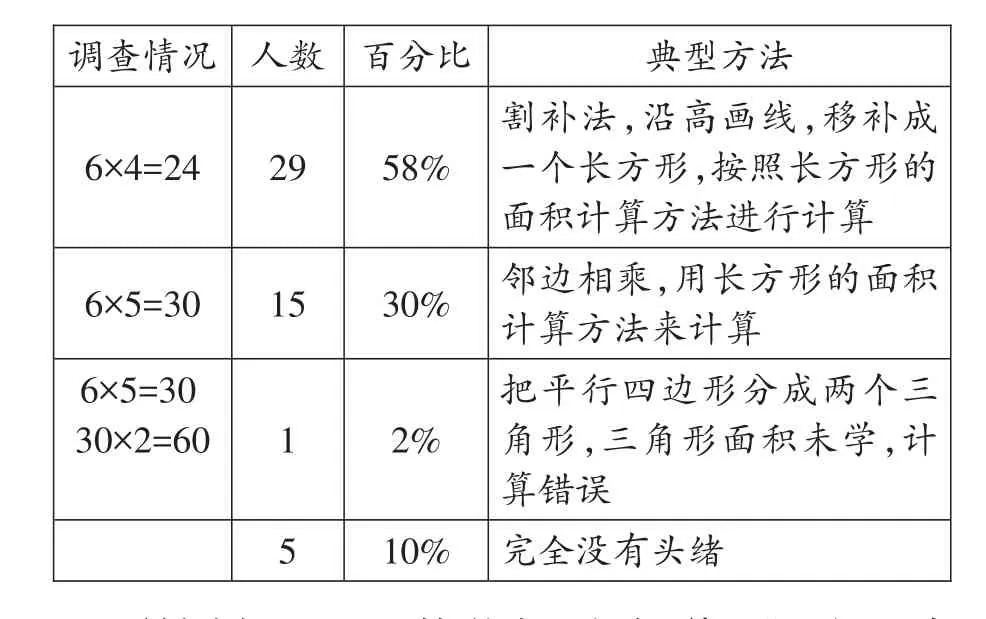
调查情况6×4=24 6×5=30 6×5=30 30×2=60人数29 15 1 5百分比58%30%2%10%典型方法割补法，沿高画线，移补成一个长方形，按照长方形的面积计算方法进行计算邻边相乘，用长方形的面积计算方法来计算把平行四边形分成两个三角形，三角形面积未学，计算错误完全没有头绪

前测表明，58%的学生已经知道了“平行四边形的面积是底乘高”，在追问“为什么是底乘高”的道理时，50%的学生已然能用“拼剪成长方形”加以思考。这让我们聚焦这样一个核心问题：平行四边形面积的教学要不要进行“数”单位面积的活动？为什么？

支持“数”的教师认为：（1）教材中安排了“数”单位面积；（2）“数”是求一个平面图形面积的基本方法；（3）虽然有一半多的学生已经知道平行四边形面积的探索，但还有一半左右的学生不明就理，需要利用课堂活动习得。

支持“不数”的教师认为：（1）本课的重点并非“数”单位面积，而是“转化”，因此要把更多的时间集中在“转化”上；（2）前测数据表明，学生有足够的经验自主习得平行四边形的面积了，再回到“数”，是舍本逐末。（3）基于学情，如果学生想到了“数”就呈现，如果学生没有想到“数”就不呈现。

二、“怎么数”

（一）“怎么数”单位面积

贴合学情，找准起点，我们发现学生在三年级下学期已经充分积累了“整格”单位面积“数”的经验，能借助数单位面积探索长方形的面积公式；根据长和宽边上的单位面积的数量推算长方形的面积（包括变式），甚至对半格的单位面积数法也已涉及（见图1）。

图1

学生会如何去“数”平行四边形的面积呢？

（1）先整再零。先数“整格”的单位面积，再数“不满整格”的，把不满整格的当作半格来数。20个整格，8个半格，共24平方厘米（见图2，下同）。

（2）移成整格。将不满整格的“小三角形”想象平移（或旋转），变成整格再数，每行都是6个面积单位，有4行（或上面两行各5个单位面积，下面两行各7个单位面积），共24平方厘米。

（3）移成长方形。将一部分三角形（或梯形）想象着平移，变成长为6厘米、宽为4厘米的一个长方形，得到面积为24平方厘米。

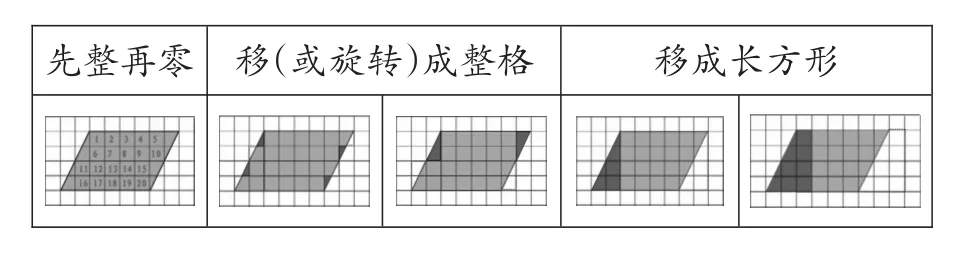
图2

（二）“怎么数”的思维意蕴

在用数单位面积解决平行四边形面积这个新问题的时候，学生要聚焦一个核心问题——不满整格的该怎么“数”。我们分析第一种数法是承接源经验，紧紧依托“整格”单位面积“数”的经验，并将“不满整格的按半格来数”；第二种数法是承接过程经验，借助“平移或旋转”的经验，将“不满整格的”变换成整格的来解决；第三种数法是将经验上升为想象，通过想象平移，将平行四边形转化成长方形来解决。经统计，我们发现学生较喜欢后两种方法，尤其是转化成长方形，深入人心。

学生为什么喜欢后两种方法？主要原因有二：一是转化思想的前经验与潜能力。皮亚杰说过，7岁儿童就已经具备了面积守恒观念。在教学中，学生已经多次接触类似的经验（见图3）。二是思维发展的必然。小学生逐步从“具体形象”思维逐步向“抽象逻辑”思维发展，他们更乐于用“优化”来思维。与一个一个地数相比，整体平移变成长方形更容易数。在“数”的过程中，有新的方法出现，最终走向“不数”。

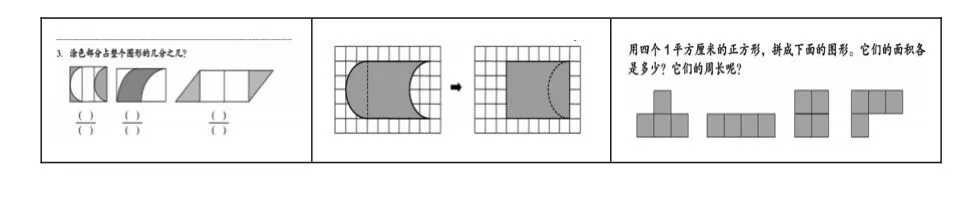
图3

三、“不数”

（一）“不数”是目的

不数，是基于建立“面积计算”的模型。在长方形面积计算公式的探索中，学生借助“数单位面积”，通过若干个不同的长方形，利用不完全归纳法发现长方形的面积可以用“乘法”进行计算，进而得到面积计算公式。在这个过程中，数单位面积的意义就在于从“数”走向“不数”。

本课的一个重要的过程性目标，就是让学生体会到平行四边形可以通过图形转化得到其面积计算公式，其中平行四边形的“数”与长方形的“数”异曲同工，有助于学生建立平行四边形的面积计算模型。而且使学生明白，只要能将未知面积计算公式的图形转化成已知面积计算公式的图形，就能求出其面积。如此一来，为今后求三角形、梯形等图形的面积提供了策略与方法。

（二）“怎么数”是“数”与“不数”的桥梁

综上分析可知，本课的教学要沟通“数”与“不数”。数，只是一个引子；不数，才是最终目的。“数单位面积”对于平行四边形的面积来讲，已经不再是重要经验了。本课的“数”是要在“怎么数”中升华出“转化”的思想，是转化思想的“元认知”。

基于以上的认识，我们进行了教学实践。

四、教学实践——从“数”向“不数”的跨越

教学，需要准确掌握知识的“逻辑起点”和学生的“现实起点”，优化学生的“学习之路”，最终达到高效课堂的目的。

（一）基于学情，引发“数”的需要

前测表明，学生对平行四边形的面积已经有了一定的认知经验。无论是学生头脑中“数”的经验，还是“转化”的经验，都是非常重要的资源。为了与学生的“元经验”接轨，我们让“数”自然显现。

【片段一】

师：今天我们要研究平行四边形，确定这个平行四边形的面积，你想知道什么信息？（出示一个无数据的平行四边形）

生：我想知道它的底和高。

生：我想知道每条边的长度。

师：好吧。（出示数据，见图4）现在你知道它的面积是多少吗？

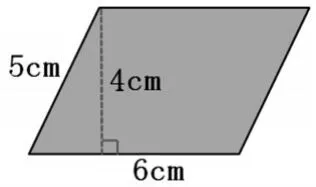
图4

生：24平方厘米。

生：30平方厘米。

师：有同学猜测是24平方厘米，也有同学猜测是30平方厘米。到底是多少呢？让我们一起来研究研究。请你静静地想一想，确定一个平面图形的面积，我们以前有过这样的经验吗？你想到了什么？

生：我们以前学习长方形的时候用到了数格子的方法。

师：是的，那么这个平行四边形是不是也可以用数格子的方法来确定面积呢？

生：可以。

教学中，教师充分调动学生的现有起点和心理需求，引导学生先猜测后验证。面对一个新图形，教师引导学生运用以前学习长方形面积的经验，“数单位面积”自然浮出水面。

（二）贴合学情，探究“怎么数”

【片段二】

师：下面，让我们来听听同学们的想法。

生：我是先数整格的，再数半格的，最后加起来，是24平方厘米。

生：我是把平行四边形的这个部分割下来，然后填补到这里，就变成了一个长方形，长方形的面积就是长×宽。

师：同学们请看，跟长方形相比，“数”平行四边形面积的困难是什么？

生：有半格。

师：以前，我们是没有这个经验的，今天，我们是怎么解决的？

生：把半格的跟半格的拼起来，变成一格。

生：我们可以一个个去拼，也可以把整部分（用手比画）切下来拼成一个长方形，这样就很容易数出来了。

师：既然如此，数格子帮了我们这么大的忙，那么，用这个方法应该可以快速地说出下面这些平行四边形面积吧（见图5）。来，试试看。

图5

（第3幅学生无法口答）

师：看来，“数格子”并不是万能的。那么，还有别的方法可以得到平行四边形的面积吗？

生：我们可以把左边的小三角形剪下来，拼到右边变成长方形，得到了长方形的面积也就得到了平行四边形的面积。

师：你是怎么想到的？

生：我是通过刚才数格子得到的启发。

数单位面积的方法有局限性，但“数”的经验孕育了“剪拼转化”的方法。至此，学生思维的脉络体现得淋漓尽致。

（三）回顾总结，执果索源

如果从平行四边形的面积公式推导的角度来教学，当然要用到“剪拼法”，但会显得比较突兀，而从学生“面积经验模型”出发，数单位面积起到了承前启后的作用。

【片段三】

遇到一个新问题，学生提出猜想，有人猜可能是6乘5，有人猜可能是6乘4，怎么办呢？我们想到了以前学习长方形面积的经验——数格子。我们尝试了几个平行四边形，借助数格子的方法确实能得到许多平行四边形的面积，但后来出现了这样的一个平行四边形，就数不了。怎么办呢？有学生借助数格子的经验想到了“剪拼法”，平行四边形都可以“转化”成长方形，这样一来，知道了长方形的面积也就知道平行四边形的面积。观察剪拼前后，我们发现——平行四边形的底与长方形的长相等，平行四边形的高与长方形的宽相等，因为长方形的面积是长乘宽，所以平行四边形的面积就是底乘高，以流畅的思维，完成了从“数”向“不数”的跨越（见图6）。

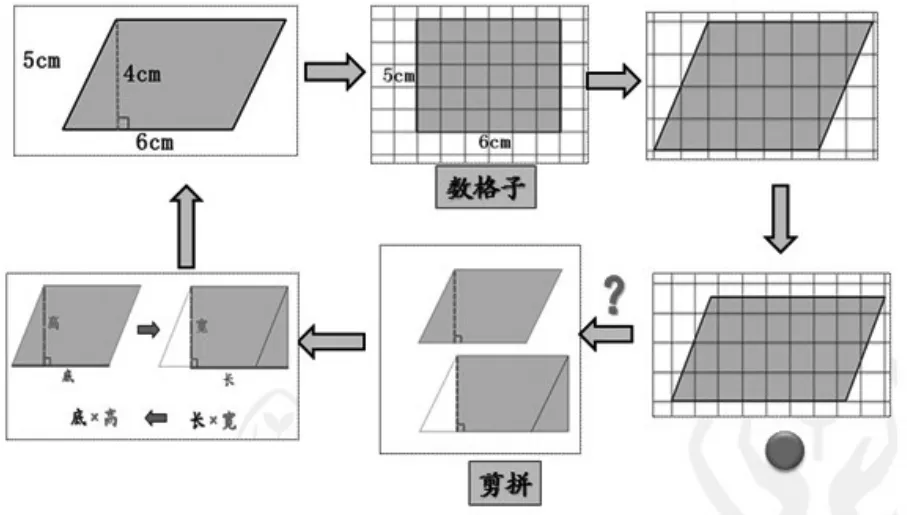
图6

课尾，教师带领学生回望学习历程，建构学习经验框架。在“面积探究”中，由“数单位面积”引发了“剪拼法”的发现，达到了“不数”的目的，体现了数单位面积的价值。

在平行四边形面积的教学中，“数”或“不数”仅仅是一种手段，教师真正应该关注的是其背后的“思维进程”，基于学生“数”的源经验，然后跳出“数”，形成“不数”的新经验（转化）。