一种基于几何统计的卫星移动MIMO信道模型

赵凌开，郭 庆

(哈尔滨工业大学通信技术研究所，黑龙江 哈尔滨150001)

0 引言

经过50余年的发展，卫星通信已成为最先进的通信技术之一，且随着通信技术的不断发展，各个领域的通信需求日益提升。但目前卫星移动通信系统存在卫星轨道位置拥挤、频率资源紧缺的问题，发展形势严峻，因此采用多输入多输出(MIMO)技术手段提高频谱利用率，扩大系统容量成为卫星通信领域的研究热点[1-3]。

本文以卫星移动MIMO信道的衰落特性、统计特性和多普勒频谱为理论基础进行信道建模。对于该问题的研究[4]，在2013年，德国的夫琅禾费海因里希赫兹研究所提出了无线信道模型QuaDRiGa，该模型采用了基于几何学的信道建模方法，实现了任意卫星移动MIMO信道建模[5]；2014年，Mhearáin等人在文献[6]的基础上，通过采用一系列新技术将仿真的采样率提高到了实际传输的数值，提出了双极化卫星移动MIMO信道的增强信道模型[7]。

本文综合统计模型复杂度低和几何模型精确度高的优点，将统计模型与几何模型进行结合，提出了基于几何统计的双极化卫星移动MIMO系统的信道建模理论。该模型总体上使用几何模型的建模思路，采用射线追踪方法对信道中传输的射线进行追踪[8]，在实际计算中引入统计学方法对各种小尺度参数进行建模与处理，同时考虑信道环境造成的信号衰减以及信道环境对射线极化的影响，完成了信道模型的建立。结合仿真验证并与传统模型相比较，分析了模型的正确性及其他性能。

1 理论与方法

本文提出的基于几何统计的双极化卫星移动MIMO系统信道建模理论，技术流程如图1所示。

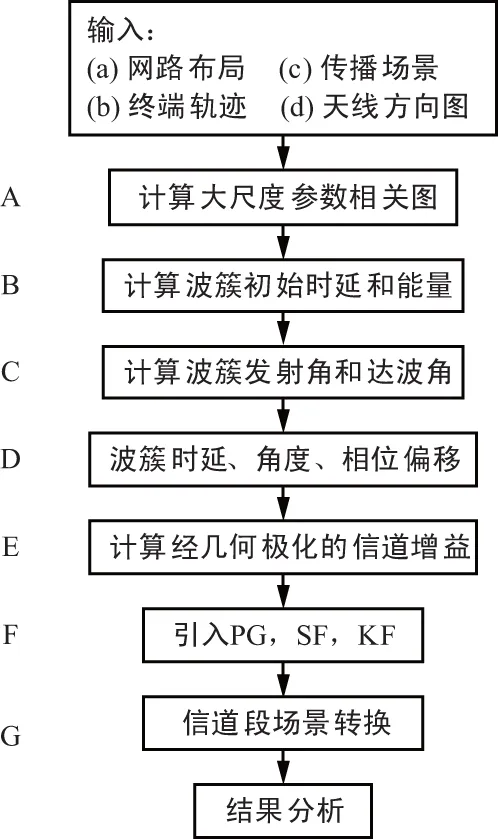
图1 双极化卫星移动MIMO系统信道建模技术流程

该模型实质上是对发射机、接收机和散射体的位置进行几何学定义，再对射线进行追踪和统计学分析而建立起的。建模过程如下：

① 首先输入相关参数，构造整体的通信场景；

② 步骤A对7种大尺度参数在移动终端轨迹上的统计分布进行计算并保存在相关图中；

③ 步骤B,C,D对传播的各条射线进行追踪，持续计算时延、能量、角度和相位并记录；

④ 步骤E,F，先结合收发天线方向图和射线在信道中极化角度的偏转，初步计算信道增益，再根据PG,SF,KF计算较为精确的信道增益；

⑤ 步骤G实现了各段轨迹的衔接与过渡，保证了信道中的增益在空间域和时域的连续性[9]。

1.1 空间域采样

实际应用中，由于每个移动接收端的移动速度不同，采用空间域代替时域采样，更具有普适性。

定义采样密度，为空间域采样率与信号半波长长度之比。只要满足采样密度不小于2即可无失真地还原出信道的冲激响应。

1.2 大尺度参数与相关图的计算

大尺度衰落是信道衰落的主体成分。在双极化卫星移动MIMO信道准确定性模型中，信道特性主要由DS,KF,SF,AsD,AsA,EsD,EsA确定，且信道测量数据表明它们之间存在互相关关系，因此，建模的第一步即是为这7种大尺度参数建立二维相关图，以表征其自相关和互相关特性[10]。

生成相关图的核心思想是通过使用FIR滤波器成功过滤随机的正态分布数列，在固定的采样网格上生成相关图[6]。

1.3 初始时延和功率计算

初始时延由一种场景相关的时延分布计算而来，如式(1)所示：

(1)

式中，Xl～U(0,1)，στ为DS相关图上相应位置的初始时延扩展，rτ为比例因子，作用是表示实际信道中时延τl和功率Pl对στ的影响。

将时延按递增顺序排列并与最小时延作差：

(2)

非直射簇的功率表达式为：

(3)

式中，Zl～N(0,ζ)，ζ为用于仿真波簇在散射体中传输的过程中附加的阴影过程的量。

根据KF相关图可计算直射簇功率：

(4)

(5)

1.4 发射角和达波角计算

在此过程中对各个散射体的发射方位角(AoD，φd)、发射仰角(EoD，θd)、接收方位角(AoA，φa)以及接收仰角(EoA，θa)进行计算[11]。

首先，假设所有散射体的功率角度谱均服从高斯分布。由于在假设中功率角度谱是连续的且信道内的路径是离散的，与实际不符，为减小最终算出的角度结果误差，需要引入函数Cφ(L,K)。此外，为保证能量最高的路径的角度为0，且其余路径的角度与功率有关，构造式(6)：

(6)

(7)

由于仰角的范围是[-π/2,π/2]，故对θd，θa作修改：

(8)

由于发射机、接收机的位置固定，因此LOS径的角度固定，故以LOS径的角度对上面计算的各种角度值进行校正[12]。

(9)

最后，将各个波簇路径均分为20个子径，以此估计散射体内部的角扩展。

(10)

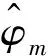
表1 子径偏置角

子径编号m偏置角φ^m/(°)子径编号m偏置角φ^m/(°)1,2±0.044 711,12±0.679 73,4±0.141 213,14±0.884 45,6±0.249 215,16±1.148 17,8±0.371 517,18±1.519 59,10±0.512 919,20±2.155 1

1.5 达波角、时延和相位偏移校正

在移动MIMO信道模型中，接收端运动会引起达波角、射线传播距离和射线极化的变化，从而引起相应的小尺度衰落[13]。为进行时间连续的信道建模，需对信道中某些小尺度参数的偏移现象进行定量分析。卫星移动MIMO信道的小尺度参数偏移示意图如图2所示。

图2中，LBS为射线从发送端到接收端所经过路径的最后一个散射体，r为发射天线编号，t为接收天线编号，l为波簇编号，s为采样点编号。根据初始达波角和散射体时延计算出LBS的位置，分别对LBS和终端移动轨迹上的所有采样点之间的角度和距离进行计算。

假设不同子信道的长度dl、时延τl以及发射机的发射角均相等，只是接收机的达波角不同。NLOS径信号传播距离并据此计算出相位和时延偏移：

(11)

1.6 极化耦合

信号在信道中传播时，由于信道的一些特性，会使传播信号的极化角度产生偏转[13]，如图3所示。

图3中，pr为电磁波经过信道传输后到达接收天线时的极化方向or在垂直于电磁波传播方向的平面上的投影，Ft，Fr分别为发射天线和接收天线对电磁波极化的响应。

双极化GEO卫星移动MIMO通信系统中，发射天线和接收天线的天线增益都是确定的，且经实验证明[14]，电磁波在传播过程中极化方式不变，仅极化角度有所改变，因此需对计算pr和Fr之间的偏置角ϑ进行计算，建立极化耦合矩阵M，以达到极化耦合的目的。对于LOS径，可计算出ϑ和M。

(12)

1.7 信道增益初步计算

完成以上计算后，本文利用天线方向图、射线的极化和相位来对信道段中的各个采样点计算初始信道增益。通过发射天线、接收天线的极化响应和极化耦合矩阵来计算极化增益。

各多径分量都有一个初始相位ψ0。为将各个波簇都等效为一条路径，可将各个波簇对应的20条子径进行加和，得到随机的波簇功率，然后信道段内所有采样点的平均能量并获得初步的信道增益：

(13)

(14)

(15)

式中，Pl为各波簇的初始功率。

1.8 引入PG，SF，KF的信道增益计算

利用SF,KF的相关图中数据对式(15)中计算得到的信道系数初值进行完善：

(16)

(17)

式中,Ks,SF[dB]s分别为KF和SF相关图上在采样点s处的值，K0为KF在初始位置处的值。

1.9 信道段过渡

以上计算均在移动终端轨迹上的一个个信道段内分别独立进行。然而在信道建模的过程中应在移动终端的运行轨迹内对射线实现完全追踪，因此需要考虑信道小尺度参数和大尺度参数在不同场景信道段内的平滑过渡。

本文仅考虑功率和相位这2种小尺度参数在信道段内的过渡。对于需要考虑信道段过渡的所有参数，均使用平方正弦函数来使其在整个空间域内保持平滑，其为值域为[0,1]的线性函数：

(18)

2 实验结果与分析

2.1 仿真场景

对于建立的信道模型，采用以下部分进行初步的实现与验证，验证的仿真场景如图4所示。

图4 仿真场景示意图

图4中，卫星为配有双极化天线的GEO卫星，仰角为35°，地面移动终端上配有双极化全向天线。地面移动终端运动速度为10～120 km/s。在简单模型中假设短暂时间内移动终端所处范围均为MIMOSA_10-45_LOS和MIMOSA_10-45_NLOS场景，分别代表10°～45°仰角下城区直射场景和10°～45°仰角下城区非直射场景。2种场景的大尺度参数及各种大尺度参数之间的互相关系数如表2、表3和表4所示。

表2 2种场景的大尺度参数

参数MIMOSA_10-45_LOSMIMOSA_10-45_NLOSμσλμσλKF15.505.94.5-6.303.73SF03.63506.535AsA1.500.231.51.800.218AsD-4.600.11 000-4.600.11 000EsA1.400.161.300.215EsD-5.120.11 000-5.120.11 000

表3 MIMOSA_10-45_LOS场景大尺度参数互相关系数

参数DSKFSFAsDAsAEsDEsADS1.00-0.460.4300.610-0.05KF-0.461.00-0.300-0.440-0.03SF0.43-0.30100.5600.18AsD0001000AsA0.61-0.440.560100.15EsD0000010EsA-0.05-0.030.1800.1501.00

表4 MIMOSA_10-45_NLOS场景大尺度参数互相关系数

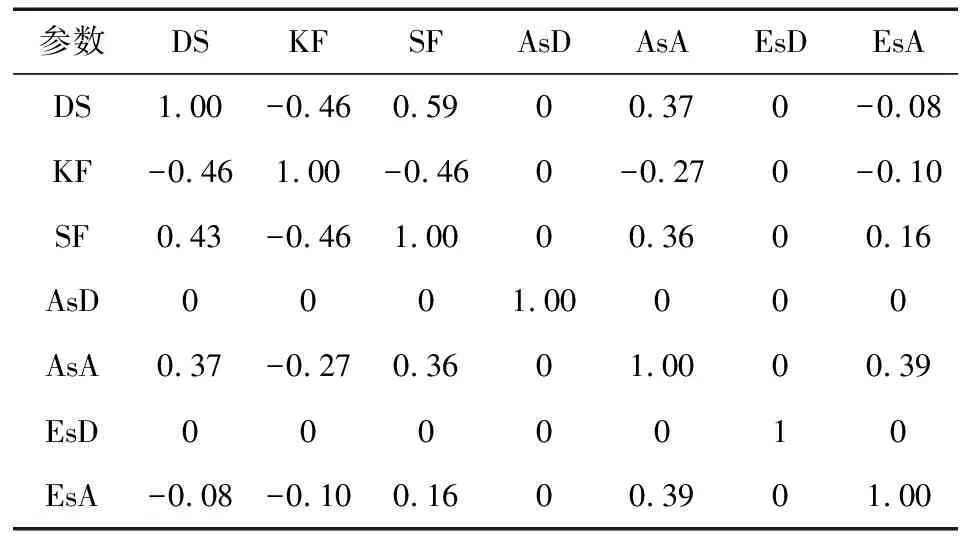
参数DSKFSFAsDAsAEsDEsADS1.00-0.460.5900.370-0.08KF-0.461.00-0.460-0.270-0.10SF0.43-0.461.0000.3600.16AsD0001.00000AsA0.37-0.270.3601.0000.39EsD0000010EsA-0.08-0.100.1600.3901.00

2.2 仿真过程与结果

随机模拟移动终端的运动轨迹速度，得出对移动终端进行采样所得的采样点。对2个采样点之间的信道环境的直射性进行随机模拟，得出双极化卫星移动MIMO系统示意图如图5和图6所示。

图5 系统示意图

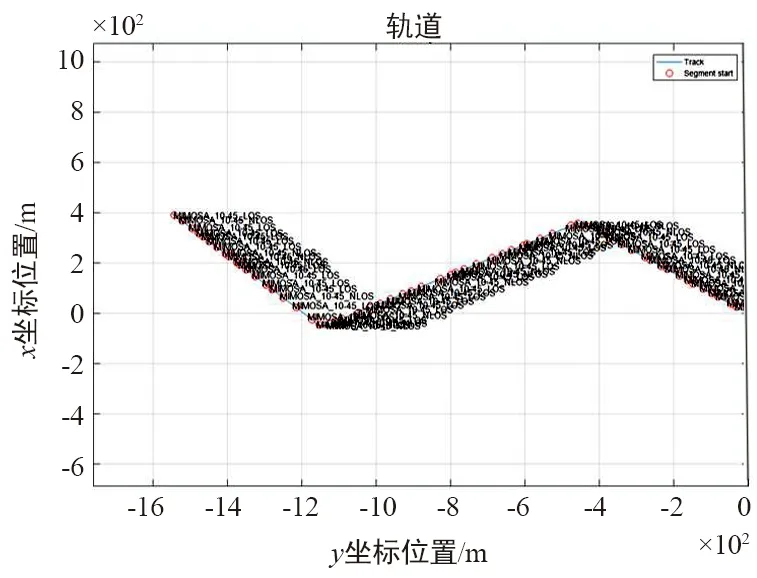
图6 终端轨迹

根据基于几何统计的建模方法对系统信道中的传输射线进行追踪，得出各条射线的各种小尺度参数。对小尺度参数进行处理可得以下仿真结果。

2.2.1 运动轨迹上接收信号功率

通过对各采样点处的接收信号功率进行矢量加和可得移动终端运动轨迹上双极化接收信号的功率变化如图7所示。对比图6和图7发现，图7中直射区域和非直射区域与图6中直射段和非直射段完全一致，接收信号在直射区域和非直射区域有显著区别，而且在同一段区域内，同圆极化波的功率显著大于正交圆极化波的功率，且二者的变化趋势相似，符合实际情况。

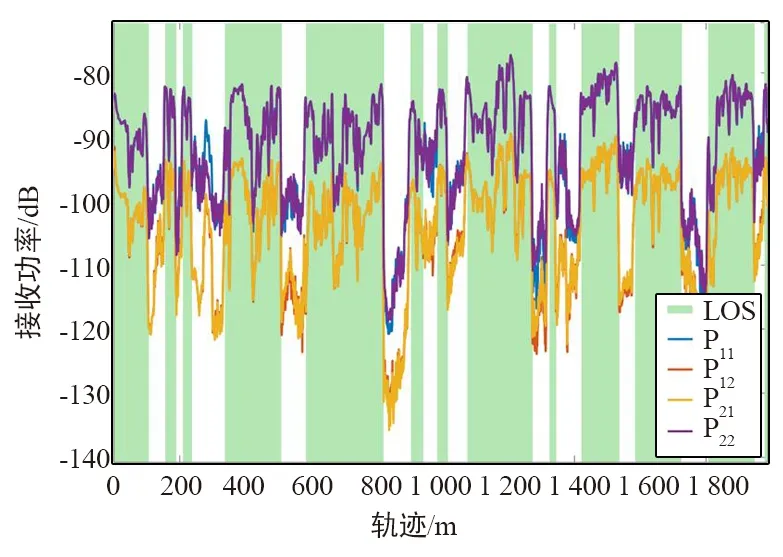
图7 运动轨迹上双极化信号的接收功率

2.2.2 接收信号的功率时延谱

对接收信号的功率和相对时延进行统计，可得接收信号的功率时延谱如图8所示。将图8与图6和图7进行比较，发现图8所示区域的LOS性与图6和图7完全一致。对功率时延谱进行分析发现，在直射区域和非直射区域内，信号均在相对时延为0处功率最大，与“直射”分量功率最大理论一致；此外，在直射区域内信号的功率明显高于在非直射区域内信号的功率，且较大时延对应的信号功率也更大，与实际情况相符。

图8 运动轨迹上接收信号的部分功率时延谱

2.2.3 接收信号的统计特性

根据卫星移动MIMO信道统计特性和文献[7]中使用增强型统计模型对以上介绍的双极化卫星移动MIMO信道的仿真成果，本文计算了信道的功率累积分布(PDF)、平均衰落持续时间(AFD)和电平通过率(LCR)，并与文献[7]中的仿真结果进行了对比。仿真结果及对比如图9～图11所示。

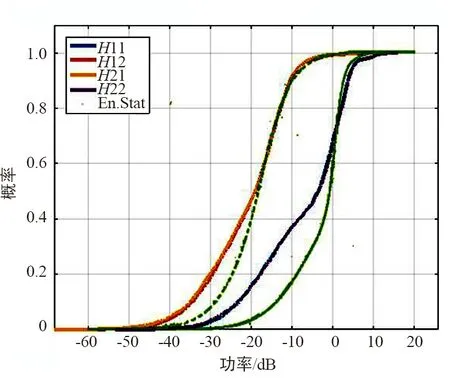
图9 双极化卫星移动MIMO信道功率累积分布

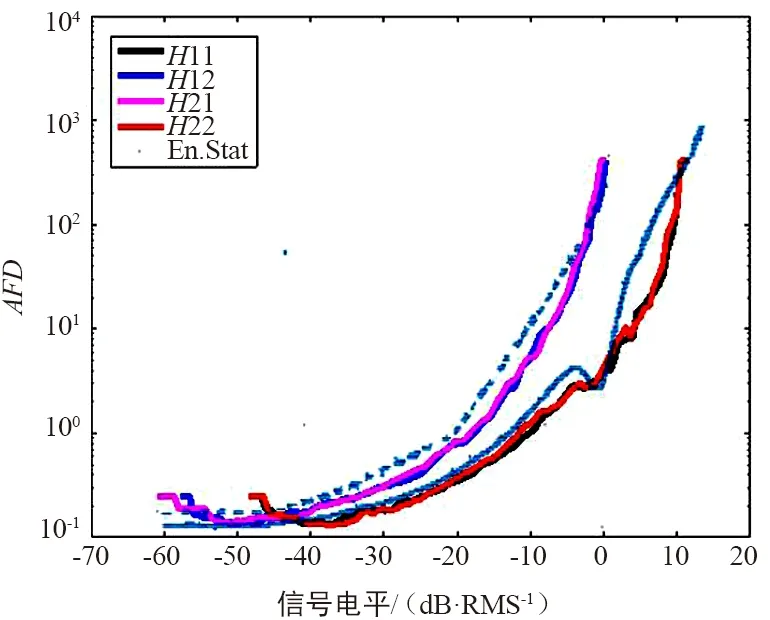
图10 双极化卫星移动MIMO信道平均衰落持续时间

图11 双极化卫星移动MIMO信道电平通过率

图9～图11中的蓝色线条均为文献[7]中的仿真结果，其中实线代表同极化信号的统计特性，虚线代表正交极化信号的统计特性。由以上3图对比可看出，基于几何统计的信道模型仿真得到的3种统计特性均与文献[12-13]的仿真结果相近，因此可证实建立信道模型的正确性。此外，在平均衰落持续时间和电平通过率的仿真结果中，所建模型的仿真结果曲线较为平滑，而文献[7]的仿真结果曲线在0 dB处有明显的凸起，经分析，这种结果是统计模型中以直射分量为准、以直射分量为主的建模思路所导致的结果[15]，而本文基于几何建模的总体思路则有效地规避了这一问题。由此，所建立的信道模型达到了结合统计建模和几何建模二者优点的目标，实现了以一定复杂度为代价提高信道模型准确性的目的。

3 结束语

从双极化卫星移动MIMO信道建模问题的角度出发，分析了多种现有信道建模像方法以及其优缺点，提出了基于几何统计的建模理论。

该模型总体上使用几何模型的建模思路，采用射线追踪方法对信道中传输的射线进行追踪，重点关注各条射线的多种小尺度参数，在实际计算中引入统计学方法对小尺度参数进行建模与处理，同时考虑了信道环境造成的信号衰减以及信道环境对射线极化的影响。在实验过程中，在一定场景下对该信道模型进行了仿真，并将这种场景下信道的各种统计特性与使用增强型统计模型仿真出的统计特性进行了比较。实验表明，本文所建立的双极化卫星移动MIMO信道模型可以真实地反映卫星移动MIMO信道的信道特性，同时可以克服统计模型的一部分缺陷，是一种结合几何模型和统计模型优点的具有良好性能的双极化卫星移动MIMO信道模型。

此外，该模型具有良好的普适性，在不同的实际场景下，可以根据具体需求对该方法进行改进。