水下空气腔角反射器声散射特性

罗祎，陈鑫

(海军工程大学 兵器工程学院，湖北 武汉 430033)

0 引言

目前在水下对抗中，模拟舰艇目标的声反射强度和尺度特征以诱骗主动声探测，通常采用的是接收应答方式[1-2]。这种工作方式技术复杂、造价高且实时性差，易被主动声纳识别。

角反射器是一种强回波装置，通常用于雷达对抗领域[3]，如英国DLF-1橡皮鸭八面角反射体、以色列宽频打击雷达诱饵Wizard[4]。利用水下角反射器无源模拟舰艇等目标的水声特征，是一种对抗主动声纳探测的新技术途径[5]。水下角反射器构造简单、价格低廉、使用方便且适用性强[6]。因此，研究水下角反射器的声散射特性、提高其反声性能具有重要意义。

雷达角反射器的研究与应用已经比较成熟，但水下角反射器与空气中雷达角反射器的反射机理并不相同，相关文献很少。文献[6]提出了声束弹跳法，将其应用于水下角反射体声散射计算，该方法在计算的收敛性及精度方面需要进一步提高。文献[7]应用修正声束弹跳方法快速预估水下圆形角反射体散射声场，降低了计算量。文献[8]分析了不同金属材料二面水下弹性角反射器的声散射特性，结果表明水下单层金属板角反射器具有强烈的频率特性，目标强度小，散射宽度小，在模拟舰艇声反射强度时需要的尺寸和质量较大，不便于工程应用。

由于空气与水的特性阻抗严重失配，水下空气层反声效果比金属薄板好，可以据此提高角反射器目标强度。此外，水下角反射器是一种浸水薄壁结构，在计算其声散射特性时必须考虑流体介质及其对结构振动产生的重要影响[9-10]。有限元耦合间接边界元法是求解水下弹性目标声辐射或声散射问题的一个重要趋势[11-12]。此外，角反射器是一种凹形结构，计算其散射声场时不能忽略多次散射波的贡献[13]。声学软件SYSNOISE对目标进行声学仿真时会考虑声的反射、衍射和折射等行为，便于计算凹面结构散射声场[14]。

因此，本文以空气腔反声板为基础，构造水下弹性空气腔角反射器，以提高其目标强度。采用有限元软件ANSYS和声学软件SYSNOISE对水下弹性空气腔角反射器的声散射特性进行仿真分析，对比了单层金属板角反射器和空气腔角反射器的散射特性，并对结果进行了实验验证，进而为水下角反射器的设计和应用提供了参考依据。

1 水下角反射器声散射计算方法

本文采用结构有限元耦合流体间接边界元法计算水声角反射器声散射，下面推导该方法的流体- 固体耦合方程。

假设物体处于理想流体中，Q为结构表面S上的任意一点，n为Q点的外法线单位矢量，P为空间中的任意一点，A点为声源，O点为结构的声学中心。间接边界元示意图如图1所示，图1中rP、rQ、rA分别为O点到P点、Q点、A点的向量。

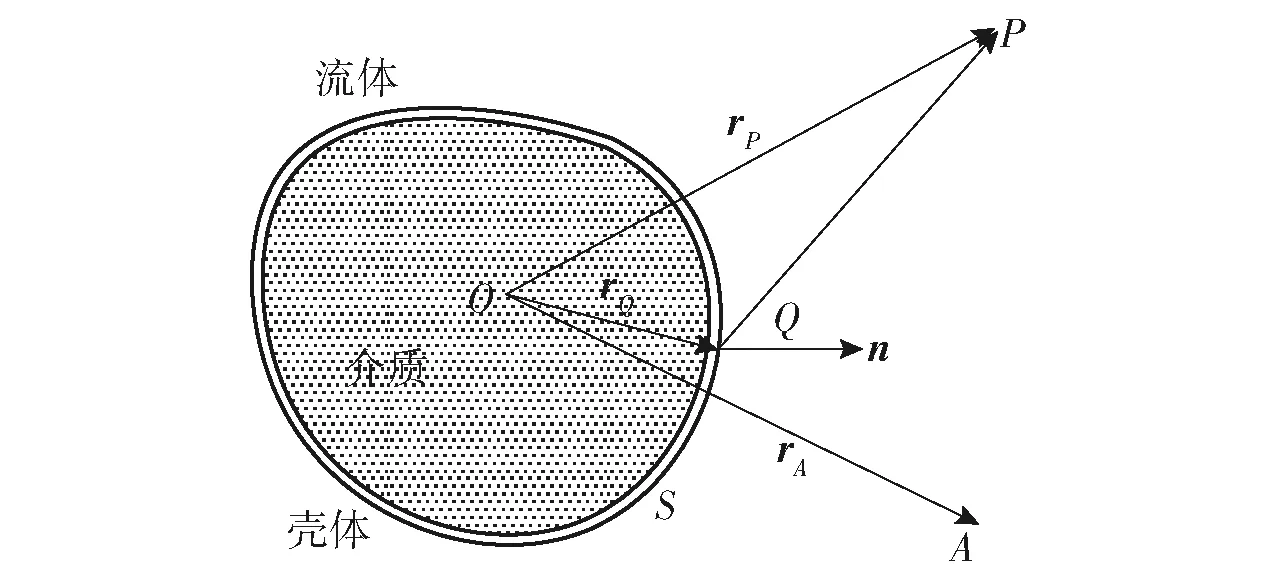
图1 间接边界元示意图Fig.1 Schematic diagram of indirect boundary element

根据波动方程，可以推导出直接边界元法单频散射声场的Helmholtz方程为

(1)

式中：p为瞬时声压；p(rQ)为Q点的声压；G(rP,rQ)=e-jk|rP-rQ|/(4π|rP-rQ|)为格林函数，k=ω/c为波数，ω为圆频率，c为流体中的声速；ρ为流体密度；vn为Q点的法向振速；p(rP)为P点的声压。

由直接边界元法可推出间接边界元法，得到任意场点的声压为

(2)

式中：σ(rQ1,rQ2)和μ(rQ1,rQ2)分别为表面两侧法向压力梯度差和压力差，

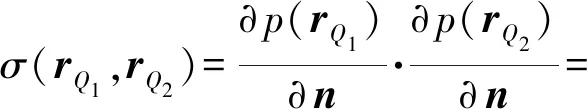
(3)

μ(rQ1,rQ2)=p(rQ1)-p(rQ2)，

(4)

v(rQ1)、v(rQ2)分别为表面两侧法向振速，p(rQ1)、p(rQ2)分别为表面两侧声压。

设边界表面满足Neumann条件，将P点定义在边界上，可得边界条件和未知变量的关系为

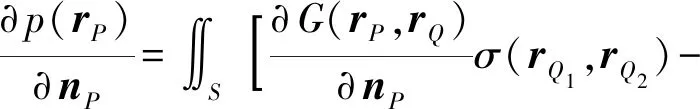
(5)

式中：nP为P点的外法线单位向量；v(rP)为P点的振速。根据变分原理，可以推导出一般形式为

Ax=Fa，

(6)

式中：A为对称矩阵；x为边界元模型表面的未知变量，即σ(rQ1,rQ2)或μ(rQ1,rQ2)；Fa为声激励向量函数。

对于水下弹性目标的声散射问题，假设结构阻尼为0，则在物理坐标系下，有限元结构模型和间接边界元流体模型无损耗耦合系统方程为

(7)

计算得到边界表面的未知变量后，可求解空间任意场点的声压和声强，从而得到相应的目标强度值为

(8)

式中：|Ir|r=1为根据球面波扩散规律换算到距目标等效声源中心1 m处的散射声强；Ii为入射声强。

2 仿真实验及对比分析

由于空气层具有较强的压缩性，在水压作用下会影响反声效果，构造如图2所示带有空气腔的薄钢板，钢板厚度为1 mm，将薄金属板焊接成封闭空气腔平板，内设一定数量的加强筋增强结构强度和耐压性，避免空气层受压。利用空气腔薄板构造角反射器，由于表面金属很薄，反射系数很低，几乎可以当作透声膜。

图2 空气腔平板示意图Fig.2 Schematic diagram of air-filled cavity plate

下面利用ANSYS和SYSNOISE软件，对弹性空气腔角反射器和单层薄钢板角反射器的散射声场进行仿真计算，并对比分析其散射特性。

2.1 二面角反射器对比

图3所示为平面波入射到二面角反射器的示意图。图3中：l为二面角反射器边长，l=1 m；φ为入射波与Oxz平面的夹角；θ为入射波与z轴的夹角；h为角反射器板厚；B为入射平面波点，波幅值为1 Pa；r为声源与目标的距离，r=100 m，满足远场条件。单层薄钢板角反射器钢板厚度分别为5 mm、10 mm和20 mm，弹性空气腔角反射器表面钢板厚度为1 mm，空气层厚度为20 mm，水的密度ρ=1 000 kg/m3，水中声速c=1 480 m/s. 入射波频率范围为5～20 kHz，场点设在声源处(收发合置)，不计结构阻尼。

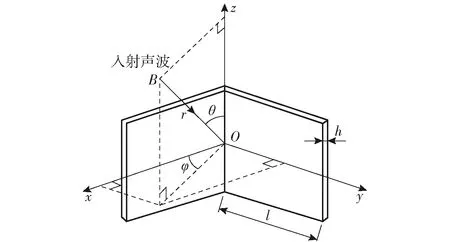
图3 平面波入射到二面角反射器的示意图Fig.3 Schematic diagram of plane wave incident on biplanar corner reflector

2.1.1 入射频率的影响

根据以上仿真条件，分别计算空气腔角反射器和厚度为5 mm、10 mm、20 mm的二面单层金属板角反射器目标强度频响曲线，仿真结果如图4所示。

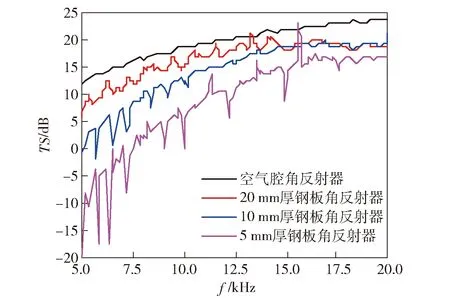
图4 空气腔角反射器的目标强度Fig.4 Target strength of air-filled cavity corner reflector

由图4可见：

1)空气层厚度为20 mm的空气腔角反射的目标强度，比钢板厚度为20 mm的弹性角反射器的目标强度值大3～5 dB，比10 mm厚的弹性角反射器大5～10 dB，比5 mm厚的弹性角反射器大10～20 dB.

2)随着频率的增大，单层金属角反射器的目标强度逐渐增大，最后趋于一个定值。这是因为频率的增大，使薄板的反射系数增大，镜反射逐渐增强。单层金属薄板角反射器目标强度变化曲线存在明显的频率特性，曲线随频率变化呈极大、极小值变化，这主要是由声波入射到水中弹性结构表面而激起结构的某些共振模态引起的。

3)对于水中空气腔角反射器，当频率增大时，角反射器镜反射增强，目标强度先增大、后趋于平稳，不存在明显的频率效应。

由此可见，水中空气腔角反射器反声效果良好，具有去耦作用。

2.1.2 入射角度的影响

12枚编号限量发行的Arceau“RobeduSoir”腕表将当代马赛克嵌花工艺与爱马仕玩味十足的创意世界巧妙融合。

图5 θ为90°和φ为0°～90°时的目标强度(空气腔)Fig.5 Target strength for θ=90° and φ being equal to 0°-90° (air-filled cavity)

图5、图6所示分别为空气腔二面角反射器和厚度为20 mm的金属钢板二面角反射器目标强度随入射角度变化的曲线。由图5和图6可以看出，空气腔角反射器的目标强度变化曲线更平滑，且同一角度下的目标强度值比单层金属板角反射器大。此外，空气腔角反射器的散射宽度也大于单层金属板角反射器。

图6 θ为90°和φ为0°～90°时的目标强度(单层金属板)Fig.6 Target strength for θ=90° and φ being equal to 0°-90° (single layer metal plate)

2.2 三面角反射器对比

在一般工作情况下，声波是以一定空间角度入射到角反射器平面的，其回波信号由镜反射波、多次散射波和再辐射波组成，回波强度与入射角关系复杂。本文选择三角形薄钢板角反射器和三角形弹性空气腔角反射器作为研究对象，分析声波从不同角度入射时角反射器的目标强度变化情况。平面波入射到三面角反射器的示意图如图7所示。分别定义入射角度φ为45°、θ为0°～90°和θ为55°、φ为0°～90°，观察其目标强度值在不同频率条件下的变化情况，仿真结果如图8和图9所示。

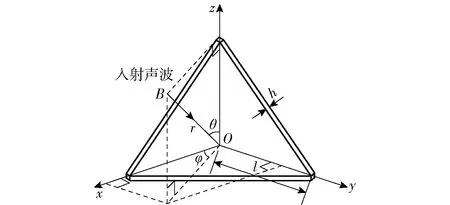
图7 平面波入射到三面角反射器的示意图Fig.7 Schematic diagram of plane wave incident on trihedral corner reflector

图8 φ为45°和θ为0°～90°时的目标强度Fig.8 Target strength for φ=45° and θ being equal to 0°- 90°

由图8和图9可见：

1)薄钢板角反射器和空气腔角反射器的变化规律基本相同，但薄钢板角反射器的目标强度曲线随入射角度的变化起伏明显，反声效果不佳；而空气腔角反射器目标强度曲线随入射角度的变化平缓，在绝大部分入射方向上，目标强度大于同样尺寸薄钢板角反射器，反声效果好。

2)两类角反射器在不同频率条件下的目标强度变化趋势相同，频率越大、目标强度越大。

3)当入射角度θ为55°、φ为45°时，三角形角反射器的目标强度达到最大值，该角度与文献[6]中刚性三角形角反射器的仿真结果一致。

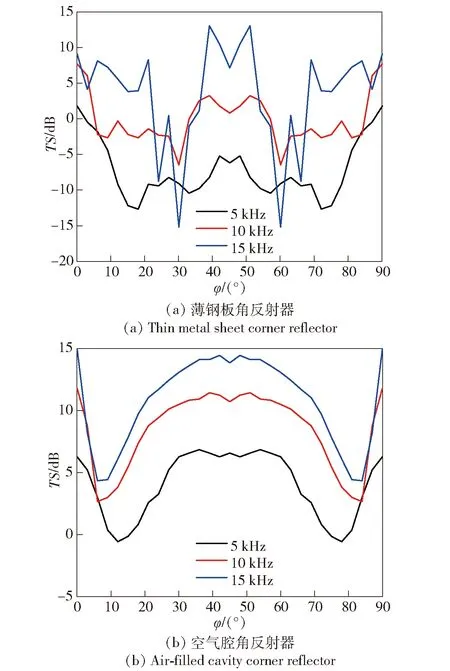
图9 θ为55°和φ为0°～90°时的目标强度Fig.9 Target strength for θ=55°，and φ being equal to 0°-90°

3 消声水池实验验证

薄钢板角反射器的声散射在文献[8]中已进行了验证。为了验证空气腔角反射器仿真计算结果的正确性，本文设计加工了边长为0.5 m、空气层厚度为20 mm的三角形空气腔角反射器，在大型消声水池对其目标强度进行实验测量。

图10 水池实验布放示意图Fig.10 Schematic diagram of experimental layout in pool

图11 水池实验布放现场Fig.11 Scene of experimental layout in pool

用水听器接收的声信号电压值表示目标强度：

(9)

式中：Ui为入射信号电压值；Ur为离目标声源中心1 m处反射信号电压值；Ub为目标回波信号电压值；Ud为直达波电压值。实验结果如图12和图13所示。

由图12和图13可见，三角形空气腔角反射器目标强度的仿真结果与实验结果基本一致，从而验证了计算结果的正确性，也证明了空气层对于增大角反射器回波强度的贡献。实验结果与仿真结果存在一定的误差，但处于合理范围内，主要原因是角反射器加工时反射面存在垂直度误差。

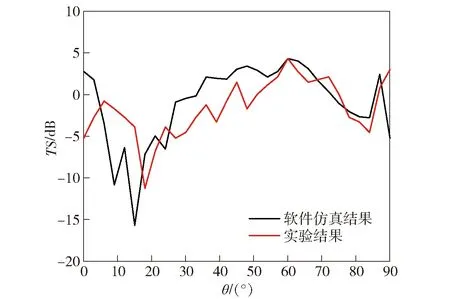
图12 φ为45°和θ为0°～90°时的目标强度Fig.12 Target strength for φ=45° and θ being equal to 0°-90°

图13 θ为55°和φ为0°～90°时的目标强度Fig.13 Target strength for θ=55° and φ being equal to 0°-90°

4 结论

本文根据空气和水的声特性阻抗严重失配的特点，设计了一种新的水下空气腔角反射器。采用结构有限元耦合流体边界元法，计算了空气腔角反射器的散射特性，并与薄钢板角反射器进行了对比分析，对仿真结果进行了消声水池实验验证。结果表明，水下空气腔角反射器反声性能良好，无明显频率特性，散射宽度大且具有良好的去耦作用，同时其质量比同样目标强度的金属板角反射器轻，便于工程应用，是较为理想的声反射装置。

限于篇幅，本文只对单个水下空气腔角反射器的声散射特性进行了分析。对于多个角反射器组成的多格反射器声散射特性，以及如何精确模拟水下目标声散射等问题，还需要进一步研究。