基于投影法的GPU并行计算研究

李 刚，孙东亮，齐亚强，陈 帅，宇 波

(1.北京化工大学机电工程学院，北京 100029；2.北京石油化工学院机械工程学院，北京 102617)

流动传热是一种非常复杂的物理现象，广泛存在于石油、化工、冶金、能源等工业中，如化学、制药工业中的蒸发器和反应器；制冷工业中的冷凝器；核电站的蒸汽发生器、换热器；海上平台石油开采和精炼等都存在流动传热现象。目前，针对流动传热现象研究的方式主要采用试验的方法，但是该方法受到投资大、周期长、优化困难等一系列缺点的限制，难以满足工程领域不断增长的需求[1]。随着科学技术的创新、计算机技术的进步以及现代流动传热计算方法的不断完善，计算流体力学(CFD)成为研究流体力学各种物理现象的重要手段。流动传热的数值模拟已经取代了一些昂贵的、危险的、难以实现的试验，极大地降低了研制成本，缩短了研制周期。数值模拟方法在研究流动传热问题方面得到广泛地应用。然而，随着所涉及的流动传热问题复杂程度不断提高，方程数量变多，方程求解的难度变大，计算耗时大幅增加。如何快速求解这些复杂的流动传热问题成为学者研究的热点。

近年来，图像处理器(graphics processing unit，GPU)强大的浮点运算能力逐渐得到开发，与传统数值计算所用的CPU相比，GPU有着计算能力强、精度高、并行能力强以及可移植等特点。为了快速求解这些复杂的流动传热问题，国内外学者结合高效的GPU并行计算，完成了部分基于GPU并行计算的求解算法的研究。早在2008年，Brandvik等[2]利用GPU实现了三维Euler方程的快速求解，获得了16倍的加速效果，该研究最初验证了GPU应用在CFD领域的有效性。Williams等[3]研究出了一种基于GPU共轭梯度求解器，专门求解大型的线性方程稀疏系统，进而减少CFD分析时间。Jin等[4]开发了一个基于GPU的三维非结构化几何多网格解算器，有效地解决了非结构化三维网格的热传导问题。在160万的网格规模下，获得了24倍的加速倍数。彭峻等[5]通过改进WENO算法使其适合GPU加速，实现了高精度可压缩流的GPU计算，并获得了18倍的加速效果。鞠鹏飞等[6]为了实现隐式LUSGS时间推进，采用层内GPU并行方法得到的加速倍数为8.89倍。

在流动传热问题的数值模拟中，最重要的部分是对Navier-Stokes(N-S)方程组的求解。非原始变量法和原始变量法是2种最常用的求解算法。在非原始变量法中最具代表性的方法为涡量-流函数法[7]。该类方法求解方程组时要引入新的变量，所求的结果并不是速度和压力场，边界处理较为复杂，应用相对较少。原始变量方法的最大优点是不仅边界处理相对简单，而且可以直接计算出所需要的压力场和速度场，所以应用较为广泛，发展也相对较快。针对非稳态流动传热的数值模拟，在求解N-S方程组原始变量的主要算法中投影算法应用较为成熟，该方法被普遍应用于有关CFD问题的求解。但是随着非稳态流动传热问题研究的深入，如针对复杂区域的三维问题，网格数量通常高达百万或千万，通常需要几天甚至几个月的时间才能获得一个收敛结果，远远不能适应工程上快速设计的要求。为了实现非稳态流动传热问题的快速求解，笔者开发了基于投影法的GPU并行计算策略，并以二维顶盖驱动流为例研究了GPU并行计算求解性能。

1 控制方程及离散

1.1 控制方程无量纲化

针对二维顶盖驱动不可压缩流，以方腔的长度和高度H、流体密度ρ、顶盖拖动速度utop作为无量纲标尺，将原有N-S控制方程组无量纲化[8]：

质量守恒方程：

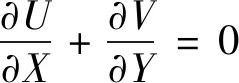
(1)

动量守恒方程：

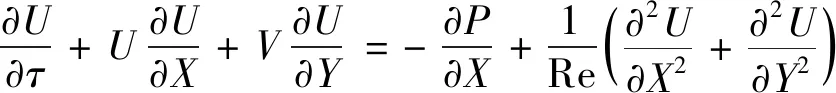
(2)

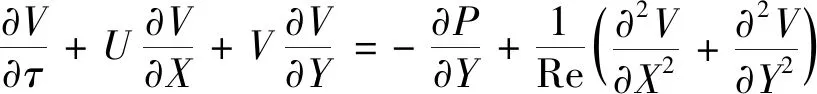
(3)

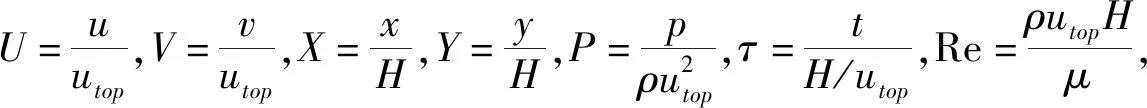
1.2 方程离散

对于投影算法，中心差分格式被用于离散方程中的导数[9-10]。针对压力梯度项采用隐式格式，速度项采用显示格式，Δτ为时间步长，ΔX、ΔY为空间步长。

对速度分量U进行离散：

对于内点处理：

非稳态项：

(4)

对流项：

(5)

(6)

扩散项：

(7)

(8)

压力项：

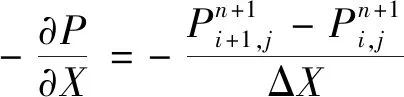
(9)

(10)

(11)

离散化后的动量方程：

(12)

同理可得：

(13)

连续性方程离散：

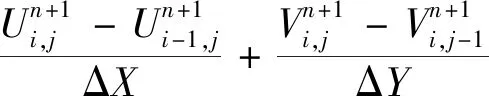
(14)

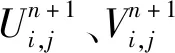
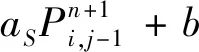
(15)

其中：

2 投影法

为了快速准确地求解N-S方程组，投影法实现的方式是对该方程组的速度压力进行解耦求解，且速度和压力解耦后无需要求速度-压力的插值函数满足Ladyzhenskaya-Babuska-Brezzi(LBB)相容性条件[11]。该条件目的为实现速度-压力混合有限元求解的稳定，但是实现该条件的求解过程较为复杂。而投影法的主要思想为在原有方程中引入一个无需要满足散度为零的中间变量，分开计算速度和压力，从而无需满足该条件。

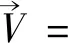
(16)

其中：η满足·η=0，因此投影法实施过程中通过在N-S方程中引入1个无散度适量，该变量可以表示为1个无旋(有势)矢量场与无散度速度场之和：

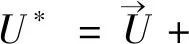
(17)

首先，通过一阶离散的方式将N-S方程中的时间导数项进行离散，得到1个半离散化方程：

(18)

(19)

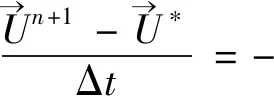
(20)

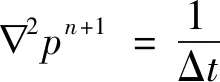
(21)

式(21)的右端项由步骤①计算，而压力pn+1项在给定的边界条件下能够求出。

(22)

总之，当利用投影法求解下一时刻的压力场和速度场时，动量方程和连续性方程不需要重复迭代，只需要通过上述3步就能完成求解。

3 CUDA编程模型

CUDA是一个用于CPU+GPU异构系统的通用并行计算架构。该架构的最大优势是降低了GPU通用计算的编程门槛，研究人员不需要掌握复杂的图形知识就可以直接使用C/Fortran等语言为CUDA架构编写程序，因此该架构在计算流体力学(CFD)并行计算方面得到广泛地应用[13-14]。笔者采用NVIDIA的CUDA编程模型实现基于投影法的GPU并行计算研究。

在CUDA架构中，GPU主要处理并行计算任务。而主控制逻辑任务和串行计算部分则由CPU完成。CUDA的编程模型如图1所示。图中的内核(kernel)函数表示在算法中并行的步骤。由图1可以看出，并行性包含2个层次(或粒度)：一个是在线程网格(grid)中线程(thread)块与线程块之间的并行；另一个是线程块中线程之间的并行。对于大多数CFD算法而言，网格的划分模式将显著影响GPU上程序的效率，最高效的方式是1个网格节点对应1个线程。此外，内存组织和通信重叠也对程序的效率有重要影响，因此良好的网格划分模式也应该满足对线程束(warp)全局内存的联合访问。但是，没有一种通用的优化方法适用于GPU上的所有并行算法，关于如何划分网格、组织内存等，需要针对不同的问题进行不同的分析和优化。

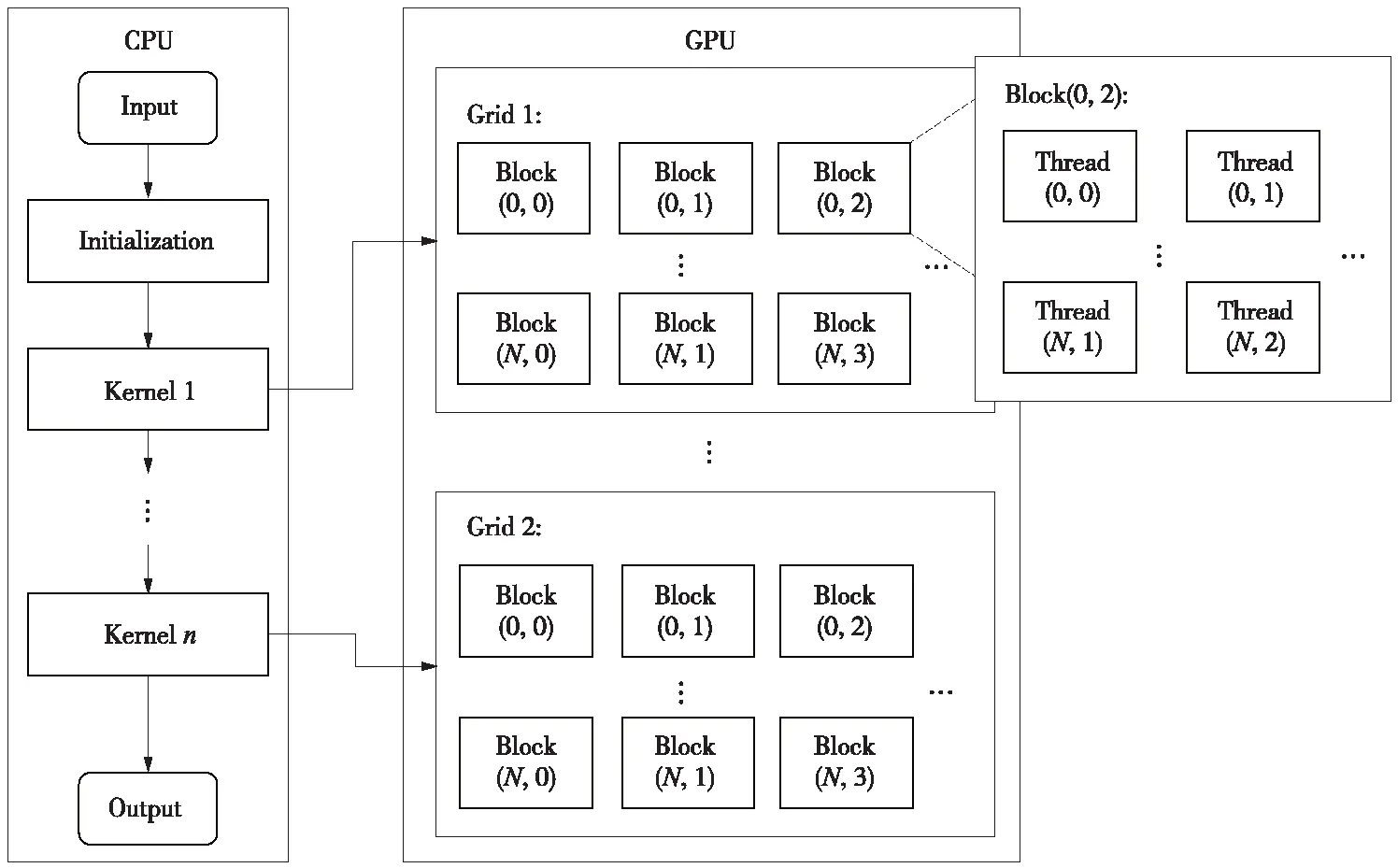
图1 CUDA编程模型Fig.1 CUDA programming model

4 投影法的GPU并行化

4.1 投影法的分析

GPU强大的浮点运算能力能够使投影法快速而高效地实现，但这并不等于算法中所有的运算过程都适合在GPU上进行并行计算，因此该算法的关键问题在于找出合适的部分交由GPU来并行计算。GPU与CPU架构不同，前者的设计目的是面向矩阵类型的数值计算，而后者的设计目的是面向指令的高效执行，因此前者更擅长于高度并行的复杂计算，而后者却擅长执行程序以及复杂逻辑事物。通过研究投影法的具体步骤可以发现，在进行计算中间速度U、V以及迭代求解压力P时，各个子块之间相关性不大，可以同时进行运算，符合并行计算的前提；另外，算法的性能瓶颈主要在迭代计算过程中，尤其是当网格规模较大时，传统的CPU串行计算无法满足快速计算的要求。为此，采用CUDA架构线程块通过GPU的并行计算能力实现投影法的求解，从而提高算法的运行速度。

4.2 并行过程设计

适合并行计算的部分为中间速度U、V以及压力P的求解。对于控制方程的离散方式是基于交错网格系统[15]，即中间速度U、V以及压力P分别对应1套网格，具体如图2所示。

图2 交错网格系统Fig.2 Staggered grid system

为了达到在GPU中并行的目的，通常是1个线程对应1个节点，当计算网格数目较大时，1个线程处理若干个节点。CUDA中线程组成线程块，所以自然把计算区域分解为若干个与线程块对应的区域，线程块的大小与维度由用户指定。在GPU上求解中间速度U、V时，首先需要将所需数据从CPU内存传输到GPU的全局储存器，然后根据网格大小数来确定所需最优线程块数以及每个线程块最优线程数，一般32个线程组成1个线程粒度(warp)。因此，尽可能地使每个线程块的线程数是线程粒度的整数倍，以实现高效的并行计算。然后将离散后的方程直接放入对应的核函数中进行并行求解，值得注意的是，当计算求解边界点时，由于二维数组中的1行或1列数值是已知的，因此可以直接转化定义为一维数组求解，以此来提高计算效率。在投影算法中，雅可比迭代法用于求解压力泊松方程。需要注意的是，当求解1个时层压力值后，一定要进行同步操作，以免造成不必要的错误。

4.3 投影法GPU并行计算流程

基于CUDA核函数的异步执行方式，实现了投影法的GPU并行计算。类似于Chen等[16]的实施方式，投影法的GPU并行计算流程如图3所示。

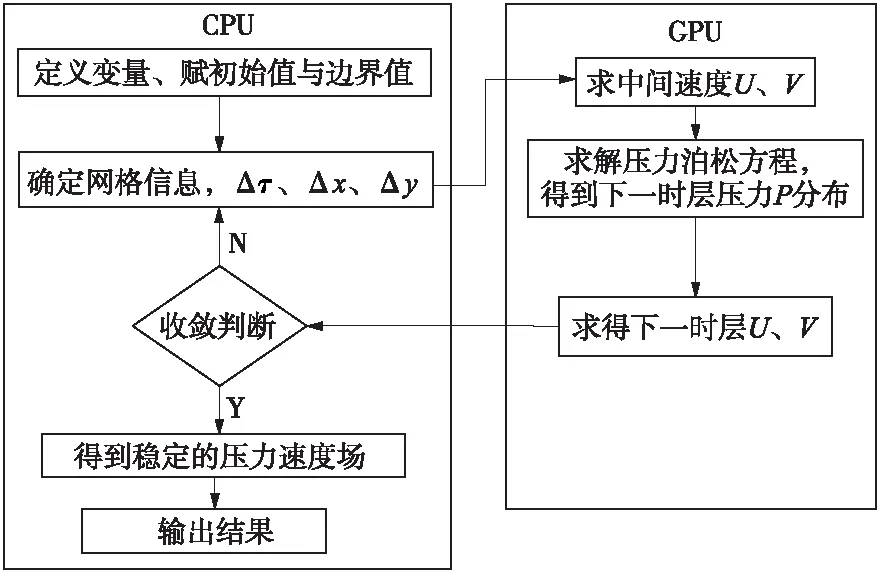
图3 投影法的GPU并行计算流程Fig.3 GPU parallel computing flow chart of projection method

整个工作分为两部分：一部分由CPU完成；另一部分由GPU完成。在CPU上完成不适合并行运算的工作，主要包括：定义变量、初始化数据、网格生成、获取网格坐标数据、误差收敛判断等。具体实现CUDA异构运算的过程为：当变量声明及存储空间分配后，将数据初始化，接着将数据拷贝到GPU的全局内存，依次使用3个内核函数完成中间速度U和V的求解、压力P的求解以及下一时层U和V的更新，最后将数据拷贝到CPU，进行收敛判断。如果满足收敛判断条件，则结束循环，输出结果。如果不满足收敛条件，则继续进行循环计算。

5 计算结果与分析

以二维方腔顶盖驱动流为例进行实验仿真。在数值试验中，GPU为NVIDIA Quadro K1200，拥有512个流处理器(SP)，显存带宽最高可达80GBps。CPU为Intel(R)Xeon(R)E5-1660 v4，CPU处理单元的频率是3.2 GHz。

当雷诺数Re=1 000、网格数为250×250时，基于投影法的GPU并行计算所得流场如图4(a)所示，该计算结果与文献[7](涡量-流函数)和文献[17](同位网格的SIMPLER算法，CPU并行)中给出的仿真结果[如图4(b)所示]一致，验证了该并行算法的正确性。以下对基于投影法的GPU并行计算方法求解性能进行分析研究。

5.1 雷诺数的影响

为了分析不同流动工况对GPU并行计算性能的影响规律，对比研究了不同雷诺数下CPU串行计算时间和GPU并行计算时间，这里雷诺数为无量纲准则数，决定了顶盖驱动流的流动工况。在不同网格规模下，Re=100、Re=1 000、Re=5 000时CPU串行计算时间如表1所示。从表1中可以看出，随着雷诺数的增加，CPU串行计算时间逐渐减少。相应的GPU并行计算时间如表2所示。GPU并行计算与CPU串行计算具有相同的规则，随着雷诺数的增加，GPU并行计算时间也逐渐减少。

图4 计算所得顶盖驱动流的流场图Fig.4 Velocity field of lid-driven cavity flow

表1 不同雷诺数下CPU串行计算时间

Table 1 Serial computation time of CPU under different Reynolds numbers

网格数串行计算时间/sRe=100Re=1000Re=500050×500.50.30.23100×1001053250×2501697644500×50053231853869

表2 不同雷诺数下GPU并行计算时间

Table 2 Parallel computation time of GPU under different Reynolds numbers

网格数并行计算时间/sRe=100Re=1000Re=500050×502.71.61.0100×100742250×250462012500×5001846530

为了衡量GPU并行计算性能，这里引入了GPU并行加速比的概念，定义为CPU串行计算时间与GPU并行计算时间的比值。在不同网格规模下，不同雷诺数时GPU并行加速比如图5所示。从图5中可以看出，雷诺数的变化也就是流动工况的变化，对GPU并行加速比几乎没有影响，这是由于在不同雷诺数下GPU并行计算时间与CPU串行计算时间具有相同的变化规律。

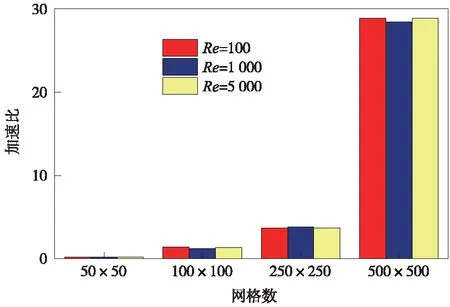
图5 不同雷诺数下GPU并行加速比Fig.5 Speed-up ratio of GPU parallel computation under different Reynolds numbers

5.2 网格规模的影响

随着所涉及的流动传热问题复杂程度不断提高，网格数量不断增加，对于三维复杂问题，网格规模通常高达百万或千万，计算耗时大幅增加，通常需要几天甚至几个月的时间才能获得1个收敛结果，远远不能适应工程上快速设计的要求，迫切需要开发适用于大规模网格的并行计算方法。因此，研究了网格规模对GPU并行计算性能的影响规律。

Re=1 000时不同网格大小的GPU并行加速比如表3所示。

表3 网格规模与GPU并行加速比的关系

Table 3 Relationship of speed-up ratio of GPU parallel computation and grid sizes

网格数CPU串行计算时间/sGPU并行计算时间/sGPU并行加速比50×500.31.60.2100×100541.2250×25076203.8500×50018536528.5

从表3中可以看出，当网格数量较小(50×50)时，GPU并行计算时间要大于CPU串行计算时间。这是由于网格规模较小时，GPU并行计算时间主要用于CPU与GPU之间的信息传递，从而降低其求解性能。随着网格规模的增大，CPU与GPU之间信息传递耗时所占的比例逐渐减小，所以GPU并行求解性能会不断提升。当网格规模从100×100增大到500×500时，GPU并行加速比从1.2大幅提高到28.5。由此可以看出，网格规模越大，GPU并行计算的性能优势越明显，而且在计算机本身固有的计算能力下，GPU并行加速比会随着网格数的增加持续增大。因此，GPU并行计算是一种非常适用于大规模网格的并行计算方法。

6 结论

为了实现非稳态流动传热问题的快速求解，开发了基于投影法的GPU并行计算策略，并以二维顶盖驱动流为例研究了GPU并行计算求解性能，得出以下主要结论：

(1)不同雷诺数下GPU并行计算时间与CPU串行计算时间具有相同的变化规律，因此雷诺数的变化对GPU并行加速比几乎没有影响，说明GPU并行计算适用于不同的流动工况，均具有相同的加速性能。

(2)随着网格规模的增大，GPU并行求解性能不断提升，当网格规模从100×100增大到500×500时，GPU并行加速比从1.2大幅提高到28.5。在计算机本身固有的计算能力下，GPU并行加速比会随着网格数的增加持续增大，说明GPU并行计算非常适用于大规模网格的计算问题。

虽然仅以经典的二维顶盖驱动流为例展开GPU并行计算求解性能研究，但对于不同流动传热问题，由于具有相同的GPU并行计算流程和信息传递方式，因此所得结论具有普遍适用性。