液气动量比对内混式直流气液喷嘴雾化特性影响

杨国华，张波涛，周立新，王 凯

(1.西北工业大学 航天学院 燃烧、热结构与内流场国家重点实验室，陕西 西安 710072；2.西安航天动力研究所 液体火箭发动机技术重点实验室，陕西 西安 710100)

0 引言

内混式直流气液喷嘴通过气液两相的相互作用来增强雾化和掺混，具有结构简单、供液量大、雾化效果好等优点。国外已在多个型号发动机上使用内混式直流气液喷嘴，但目前关于内混式直流气液喷嘴的研究文献却很少，针对内混式直流气液喷嘴的雾化机理与雾化特性开展研究有重要意义。

在国内公开资料中，杨立军[1]给出了较常用的内混式直流气液喷嘴射流轨迹公式。可知随着液气动量比的增加，内混式直流气液喷嘴中多股射流会发生相撞。国内外学者已对液体射流在横向气流中雾化过程和互击式喷注单元雾化过程进行了大量的研究[2-3]。Pei-Kuan Wu[4-6]研究了射流在横向气流中的雾化过程，重点分析了射流穿透深度和射流角度。Madan Mohan Avulapati[7]对气流辅助互击式喷注单元雾化进行实验研究，分析了液体黏性、液体表面张力、射流撞击角和气流孔直径等参数对雾化特性的影响。Y.Xia[8]采用高速摄影和激光相位多普勒对液气互击式喷注单元雾化过程进行实验研究，分析了雾场粒径分布和液滴速度，为CFD仿真工作提供了参考数据。李佳楠[9]采用相位多普勒分析仪(PDPA)对两股射流撞击雾化特性进行实验研究，重点分析了工质黏性对雾化特性的影响规律。Lai[10]对多种流体进行射流互击实验，分析了射流物性对雾化特性的影响规律。

虽然很多研究者对射流雾化过程和互击式喷注单元进行了大量实验研究，但实验采用的光学设备无法穿透射流柱及浓密的液雾场，只能对雾场宏观特征进行研究，因此很多学者采用数值计算方法对该问题进行研究。仝毅恒[11]采用Euler-Euler 双流体模型的VOF 方法和CLSVOF 方法对射流雾化过程进行数值计算研究，分析了射流破碎形式及其产生的原因，得到CLSVOF方法比VOF方法计算结果准确，这是由于CLSVOF算法同时具有VOF 方法的质量守恒特性与Level Set 方法的精确表面重构特性，计算精度较高。Ehsan Farvardin[12]采用LES结合VOF的方法对横向气流中椭圆形液体射流雾化过程进行数值仿真，得到射流穿透深度、破碎长度、液滴尺寸分布等参数都会随着射流孔形状改变而变化，计算结果表明将LES和VOF方法结合计算精度较高。Heinz Pitsch[13]采用直接数值模拟对射流在气流中一次破碎进行数值仿真，捕捉到了迎风面的表面波，射流轨迹与实验很好的吻合。由于射流雾化过程中形成的液滴数目多且液滴粒径差距大，传统模型中固定的网格量很难满足射流雾化过程中不同位置对空间分辨率的要求。基于Gerris 的树形自适应空间离散算法与分段线性的VOF方法可以很好地解决这一难点，四叉树/八叉树的树形结构网格使得自适应加密算法可简易灵活地实现，网格自适应函数可以用疏密程度不同的网格来解决不同空间对分辨率的需求，在不损失计算精度的情况下显著降低了计算量。李佳楠[14]在国内率先使用Gerris软件对直流互击喷注单元雾化过程进行数值模拟，分析了撞击波的形成机理及孔径比、动量比和射流速度等参数对雾化特性的影响。王凯[15-17]基于Gerris对离心式喷嘴锥形液膜破碎过程进行数值模拟，计算了在不同流量和不同切向孔直径下的液膜锥角、液滴平均粒径SMD 的变化。张波涛[18]采用Gerris开源代码首次对横向气流中射流破碎过程进行数值计算，清晰地捕捉到了射流柱表面形成的表面波，计算得到的射流轨迹、破碎长度和液滴空间分布均与实验结果很好地吻合，全面验证了基于Gerris数值方法计算横向气流中射流雾化过程的高可靠性和高精度性。

本文采用基于Gerris开源代码的自适应加密算法和VOF方法，在国内率先对内混式直流气液喷嘴雾化过程进行研究，分析液气动量比对内混式直流气液喷嘴雾化特性的影响，得到雾场液滴粒径空间分布，为设计内混式直流气液喷嘴奠定了基础。

1 数学物理模型

根据内混式直流气液喷嘴雾化的物理过程，使用八叉树的自适应加密算法对空间进行离散，不可压N-S方程通过有限体积法进行求解，将表面张力转化为某一区域连续的体积力并结合高度函数曲率估计实现表面张力的精确求解，采用单调集成大涡模拟近似模拟亚格子的能量传递[19]。

1.1 控制方程

在计算中假定气液流动过程是等温的且不考虑蒸发过程，因此无需求解能量方程。求解的三维不可压N-S方程组为

(1)

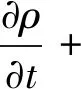
(2)

·u=0

(3)

其中

ρ=p(x,t)

u=(u,v,w)

μ=μ(x,t)

式中：ρ为流体密度；u为流体速度；μ为动力黏度；D为应变张量；δs为集中在界面上的表面张力；κ为界面曲率；n为界面的法向方向。

1.2 VOF方法

采用经典的VOF方法对气液界面进行重构，通过定义第一相体积分数α(x,t)来描述界面。将密度连续方程用体积分数α的连续方程替换为

(4)

采用体积分数定义密度和黏度

ρα=αρ1+(1-α)ρ2

(5)

μα=αμ1+(1-α)μ2

(6)

式中ρ1,ρ2和μ1,μ2分别为第一相与第二相的密度和粘度。

1.3 空间离散

空间离散形式以二维为例进行介绍，通过四叉树网格单元实现，每个正方形单元根据需求都会生产四个子单元，如图1所示。但在网格生成时会有条件限制，直接相邻网格单元的精细化水平相差不能超过1，对角相邻的网格单元的精细化水平相差不能超过1，被固壁切割的相邻网格必须具有相同的精细化水平。

图1 四叉树空间离散例子Fig.1 Example of quadtree mesh discretization

1.4 计算模型与参数设置

内混式直流气液喷嘴结构图如图2所示，喷嘴三维图如图3所示，喷嘴长li=22 mm，轴向气体通道直径为dg=11.25 mm，液体射流孔角度为αl=45°，液体射流孔直径为dl=1.25 mm，液体射流孔距喷嘴出口距离为ll=4.25 mm，液体射流孔数为nl=2。

图2 内混式直流气液喷嘴结构图Fig.2 The structure diagram of internal mixing gas-liquid injector

图3 内混式直流气液喷嘴立体图Fig.3 Stereogram of internal mixing gas-liquid injector

Gerris计算三维算例的空间离散采用八叉树结构形式的立方体网格单元来实现，立方体网格单元如图4所示，称为Box块，每个Box块都可以继续划分生成8个子单元。本文中的计算模型采用38个Box块，如图5所示，通过程序命令喷嘴坐标位置，使喷嘴模型位于左侧2个Box块中，右侧36个Box块组成的立方体为喷嘴外流场。

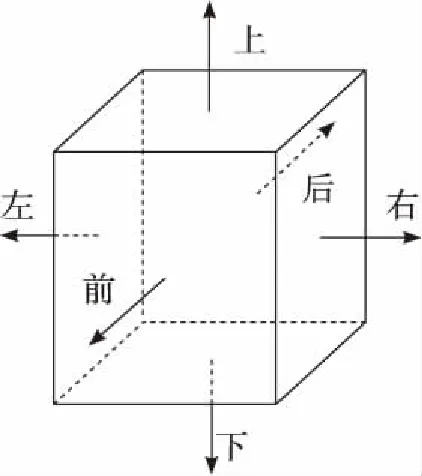
图4 Box块离散方向的定义Fig.4 Definition for discrete direction of Box block

图5 计算域Fig.5 Calculate domain

由于网格为立方体，在计算中发现液体射流圆孔的固体壁面会被立方体网格切分，导致圆形射流孔壁面附近的网格呈锯齿状，壁面附近液体会顺着锯齿状的边界网格形成槽道流动。为解决壁面射流孔附近网格不完整的问题，将Box块的边长设置为略小于气流通道的直径，在射流孔附近用Box块的边逼近圆弧，流体不再从固壁模型中的射流孔喷出，通过程序命令使射流直接从Box块边上射出，这样射流就可以完整射出。在射流后期发展中，射流在混合通道中间运动，不受射流混合通道周边网格被切分的影响。在计算时定义Box块边长为11.1 mm，使用三维建模软件UG建立喷嘴几何模型，将其转换成Gerris能识别的STL格式，再通过stl2gts工具将STL格式文件转成GTS格式文件，最后通过调用Gerris库函数GfsSolid编程写入运算的脚本文件。最高网格加密级别为Level=9级加密，计算的边界条件均按表1进行设置，表1中Vg为气流速度，Vl为液体射流速度，q为液气动量比。液相为水，气相为空气，物性参数如表2所示。

表1 边界条件

表2 物性参数表

2 计算结果与分析

喷嘴雾化实验系统示意如图6所示，实验主要分喷嘴雾化系统和测量拍摄系统。

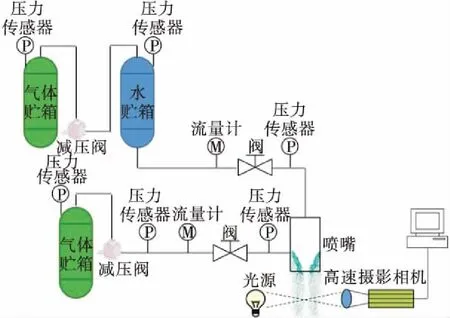
图6 喷嘴雾化实验系统Fig.6 Spray experiment system for injectors

通过雾化系统中的流量计测量喷嘴流量，从而达到流量的精确控制。由于喷嘴不易采用透明材料加工，因此实验只采用高速摄像系统拍摄喷嘴外流场的雾场。图7给出了液气动量比为9.91和47.98的数值仿真结果与实验结果对比图，图7中黑色虚线为喷嘴出口位置。从图7中可以看出数值仿真得到的射流轨迹和射流穿透深度等形态参数与实验拍摄结果基本一致。

图7 不同雾场形态的计算结果与实验结果对比Fig.7 Comparison of spray structure between the simulation results and experimental results

图8为气体速度为68 m/s一定时，射流速度从3 m/s增加到16.5 m/s的雾场分布图和体积分数分布云图，雾场分布图中的颜色代表速度大小。当射流速度为3 m/s时，液气动量比q为1.59，由于射流速度很小，两股液体射流不发生相撞，射流的破碎长度和穿透深度都很小。随着射流速度的增加，轴向气流速度与射流轴向分速度的速度差减小，射流径向速度增大，两股射流柱破碎长度和穿透深度均增大，但射流穿透深度比破碎长度增长快。射流速度为3 m/s和7.5 m/s时的射流雾化过程和雾场形态类似于横向气流中液体射流雾化过程，这时射流只在气动力下发生雾化，雾化机制为气动破碎。当射流速度增大到12.5 m/s时，两股射流发生相撞，其雾场形态有互击式喷注单元雾场形态的特征，但内混式直流气液喷嘴两股射流撞击后形成的液膜在轴向气流的作用下快速破碎，此时雾化机制转变为气动破碎为主，撞击破碎为辅。对雾场信息进行统计，射流速度为16.5 m/s的撞击位置比射流速度为12.5 m/s时的小，但射流速度为16.5 m/s的液膜破碎长度却比12.5 m/s时的液膜破碎长度长，这一规律与互击式喷注单元液膜破碎长度随着液体射流速度增大而减小相反。

图8 不同液气动量比的雾场结构和体积分数分布云图(Vg=68 m/s，改变Vl)Fig.8 Spray structure and volume fraction contours at various liquid-gas momentum ratio(Vg =68 m/s, Vl is changed)

这是由于互击式喷注单元随着射流速度的增加，射流动量增大，即轴向分量与径向分量同时增加，导致撞击波波动幅值增大，波长减小，液膜破碎长度也减小。但内混式直流气液喷嘴比互击式喷注单元多了轴向气流，随着射流速度的增加，虽然撞击波波动幅值变大，但由于轴向气流速度与射流柱轴向分速度差减小，其液膜受到的气动力相对减小，液膜破碎长度反而增长，因此对于内混式直流气液喷嘴，气动破碎比撞击破碎对液膜破碎长度影响更大。

图9是液体射流速度为12.5 m/s一定时，轴向气流速度从51.5 m/s增加到82 m/s的雾场分布图和体积分数分布云图。随着轴向气流速度增加，即液气动量比q减小，射流柱在轴向气流的作用下弯曲程度逐渐变大，两股射流柱的撞击位置向右偏移。射流柱表面有液滴剥离且贯穿于射流发展全过程，两股射流柱撞击后形成的液膜在轴向气流的作用下破碎距离明显减小。

图9 不同液气动量比的雾场结构和体积分数分布云图(Vl=12.5 m/s，改变Vg)Fig.9 Spray structure and volume fraction contours at various liquid-gas momentum ratio(Vl =12.5 m/s, Vg is changed)

这时雾化机制是气动破碎为主，撞击破碎为辅。当轴向气流速度增大到75 m/s时，可以发现两股射流柱在撞击前已经断裂，断裂后形成的小液块在惯性力和气动力的共同作用下运动发生相撞。当气流速度为82 m/s时，两股射流柱不发生相撞。因此液气动量比q是影响喷嘴雾化最重要的工作参数，在本文的喷嘴模型中，随着q的增加，喷嘴雾化过程由两股射流柱不相撞模式转变为相撞模式，其临界点为q=22左右。

图10和图11分别对比了不同工况下的射流穿透深度和破碎长度，图10(a)和图11(a)中横向气流速度均为68 m/s，射流速度分别为3 m/s，7.5 m/s，12.5 m/s，16.5 m/s，从图10(a)和图11(a)中可以看出射流穿透深度和破碎长度均随着射流速度增加而增大。图10(b)和图11(b)中射流速度均为12.5 m/s，横向气流速度分别为51.5 m/s，75 m/s，82 m/s，从图10(b)和图11(b)中可以看出射流穿透深度和破碎长度随着横向气流速度增加而减小，因此可以得到射流穿透深度和破碎长度均随着液气动量比增加而增大。

图10 不同工况的射流穿透深度Fig.10 The jet penetration depth at various cases

Gerris可以对全场液滴的数目和体积进行统计后并输出。图12为不同工况时的液滴SMD，图12(a)中轴向气流速度为68 m/s时，随着液体射流速度从3 m/s增加到16.5 m/s，液气动量比增加，液滴SMD有增大的趋势，图12(b)中液体射流速度为12.5 m/s时，随着轴向气流速度从51.5 m/s增加到82 m/s，液气动量比减小，液滴SMD有减小的趋势。内混式直流气液喷嘴全场液滴SMD为50～60 μm，液滴SMD随着液气动量比增加而增大。文献[6]中互击式喷注单元液滴SMD为150 μm左右，约为内混式直流气液喷嘴液滴SMD的3倍，因此轴向气流速度对内混式直流气液喷嘴雾化特性影响很大。

图11 不同工况的射流破碎长度Fig.11 The jet breakup length at various cases

3 结论

通过对内混式直流气液喷嘴雾化过程开展数值模拟工作，得出的主要结论如下:

1)通过采用基于Gerris开源代码的VOF方法和树形自适应加密算法对内混式直流气液喷嘴进行数值模拟，可以详细展现雾化过程，并捕捉到雾场细节特征。

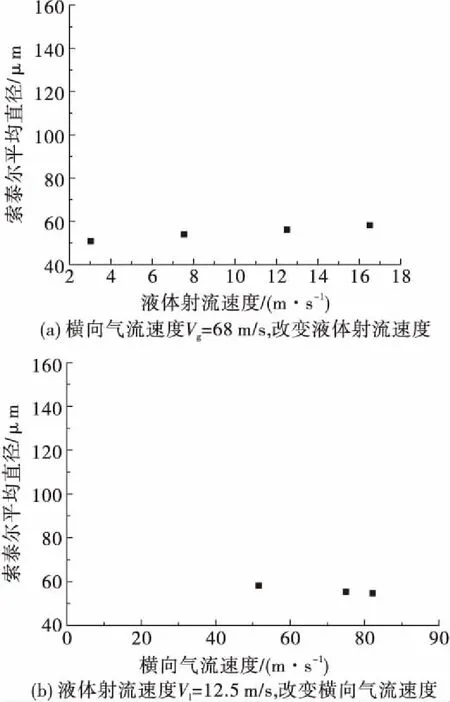
图12 不同工况的液滴SMD Fig.12 Droplet SMD at various cases

2)液气动量比是影响内混式直流气液喷嘴雾化特性的重要工作参数，随着液气动量比增加，两股射流柱穿透深度和破碎长度均增大。当液气动量比增大到22左右时，射流柱会发生相撞，其雾化机制由气动破碎转变为气动破碎为主、撞击破碎为辅。

3)当射流柱相撞时，轴向气流速度与射流轴向分速度差是影响液膜破碎长度的重要参数，液膜破碎长度随着轴向气流速度与射流轴向分速度差的增大而减小。

4)内混式直流气液喷嘴全场液滴平均粒径SMD为50～60 μm，液滴SMD随着液气动量比的增加而增大。