一种自适应变异策略的集体决策优化算法

(长江大学信息与数学学院，湖北 荆州 434023)

随着计算机的不断发展，人们提出了越来越多的元启发式算法，并广泛地运用到复杂的函数优化问题上。这些元启发式算法大致可以分为基于进化的元启发式算法、基于物理的元启发式算法和基于群体的元启发式算法3类。常见的基于进化的元启发式算法有遗传算法(GA)[1]、差分进化算法(DE)[2]、回溯搜索优化算法(BSA)[3]，基于物理的元启发式算法有模拟退火算法(SA)[4]、黑洞算法(BH)[5]、引力搜索算法(GSA)[6]，基于群体的元启发式算法有蚁群优化算法(ACO)[7]、粒子群优化算法(PSO)[8]、人工蜂群优化算法(ABC)[9]。随着对算法的进一步研究，人们提出了很多改进的策略来增强算法的性能，包括改进的自适应差分进化算法(ADE)[10]、自适应变异尺度系数和混合选择的回溯搜索算法(FS-BSA)[11]、基于多变异策略的自适应差分进化算法(ADE-MM)[12]。这些算法基本上都是在收敛速度和全局搜索能力之间做出改进。

集体决策优化算法(CDOA)是张清华博士于2016年受到集体决策行为启发提出的一种基于种群的进化算法[13]。每个决策者相当于每次迭代的个体，决策者之间进行交流最终产生的方案就相当于最优解。CDOA共有5步变异策略，分别是个体最优、较好的其他个体、种群重心、全局最优学习以及对局部最优个体的变异，这些策略加快了算法的收敛速度，但种群多样性不够，并且算法在每一次迭代过程中需要5次函数评价，大大增加计算成本。

针对CDOA的不足，笔者提出了一种自适应变异策略的集体决策优化算法(ACDOA)，在变异策略中以一种自适应的概率在增大种群多样性和加快收敛速度的这2个变异算子中选择1个作为变异算子对每一个个体进行变异。在当前种群中2种变异策略被选择的概率与上一代种群中2种变异策略的成功率成正比，并随2种变异策略搜索最优解自适应的改变。若前一种策略变异后个体适应度大的个体越多，则下一次迭代选择该策略的概率越大；反之，选择后一种变异策略的概率越大。

1 集体决策优化算法

集体决策优化算法是基于种群的进化算法，与其他进化算法类似，算法分为变异、选择2个部分。

随机产生种群pop和第t次迭代的个体：

(1)

式中：i=1,2,…,N，N为种群大小；D为种群维数；lxk、uxk分别表示第k代个体的下界和上界；U表示均匀分布。

1.1 变异

1.1.1 经验阶段

该阶段是依据会议中领导的经验做出的决策。CDOA算法根据种群中每个个体适应值选出相应的最好的个体(Xb)来设计的算子，具体如下：

(2)

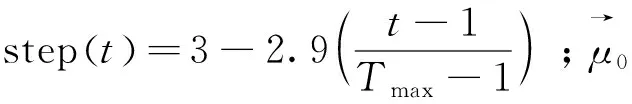
1.1.2 交流阶段

接下来，所有的决策者随意的相互交流意见。在算法中表现为随机选取一个比当前代个体Xi(t)适应度大的个体Xj(t)指导个体学习，算子如下：

(3)

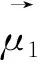
1.1.3 群体思考阶段

群体思考会影响每个决策者进行决策，相应的选取所有个体的重心(XG)：

(4)

向群体学习的算子如下：

(5)

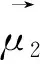
1.1.4 领导阶段

领导的决策不仅影响其他的决策者，并且决定着会议的方向和最终的方案。相应的选取种群中最好的个体XL，算子如下：

(6)

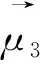
然而，领导的决策只能改变自己。因此，在算法中笔者运用随意扰动策略来轻微地改变个体XL，也就是局部搜索：

(7)

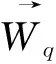
XL=newXkk=min_ObjFun(newXq)

(8)

其中：min_ObjFun是最小目标函数值的指标。

1.1.5 创新阶段

在决策过程中，创新对产生一个好想法起到了一定的作用。为了避免局部最优，CDOA利用创新对变量进行细微变异增大种群的多样性，其类似于其他进化算法里的交叉算子。相应算子如下：

(9)

式中：r0是区间(0, 1)上的一个随机数；p是区间[1,D]内的随机整数；MR是创新因子，是一个常数。

1.2 选择

CDOA的选择是将得到的5个子代个体newXi0、newXi1、newXi2、newXi3、newXi4和1个父代个体Xi进行比较，保留适应度高的个体进入下一代。

最后将得到的新种群pop放入下一代循环，并重复上述过程，直到满足循环终止条件为止。

2 ACDOA

CDOA的变异算子运用了个体最优、全局最优、重心等个体指导变异。这种方式加快了算法的收敛速度，但是前期种群的多样性不够，容易使算法陷入局部最优，且任意组合CDOA中的几个变异算子可以形成一个新的算法。笔者提出了自适应变异策略，在原算法中选出2组变异算子，前一种在迭代前期增强种群的多样性，后一种变异算子在迭代后期加快收敛速度，算子如下：

(10)

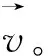
(11)

式(11)表示通过向其他个体学习变异策略变异后和向领导者学习变异策略变异后能成功进入下一代的子代个体占父代个体的比例。因此，在变异过程中使用这2种变异策略的概率是不断进行更新的，即种群自适应的选择变异策略进行变异。一旦在前期种群陷入局部最优，ns1、ns2、nf1、nf2参数会被重置。这种不断自适应的过程会让算法在进化过程中选择最适合的学习策略。

算法计算步骤如下:

1)初始化操作：随机产生N个个体的初始的种群，即pop(t)={X1(t) ,…,Xi(t),…,XN(t)}确定最大进化代数Tmax，令T=0，初始概率p=0.5。

2)对第T代个体Xi(t)执行式(2)～式(10)步骤生成第T+1代个体。

3)记录ns1，ns2，nf1，nf2的大小，代入式(11)计算出p的值，然后将生成的T+1代个体根据前面计算p的值代入式(10)进行计算。

4)选择：将生成的 newXi0，newXi2子代个体与Xi(t)父代个体比较保留适应度高的个体。

5)t=t+1。

6)重复步骤2)～ 步骤6)，直到求得最优解或T>Tmax。

3 算法测试

利用3个标准的测试函数Spere、Ackley、Schwefel测试ACDOA的有效性，并将得到结果与CDOA的结果进行比较。测试函数如表1所示，测试结果如表2所示，每一次的迭代结果收敛图如图1所示。算法参数如下：种群大小N=50，最大迭代次数T=6000。

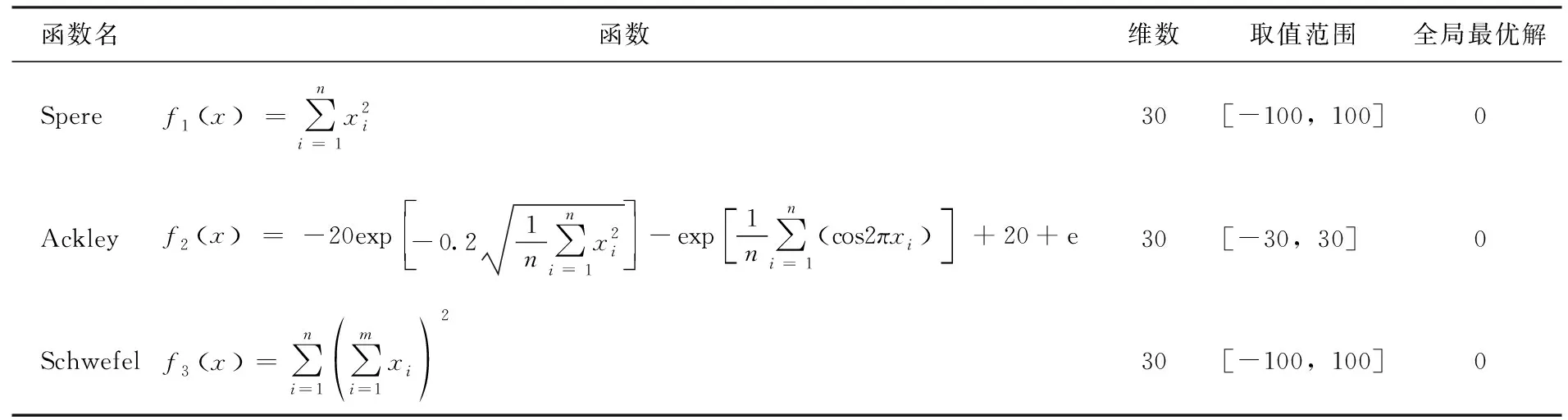
表1 测试函数及参数设定

表2 算法寻优结果

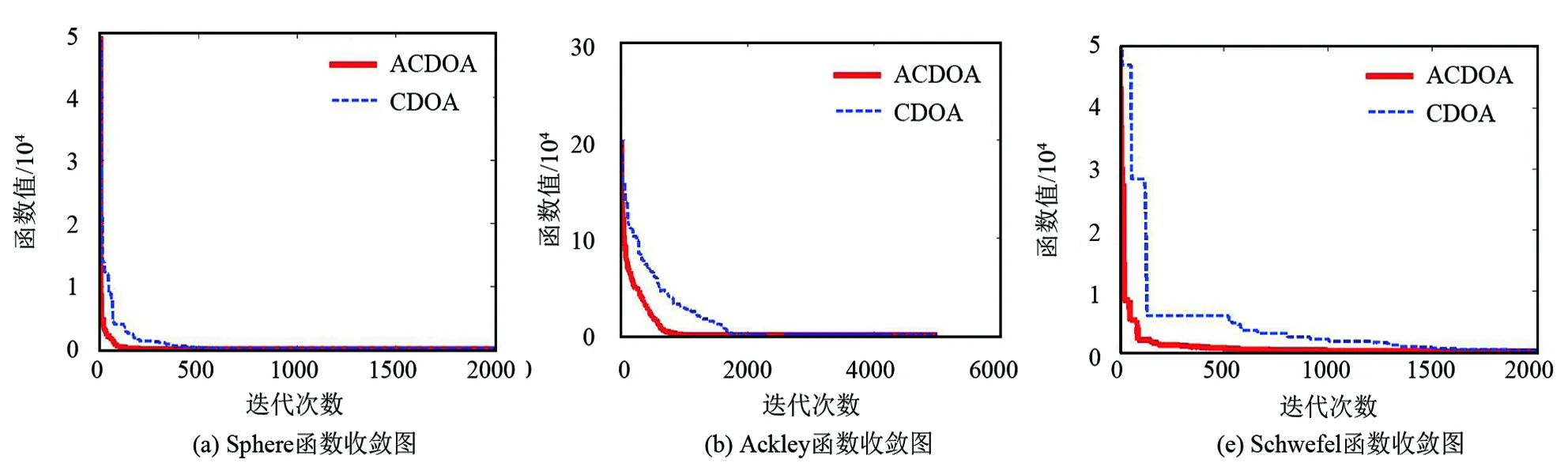
图1 3个函数收敛图

表1中，Sphere函数为单峰函数，不存在局部最优解；其余函数均为多峰函数，存在较多局部最优解；3个函数的最优值均在零点处。表2中，通过3个函数寻优的结果可以看出，ACDOA和CDOA都能找到最优值，且ACDOA找到的最优值更接近函数的最小值，说明ACDOA在收敛精度上较CDOA有较大的提升，并且具有良好的竞争力。从图1还可以看出，ACDOA(红色)的收敛速度在3个函数中都好于CDOA(蓝色)。综上所述，ACODA在寻优准确率和寻优精度上较CODA都有进一步的提高。

4 结语

为提高CDOA算法的搜索效率，提出了一种自适应变异策略的集体决策优化算法(ACDOA)。算法的设计思想是使算法在保持收敛速度快的基础上增强全局搜索能力。3个测试函数的测试结果表明，ACDOA较CDOA具有更快的收敛速度、更高的收敛精度以及更好的全局收敛能力，说明了ACDOA的可行性和有效性。