畜产品供应链质量控制策略的微分博弈分析*

安玉莲，孙世民，夏兆敏

(1.山东农业大学经济管理学院，泰安 271018；2.山东财经大学工商管理学院，济南 250014)

0 引言

中国是世界上最大的畜产品生产和消费国，2015年全国肉、蛋、奶总产量分别达到8 625万t、2 999.2万t和3 870.3万t，对于改善城乡居民的饮食结构和生活质量发挥了重要作用。但是，近年来中国畜产品质量安全隐患普遍存在，既有消费者难以观察到的有毒有害物质残留超标问题，又有“瘦肉精”和“三聚氰胺”为代表的畜产品质量安全事件，严重影响了消费者的身心健康和中国畜产品国际竞争力的培育与提升。导致中国畜产品质量安全问题的原因很多，但畜产品供应链节点企业(包括养殖场户、屠宰加工企业和超市，下同)的质量预防水平和质量检验水平不合理且相互间协同程度不高是深层次的根源因素。因此，科学制定畜产品供应链质量控制策略，实现节点企业之间的质量协同控制，是解决中国畜产品质量安全问题的客观要求，迫切需要深入研究。

21世纪以来，国内外学者运用质量管理、博弈论、控制论、委托代理、供应链优化等理论、方法和技术，对供应链质量控制问题开展了许多研究。国外代表性研究有，Baiman[1]等建立了供应商质量预防和制造商质量评价基本模型，并且综合考虑供应商的逆向选择和制造商的道德风险而建立了产品质量决策控制模型，制定了产品质量控制策略。Balachandran[2]等研究了单边和双边道德风险下通过检验和外部损失信息确定对供应商质量缺陷的惩罚，从而进行供应商质量决策。Cachon[3]等通过设计需求预测分享和收益分享契约，以解决非对称信息条件下供应链质量协同控制的决策问题。Thomas[4]设计了一个由供应商和制造商组成的二级供应链质量预防和质量控制的合作方法。国内代表性研究有，张翠华等[5]运用委托代理模型，研究了质量检验制度下供应商质量努力、自身检验水平信息隐匿以及两者都隐匿时供应链协同质量控制问题。尤建新等[6]基于委托代理理论，研究了供应商质量预防水平隐匿、购买商质量检验水平隐匿以及两者均隐匿3种道德风险条件下的供应链质量合同设计与质量控制策略。洪江涛等[7]应用微分博弈方法研究了两级供应链中供应商和制造商的质量控制协调问题。朱立龙等[8]基于动态博弈分析构建了质量控制模型，研究了创新驱动条件下三级供应链分销渠道产品质量控制策略。姜德金等[9]利用博弈方法，分析了销售商检测水平有限和制造商分担外部损失条件下供应链质量控制的互动协调策略。近年来，国内一些学者开始借鉴一般供应链质量控制的研究成果，运用博弈分析方法，探讨以乳品和猪肉为代表的畜产品供应链质量控制问题(尹巍巍等[10]；申强等[11]；夏兆敏等[12]；张园园等[13])。供应链环境下，畜禽养殖与屠宰加工是影响畜产品质量安全水平的两个关键环节，在此期间畜产品质量形成过程具有明显的动态性、连续性和长期性(如从母猪怀孕到分娩再到生猪育肥、屠宰、猪肉上市，需要300d左右的时间)，因此在动态框架下研究畜产品质量控制策略更加贴近现实，并且畜禽养殖环节的质量预防、屠宰加工环节的质量检验和质量预防对于畜产品质量既独立发挥作用又协同互动。但是，现有研究对这些问题涉及较少。

文章将在借鉴已有研究成果的基础上，首先考虑养殖场户的质量预防水平、屠宰加工企业的质量检验水平和质量预防水平，构建描述畜产品质量变化的微分方程；再考虑质量控制收益及其分配和质量控制成本及其分摊，构建畜产品供应链质量控制微分博弈模型，确定不同博弈模式下养殖场户和屠宰加工企业的质量控制策略及其协同条件；最后通过数值模拟验证所建模型的科学性和研究结论的正确性。

1 问题描述与假设

由于养殖与屠宰加工是影响畜产品质量的两个关键环节，因此该文重点研究畜产品供应链中养殖场户和屠宰加工企业之间的质量控制策略及其协同问题。畜产品供应链运行过程中，养殖场户按照质量合格畜禽的标准和要求，在环境维护、投入品采购、疫病防控、设施配置、养殖档案、动物福利及其与屠宰加工企业协同合作等方面采取质量预防措施；屠宰加工企业首先对养殖场户提供的畜禽进行毛色、步态、呼吸和体温等外在质量检验，以及疫病、兽药残留量和有毒有害物质含量等内在质量检验，然后按照畜禽屠宰加工工艺流程的标准和要求，在环境维护、设施配置、生产档案、动物福利、储存保鲜及其与养殖场户协同合作等方面采取质量预防措施。借鉴已有研究成果，该文进行如下基本假设。

①养殖场户和屠宰加工企业都是经济人假设条件下的理性个体，双方均完全了解对方的成本和收益信息。

②畜产品供应链提供给市场的畜产品质量由养殖场户的质量预防水平、屠宰加工企业的质量检验水平和质量预防水平共同决定，且随时间而动态变化。借鉴洪江涛等[7]和夏兆敏等[12]关于“供应链产品质量动态演变”的思想并进一步扩展，将畜产品供应链中畜产品质量随时间变化的规律表达微分方程为：

(1)

式(1)中，表Q(t)示畜产品质量在t时刻的质量，Q(0)=Q0为质量初始值；x(t)∈[0，1]表示养殖场户在t时刻的质量预防水平，即养殖出质量合格畜禽的概率；y(t)∈[0，1]表示屠宰加工企业在t时刻的质量检验水平，即将质量不合格畜产品检验出来的概率；α、β、γ和δ均为大于零的常数，分别表示养殖场户质量预防水平、屠宰加工企业质量检验水平和屠宰加工企业质量预防水平对畜产品质量的影响系数(统称质量控制效果系数)，以及畜产品质量的相对衰减率。

③为避免价格竞争对该文主题(畜产供应链质量控制策略)的干扰，假定畜产品价格为常数。参照洪江涛等[7]和夏兆敏等[12]关于“市场需求、产品质量与供应链总收益间关系”的假设，用线性函数描述畜产品供应链总收益π(Q(t))与畜产品质量间得的关系为：

π(Q(t))=m+nQ(t)

(2)

式(2)中，m和n均为大于零的常数，n为畜产品质量对畜产品供应链总收益的影响程度。

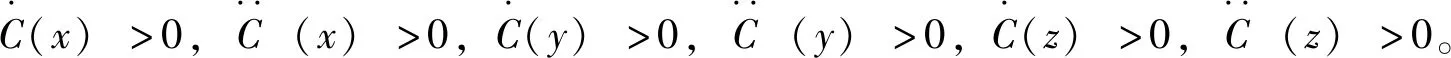
⑤养殖场户和屠宰加工企业共同分享畜产品供应链总收益，其中养殖场户分得总收益的比例为σ，屠宰加工企业为1-σ，σ∈(0，1)称为收益分配系数。

⑥养殖场户和屠宰加工企业有相同且大于零的贴现率ρ，双方的目标都是在无限时区内寻求能够实现自身收益最大化的最优质量控制策略。

2 质量控制的微分博弈模型构建与分析

该文将分“双方独立平等的Nash非合作博弈”、“屠宰加工企业主导的Stackelberg主从博弈”和“双方协同合作博弈”3种情况，构建畜产品供应链质量控制的微分博弈模型并对模型结果进行比较分析。

2.1 Nash非合作微分博弈模型

在Nash非合作博弈模式下，养殖场户和屠宰加工企业的关系平等系，双方同时、独立地选择各自的最优质量控制策略，以实现自身收益最大化。则，养殖场户的目标函数为：

(3)

屠宰加工企业的目标函数为：

(4)

养殖场户和屠宰加工企业的质量控制策略是当前状态变量畜产品质量和时间的函数。由于该文所建模型中的所有参数都是与时间无关的常数，且在无限时区的任何时段内养殖场户和屠宰加工企业实际上面对的是相同的博弈，因而双方的最优质量控制策略组合为静态反馈Nash 均衡。为书写方便起见，下文将省略时间t。

根据静态反馈Nash均衡的充分条件，养殖场户的最优值函数Vf和屠宰加工企业{的最优值函数Vs均是有界、连续、可微的，两者必须满足如下汉密尔顿—雅可比—贝尔曼(Hamilton-Jacobi-Bellman)方程[14]，简称HJB方程。

(5)

(6)

基于已有研究文献(洪江涛等[7]；夏兆敏等[12])，该文总结出上述HJB方程的“五步求解法”。

第一步，由式(5)和式(6)右边最大化的一阶偏导数条件得：

(7)

第二步，将式(7)分别代入式(5)和式(6)进行合并整理为：

(8)

(9)

由式(8)和式(9)可见，关于Q的线性最优值函数是式(5)和式(6)对应的HJB方程的解，于是令：

Vf=g1+h1Q，Vs=u1+w1Q

(10)

其中，g1、h1、u1、w1为待定常数。将式(10)及其对Q的导数分别代入式(8)和式(9)。

第三步，利用待定系数法进行求解得，

(11)

由式(11)可见，养殖场户和屠宰加工企业的质量控制策略与畜产品供应链总收益分配系数σ有关。其中，养殖场户的质量预防水平与σ成正比，而屠宰加工企业的质量检验水平和质量预防水平均与σ成反比。因此，要不断改善畜产品质量，就应确定合理的畜产品供应链总收益分配系数σ，实现养殖场户和屠宰加工企业质量控制策略的最佳组合。

第五步，将g1、h1、u1、w1代入式(10)得到养殖场户、屠宰加工企业和畜产品供应链的最优值函数为：

(12)

2.2 Stackelberg主从微分博弈模型

在Stackelberg主从博弈模式下，作为畜产品供应链的核心企业，屠宰加工企业在质量控制过程中充当领导者角色，并主动分担养殖场户的质量预防成本，养殖场户是质量控制的跟随着，双方质量控制策略的决策是一个序贯非合作博弈过程。屠宰加工企业首先确定最优的质量检验水平、质量预防水平和养殖场户质量预防成本分担比例τ∈[0，1]；养殖场户在观察到屠宰加工企业的决策后再决定自己的最优质量预防水平；屠宰加工企业在做出决策前能够预料到养殖场户的跟随反应。此时，养殖场户和屠宰加工企业的最优质量控制策略组合为静态反馈Stackelberg均衡。

运用逆向归纳法，首先确定养殖场户的最优质量预防水平。养殖场户的目标函数为：

(13)

养殖场户作为Stackelberg博弈的跟随者，其最优质量预防水平的确定是一个单方最优化控制问题。根据静态反馈Stackelberg均衡条件和最优控制原理，养殖场户的最优值函数Vf必须满足如下HJB方程：

(14)

(15)

式(15)的最优值函数Vs必须满足如下HJB 方程：

(16)

针对式(14)和式(16)对应的HJB方程，利用“五步求解法”，得到Stackelberg主从博弈模式下，养殖场户和屠宰加工企业的最优质量控制策略：

(17)

其他

(18)

由式(17)可见，在收益分配系数σ∈(0，2/3)范围内，τ**∝1/σ。这表明，养殖场户分得的畜产品供应链总收益比例越高，屠宰加工企业为其分担的质量预防成本比例越低。这体现了畜产品供应链运作过程中，养殖场户和屠宰加工企业之间利益分配与成本分摊的互动协调关系。

最优控制策略条件下，养殖场户、屠宰加工企业和畜产品供应链的最优值函数为：

(19)

2.3 协同合作微分博弈模型

在协同合作博弈模式下，养殖场户和屠宰加工企业成为一个整体，双方以畜产品供应链总收益最大化为目标，共同确定各自的最优质量控制策略。则，畜产品供应链的目标函数为：

(20)

式(20)的最优值函数V必须满足如下HJB方程：

(21)

利用“五步求解法”得到协同合作博弈模式下，养殖场户和屠宰加工企业的最优质量控制策略：

(22)

在协同合作博弈模式下，养殖场户和屠宰加工企业按照σ和1-σ的比例分配畜产品供应链总体收益。因此有：

(23)

2.4 比较分析

根据式(11)、式(18)和式(22)以及式(12)、式(19)和式(23)得出养殖场户和屠宰加工企业间由Nash非合作博弈→Stackelberg主从博弈→协同合作博弈时，质量控制策略的调整量与最优值函数的增量，详见表1(计算过程略)。

表1 非合作博弈、主从博弈、协同合作博弈的质量控制水平与最优值函数比较

表1中，Δx、Δy、Δz、ΔVf、ΔVs和ΔV分别表示不同博弈模式下，养殖场户质量预防水平、屠宰加工企业质量检验水平、屠宰加工企业质量预防水平、养殖场户最优值函数、屠宰加工企业最优值函数和畜产品供应链最优值函数等项指标的增量。由表1得出如下命题：

命题1 若畜产品供应链总收益分配系数σ∈(0，2/3)则养殖场户与屠宰加工企业间的Stackelberg主从博弈严格优于双方间的Nash非合作博弈。具体表现为，当双方由Nash非合作博过渡到Stackelberg主从博弈时，养殖场户的质量预防水平提高，屠宰加工企业的质量控制水平不变，养殖场户、屠宰加工企业和畜产品供应链的最优值函数均增加。

命题2 养殖场户与屠宰加工企业间的协同合作博弈整体上优于Stackelberg主从博弈。具体表现为，双方由Stackelberg主从博弈过渡到协同合作博弈时质量控制水平均提高，畜产品供应链的最优值函数增加。

命题3养殖场户与屠宰加工企业间的协同合作博弈是一种集体理性模式。具体表现为，协同合作博弈模式下，养殖场户和屠宰加工企业的质量控制水平与畜产品供应链的最优值函数均大于分散博弈模式下的质量控制水平与最优值函数。

3 畜产品供应链质量控制策略的协同机制

命题3表明，养殖场户与屠宰加工企业间的协同合作博弈是保障畜产品质量的充要条件。根据制度经济学的基本原理，只有通过设计合理的畜产品供应链总收益分配制度，才能在满足个体理性的前提下实现集体理性。即，确定合理的畜产品供应链总收益分配系数σ，确保对于养殖场户和屠宰加工企业的收益来说协同合作博弈是Pareto最优的，双方才能开展质量协同控制，畜产品质量得以不断改善。

3.1 质量控制策略的协同条件

根据表1，养殖场户和屠宰加工企业的个体理性条件为：

(24)

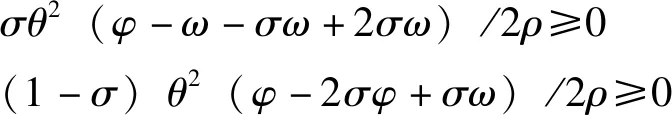
(25)

由式(24)得：

2ω/(φ+4ω)≤σ≤4ω/(φ+4ω)

(26)

由式(25)可得：

(ω-φ)/(2ω-φ)≤σ≤φ/(2φ-ω)

(27)

综合式(26)和式(27)得：

max{2ω/(φ+4ω)，(ω-φ)/(2ω-φ)}≤σ≤min{4ω/(φ+4ω)，φ/(2φ-ω)}

(28)

命题4 当且仅当畜产品供应链总收益分配系数满足式(28)时，养殖场户与屠宰加工企业才能实现质量协同控制。

由式(28)可见，在质量协同控制模式下，畜产品供应链收益分配系数区间的左右端点与φ成反比，φ变大时区间左移，养殖场户分享供应链收益减少；与ω成正比，ω变大时区间右移，养殖场户分享供应链收益增加。这是因为，φ越大，说明养殖场户的质量控制越容易，因而其分享的供应链收益越少；ω越大，说明屠宰加工企业的质量控制越容易，因而其分享的供应链收益越少，养殖场户分享越多。这也体现了畜产品供应链运作过程中，质量控制收益分配与质量控制难易程度之间的互动协调关系。

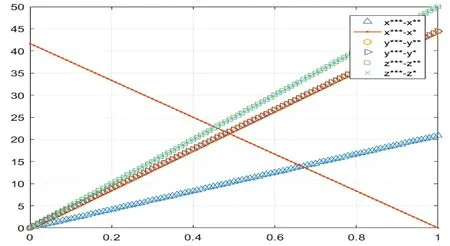
图1 Δx、Δy、Δz随σ变化的曲线

3.2 数值模拟

为直观验证所建模型及命题(因篇幅所限，仅验证命题3和命题4)的正确性，假定模型中的常量参数为：α=2.5，β=2，γ=1.5；k=0.8，λ=0.6，μ=0.4，ρ=0.1，则有：θ=13.333，φ=7.812 5，ω=12.291 7，2ω/(φ+4ω)=0.431 4，4ω/(φ+4ω)=0.862 8，(ω-φ)/(2ω-φ)=0.267 1，φ/(2φ+ω)=2.343 8。(超出σ的取值范围，舍去。)结合式(11)式(18)和式(22)以及式(12)式(19)和式(23)将θ、φ和ω的值代入表1中的相关项，利用Matlab7.11.0进行数据模拟仿真，得出图1、图2和图3所示的不同博弈模式下，质量控制水平增量、畜产品供应链最优值增量，以及养殖场户和屠宰加工企业最优值函数增量随畜产品供应链总收益分配系数变化的曲线。

图2 ΔV随σ变化的曲线 图3 ΔVs、ΔVf随σ变化的曲线

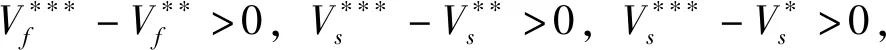
4 结语

该文运用微分博弈方法，导出了Nash非合作博弈、Stackelberg主从博弈和协同合作博弈3种模式下，畜产品供应链中养殖场户和屠宰加工企业的最优质量控制策略与最优值函数，分析了实现养殖场户和屠宰加工企业质量协同控制的畜产品供应链总收益分配机制。结果表明养殖场户和屠宰加工企业之间协同合作时，个体收益和供应链总体收益都是最优的，并通过数值模拟验证了所建模型与结论的正确性。主要结论包括：(1)若畜产品供应链总收益分配系数σ∈(0，2/3)则养殖场户与屠宰加工企业间的Stackelberg主从博弈严格优于双方间的Nash非合作博弈。(2)养殖场户与屠宰加工企业间的协同合作博弈整体上优于Stackelberg主从博弈。具体表现为，双方由Stackelberg主从博弈过渡到协同合作博弈时质量控制水平均提高，畜产品供应链的最优值函数增加。(3)养殖场户与屠宰加工企业间的协同合作博弈是一种集体理性模式。协同合作博弈模式下，养殖场户和屠宰加工企业的质量控制水平与畜产品供应链的最优值函数均大于分散博弈模式下的质量控制水平与最优值函数。(4)在质量协同控制模式下，畜产品供应链收益分配系数区间与φ成反比，φ变大时区间左移，养殖场户分享供应链收益减少；与ω成正比，ω变大时区间右移，养殖场户分享供应链收益增加。这是因为，φ越大，说明养殖场户的质量控制越容易，因而其分享的供应链收益越少；ω越大，说明屠宰加工企业的质量控制越容易，因而其分享的供应链收益越少，养殖场户分享越多。