悬臂静子间隙影响的计算分析

张明华*

（中国商用飞机有限责任公司，上海200126）

0 引言

轴流压气机自诞生以来，随着设计技术的不断进步，其级压比不断提高[1]。在保持反力度基本不变的前提下，静子的负荷必然相应明显提高，而静子的负荷往往受限于静子根部的角区失速的发生。

早在1954年，Dean[2]就指出，端壁附面层内的低能流体在横向二次流作用下，向吸力面角区堆积，角区低能流体在流向逆压梯度作用下，容易发生分离，这样的分离形式称为三维角区分离。三维角区分离是压气机端区固有的二次流动，在大流量状态或者设计状态，静子端区的角区分离处于一种弱分离形式，端壁并不存在明显回流区，对流动并不会造成明显的堵塞和损失；随着来流攻角的增大，静子端区可能发展成为一种强分离形式，端壁区存在大的回流区，并对叶片通道内的流动造成大的流动损失和堵塞。Lei[3][4]将这两种形式的分离称为角区分离和角区失速，而Taylor[5]则将其称为闭式分离和开式分离，这里采用Lei的分类。当角区失速发生时，压气机的压升和效率会出现显著下降，在压气机的整个工作范围内，应该尽量避免角区失速的发生[6]-[9]。大量的研究表明，悬臂静子根部的间隙泄漏流能够有效的控制三维角区分离。

Dean[2]指出叶尖泄漏流和端壁横向二次流在周向的流向相反，泄漏流能够抑制横向二次流对端壁附面层内低能流体的输运作用，从而起到控制三维角区分离的效果。后来，Lakshminarayana[10]-[12]进行了大量的平面叶栅实验，证实了这一结论的正确性，并指出存在一个使得叶栅损失最小的最佳间隙。最佳间隙对应于叶尖间隙的大小正好使得泄漏流与端壁横向二次流的强度基本一致，角区分离得以完全吹除的状态。随后，诸多学者通过数值模拟或实验的方式证实了静子叶栅中最佳间隙的存在[6]，[13]-[19]，但得到的最佳间隙差异较大（Chen[19]-1%弦长，Gbadebo[15]-0.58%弦长，韩少斌[16]-0.5%弦长，王子楠[17-18]-0.7%弦长）。在叶轮机中，Dong[20]也发现悬臂静子的间隙泄漏流能够有效的控制静子根部的角区分离，压气机特性得以改善。后来，在不同压气机中都观察到了这一现象[21]-[24]。George[25]对一个高负荷压气机进行数值模拟，得到压气机特性最优的静子间隙约为1%叶高。Wennerstrom[26]和 Mcdougall[27]指出压气机转子叶尖间隙同样存在最佳间隙，大约为0.5%～1%弦长。不过Sakulkaew[28]指出转子中最佳间隙的存在主要是因为，叶尖间隙较小时，间隙内的粘性损失随着间隙减小而增大，而泄漏流与主流的掺混损失随之减小。

可见，在不同形式的压气机或者叶栅中，最佳间隙的数值相差很大，对最佳间隙的影响因素的研究很少。本文在压气机级环境下，采用CFD计算，开展高负荷悬臂静子间隙影响的研究。分别计算了常规负荷和高负荷、小轮毂比和中等轮毂比几种组合方案，以研究压气机负荷水平和轮毂比的影响。

1 计算设置及校验

考虑到在压气机级环境中，流动的三维性与非定常性很强，且同时存在泄漏流与角区分离等复杂的流动结构，为此首先利用某低速压气机的实验结果对所用的CFD软件及计算设置进行了校验。限于实验结果，且考虑到角区分离为本文的主要研究对象以及计算难点，此处只对静子根部无间隙时，静子轮毂的角区分离进行校核。

1.1 计算软件校验

本文采用AutoGrid5进行网格划分，进口导叶网格总数为1 000 203，转子网格总数为1 195 741，静子网格总数分别为1613879；使用CFX15.0软件进行数值计算，采用高精度数值计算格式，k-ω湍流模型。经过计算发现，这样的设置条件，基本能保证壁面的Y+都小于2，并且能满足网格无关性要求。

为了对计算结果进行校验，采用叶片表面以及轮毂和机匣壁面的油流显示结果来进行对比分析。图1分别给出了设计点（DE）和近失速点（NS）在静子吸力面和轮毂的油流实验结果和CFX计算的壁面流线，机匣上面的壁面流线并没有显示出明显的流动结构，在此没有给出。通过油流的结果发现，在设计点时，静子吸力面的根尖都出现了较小尺度的分离区，而轮毂和机匣壁面都看不到明显的分离结构，说明分离只局限在叶片吸力面。在近失速点时，叶根的角区分离发展为角区失速，分离区明显扩大，在吸力面和轮毂壁面流线上显示出大的回流区。而计算的结果无论在分离结构还是分离尺度上，都与油流显示的结果基本相符，因此可以认为在这样的设置条件下，CFX能很好的模拟出静子在各个不同状态时的分离结构与分离区大小。

图1 实验与计算的壁面极限流线对比

1.2 计算方案

本文利用校验后的CFD计算方案，首先计算分析了进行过实验的单级小轮毂比高负荷压气机，其轮毂比为0.6，设计点叶中截面D因子为0.48，转静子均采用C4叶型，为了分析方便，将其记为M3_hl_0.6，并规定为原型压气机。在计算中，为了单独研究静子根部间隙的影响，依次改变静子根部间隙为叶片弦长的0%、0.25%、0.5%、1%、1.5%和2%。为了进一步研究静子负荷以及轮毂比变化所带来的影响，本文又另外计算了两组不同压气机形式的结果。一方面，在原型压气机基础上增大静子出口气流角，使得静子在设计点时工作在常规负荷，对应叶中截面D因子为0.45，将其记为M3_sl_0.6；另一方面，在保证静子负荷与原型压气机基本不变的条件下，将其轮毂比增大为0.75，并记为M3_hl_0.75。表1给出了这三个不同形式的压气机静子的详细参数。转子在设计点主流区的D因子在0.50左右，其叶尖间隙始终为弦长的1%。

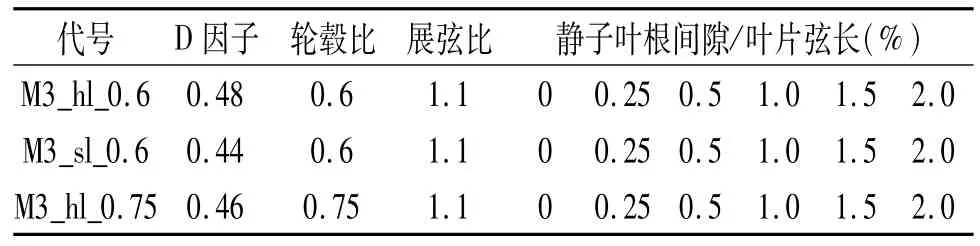
表1 静子参数及间隙值

1.3 三种不同形式压气机特性对比

图2给出了所计算的三个不同形式的压气机的静子压升特性以及展向参数对比，其中压升采用尖部的壁面静压进行计算，流量系数用叶中切线速度无量纲。这三个压气机在流量状态比较小时，静子根部都会出现角区失速，使得特性出现突变。对于小轮毂比条件下的两个压气机，其特性以及展向参数的变化规律基本相同，只是负荷有所不同。对于中等轮毂比形式的压气机，其特性上表现出的明显特征是流量裕度增大，静子静压升偏低，而D因子介于高负荷与常规负荷之间。

图2 压气机特性以及展向参数对比

另外，为了便于后面分析，在特性线上用红圈标示出一些典型的状态点，分别为设计点、静子根部刚进入角区失速点以及近失速点，对于小轮毂形式的两压气机，标示点记为：DE1、CS1、NS1，流量系数对应为：0.6、0.53、0.50；对于中等轮毂比形式的压气机，标示点记为：DE2、CS2、NS2，流量系数对应为：0.55、0.50、0.43。

2 计算结果分析

2.1 小轮毂比高负荷压气机悬臂静子间隙影响

为了研究悬臂静子间隙的影响，以M3_hl_0.6这套压气机叶片为例，来分析静子根部间隙的变化对静子特性和静子通道流动的影响。

2.1.1 间隙对静子特性的影响

图3（a）和图4（a）分别给出了小轮毂比高负荷压气机M3_hl_0.6在不同静子根部间隙时，静子的静压升特性和总压损失特性，其中τ表示间隙大小。对于静子没有间隙的情况，当流量系数减小到0.53（CS1）附近时，静子的静压升系数出现突降，损失突增，从后面的分析中可以看到，这与静子叶根突然分离增大并发展为角区失速相关。为了方便讨论，统一称流量系数大于CS1点时为大流量系数，此时静子根部的角区分离为弱分离形式；而流量系数小于CS1点（包括CS1）时为小流量系数，此时静子根部出现角区失速；在后面对于常规负荷和中等轮毂比压气机的分析中，也采用类似定义。

从图中可以看出，在静子根部引入间隙后，静子的特性出现了明显的变化。在根部角区失速发生前的大流量状态，间隙的引入使得静子的静压升降低，损失增大；当静子根部间隙为0.25%弦长时，静子特性恶化最明显，随着间隙的增大，静子特性逐渐改善，当间隙增大到1%弦长时，静子特性基本达到最优，并且随间隙的变化不敏感。在静子根部发生角区失速后的小流量状态，间隙的引入使得静子特性得到明显改善；而静子特性随间隙变化规律与大流量状态时基本类似，同样在间隙达到1%弦长时，特性达到最优。另外，计算结果表明，静子根部间隙的引入与变化，对压气机的流量裕度都没有明显影响。因此，对于M3_hl_0.6这套压气机叶片而言，悬臂静子的最佳间隙为1%弦长左右。

图3 悬臂静子在不同间隙时的静压升特性

图4 悬臂静子在不同间隙时的总压损失特性

2.1.2 间隙对角区分离的影响

为了分析悬臂静子间隙对静子特性影响的物理机制，下面以M3_hl_0.6这套叶片为例，分析静子根部间隙变化对静子通道内流动的影响。前面的研究表明，在角区失速发生前后的大流量状态和小流量状态，静子根部间隙的影响表现出不同的规律，因此，这里选取了设计点和近失速点两个状态进行分析。图5和图6分别给出了设计点和近失速点时，吸力面、轮毂的壁面极限流线随间隙的变化过程，机匣上的壁面流线没有明显的分离结构，在此没有给出。图7给出了不同间隙时，静子总压损失的展向分布。

图5 不同间隙静子吸力面和轮毂的壁面流线-设计点

图6 不同间隙静子吸力面和轮毂的壁面流线-近失速点-设计点

图7 间隙变化对悬臂静子总压损失展向分布的影响

对于设计点而言，当根部没有间隙时，根尖仅有很弱的角区分离，分离仅局限于叶片表面。当静子根部引入很小的间隙时（0.25%弦长），泄漏流并没有减弱根部的角区分离，反而使得静子根部的角区分离显著增强。一方面，静子根部的角区分离的展向尺度明显增大，另一方面，从轮毂的极限流线可见，在泄漏流与端壁二次流相遇形成的分离线附近，靠近端壁的流体在通道中后部发生倒流。从图7的损失分布可见，0.25%间隙时，叶根40%叶高以内的区域内的损失明显增大。当静子叶根间隙增大到0.5%弦长时，静子根部的角区分离显著减小，靠近轮毂的倒流明显减弱，仅在叶片通道出口处存在小的回流区。相应的，静子根部的高总压损失的展向范围减小到20%叶高以内，这主要是泄漏流和端壁附面层导致的。当间隙增大到1%叶高时，静子根部的分离彻底消失，根部的高损失区进一步减小，受泄漏流增强的影响，总压损失的幅值有所增大。间隙继续增大，静子根部的流动主要表现为泄漏流增强导致的根部流动的缓慢恶化。静子根部间隙的变化对尖部流动的影响非常小。

通过检查角区失速发生前的各个流量状态的流场，静子间隙的影响规律基本与设计点相同。但是，在静子根部发生角区失速前，静子根部的角区分离表现得比设计点更难吹除，在间隙为0.5%弦长时，轮毂的极限流线上仍可以看到明显的倒流，叶根的高损失区的展向尺度也明显大于1.0%间隙的情况，受限于篇幅，这里没有给出具体的流场结果。

在近失速点时，静子根部的流动受间隙的影响规律与设计点时大体上一致，同样是在间隙达到1%弦长时，静子根部的角区分离被彻底吹除。但是，在静子根部间隙很小时（0.25%弦长），表现出与设计点截然相反的规律，间隙的引入使得静子根部的角区分离有所减弱。从轮毂的极限流线可见，在静子根部无间隙时，在通道中部靠近吸力面的位置存在大的回流区，当根部存在间隙后，这一回流区消失了，分离主要表现为靠近分离线的倒流。结合静子的总压损失分布可见，间隙的引入均使得静子根部的总压损失减小，减小程度随着间隙的增大而增强，在间隙达到1%弦长时，根部的损失达到最小。另外，尖部的角区分离有随着间隙的增大而增强的趋势，这与根部流动改善后，尖部的流量系数减小相关。

2.2 静子负荷水平的影响

为了研究负荷水平变化后悬臂静子间隙的影响，计算了小轮毂比常规负荷压气机（M3_sl_0.6）的情况，并与小轮毂比高负荷压气机（M3_hl_0.6）的情况进行对比。图3（b）和图4（b）给出了M3_sl_0.6在不同间隙时的静子特性，通过对比发现，静子特性随间隙变化表现出来的规律与高负荷时相同，通过对比分析流场参数以及角区分离随间隙的变化规律也得到同样的结果。

2.3 轮毂比的影响

为了分析轮毂比变化后悬臂静子间隙的影响，计算了中等轮毂比高负荷压气机（M3_hl_0.75）的情况，并与小轮毂比高负荷压气机（M3_hl_0.6）的情况进行对比。图3（c）和图4（c）给出了M3_sl_0.6在不同间隙时的静子特性，通过对比发现：静子特性随间隙变化的规律大体上基本不变，但还是存在一些明显的差别：首先，最佳间隙值减小为弦长的0.5%；其次，对于静子根部间隙不小于0.5%弦长的情况，当流量系数减小到近失速点附近时，静子特性突然恶化；最后，计算结果表明，间隙的引入使得压气机的流量裕度略有减小。

从特性的对比分析可知，轮毂比增大后，间隙变化的影响规律主要在小流量状态时发生变化，这里以静子根部刚发生角区失速后的流量状态（CS）和近失速状态（NS）进行分析，图8和图9分别给出了对应的静子通道壁面极限流线。

可见，当轮毂比增大后，静子根尖流动的相互影响增强。在CS状态，随着间隙的增大，静子根部的角区分离减弱，而尖部的角区分离的展向尺度显著增大，这使得悬臂静子在更小的间隙（0.5%弦长）时特性达到最优。在近失速状态，静子根部间隙变化对尖部流动的影响更强，当静子间隙增大到0.5%弦长或者更大时，尖部发生角区失速，而根部的角区分离彻底消失，这是导致静子特性在近失速点时显著恶化的原因。

图8 不同轮毂比的悬臂静子流动受间隙变化的影响- CS状态

图9 中等轮毂比的悬臂静子流动受间隙变化的影响-近失速点

3 结论

本文利用经过校验的CFX软件计算方案，计算分析了某单级低速压气机在不同流量系数、不同负荷水平和不同轮毂比情况下，静子根部径向间隙变化（0%～2%弦长）对静子流动和特性的影响，得到以下主要结论。

1）与叶栅中情况类似，在压气机中，悬臂静子同样存在一个特性上表现最优的最佳间隙，最佳间隙值较小，本文中为弦长的0.5%～1%。

2）在大流量状态，无间隙的静子叶根未发生角区失速，间隙的引入主要表现为泄漏流引起的掺混损失与堵塞的增大，从而使得特性恶化。

3）在小流量状态，无间隙的静子叶根发生角区失速，间隙的引入能有效地抑制角区失速，从而改善根部的流动状况，使特性变优。

4）在间隙很小时，泄漏流很弱，泄漏流并不一定能够减弱角区分离；本文中，当静子根部未发生角区失速时，静子根部引入0.25%弦长的间隙，使得根部的角区分离明显增强；但是，在静子根部发生角区失速后，间隙的引入消除了通道中部靠近吸力面的回流区，进而使得分离减弱。

5）压气机设计状态负荷水平减小后，间隙的影响规律基本不变。

6）轮毂比增大后，最佳间隙值有减小的趋势，这与轮毂比增大后，根尖流动的相互作用增强有关；此外，尖部的角区分离对静子根部间隙或角区分离程度的变化更加敏感，在近失速点时，随着静子根部角区失速的吹除，尖部发生角区失速。