基于Fuzzy分析的假眼小绿叶蝉与天敌蜘蛛的数量关系
张书平,钱广晶,毕守东,周夏芝,李 尚,王振兴,邹运鼎,王建盼
(1.安徽农业大学理学院,合肥 230036;2.安徽农业大学林学与园林学院,合肥 230036)
害虫与天敌之间是相互依存和相互制约的关系,这种关系是在长期的进化过程中形成的,它包括时、空、量、构、序等方面的内容,其中数量关系是重要的内容之一[1-2]。在昆虫种群数学生态学的研究中,对害虫及其天敌的数据是通过抽样得来的,对于大量的数据首先要进行分级统计,通常采用以其精度为级宽的连续等分分明分级。由于采用不同精度的级宽,会得出不同的结果,使结果带有很大的主观性和偶然性,便不能准确地反映害虫及天敌等研究对象的客观状态及集中性,通过时间范畴和空间范畴抽样得来的数据更会产生一些误差。数理统计的一个重要特点是采用抽样估计的方法,以样本值估计群体特征。过去研究茶园害虫与其天敌之间的数量关系多是直接用调查得来的数据进行相关分析或关联度分析[3-13],如柯胜兵等研究大别山区不同海拔茶园茶尺蠖Ectropis oblique hypulina、茶叶斑蛾 Eterusia aedea、茶卷叶蛾 Homona coffearia、茶黄蓟马Scirtothrips dorsalis、茶丽纹象甲Myllocerinus aurolineatus、茶角胸叶甲 Basilepta melanopus 与捕食性天敌的关系时,把间隔15~20 d 调查一次的数据不经修匀直接进行灰色关联度分析。但是,因存在上述缺陷,影响其结果的准确性。Fuzzy 分级统计的结果能较好地反映害虫及其天敌种群动态的客观情况,减少了主观性和偶然性[14-15]。徐飞、公茂莲和王万雄等[16-18]用非对称指数型模糊数、模糊相似优先比和模糊集理论用作预报或研究小绿叶蝉与其天敌的关系,取得较好的效果。党凤花等[3]研究龙井43 茶园蜘蛛在茶园节肢动物中占捕食性天敌的77.03%。刘飞飞等[11]研究黄山大叶种茶园蜘蛛占捕食性天敌总量的77.36%~84.78%。柯胜兵等[5-8]研究大别山区低海拔茶园蜘蛛占捕食性天敌总量的87.45%,表明蜘蛛是茶园主要捕食性天敌。为了明确假眼小绿叶蝉与其天敌蜘蛛的数量关系,本研究采用Fuzzy 分级法和灰色关联度法相结合,研究对假眼小绿叶蝉在数量上跟随关系密切的蜘蛛种类,以期为利用天敌蜘蛛防治假眼小绿叶蝉提供科学依据。
1 材料和方法
1.1 调查地点和时间
调查地点为安徽农业大学科技示范园茶园,调查茶树品种为树龄13年的乌牛早和白毫早,茶园面积均为0.2 hm2。调查时间为2015年3月28日—11月14日。2016年3月27日—11月17日,约 15 d调查一次,2015年调查 17 次,2016年调查 16 次。茶园周边为其他品种茶园,茶园按常规措施管理,但不施用农药。
1.2 调查方法
采用平行跳跃法随机在茶园选取3 行,茶树行宽为2 m,每行间隔1 m 取2 m 长的样方。每行10个样方,3 行共30 个样方。先目测调查,每样方随机选取10 片叶,调查一些不易振落害虫及天敌种类和个体数,然后用沾有0.1%洗衣粉水溶液的搪瓷盘对样方中的所有枝条进行盘拍(本文所用洗衣粉品牌为雕牌洗衣粉,厂家为上海隆鑫贸易有限公司,搪瓷盘口长为40 cm,宽30 cm),调查记载害虫及其天敌蜘蛛个体数,对于一部分不能准确鉴定的物种样本编号保存,装瓶带回室内根据书籍《中国茶树害虫及其无公害治理》鉴定或请专家鉴定。
1.3 数学分析方法
1.3.1 模糊分级法
在论域[A1,A2,A3,…,An,…,Am]上按问题的性质和要求规定的一个隶属函数μi,叫作Fuzzy分级隶属函数。把通常连续等分分明分级的频数做原始数据,设原始数据为[a1,a2,a3,…,an,…,am-1,am],称为第i个Fuzzy等级的Fuzzy频数。它在论域上的分布曲线叫Fuzzy频数曲线[19-20]。用变异系数CV比较Fuzzy频数和等分分明分级频数的变异大小为标准差为均数。
1.3.2 假眼小绿叶蝉与7种天敌Fuzzy频数间的灰色关联度分析
用灰色关联度方法[21],将假眼小绿叶蝉与7种天敌蜘蛛Fuzzy频数分别看作一个本征系统,假眼小绿叶蝉Fuzzy频数Y作为该系统的参照序列,将7种天敌Fuzzy频数Xi作为该系统的比较序列,不同等级的假眼小绿叶蝉Fuzzy频数和7种天敌Fuzzy频数在k点上的效果白化值进行双序列关系分析。经数据均值化后,利用关联度公式R(Yi,Xj)=求出7种天敌Fuzzy频数(Xj)与假眼小绿叶蝉Fuzzy频数Y数量间的关联度,rij为关联系数,其公式为:

式中ρ为分辨系数,取值介于0~1之间,一般取ρ=0.5,为扩大各关联度之间的差异,本文取ρ=0.8;Δ=为序列Yi与Xj在第k点上的绝对值差为1级最小差,min min为2级最小差,同理,max分别为1级和2级最大差。
关联度值越大,表明天敌与假眼小绿叶蝉的跟随关系越密切。
2 结果与分析
2.1 乌牛早茶园天敌与假眼小绿叶蝉数量的分级
现分别将乌牛早茶园2015年3月28日—11月14日和2016年3月27日—11月19日假眼小绿叶蝉和7种蜘蛛类天敌自然种群系统调查的原始数据列于表1、表2。表中数据是空间上抽样得来的,也是约半个月调查一次得来的,这是从时间上抽样而不是每天调查一次的连续调查结果。

表1 2015年乌牛早茶园假眼小绿叶蝉及其7 种蜘蛛天敌种群动态Table 1 Population dynamics of Empoasca vitis and their 7 species of spider natural enemies in the‘Wu Niu zao’tea garden in 2015 ind·30 plots-1
为了了解茶园假眼小绿叶蝉和7 种蜘蛛天敌2015年从 3月 28日—11月 14日和 2016年从 3月 27日—11月 19日自然种群动态,将表1、表2中数据按照(50 只/30 样方)的级宽进行等分分明分级统计(分级标准主要根据假眼小绿叶蝉种群数量变化幅度,级宽不能太宽也不能太窄,因而选择50只/30 样方),算出各级出现的频数(即作为Fuzzy 分级统计的原始数据),结果绘于图1和图2。再以50(只/30 样方)为级宽的频数作为原始数据(即[a1,a2,a3,…,an,…,am-1,am]),进行 Fuzzy 分级统计,现规定Fuzzy 分级隶属函数为:

可看出图1、图2中b 图的数据集中性明显高于 a 图。
2.2 白毫早茶园天敌与假眼小绿叶蝉数量的分级
现分别将白毫早茶园2015年3月28日—11月 14日和 2016年 3月 27日—11月 19日假眼小绿叶蝉和7 种蜘蛛类天敌自然种群系统调查的原始数据列于表3、表4。表中数据既是空间上抽样得来的,也是约半个月调查一次得来的,这既是从空间上也是从时间上进行抽样。
为了了解茶园假眼小绿叶蝉和7 种蜘蛛天敌2015年从3月28日—11月14日和2016年从3月 27日—11月 19日自然种群动态,将表3、表4中数据按照50 只/30 样方的级宽进行等分分明分级统计,算出各级出现的频数,结果绘于图3和图4。再以50(只/30 样方)为级宽的频数作为原始数据(即[a1,a2,a3,…,an,…,am-1,am]),进行Fuzzy 分级统计(运算公式如上),对计算所得的以50(只/30 样方)为级宽的分明分级频数作原始数据进行计算Fuzzy 频数,将结果也分别绘于图3和图4中。

图1 乌牛早茶园2015年假眼小绿叶蝉与7 种蜘蛛的分明分级频数曲线(a)和Fuzzy 频数曲线(b)Figure 1 Distinct grading Frequency Curves (a)and Fuzzy Frequency Curves (b)of 7 species of spider and Empoasca vitis in Wuniuzao tea garden in 2015
由图3和图4可看出b 图中数据集中性高于a 图。
为了比较Fuzzy 分级频数及等分分明分级频数的差异,特将两种频数进行t 检验,结果列于表5。
由图1、图2、图3、图4可看出 Fuzzy 分级频数集中性大于等分分明分级频数,由表5可看出Fuzzy 分级频数与等分分明分级频数之间假眼小绿叶蝉、鳞纹肖蛸、锥腹肖蛸差异显著,除此之外,白毫早茶园的八斑球腹蛛两种频数间差异基本显著。由表1、表2、表3、表4进一步分析可看出,假眼小绿叶蝉、鳞纹肖蛸、锥腹肖蛸的数量显著高于其他5 种蜘蛛的数量,即表明种群数量越大,两频数间差异越大,说明在种群数量大时,用等分分明分级与实际情况误差大。通过计算比较得出所有分明分级频数的变异系数都大于Fuzzy 频数,即相比较来说Fuzzy 分级比等分分明分级变异小,准确性要高。
2.3 两年两种茶园与假眼小绿叶蝉数量关系密切的天敌种类
用灰色关联度法求得两年两品种茶园假眼小绿叶蝉与7 种蜘蛛Fuzzy 频数的关联度值,并将其列于表6。与假眼小绿叶蝉数量上关系密切的前3位天敌,乌牛早茶园2015年是鳞纹肖蛸0.853 4、锥腹肖蛸0.822 2 和八斑球腹蛛0.799 3,2016年是锥腹肖蛸0.768 1、鳞纹肖蛸0.761 0 和粽管巢蛛0.744 9。白毫早茶园2015年是纹肖蛸0.862 0、锥腹肖蛸0.830 5 和八斑球腹蛛0.797 3,2016年是八斑球腹蛛0.904 5、锥腹肖蛸0.864 3 和鳞纹肖蛸0.843 9。两种茶园两年与假眼小绿叶蝉数量关系密切的前3位天敌中都有鳞纹肖蛸和锥腹肖蛸,八斑球腹蛛4次中出现3 次。

图2 乌牛早茶园2016年假眼小绿叶蝉与7 种蜘蛛的分明分级频数曲线(a)和Fuzzy 频数曲线(b)Figure 2 Distinct grading Frequency Curves (a)and Fuzzy Frequency Curves (b)of 7 species of spider and Empoasca vitis in Wuniuzao tea garden in 2016

表3 2015年白毫早茶园假眼小绿叶蝉及其7 种蜘蛛天敌种群动态Table 3 Population dynamics of Empoasca vitis and their 7 species of spider natural enemies in the‘Bai hao zao’tea garden in 2015 ind·30 plots-1

(续表3)
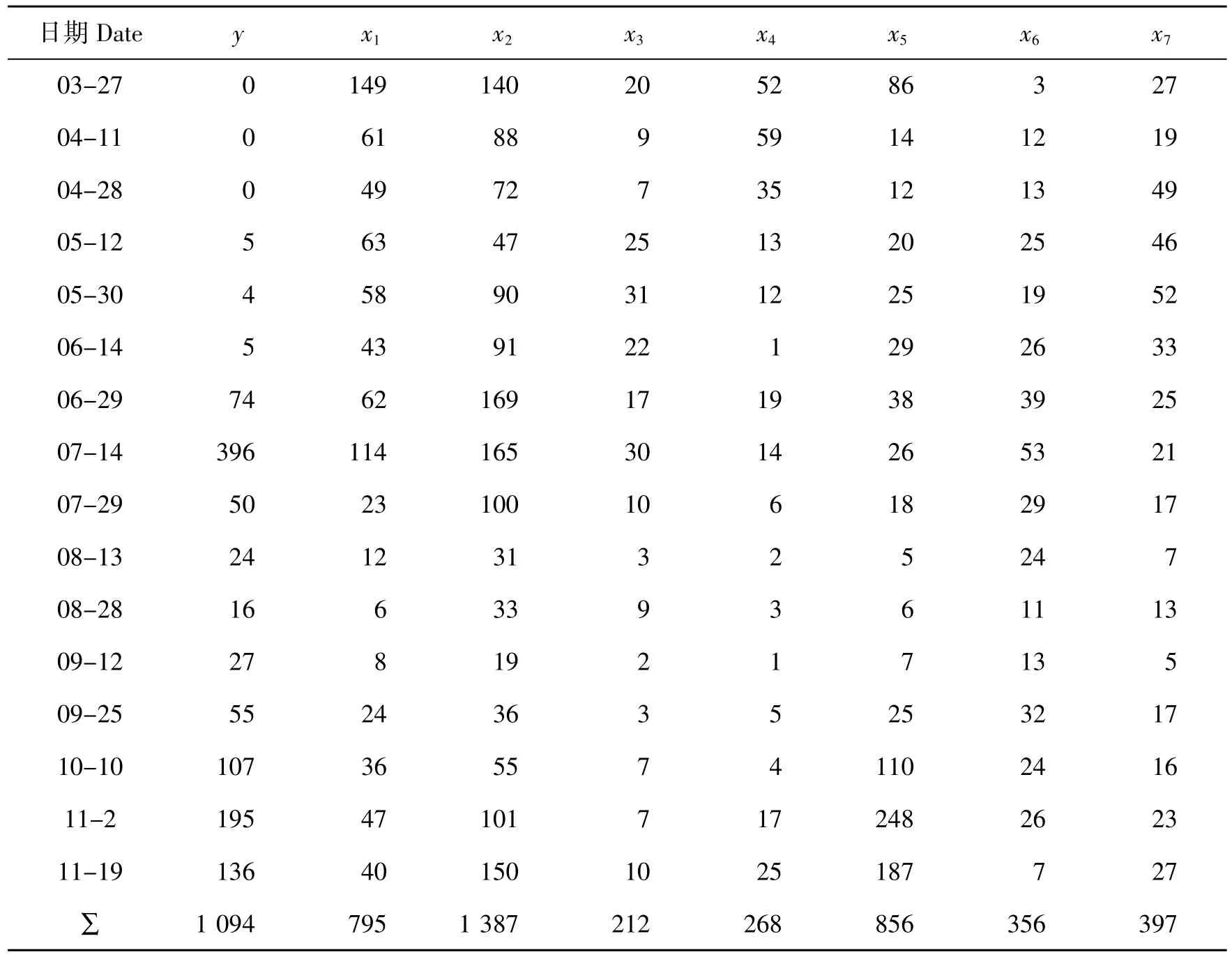
表4 2016年白毫早茶园假眼小绿叶蝉及其7 种蜘蛛天敌种群动态Table 4 Population dynamics of Empoasca vitis and their 7 species of spider natural enemies in the‘Bai hao zao’tea garden in 2016 ind·30 plots-1
3 讨论与结论
运用Fuzzy 分级法和灰色关联度法研究7 种天敌蜘蛛与假眼小绿叶蝉在数量关系上的密切程度,与直接用调查数据进行分析的结果进行比较,余燕等[22]直接用调查数据未经修匀处理研究害虫与天敌在数量关系上的密切指数。与Fuzzy 分级后的分析结果相比,乌牛早茶园2015年和2016年前4 位天敌都只有锥腹肖蛸和粽管巢蛛相同,白毫早茶园与假眼小绿叶蝉数量上关系密切的前4 位天敌,与Fuzzy 分级后的结果相比,2015年前4 位天敌只有粽管巢蛛和锥腹肖蛸相同,2016年只有八斑球腹蛛、锥腹肖蛸和鳞纹肖蛸相同,表明两种方法分析的结果还是有差异的。华尧楠等[23]提出Fuzzy 分析在病虫测报会商会中的应用,结果证明预报结果与实况吻合度高。赖学连、靳桂芝等[24-25]用Fuzzy 分级法研究二代棉铃虫发生量和一代三化螟蛾发生量,预报结果与实况的历史符合率达到91.67%和95%,总体来说Fuzzy 分级后的结果进行分析更科学一些。
Fuzzy 分级统计相比于相关分析、回归分析等,在样本数量多、样本数值大的抽样数据中更能显示出其优点。Fuzzy 分级统计与常用的分明分级统计比较,其特点是,每个原始数据与几个等级发生联系,分明分级每个原始数据只与一个等级发生联系,Fuzzy 频数与原始数据和Fuzzy 隶属函数有关,无明显的分级界限,Fuzzy 频数的直接图示是曲线,可保持原始数据的精度,因此用此法分级的数据进行灰色关联度分析,其结果更接近实际。

图3 白毫早茶园2015年假眼小绿叶蝉与7 种蜘蛛的分明分级频数曲线(a)和Fuzzy 频数曲线(b)Figure 3 Distinct grading Frequency Curves (a)and Fuzzy Frequency Curves (b)of 7 species of spider and Empoasca vitis in Baihaozao tea garden in 2015

图4 白毫早茶园2016年假眼小绿叶蝉与7 种蜘蛛的分明分级频数曲线(a)和Fuzzy 频数曲线(b)Figure 4 Distinct grading Frequency Curves (a)and Fuzzy Frequency Curves (b)of 7 species of spider and Empoasca vitis in Baihaozao tea garden in 2016

表6 假眼小绿叶蝉与7 种蜘蛛Fuzzy 频数的关联度Table 6 Correlation between Fuzzy frequencies of 7 species of spider and Empoasca vitis

