基于自触发的异构多智能体协同输出调节

刘娟 张皓 王祝萍

近年来多智能体系统的分布式协同输出调节在多机器人和无人车等方面的应用中发挥着越来越重要的作用[1−3],典型的协同输出调节问题包括一致性以及编队等问题的研究[4−10],早期的输出调节的研究对象主要是单个智能体,而协同输出调节针对的是多智能体系统,控制目标是使所有的多智能体能够渐近跟踪外部参考输入信号和对外部干扰进行抑制.在协同输出调节问题中,并非所有的智能体都能够接收到外部系统的信号,因此不能采用集中式和分散式控制解决问题.浙江大学的Xiang 等[11]首先提出了一种基于附加可检测条件的前馈控制用于控制同构线性多智能体系统.哈尔滨工业大学的Wang 等[12]研究了固定拓扑下多智能体系统的分布式协同鲁棒输出调节问题,并假设通信拓扑包含一个以节点0 为根的有向生成树且没有环路.然而无环假设是一个较强的假设,在此假设下,这种控制策略不能应用到通信拓扑为无向图的多智能体系统中,为了去掉此假设,香港中文大学的Su 等在文献[13]中研究了线性多智能体系统的协同输出调节问题,提出了一种基于分布式观测器的方法,在该控制器的作用下,外部系统的信息能够传递给多智能体子系统,然而控制器的设计需要用到全局通信拓扑的拉氏矩阵的最小非零特征值.于是,为了解决这一问题,Li 等在文献[14]中针对有向通信拓扑设计了分布式自适应输出调节控制机制.

在多智能体系统的实际应用中,每个智能体进行通信以及信息的获取等活动时所需的能量都是从自身的微型传感设备所获取的,但是每个智能体所能获取的能量是有限的,所以减少智能体的通信能量损耗具有非常重要的意义.然而现有的许多控制器的设计中都需要智能体之间进行连续通信,控制器也需要持续地更新,因此,为了减少智能体自身控制执行器的更新次数以及智能体之间的通信次数,提出了事件触发控制策略.在事件触发传输机制中,只有当系统的实际状态和参考值之间的差距大于一定的阈值时,即系统发生较大变化时,才对当前时刻状态进行更新,因此能够有效降低计算机资源消耗.在基于系统状态已知的情况下,Guo 等在文献[15]中提出了一种基于状态采样的事件触发控制机制,通过使用这种方法,能够将多智能体的一致性问题转化成一个时滞系统的稳定性问题.华中科技大学的Yin 等[16]提出了一种分布式事件触发控制机制用于解决异构多智能体的一致性问题.然而在实际应用中,系统状态往往很难测量,于是,同济大学的Zhang 等[17]提出了一种基于状态观测器的输出反馈事件触发控制机制,对状态不能直接测量的系统实现了状态反馈控制作用.

在现有相关文献研究的基础上,Yang 等[18]设计了基于事件触发的多智能体系统的协同输出调节问题,在事件触发条件上增加了自适应参数,且智能体不需要连续知道相邻节点的状态信息.但在事件触发策略应用中,需要时刻监测触发条件是否满足.基于这种情况,Hu 等[19]研究了基于分布式观测器的事件触发协同输出调节问题,提出了一种自触发控制策略.在自触发控制下,智能体可以根据自身信息以及邻居节点的信息计算下一触发时刻,从而避免了对事件触发条件的连续监测.

基于上述的研究,本文以线性异构多智能体系统为研究对象,设计了一种自触发规则分别用于状态反馈和输出反馈两种不同情况下的分布式自适应控制器中,降低了多智能体系统中对对象监测的硬件要求,为了使控制器在更新时只需知道局部信息就能达到控制目标,引入了自适应控制策略,从而可以避免使用多智能体系统的全局信息,同时智能体不需要连续知道邻居节点的状态.

符号说明:AT表示A的转置;Rn×n表示n×n维的实矩阵;A⊗B表示矩阵A和B的Kronecker积;表示A的范数;diag{A1,···,AN}表示对角线上的项为Ai的分块对角矩阵,i=1,···,N.

1 图论知识及问题描述

1.1 图论知识

多智能体系统通信拓扑可用G=(V,E,A)表示,其中,V={1,2,···,N}代表节点数集,E ∈V×V表示边,A表示邻接矩阵,若节点i ∈V和节点j ∈V相邻,则用(i,j)表示节点i到节点j的边.在无向图中,(i,j)与(j,i)是等价的,如果图中至少有一个节点能够通向其他任意一个节点,则称该图中存在有向生成树.邻接矩阵A=[aij]∈Rn×n,aij=1 表示i和j互为邻居节点,可以进行通信;反之,则aij=0.拉氏矩阵L=[lij]∈Rn×n,其中表示节点i的邻居集.

多智能体系统中包含外部系统时,通信拓扑如图1 所示可描述为,其中节点0 代表外部系统,其他节点为1,···,N.其中节点0 所代表的外部系统到跟随的多智能体子系统节点1,···,N是有向的,而子系统节点1,···,N之间信息传递是无向的.对于节点i ∈V.如果节点i能够得到外部系统的信息,则用ai0=1 表示;否则ai0=0.

图1 多智能体系统的通信拓扑图Fig.1 Communication diagraph of the multi agent systems

引理1[20].若图包含一个以节点0 为根的有向生成树,则拉氏矩阵只有一个零特征值且所有的非零特征值都含有正实部.可表示为

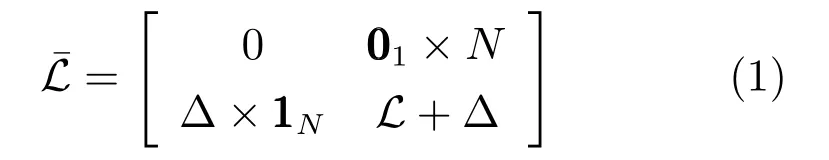
令H=L+∆,且∆=diag{a10,···,aN0}.根据引理1,如果包含一个以节点0 为根的有向生成树,则H是正定的.

1.2 问题描述

考虑N个线性异构多智能体和一个外部系统,其中智能体的动力学方程为

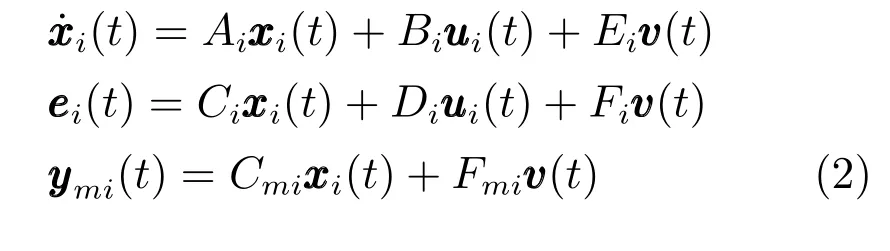
其中,xi(t)∈Rni为智能体i的状态,ui(t)∈Rmi为智能体的控制输入,ei ∈Rq为智能体的被调输出,ymi ∈Ryi为智能体的测量输出.Ai,Bi,Ei,Ci,Di,Fi,Cmi,Fmi为常数矩阵.v(t)∈Rp为被跟踪的外部信号或者需要抑制的扰动信号,动态方程为

其中,S ∈Rp×p为常数矩阵.

在本文中,G为包含i ∈V个节点的无向通讯拓扑图,为了解决线性异构多智能体系统的协同输出调节问题,提出如下假设:

假设1.S矩阵的所有特征值的实部均为非负.

假设2.(Ai,Bi),i ∈V是稳定的.

假设3.(Cmi,Ai),i ∈V是可测的.

假设4.如下线性矩阵方程存在唯一解(Xi,Ui)

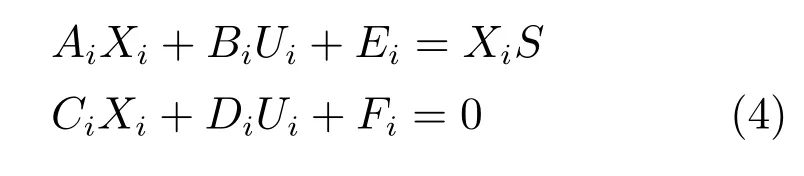
其中,Xi ∈Rni×p,Ui ∈Rmi×p,i=1,···,N.

假设5.包含一个以节点0 为根节点的有向生成树.

以上假设均不失一般性,在现有的相关研究中均存在相同的假设条件.

定义1.在通讯拓扑下,对于多智能体系统(2)和(3)设计的控制器,满足:

1)当v(t)=0,这个闭环系统渐近稳定.

2)对于任意初始条件,总有limt→∞ei(t)=0.那么所设计的控制器能够解决多智能体系统(2)和(3)的协同输出调节问题.

系统的分布式控制结构如图2 所示,每个智能体均有独立的控制器和触发规则,通过通信拓扑进行信息交流,其中一部分智能体能够获得外部系统的信息,而另外一部分不能获得外部系统的信息,因此为了解决多智能体系统的协同输出调节问题,设计合理的控制器和触发规则就显得非常重要.

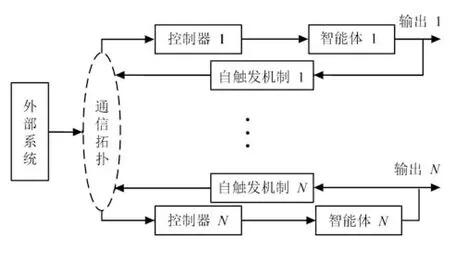
图2 分布式控制系统结构图Fig.2 Structure of distributed control system

2 基于自触发规则的控制器设计

2.1 基于状态反馈的控制器设计

当智能体状态可以测量得到时,设计如下的分布式自适应控制器

注1.Φi(t)中包含的是智能体i的邻居节点和领导者的通信拓扑信息,即公式中的aij和ai0,无向图中,若智能体j是智能体i邻居节点,则aij=1,同样,若与领导者也相邻,则ai0=1;否则,aij和ai0均为0,即代表不能获得除邻居节点之外其他节点的信息,也就是说每个智能体是不需要知道Laplace 矩阵这一全局信息的.

定义智能体i上一触发时刻和当前触发时刻信号的测量误差为

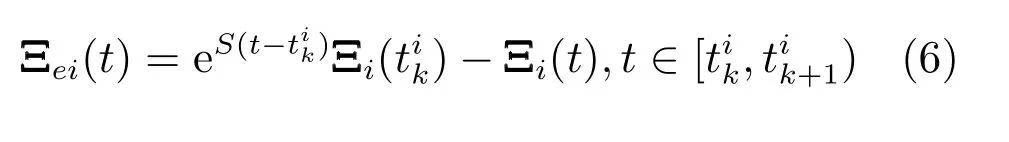
设计触发的关系方程为

其中,βi >0 是一个常数,θi(t)为自触发方程的自适应参数,满足θi(t)>0,因为(t)≥0,所以θi(t)是一个单调不减函数.当事件没有触发之前,ζi(t)≤0.令在时,取则在i触发之前的时间段内,θi(t),Ωi(t)均为常数,然后对进行求导

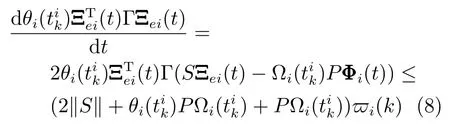
又由于在事件触发时,ζi(t)=0,即

通过式(7)和(8)可以得到一个最小的触发时间关系:

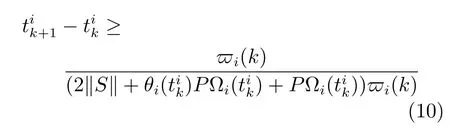
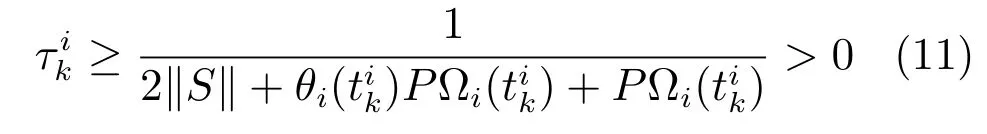
由不等式(11)可知,触发的最小时间大于0,即证得不存在芝诺现象.

注2.芝诺现象指的是事件在有限时间内发生无限次触发,当设计的自触发规则发生芝诺现象,则代表此触发规则是不可行的.

根据上述推导,提出如下自触发算法规则:

步骤1.定义智能体i上一触发时刻的时间为下一触发时刻的起始时刻,定义则通过计算得出触发时刻为:

步骤2.判断智能体i的邻居节点此时有没有触发的,若有触发的,则(k)=(k)−为此时智能体i的邻居节点j的触发时刻,令,返回步骤1重新计算;若此时没有邻居节点触发,则执行步骤3;

步骤3.此时可以得到智能体i下一时刻的触发时间为:

注3.与文献[19]相比,本文的优势在于,一是在设计反馈控制器时,在式(5)中的控制器中增加了自适应参数Ωi(t),二是本文提出的自触发规则中也增加了自适应参数θi(t),这两个自适应参数共同作用可以避免引入通信拓扑拉氏矩阵的最小非零特征值这一全局信息,实现分布式控制.此外,因为已经证明存在一个严格正定的时间间隔,即芝诺现象不存在,所以上述自触发算法不会无限循环.

注4.在此自触发规则作用下,智能体i下一次的触发时刻可以通过自身的信息和邻居节点最近一次触发时刻的信息计算出来,不需要对触发条件进行连续监测,且只有在触发时刻,智能体之间才会进行信息传输,所以自触发能够有效地减少计算机资源损耗和通信代价.

通过将式(5)代入式(2)中,可以得到智能体i的闭环系统为

在此自触发规则下,提出如下基于状态反馈的触发控制策略用来解决基于状态反馈的协同输出调节问题.

定理1.假设1,2,4,5 成立,K1i的取值满足使得Ai+BiK1i是Hurwitz 矩阵,K2i=Ui −K1iXi,P >0 是Riccati 方程PS+STP −δ1PP+δI=0的解,在自触发规则和控制器(5)的共同作用下,若满足:

1)当v(t)=0 时,limt→∞xi(t)=0,limt→∞Ξi(t)=0,i=1,···,N,且当时间t趋于无穷时,自适应参数Ωi(t)和θi(t)趋于某一常数.

2)对于任意初始条件xi(0),Ξi(0)以及v(0),被调输出最终都将趋于0,即limt→∞ei(t)=0,i=1,···,N.

则多智能体系统(2)和(3)能够实现协同输出调节.

证明.首先证明定理1 的第一部分,因为Ai+BiK1i是Hurwitz 矩阵,那么这个闭环系统的稳定性与下面的系统(14)的稳定性是等价的.

为了证明闭环系统的稳定性,选取Lyapunov函数

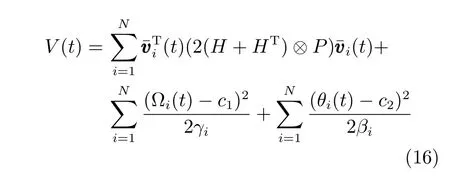
Lyapunov 函数可以分为三部分,即

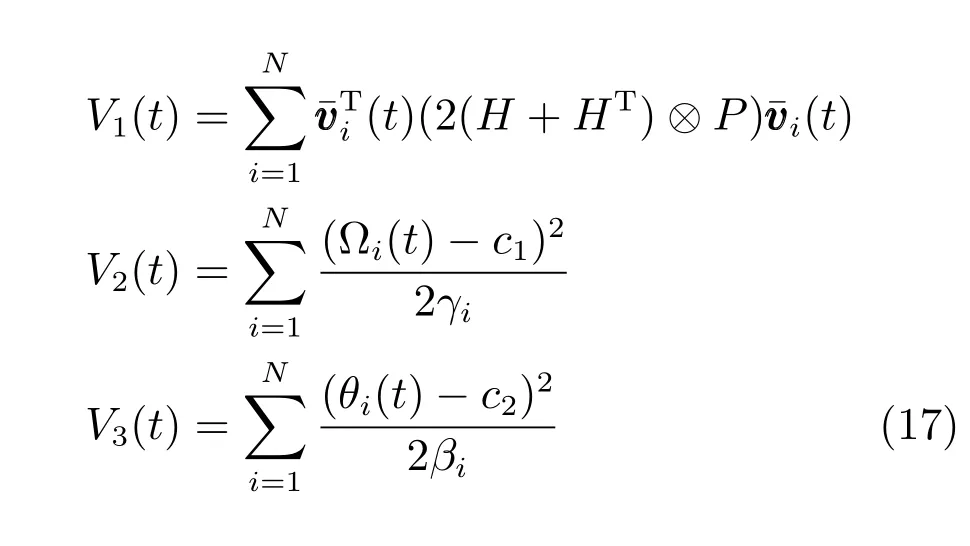
然后分别对其进行求导,c1,c2都是常数.首先对V1(t)进行求导,,得

然后对V2(t)进行求导得

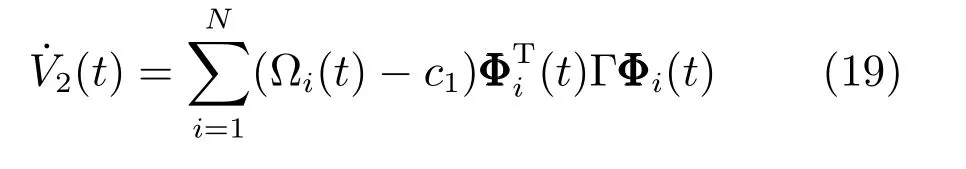
最后,同样可得V3(t)的导数:

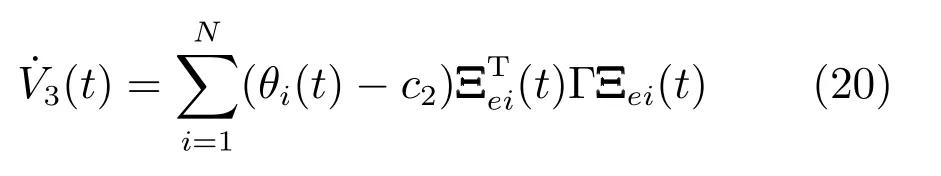
把三部分导数相加得:

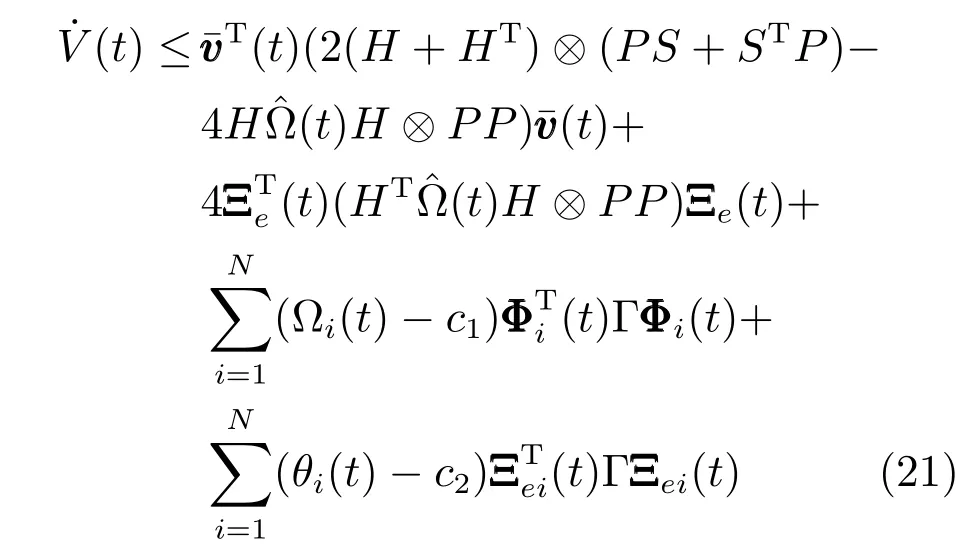
因为Ωi(t)≥1,且是触发时刻所在区间求导,所以根据触发条件ζi(t)≤0,可变换为

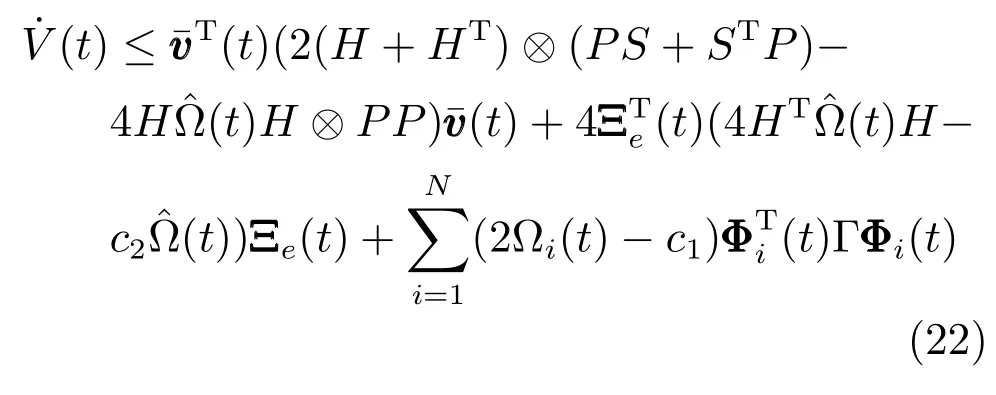
又由于

综上可以得到Lyapunov 函数为

接下来,将证明定理1 的第二部分.由假设4,同时令εi(t)=xi(t)−Xiv(t),可以得到如下表达式

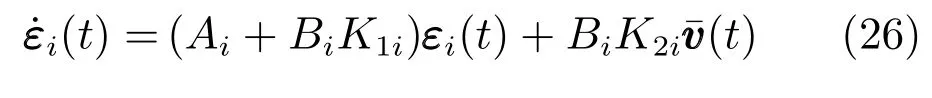
通过已证的定理 1 的第一部分可知limt→∞=0,因此εi(t)的稳定性是与(Ai+BiK1i)εi(t)等价的,由从假设2 可知,Ai+BiK1i是Hurwitz 稳定的,因此可以知道,limt→∞εi(t)=0.

智能体i的被调输出为

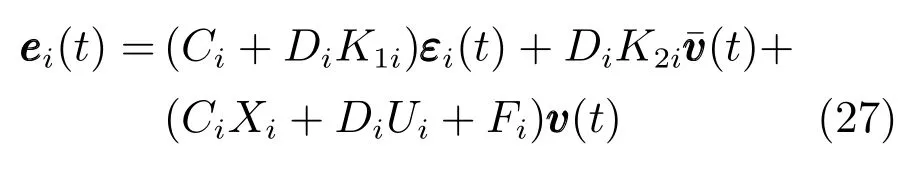
由于 limt→∞=0,limt→∞εi(t)=0,在根据假设4 的第二个方程,所以可以推导出:limt→∞ei(t)=(CiXi+DiUi+Fi)v(t)=0.

2.2 基于输出反馈的控制器设计

在基于状态反馈的控制器设计中,每个智能体本身的状态是可以获得的,但是在实际的应用中,系统状态一般是很难通过测量得到,因此为了解决这个问题,本节设计了基于输出反馈的分布式自适应控制器,如下所示.

其中,Φi(t)的定义与式(5)的定义一样,Υi(t)∈Rni是节点状态的估计值,Qi ∈Rni×pi是常数增益矩阵.把式(28)代入式(2)中,单个节点i的闭环系统如式(29)所示.

令Q=diag{Q1,···,QN},Cm=diag{C1m,···,CmN},Fm=diag{Fm1,···,FmN},则整个系统的闭环形式为

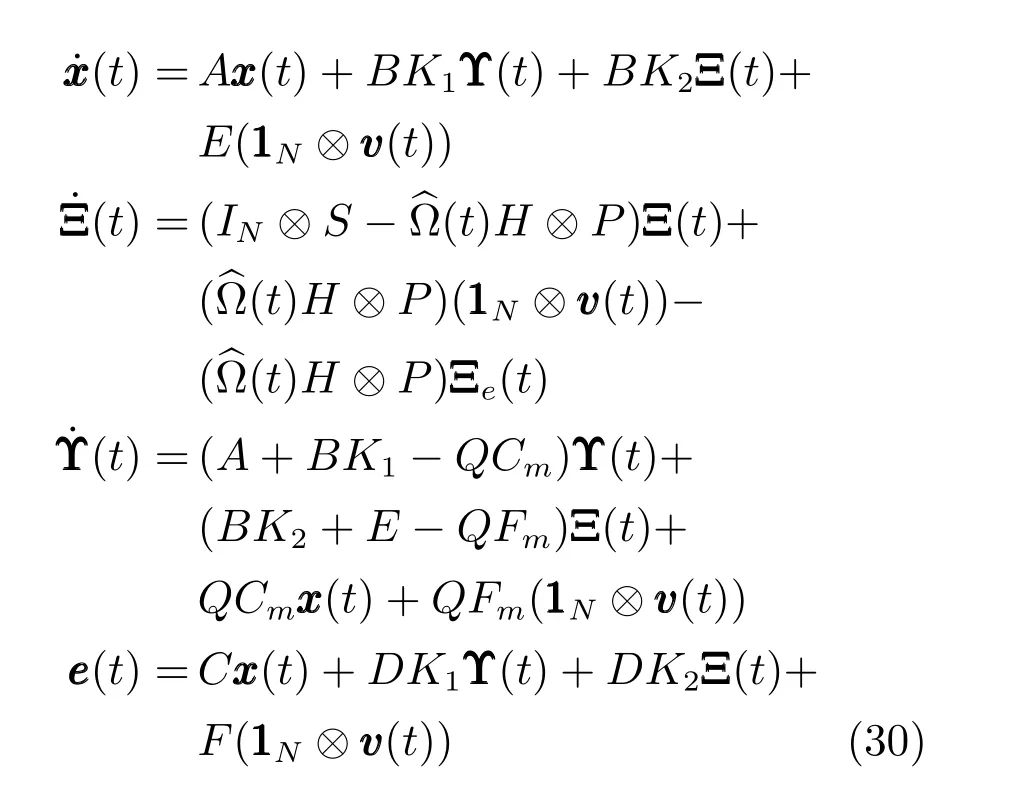
定理2.在假设1∼5 成立的条件下,K1i和Qi增益矩阵的取值分别使Ai+BiK1i和Ai −QiCmi是Hurwitz 矩阵,其中K2i=Ui −K1iXi,在自触发规则和控制器(28)的共同作用下,若满足:

1)当v(t)=0 时,limt→∞xi(t)=0,limt→∞Ξi(t)=0,limt→∞Υi(t)=0,i=1,···,N,且当时间t趋于无穷时,自适应参数Ωi(t)和θi(t)趋于某一常数.

2)对于任意初始条件xi(0),Ξi(0),Υi(0)以及v(0),被调输出最终都将趋于0,即limt→∞ei(t)=0,i=1,···,N.

则在智能体状态未知的情况下,多智能体系统(2)和(3)也能够实现协同输出调节.

证明.令,则式(30)的闭环系统形式可以写成如下形式

智能体i的被调输出为

因为limt→∞ςci(t)=0,limt→∞=0,再根据假设4,可以推出limt→∞ei(t)=0.

3 仿真结果

本节根据提出的定理,采用基于输出反馈的控制器(28)和所提出的自触发规则对4 个跟随机器人(2)和1 个领导机器人(3)组成的多智能体系统进行直角编队仿真实验[21],4 个非完整性移动跟随机器人的动力学模型为

选取Dmi=Di=02×1,Fmi=02×2,i=1,2,3,4.给定参数[a1,b1,c1,d1]=[1,1,1,0],[a2,b2,c2,d2]=[10,2,1,0],[a3,b3,c3,d3]=[2,1,1,10],[a4,b4,c4,d4]=[2,1,1,1].

领导者的动力学模型为

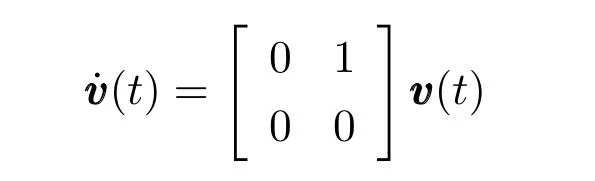
各智能体的初始状态为:v(0)=[0.7984,0.9430]T,x1(0)=[0.6551,0.1626,0.4218]T,x2(0)=[0.4984,0.9597,0.9157]T,x3(0)=[0.5853,0.2238,0.7922]T,x4(0)=[0.2551,0.5060,0.9595]T;观测器Υi(t)的-初始-状态-为:Υ1(0)=[0.7463,0.0103,0.0484]T,Υ2(0)=[0.6679,0.6035,0.5261]T,Υ3(0)=[0.7297,0.7073,0.7814]T,Υ4(0)=[0.2880,0.6925,0.5567]T;估计器Ξi(t)的初值为:Ξ1(0)=[0.2060,0.9479]T,Ξ2(0)=[0.0821,0.1057]T,Ξ3(0)=[0.1420,0.1665]T,Ξ4(0)=[0.6210,0.5737]T.

编队仿真结果如图3 所示,4 个跟随者与领导者能够完成直角编队任务,从图4 和5 可知,多智能体系统调节输出ei(t)能够渐近趋于零.图6 和7分别表示控制器和自触发条件的自适应参数的变化,从图中可以看出这两个自适应参数均渐近趋于有限稳态值.本文中,总的仿真时间50 秒,总平均触发次数为321,平均触发时间间隔为0.1557 秒,相比文献[19]的仿真结果,其平均触发次数均在600 以上,本文中的自触发规则能够有效地减少触发次数,表明本文中的自触发机制不仅能够避免对触发条件进行连续监测,也能够有效降低智能体之间的通信次数.

4 结论

本文设计了基于自触发规则的分布式自适应控制器,在该控制器作用下,异构多智能体系统能够很好地跟踪外部系统.同时,该控制器不需要智能体之间进行连续通信,能够有效降低智能体之间的通信负载,且不需要对触发条件进行连续监测,触发时间可通过自身信息和邻居节点的信息计算获得,降低了硬件设计要求.

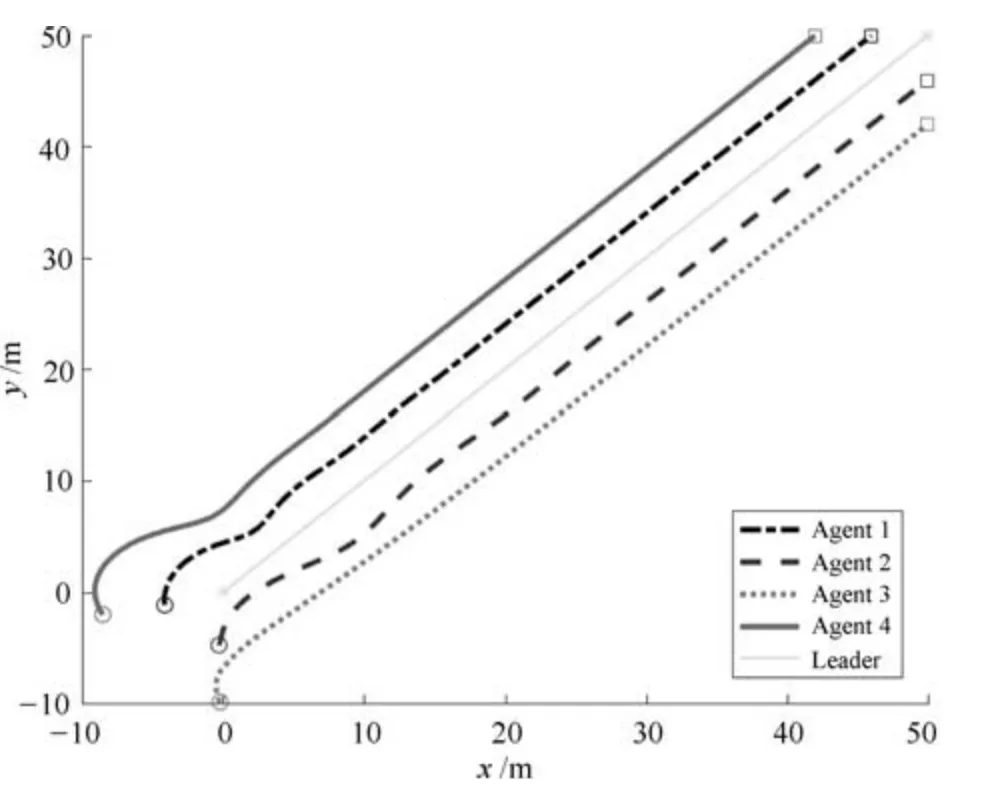
图3 领导者和4 个跟随者的运动轨迹Fig.3 The trajectories of the leader and four followers

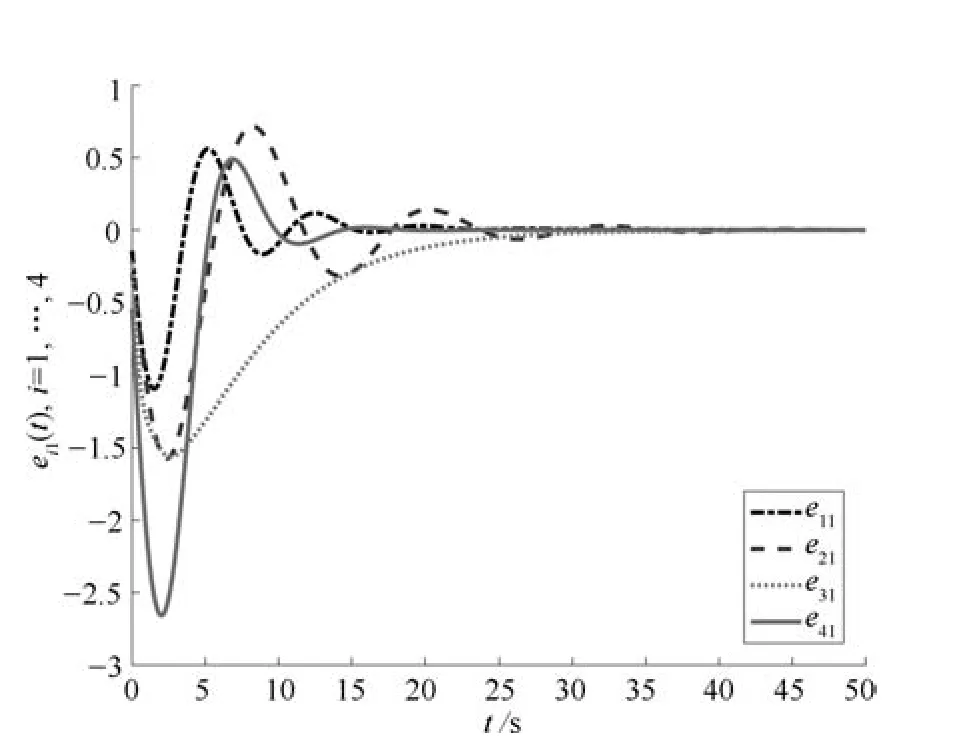
图4 智能体的调节输出ei1(t), i=1,2,3,4Fig.4 Regulated outputs ei1(t), i=1,2,3,4

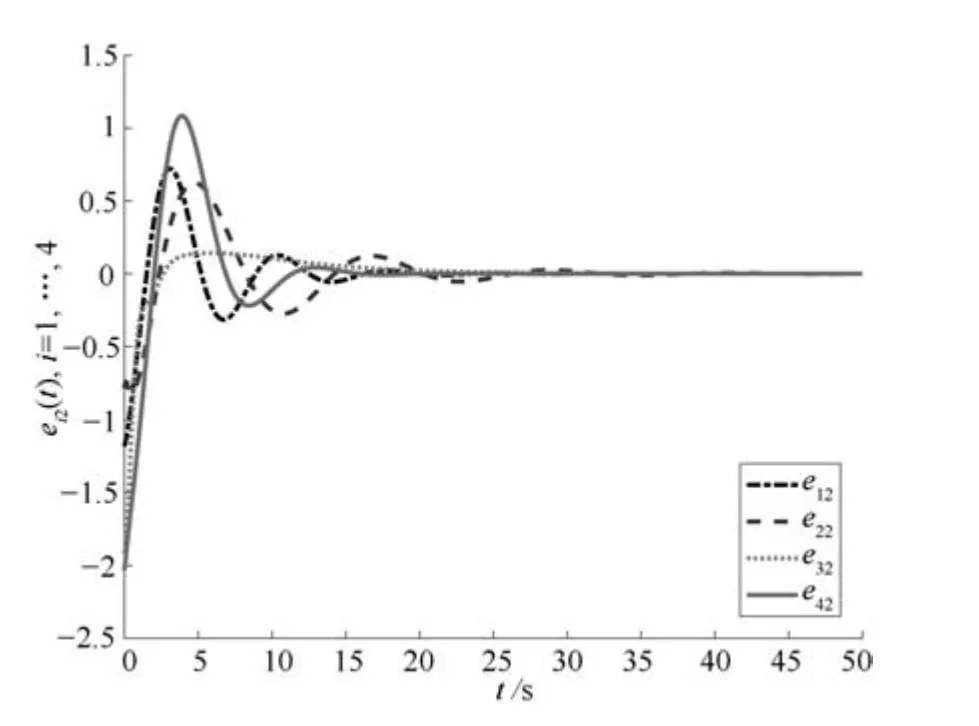
图5 智能体的调节输出ei2(t), i=1,2,3,4Fig.5 Regulated outputs ei2(t), i=1,2,3,4

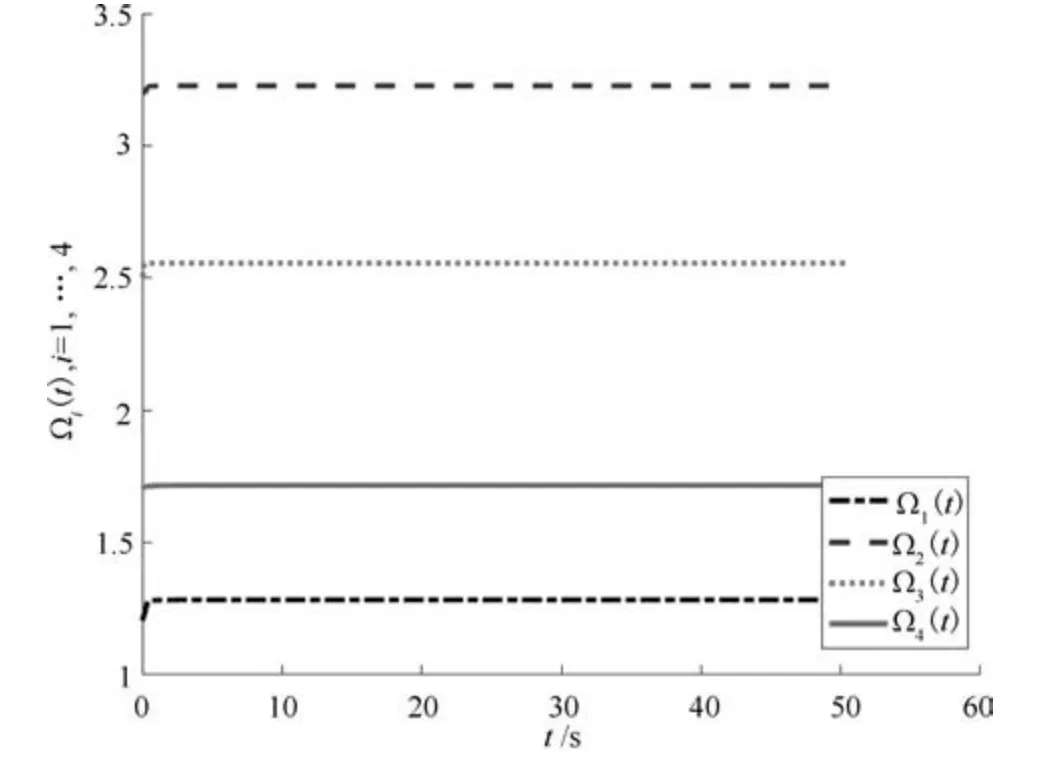
图6 控制器的自适应参数Ωi(t), i=1,2,3,4Fig.6 Adaptive parameters of the controllers Ωi(t),i=1,2,3,4

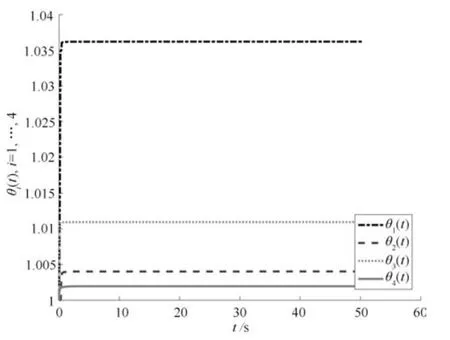
图7 自触发条件的自适应参数θi(t), i=1,2,3,4Fig.7 Adaptive parameters of the self-triggered conditions θi(t), i=1,2,3,4