基于透视投影下空间光照一致性分析的图像拼接篡改检测

张 旭 胡晰远 陈 晨 彭思龙

在照片发明的初期,由于需要经过专业的工序才能变更冲印内容,因此作为现实场景的记录方式,照片被视为有说服力的法庭物证.但是随着数码相机、手机等电子拍摄工具的普及,人们可以随时随地的拍摄各种数字照片;在互联网高度发达的今天,人们又可以随时将照片上传到网上或者从网上下载各种各样的图片;各种图像编辑工具的推出,普通用户就可以轻而易举地对图像进行各种操作;随着图像处理技术的不断增强,特别是机器学习方法的应用让计算机生成图像越来越逼真[1].这一切都使得人们对看到的图像不再深信不疑.其中,将一个人的头像从一张照片中抠取并粘贴到另一张照片中,制造该人参与第二张照片所呈现的事件的假象,是最常见的一类人脸图像篡改.

出于娱乐和美观等目的来修改图像,丰富了人们的生活;但是为了商业、政治等利益或者出于敲诈勒索等目的而恶意篡改图像,就会侵犯人们的名誉和财产[2].如图1 所示,据英国《每日邮报》2015年1 月24 日的报道,ISIS 公布杀害日本人质视频用以制造国际舆论.由于两个人质间无论是面部光照方向及地面阴影方向都有明显差别,鉴定专家认为ISIS 发布的视频是利用不同影像拼接得到的.根据《最高人民法院关于适用中华人民共和国刑事诉讼法的解释》中第九十二条规定:对视听资料有疑问的,应当进行鉴定.用来检测图像篡改的图像取证技术已成为证据科学领域一个重要研究方向.

图1 被质疑造假的日本人质视频截图Fig.1 The photo of Japanese hostages which is considered as a spliced image

由于篡改手段的多样性和隐蔽性,影像取证是公安司法部门在信息安全和司法物证领域中面临的技术难题.对于拼接篡改来说,由于不同照片的相机参数和所记录场景的物理几何特性存在差异,在不同照片进行拼接合成的过程中,很难做到完全一致.因此已有的研究从图像视频的成像过程、拍摄场景的真实性以及篡改手段的特定痕迹等入手,对拼接篡改进行取证,提出了众多的取证方法.图像取证领域的学者Farid 教授将这些方法进行归纳为5 类:基于像素插值、图像格式、相机噪声、场景物理特性和成像几何特征的方法[3].前三类通过检测重采样[4]、JPEG 格式有损压缩[5]和传感器模式噪声[6]等图像篡改过程中引入的数字属性变化来揭示数字图像篡改.近几年,深度学习技术在图像取证领域取得的一些应用成果[7],也多是基于这些数字属性特征进行图像分类.但是,由于许多原始数字属性随着照片的冲印也一并受到损失[8],使这些方法失去作用.然而照片内容却可以很大程度的保留和复现,因此基于图像内容的物理属性和几何特征的方法就成了研究的热点.基于运动模糊[9]、透视失真[10−11]、光照色彩[12]、眼睛高光[13]、阴影[14−16]、光照环境[17−21]、色温[22]、色彩纹理[23]等各种篡改检测方法,都在相关的实战案例中得到了成功应用.但是各种方法都有各自的局限性,只有存在适当的应用条件,才能提供具备说服力的证据.

其中,作为场景的基本自然物理条件,光照环境是检测图像篡改的重要手段.Kee 等[16]利用光线沿直线传播的特点,通过若干阴影点和对应的物体点的几何关系,分析图像不同物体间的光照方向是否一致.如果照片中没有足够的投射阴影,也可以利用不同物体反映的光照参数是否一致来检测是否存在拼接篡改.对于单一无限远光源,Johnson 等[17]假设在在平行投影下,物体遮蔽线处法向量同照片垂直的z轴方向分量为0,遮蔽线各点的垂线就是其法向量,得到2 维光照方向.如果辅以若干知道3 维法向量的点,就可以计算3 维光照方向.Carvalho等[18]基于用户交互,通过用户的经验标定出物体上一些点的3 维法向量,进而得到物体3 维光照方向.对于有多光源的复杂光照,Johnson 等[19]利用球谐光照模型来求解全局光照环境,扩展了光照估计的适用范围.这些光照估计方法都基于无穷远光源、朗伯体漫反射表面、凸物体以及表面反射率恒定等假设.

对于人脸照片的拼接篡改检测来说,因为有多种途径可以获取3 维人脸结构,可以更加方便地进行估计光照:扫描仪可以精确地得到人脸3 维点云,但是由于设备要求较高,限制了使用范围;而一些3 维重建技术比如3DMM (3D morphable model)[24],可以优化得到较为精确的人脸表面法向量.FaceGen 就是基于3DMM 的一个开放软件,但是重建人脸需要正面无表情人脸,并不能满足实际应用需求.而Zhu 等[25]利用King[26]检测的68 个人脸标定点,对不同姿态不同表情的人脸图像,都可以重建模型.虽然该方法的重建精度没有扫描仪和3DMM 算法高,但是由于没有较高的使用限制条件,也成了人脸篡改检测的一个得力工具.利用重建的人脸,Kee 等[20]在估计人脸姿态后计算对应的光照参数.Peng 等[21]考虑了人脸的非凸结构存在光照自遮挡现象以及眉毛等纹理反射率同皮肤不一致的问题,放宽了约束条件,提出了改进的光照估计算法.利用上述方法分析图1 中的日本人质的照片,都会得到和专家意见相似的分析结果.

但是,正如文献[17]用到的平行投影假设,多数方法同样是基于平行投影的假设来估计光照方向.如果将在投影平面上得到物体正面投影时物体对应的坐标系作为物体坐标系,那么,在平行投影下,各物体坐标系和相机坐标系平行,用来估计光照的法向量是图像中每个物体在各自的坐标系中旋转到对应姿态得到的法向量,等同于在相机坐标系中的法向量.但是由于相机成像模型是透视投影的针孔模型,得到正面投影时,物体其实是朝向相机光心的,各物体坐标系不再和相机坐标系平行,如果仍然按照平行投影处理,利用物体坐标系下的法向量估计的物体坐标系光照必然和相机坐标系光照有着明显误差.但由于人脸和相机距离超过1 米后,透视效果明显减弱,近似于平行投影,因此得到的相机参数存在显著误差[20−21].通过这些方法估计出的光照,即便差别很大,也仍有可能是真实的照片.所以,因为照片中光照方向不一致而被质疑造假的日本人质照片,如图1 所示,需要被重新审视.

为了克服这种误差,本文提出了一种透视投影下物体的空间光照估计算法,并通过各物体的空间光照一致性对图像拼接篡改进行检测.本文后续的内容安排如下:第1 节介绍了光照模型和光照估计算法的原理;第2 节分析了投影方法对光照估计的影响;第3 节详细地描述本文提出的算法;第4 节给出实验比较和分析;第5 节为全文的结论.

1 光照模型和光照估计算法概述

如图2 所示,在光照参数为l的场景光照L的作用下,人脸上法向量为N的顶点X0会反射部分光E进入相机,生成2 维图像I,其中X0的对应投影点为x.通过人脸扫描或者三维重建得到的3 维人脸结构X后,就可以利用若干顶点的亮度信息b和其他信息组成的矩阵M,估计光照参数l.其中,过程(1)是光照模型,(2)是相机模型,(3)是人脸模型,(4)是光照估计.前面三个模型是光照估计的基础,特别是光照模型,为光照估计提供了理论依据.此前,研究人员提出了许多不同的光照模型.其中,由于人脸近似于反射率为ρ的漫反射朗伯体表面,因此在光照估计算法中常用的两个模型是Lambert模型[27]和球谐函数SH 模型[28−29].Lambert 模型可以较好地表现类似阳光的简单光照,而SH 模型对具有多光源的现实场景中的复杂光照也可以很好地表现.

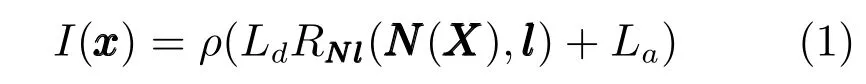
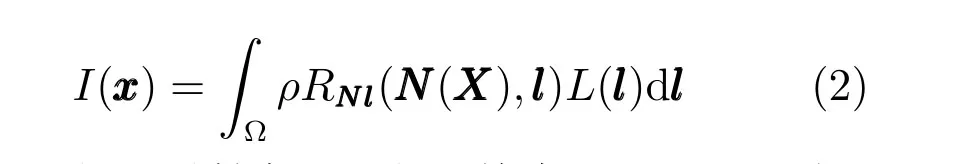
其中,Ld是漫反射光,La是环境光,RNl 同N 和l之间的夹角θ有关,且限定不小于0,因为在该顶点背后入射的光线不会到达该顶点,所以可以表示如下:

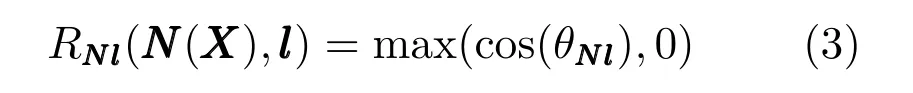
考虑到人脸的纹理信息ρ和结构信息G(如果物体是朗伯体,纹理ρ就是一个常数;如果是凸物体,结构G就等于1),光照模型的原理可统一为如下形式:

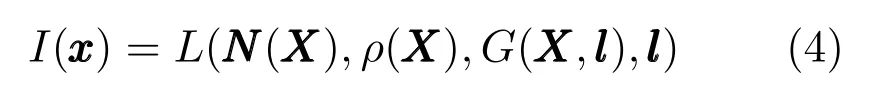
如果将人脸各点的法向量、纹理、结构等信息用矩阵M(X)表示,那么就可以用矩阵形式描述人脸图像各点亮度b(x):

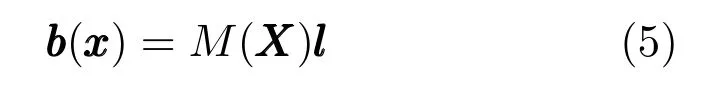
其中,l和M(X)在不同的光照模型中有不同的形式,具体可以参考文献[17−21].

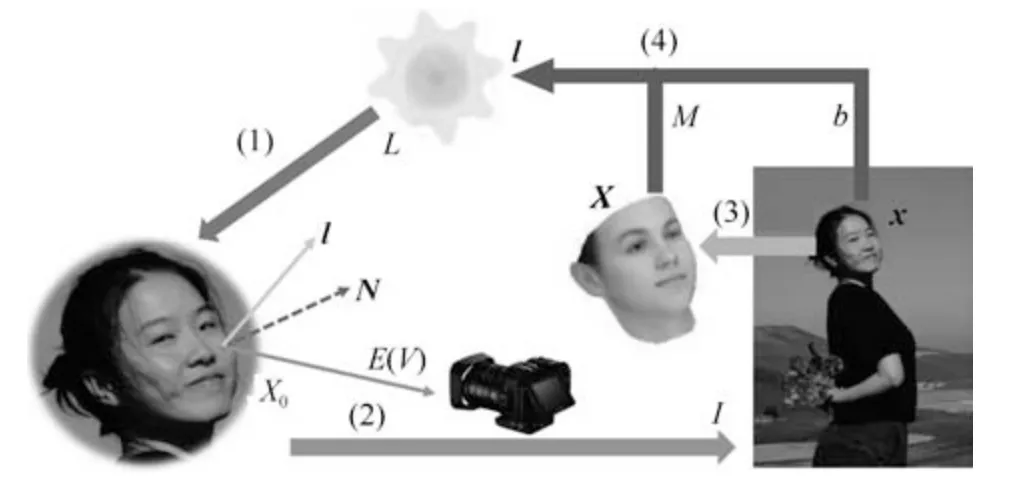
图2 光照模型和光照估计原理图Fig.2 The principle of Illumination model and lighting estimation

给定一张人脸图像I,就知道了图像中各点的RGB 亮度值b.如果知道图像上若干点的法向量和纹理、结构信息得到矩阵M,就可以通过最小二乘算法来估计光照参数l:

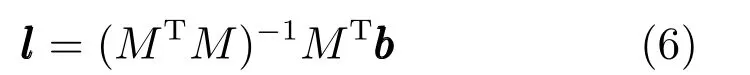
因为Lambert 模型和SH 模型中l分别有4 个和9 个参数,因此估计光照至少需要4 个或9 个点.文献[17−21]中的光照估计方法可统一为如下形式:

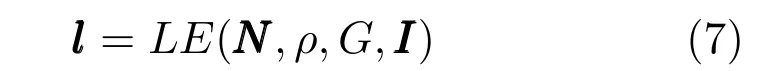
估计出图片中不同物体的光照参数l后,文献[17−21]通过光照参数之间的差别d(lij)来判断光照是否一致:

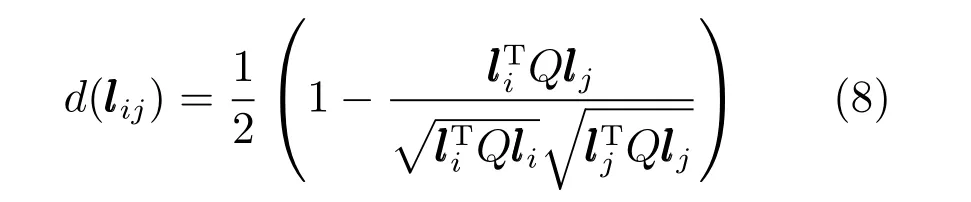
其中,对于SH 模型,Q是9×9 矩阵,具体形式可以参考文献[19];对于Lambert 模型,则可以认为Q=1,直接计算光照方向的差别.

如果单纯利用人脸皮肤区域和人脸凸区域的情况下,光照估计的关键就是得到人脸上各点较为精确的法向量N.此前多数方法都是基于平行投影的假设来估计光照.而我们知道相机成像模型针孔模型是透视投影,下面我们将分析投影方法的不同会对法向量N和估计的光照l造成哪些影响.

2 投影方法对光照估计影响的分析

2.1 平行投影和透视投影

图3 是平行投影和透视投影下光照差异的示意图,左边为平行投影,右边为透视投影.其中,外围实线框是成像平面,外围虚线框是对应的空间视野.约定垂直于照片向里为相机坐标系z轴正方向(光轴),坐标系满足右手螺旋定理.相机坐标系Cc和照片平面垂直,用向上虚线箭头表示.初始人脸坐标系Cf0同Cc一致,对应的初始法向量为Nf0,是头顶朝下面朝里的人脸.将Cf0绕x轴翻转180 度得到和光轴相反的坐标系Cf,此时人脸姿态是头顶朝上的正面人脸Pf,对应的正面法向量为Nf=RfNf0,其中Rf=[1,0,0;0,−1,0;0,0,−1]为对应的旋转矩阵,称为正面姿态矩阵.投影平面上物体正面投影对应的坐标系为物体投影坐标系Cp,用实线框中朝下的虚线箭头表示其z轴正方向,Cp和Cf保持平行.物体在Cp中也就是照片中的姿态Pp用实线框中实线细箭头表示,对应的投影法向量为Np=RpNf,Rp为Pp和Pf间的旋转矩阵,称为照片姿态矩阵;此时物体在场景空间中的实际姿态Ps用虚线框中实线细箭头表示,在Cc中对应的空间法向量为Ns=RsNf,Rs为Ps和Pf间的旋转矩阵,称为空间姿态矩阵.得到物体正面投影时物体对应的空间坐标系定义为物体正面坐标系Cd,用虚线框中虚线细箭头表示其z轴正方向,物体在Cd中的姿态Pd同物体在Cp中的姿态Pp保持一致,对应法向量Nd=Np.利用式(6)和(7),得到Np和Ns对应的照片投影光照lp和实际空间光照ls:

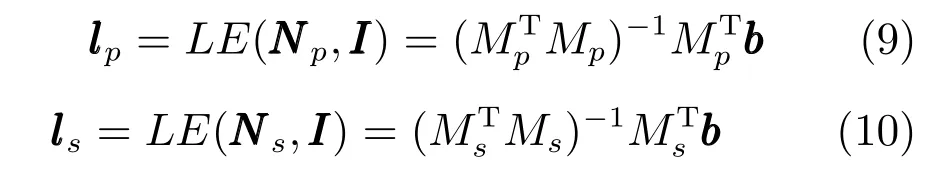
那么,在平行投影下,Cd和Cp互相平行,Rs同Rp相同,投影到成像平面后,Ps和Pp一致:

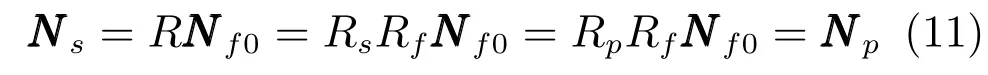
可以看到,在平行投影的假设下,Ns=Np,对应的ls=lp.也就是说,各物体在照片中的投影光照(图3(a)中实线框中实线粗箭头),就是它们在场景空间中的实际光照(图3(a)中虚线框中实线粗箭头).

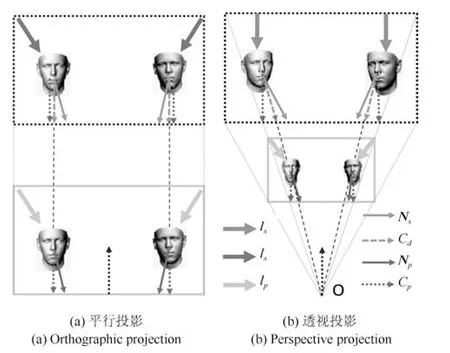
图3 平行投影和透视投影对光照估计的影响示意图Fig.3 The influences of the projection methods on the lighting estimation

在透视投影下,只有面朝光心O的人脸才能在成像平面上得到正面人脸.当人脸不在相机光轴上时,Cd和Cf不再平行,而是存在一定夹角,Rs和Rp不相等,投影到成像平面后,Ps和Pp不一致:

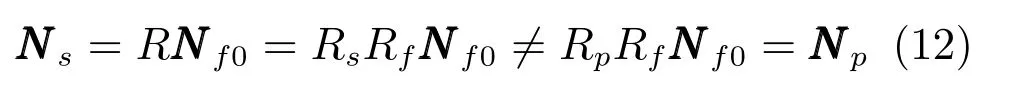
可以看到,在透视投影下,Ns=Np,对应的ls=lp.也就是说,各物体在照片中的投影光照(图3(b)中实线框中实线粗箭头),并不是它们在场景空间中的实际光照(图3(b)中虚线框中实线粗箭头).

由于相机模型是基于透视投影的针孔模型,因此照片中各人脸的投影姿态并等同于它们在空间中的实际姿态.同一张照片中不同物体投影光照存在明显差异的时候,在真实场景空间中仍有可能具有相同的光照参数.因此,我们需要在统一的坐标系下进行光照估计和比较,才能正确进行光照一致性分析.相机坐标系就是一个很好的选择.而本文所说的空间光照,也就是在相机坐标系下的光照.

2.2 经典相机标定在取证中的局限

对于相机针孔模型,从空间3 维点XXX到图像2维点x的映射关系为:

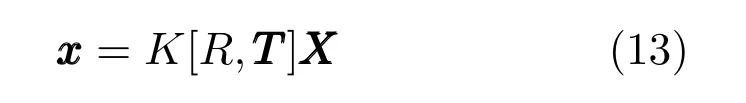
其中,K和[R,TTT]分别是相机的内参和外参矩阵.其中,R是相机坐标系和物体坐标系间的旋转矩阵,可以参数化为欧拉角(α,β,γ);TTT是两坐标系间的平移矩阵,表示物体坐标系原点在相机坐标系中的坐标(Tx,Ty,Tz)T.内参矩阵K形式如下:

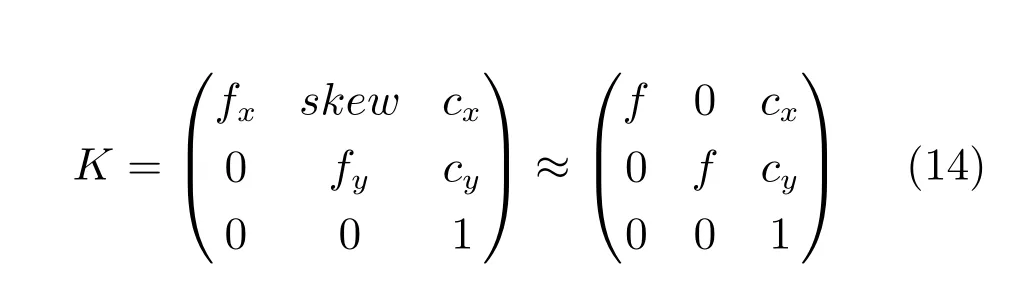
其中,(cx,cy)是相机主点,fx和fy分别是图像水平和竖直方向上的像素单位焦距,skew是元器件斜度.一般情况下认为fx和fy都等于f,同时skew为0.

将上述参数组成一个9 个未知参数的向量,定义为透视参数σ=(f,cx,cy,α,β,γ,Tx,Ty,Tz)T,其中,σex=(α,β,γ,Tx,Ty,Tz)T为外参,σin=(f,cx,cy)T为内参.这样,式(13)可表示成:

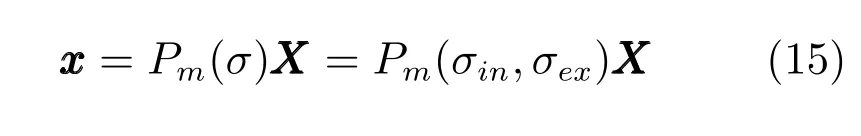
Pm是由σ决定的映射矩阵,求解Pm的问题就是相机标定问题.构造nd个图像点ximi和对应XXXi的投影点xi之间的误差函数:

应用Levenberg-Marquardt 方法就可以求解.

相机标定求解的精度依赖于XXX的精度以及XXX和xim的配准精度.传统的相机标定方法使用标定板[30]、规则几何图像[31]进行标定,标定精度高,但往往不会出现在待鉴定的篡改图像中.对于人脸来说,文献[20−21]利用图像中人脸标定点xim和人脸3 维模型点XXX的约束关系来求取映射矩阵.表面上,上述两个条件都可以将误差控制在允许范围内,得到可以接受的映射矩阵.但是,如图4(a)所示,随着人脸中心和相机中心距离的增加,透视效果明显减弱,在超过1 米后,人脸投影几乎保持不变,图4(b)中可以看出无穷远下的关键点和它们在透视人脸上的对应点之间的距离误差急剧下降,因此在人脸相机间的距离超过一米后,通过关键点估计的相机参数就会存在显著的误差.事实上,估计出的焦距ˆf趋近于一个无穷大的值,接近于平行投影,而估计出的旋转矩阵ˆR对应的人脸姿态Ps则非常接近于人脸投影姿态Pp,得到的光照仍然近似于照片投影光照,也就是平行投影下的光照,ls ≈lp:

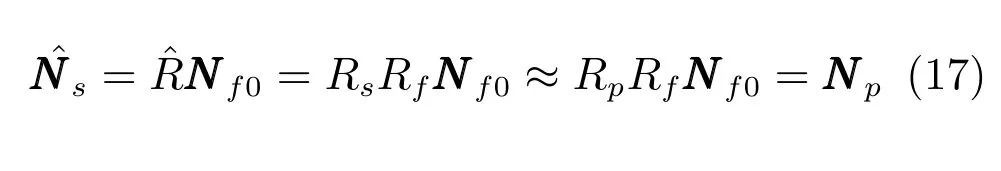
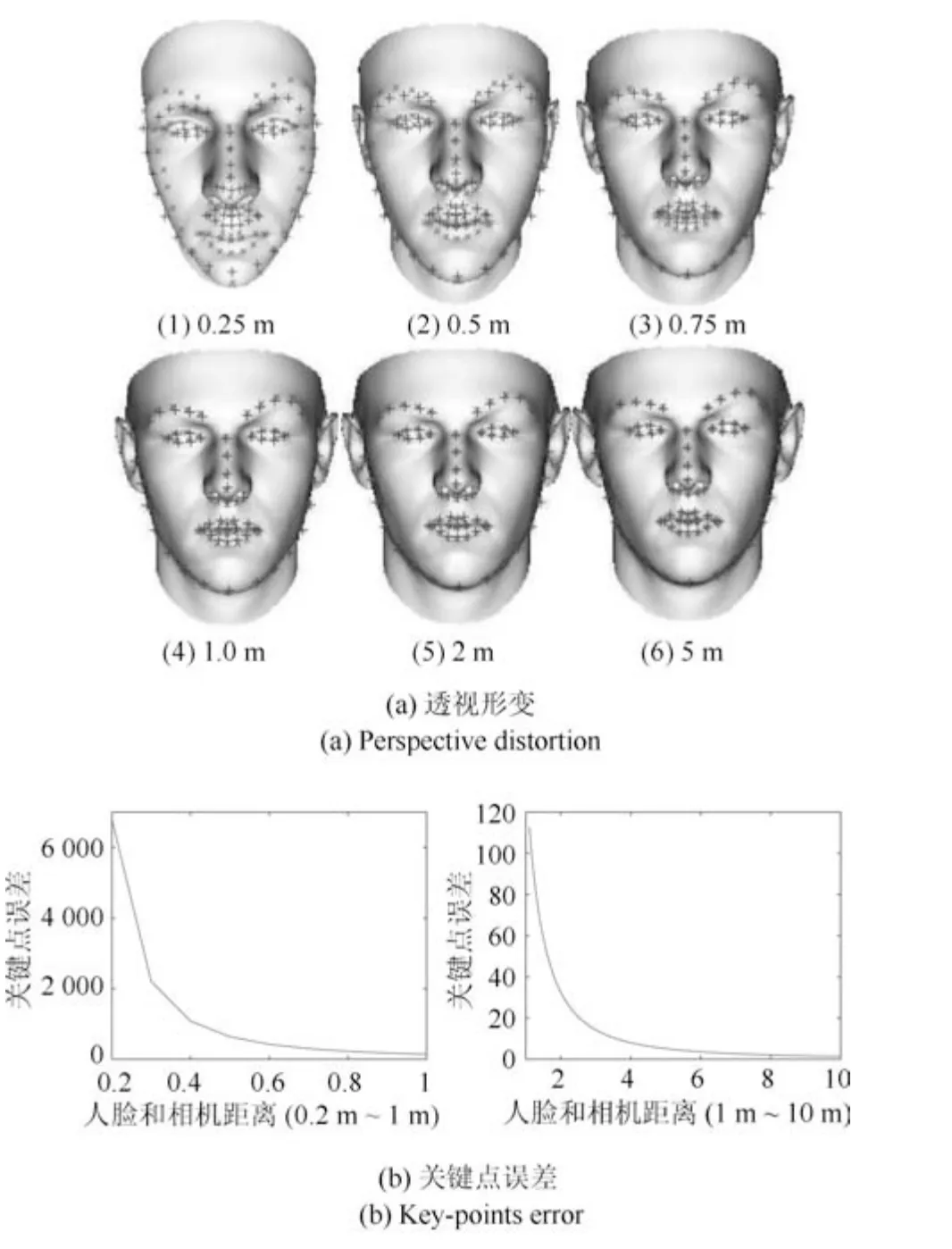
图4 人脸透视形变程度随人脸到相机距离变化的情况Fig.4 The influences of the distance from the face to the camera on the facial perspective distortion

总之,由于相机模型是基于透视投影的针孔模型,而且多数照片中人脸距离相机都超过1 米,因此,之前基于平行投影假设或者根据人脸关键点标定相机后进行光照估计的算法,会错误地将各人脸在照片中的投影姿态Pp作为空间中的实际姿态Ps,因而利用投影法向量Np计算得到的光照是照片投影光照lp,而不是具有统一坐标系的空间光照ls.如果直接根据投影光照进行一致性分析,就会由于原理上的错误而得到错误的判断结果.接下来,我们将阐述如何得到相机坐标系下的空间法向量Ns,进而得到空间光照ls的方法.

3 本文算法

在已有光照估计方法的基础上,本文提出了一种基于透视投影下的空间光照估计方法,其算法流程可分为5 个步骤,如图5 所示:1)利用文献[26]中的算法检测68 个人脸标志,并利用文献[25]中的方法重建待分析人脸3 维模型;2)计算照片中人脸模型Nf0、人脸投影姿态矩阵Rp、人脸中心投影位置h和照片姿态下的投影光照lp;3)通过经典方法或者本文提出的优化方法进行相机标定,求得透视参数;4)用透视参数ˆK得到相机坐标系下的人脸空间法向量Ns,进而求得空间光照ls;5)利用所提出的判定依据对照片人脸空间光照及其他空间信息的合理性进行分析.其中,图5 中第2 步和第4 步的图从上到下依次为用于计算光照的姿态、估计的光照渲染球以及透视参数下人脸的重投影图像.

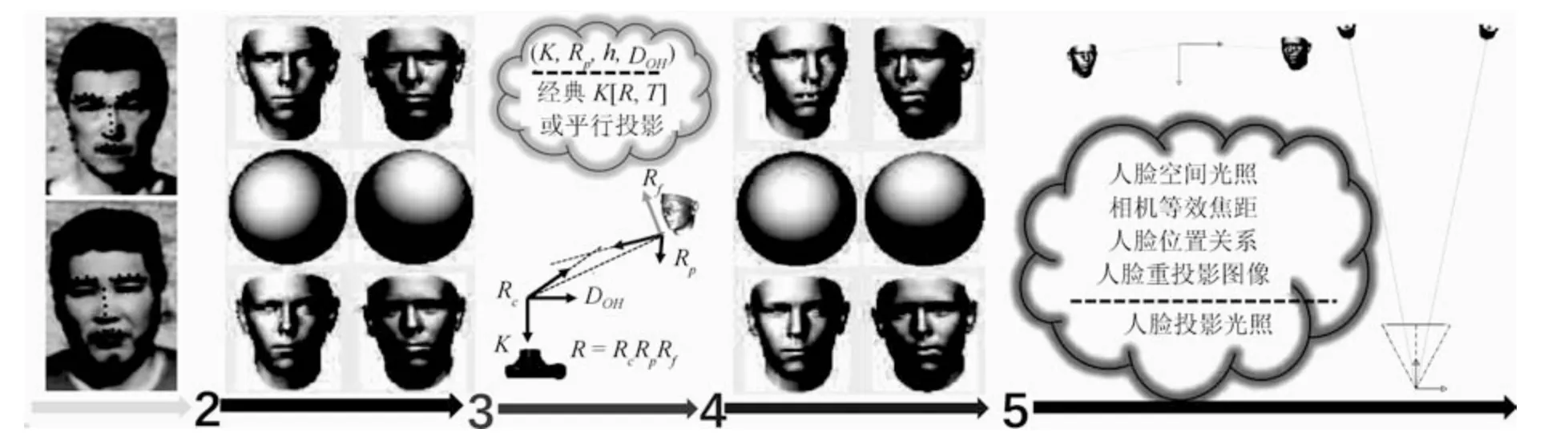
图5 算法流程图Fig.5 The workflow of the proposed method

3.1 新的旋转矩阵求解方法

通过第2 节的分析,我们知道相机内外参数估计的精度影响着在相机坐标系下物体空间光照参数的估计准确度.但是经典的标定方法又不能胜任多数人脸图像篡改的案例.然而,第2 节的分析给了我们启发:既然可以较准确地得到照片中人脸的姿态Pp,它和人脸在空间中的实际姿态Ps有什么关系呢？

如图6 所示,将人脸中心在相机坐标系中的空间位置定位为H,H同相机光心O之间的连线定义为OH,OH的长度DOH就是人头距离相机光心的距离.在照片中投影得到正面人脸的人脸坐标系Cd的z轴就和OH重合并指向光心O.固定O、H和人脸姿态Pd,无论相机如何转动,焦距如何改变,投影在成像平面上的人脸模型3 维点都是固定的同一簇射线.因此人脸在成像平面上的投影图像的姿态Pp始终等于Pd,改变的只是投影图像的位置、大小和形变.我们将相机光轴同OH之间的旋转矩阵称为相机姿态矩阵,并用Rc来表示.可以看出,Pp和Ps之间的关系就是Rc,Pp经过Rc旋转得到Ps,有Ns=RcNp.相应的,Rs=RcRp,因此相机和人脸之间的旋转矩阵R就可以表示为:

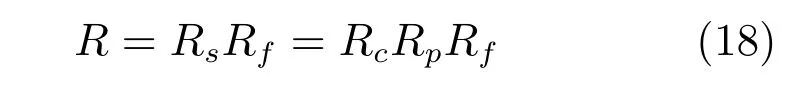
3.2 计算相机姿态矩阵

给定一张照片,照片中人脸中心定义为h=(hx,hy,1)T.那么就可以得到位于OH上、z轴坐标H1z=1 的空间点H1的坐标:

从O指向H1间的向量定义为vOH1=(H1x,H1y,1)T.和光轴平行的单位向量定义为vOA=(0,0,1)T.通过计算vOA和vOH1间的旋转矩阵求得相机姿态矩阵Rc.

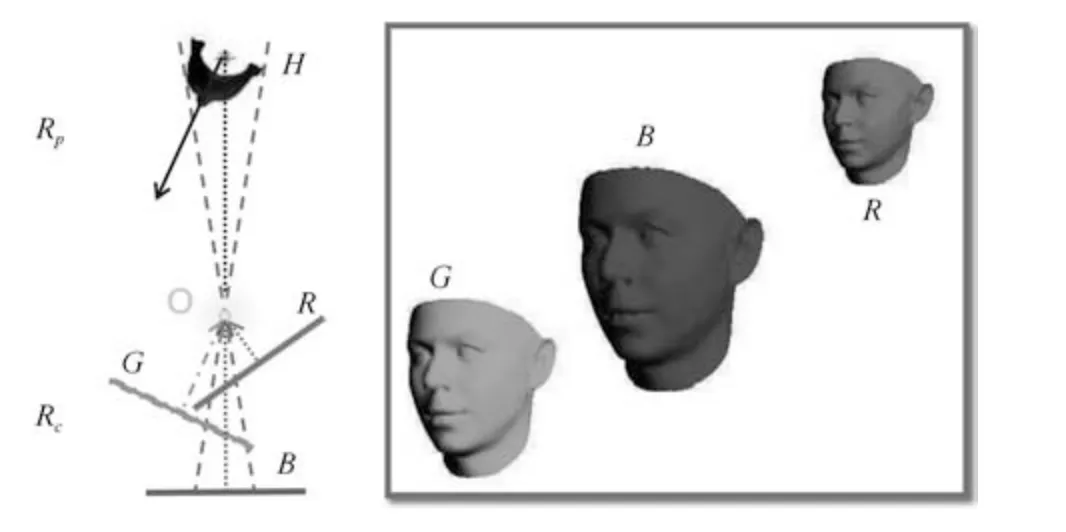
图6 固定人脸和相机光心,人脸的照片姿态就保持不变,不随相机焦距变化和姿态旋转而变化Fig.6 The poses of the face in the photo remain the same once the face and the optical center are fixed

给出任意两个单位向量vf=(vfx,vfy,vfz)T和vt=(vtx,vty,vtz)T,从vf到vt的旋转矩阵Rft可以通过Rodrigues 旋转方程计算得到,如图7 所示.首先,可以计算得到垂直于vf和vt所在平面的旋转轴oft=vf ×vt=(ox,oy,oz)T.vf和vt之间的夹角θft=arc cos(vf ·vt).用s表示sin(θft),用c表示cos(θft),用b表示(1−c),并用oij表示oi×oj.那么,Rft(vf,vt)可以表示为:

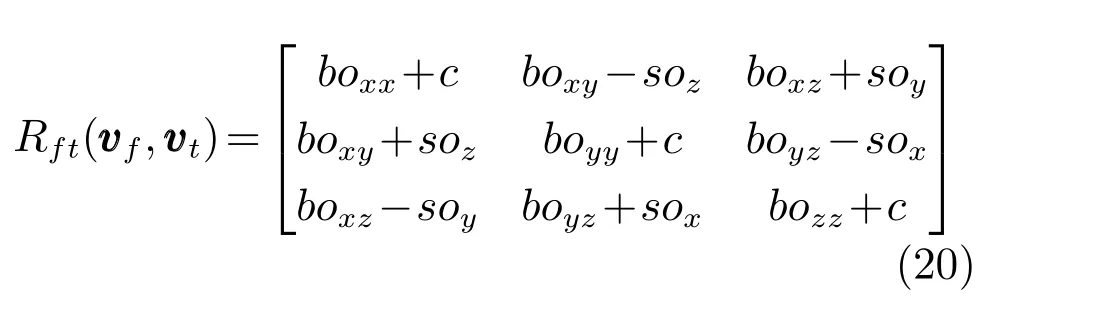
利用式(20)可以得到相机姿态矩阵Rc:

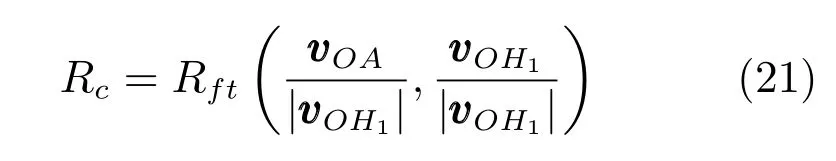
可以看出,Rc是关于K和h的函数.

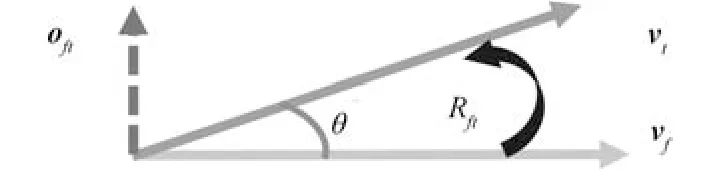
图7 Rodrigues 旋转公式的示意图Fig.7 The principle of Rodriguesrotation formula

3.3 空间光照的估计

现在,利用式(12)、(18)、(21),图像中第i个人脸在相机坐标系下的空间法向量Nsi就可以表示为:

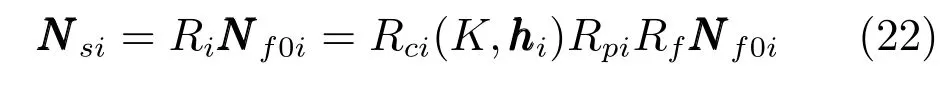
然后利用Nsi求的Ms,通过式(10)就可以得到空间光照lsi:

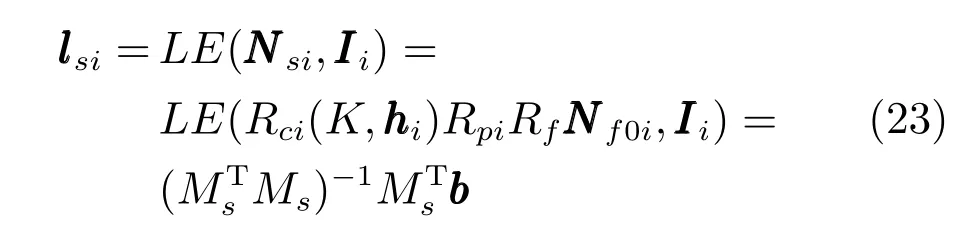
这样,不同人脸的光照就被统一到了相机坐标系下.通过重建的人脸3 维模型Nf0、估计的照片姿态矩阵Rp、照片中人脸中心的位置h以及人脸图像I中皮肤的RGB 亮度值b,只要知道相机内参矩阵K,就可以得到相机坐标系下各人脸的人脸空间光照,然后进行空间光照一致性分析.

相机内参矩阵K可以利用照片中的规则几何标定得到,或者从照片的可交换图像文件格式(Exchangeable image file format,EXIF)中获取精确的相机焦距.如果照片中没有有效的信息可以计算相机内参,我们就可以通过照片中不同人脸的空间光照一致的约束,得到使空间光照lsi和lsj之间差别d(lsij)(式(8))最小的相机参数:

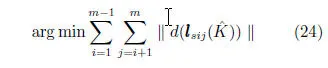
空间光照估计算法具体步骤如下:

步骤1.输入为照片中m个人脸对应的3 维点法向量Nf0,估计的照片姿态矩阵Rp,图像人脸中心的位置h以及图像人脸皮肤的RGB 亮度值b;

步骤2.如果相机内参K已知,通过式(19)得到各个人脸的图像中心点h对应的空间位置H1;

步骤3.通过式(21)计算各个人脸的空间位置H1对应的相机姿态矩阵Rc;

步骤4.通过式(23)计算各个人脸的空间光照ls;

步骤5.如果相机内参K未知,则计算两两人脸之间的空间光照差别diff(lsij),求解优化方程(24),收敛或者达到迭代次数后,输出相机内参K以及各物体的空间光照ls.

3.4 人脸空间坐标

相机坐标系Cc中空间人脸中心坐标H=[Hx,Hy,Hz]T可以通过下式得到:

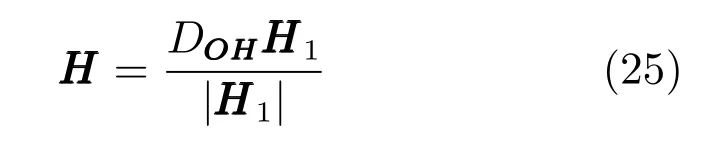
可以看出H关于K,h和DOH的函数.得到图像中各人脸在相机坐标系下的位置坐标,就可以将相互位置是否合理作为判断图像合理性的一个辅助依据.

给定一张人脸照片,式(13)可以写成:

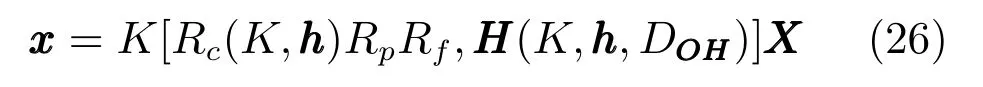
同样的,式(15)可以写作如下形式:

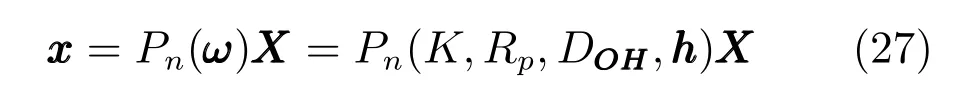
其中Pn是由ω决定的一个新的映射矩阵.由于Rp和h可以较为准确地从人脸图像中得到,因此式(27)中就只有K和DOH未知,ω是包含4 个未知数[f,cx,cy,DOH]T的向量.利用光照一致性优化得到的ˆK,就能估计出DOH的大小:

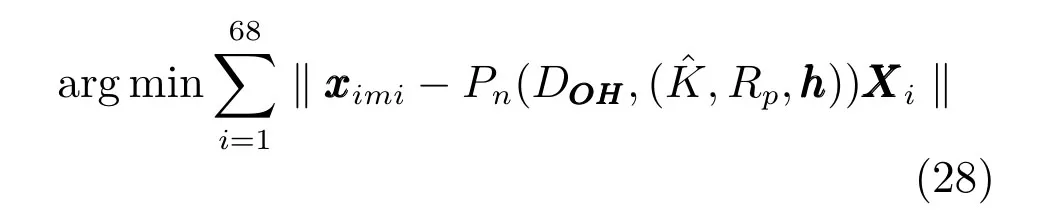
经典的相机标定方法将物体坐标系原点TTT=(Tx,Ty,Tz)T作为参数一起估计,即便DOH固定,TTT仍然随着旋转矩阵R的变化而变化.相比于经典方法,式(27)将DOH作为估计参数独立于旋转矩阵而存在,再加上未知参数数目从9 个减少为4 个,针对人脸的标定问题,该方法更容易得到鲁棒的解.

3.5 等效焦距EFL

由于之前基于光照的取证方法无法获得较为精确的焦距,因此对焦距的研究很少.本文简要介绍焦距的一个常识性概念,等效焦距(The equivalent focal length,EFL).不同的相机传感器有不同的尺寸,例如,索尼和尼康Dx 中使用的APS-C 的宽度、高度和对角线长度分别为22.3 mm、14.9 mm和27.3 mm,而iPhone 6 中使用的1/3CMOS 的相应尺寸分别为4.8 mm、3.6 mm 和6.0 mm.为了便于比较性能,人们使用全帧胶片的对角线长度43.4 mm 作为参照标准来计算其他传感器的等效焦距.其相关尺寸分别为36 mm、24 mm 和43.4 mm,如图8 所示.对角线尺寸为XX mm 的传感器,其转换系数rd=43.4/XX,等效焦距=物理焦距× rd.同样,我们可以将计算得到像素单位的焦距f转换为mm 单位,使用照片主点c(cx,cy)和照片的4 个顶点vim之间的最大长度得到等效焦距Feq:

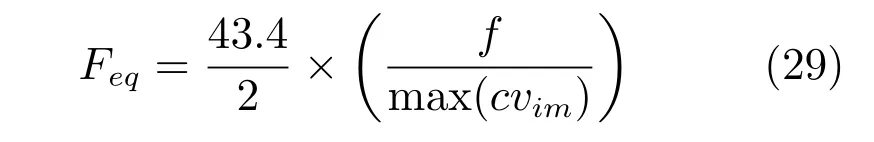
这样,我们就能利用优化得到的等效焦距范围是否合理,作为图像是否被篡改的一个辅助证据.等效焦距越小,视野越大,图像靠近边缘形变越明显,属于广角镜头;等效焦距越大,视野越小,图像靠近边缘形变越不明显,属于长焦镜头,越接近平行投影.

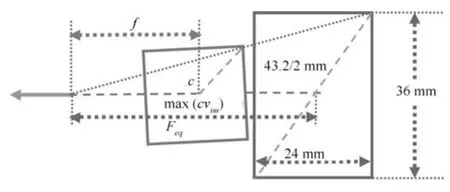
图8 等效焦距示意图Fig.8 The illustration of equivalent focal length

3.6 空间合理性指标

传统的光照估计方法只能得到平行投影光照lp,然后只能根据两个光照lpi和lpj之间的差别d(lpij)的大小来进行光照一致性分析进而检测图像篡改.但是根据分析,d(lpij)差别大并不能说明问题,同时传统的方法也只有投影光照可以用来分析,因而传统光照分析方法得到的结果明显具有局限性.

本文利用上面章节计算的信息对待检验照片进行空间信息合理性分析,包括空间光照ls、相机等效焦距Feq、人脸位置关系DH和人脸重投影图像Ire.

1)空间光照ls:得到图像中各人脸的空间光照ls后,就可以根据式(8)计算第i和j个人脸的空间光照差别d(lsij).同lp相比,ls是各人脸统一到相机坐标系下的光照,用来描述人脸光照是否一致具有更高的准确度;

2)相机等效焦距Feq:普通的数字相机和手机都有常见的焦距范围,如果Feq明显过小或过大同拍摄设备不符,就可以说明问题.另外,等效焦距越小,视野越大,图像靠近边缘失真越明显,属于广角镜头;等效焦距越大,视野越小,图像靠近边缘失真越不明显,属于长焦镜头,越接近平行投影.如果估计的Feq和图像中人脸失真程度不符,也可以说明问题;

3)人脸位置关系DH:通过式(25)可以计算每个人脸的空间位置坐标,进而可以得到人脸同相机的距离DOH以及人脸之间距离DHH.如果同照片展示的物理事实有明显不符,就可以说明问题,比如互相靠近的两人间的距离过大;

4)人脸重投影图像Ire:通过式(15)和(27)可以将人脸模型Nf0按照估计的相机参数重新投影,如果重投影图像Ire和照片中的图像差别过大,就可以说明问题.

4 实验结果及分析

4.1 真实图像分析

我们首先使用一张晴天时拍摄的一个18 人足球队的原始照片来验证我们提出的方法,如图9 所示.这张照片是用华为P9 Plus 拍的,它的传感器是1/2.9英寸的索尼IMX 286,物理焦距是4 毫米,等效焦距是29 mm.按照算法流程,首先提取标定点并重建三维人脸模型.由于位于后排中间的运动员佩戴运动眼镜的影响,无法正确标定人脸关键点和重建人脸模型,我们将他看做伪造人脸.图11 的第一个框中就是18 个队员对应重建人脸和投影光照渲染球.因为存在差别比较大的投影光照,按照投影光照进行判断,会认为这张照片的光线不一致.

图9 晴天下拍摄的一个足球队的真实照片Fig.9 A pristine photo of a football team taken on a sunny day to verify our proposed approach

假设图像主点位于图像中心,通过任意两个人脸和就可以优化得到对应的优化焦距和相应的空间光照ls.进而得到优化等效焦距、优化等效焦距和实际等效焦距的差别以及投影光照差别d(lpij)和该焦距对应的空间光照差别d(lsij).18 个队员两两计算,就得到这4 个变量长宽为18×18 的矩阵图,如图10 所示.

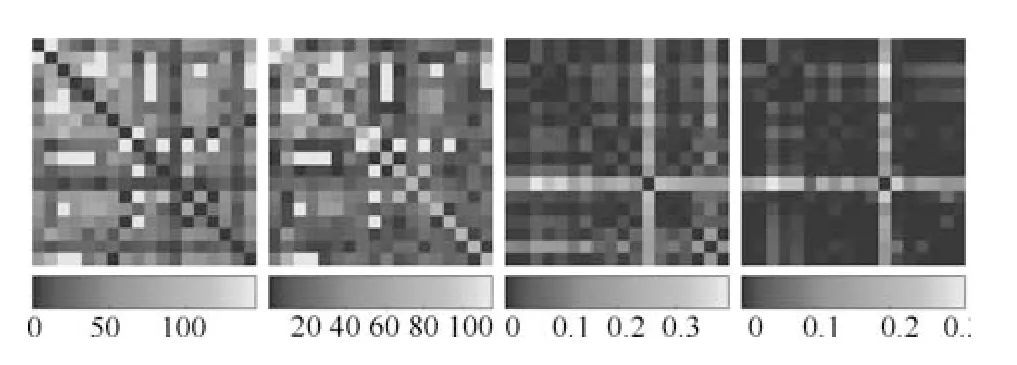
图10 图9 中任意两人优化的等效焦距及其和真实焦距的误差,投影光照差别及空间光照差别Fig.10 The maps ofbetween any two person in Fig.9

可以看出,优化等效焦距在有些情况下很接近实际等效焦距,有时差别较大.从整图来看,多数情况下d(lsij)都会比d(lpij)小,有时会小很多,说明即便单纯用投影光照lp和空间光照ls来进行一致性分析,统一坐标系的空间光照ls更能表征光照一致性.

接下来,我们对图中出现的几种主要类型进行分类说明:

1)当d(lpij)本身较大时,如果对应的和Feq较为接近,d(lsij)会明显小于d(lpij),其他信息也都合理.比如图11 中第二排框,通过(6,11)两人人脸估计透视参数,d(lp(6,11))=0.0219,d(ls(6,11))=0.0001.照片中其他人的空间光照也都变得比较接近,尤其是投影光照差别明显的人脸17和18.ˆFeq(6,11)=29.3 mm,和照片相比重投影模型没有较大形变,而且相互空间位置比较合理,没有过近或者过远,,如图12 第一列所示;

2)当d(lpij)本身较大时,如果对应的和Feq差别较大,d(lsij)并不明显小于d(lpij),其他信息合理性也很低,篡改的可能性就很大.比如图11 中第三排框,通过(3,12)估计透视参数,d(lp(3,12))=0.3508,d(ls(3,12))=0.3009,=5 mm,和照片相比重投影模型形变严重,而且相互空间位置过于接近,不符合实际,如图12 第二列所示;

图11 图9 中18 名队员的三维人脸模型和投影光照渲染球,以及三组通过不同人脸估计的透视参数对应的人脸空间姿态、空间光照渲染球及重新投影的人脸透视模型对比Fig.11 The 3D face models and projected lighting of the 18 players in Fig.9,and three groups of spatial pose,spatial lighting and re-projected face model under the estimated perspective parameters using three different pairs of faces

3)当d(lpij)本身较小时,对应的往往比较大,这是因为对于无限远空间光照来说,只有在两人和相机光心之间连线的夹角比较小时,投影光照才会比较接近,此时很难通过一致性约束得到准确的透视参数,所以便会得到长焦距,接近于平行光照,如果此时其他的信息合理性也低,那么图像的篡改可能性较大.比如图11 中第四排框,通过(5,10)估计透视参数,d(lp(5,10))=0.0063,d(ls(5,10))=0.0098,=115 mm,重投影模型虽然没有较大失真,但是相互空间位置过远,互相搭肩的两人距离超过了1 m,不符合实际,如图12第三列所示.

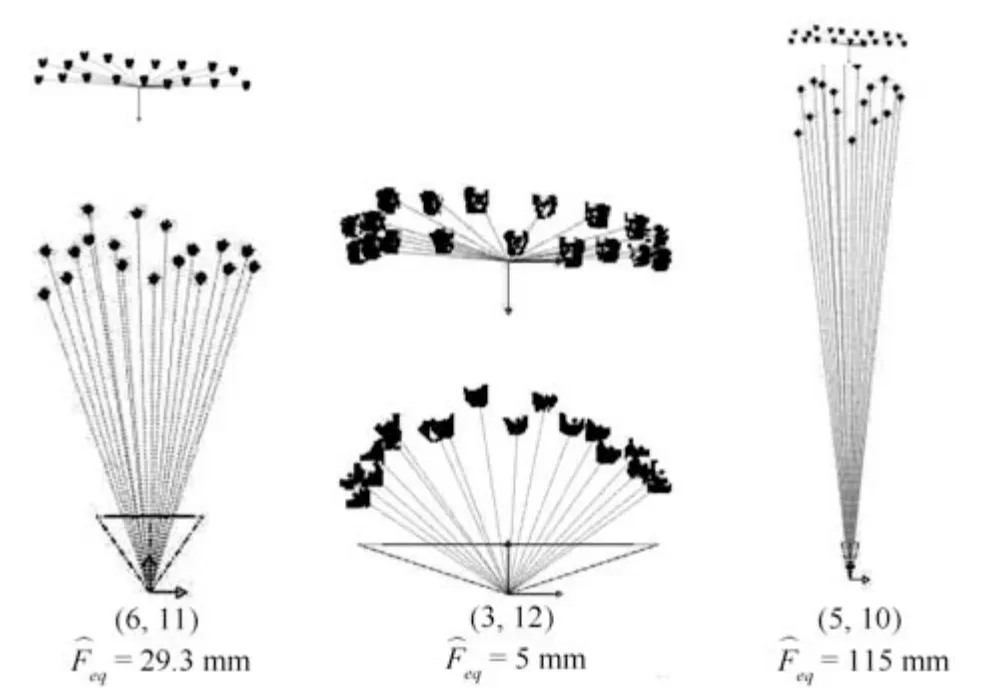
图12 根据人脸(6,11)、(3,12)、(5,10)优化得到的参数估计出在人脸空间分布(上方为正视图,下方为俯视图)Fig.12 The estimated spatial poses of 18 human faces according to the optimized parameters of human faces (6,11),(3,12)and (5,10),respectively (The first row is the face view,and the second row is the top view of the faces)

4.2 公开数据集实验

由于多数用于篡改检测的数据集中不包含人脸,而已有的人脸数据库,包括最近公开的基于深度学习的计算机生成人脸库ForensicsFaces[1],多是单一人脸.这些都不适用于评估本文算法.文献[12]公开了真实人脸拼接照片数据集DSO −1.由于DSO −1 主要用于评估该文提出的光照色彩估计算法,里面多数照片都是距离很近的合影,而且有很多是在非无穷远光源的室内光照和闪光灯下拍摄.我们主要选择一些晴天下拍摄的真实照片和拼接照片进行实验.下给出4 个例子,如图13 所示.

对于图13(a),传统方法会直接按照投影光照差别大d(lpa)=0.2463 判为篡改图像,如图中第二排虚线所示.本文算法无法得到将lpa优化成空间光照lsa差别足够小的透视参数,=125 mm,实际上lsa同lpa基本相等.可以判断这是一个篡改图像.

对于图13(b),d(lpb)=0.0093,传统方法会判为真实图像.由于d(lsb)非常小,本文算法无法得到合理的透视参数,=94 mm,而图中女生照片有明显的透视形变,说明相机等效焦距较小,因此是个篡改图像.实际上,由于闪光灯拍摄不符合无穷远光源的前提假设,不满足本文方法的空间光照一致性的约束,无法得到正确的透视参数.但是传统方法对闪光灯这种明显点光源的照片按照投影光照一致判为真实图像,其实从侧面说明了传统方法的局限.

图13 对DSO-1 数据集中的四幅样本图像的检测结果.(a)∼(d)分别是对拼接图像正确检测,对原始图像错误报警,对原始图像正确检测,对拼接图像错误检测Fig.13 The detection results of our method on four sample images in the DSO-1 dataset.(a)∼(d)are respectively a correct detection for splicing image,a false alarm for pristine image,a correct detection for pristine image and a miss detection for splicing image

对于图13(c),传统方法会按照d(lpc)=0.0635较大判为篡改图像.利用本文方法,得到优化的=20.2 mm 下的d(lsc)=0.0167,较d(lpc)有明显改变.同时,二者头部间距为0.24 m,距离相机都为1 米左右,比较符合照片的事实,是真实照片的合理性较大.

对于图13(d),传统方法会按照d(lpd)=0.1065较大判为篡改图像.利用本文方法,得到优化的=34 mm 下的d(lsd)=0.0361,虽然本身较大判断为篡改.但由于较d(lpd)有明显改变,同时,二者头部间距为0.69 m,距离相机分别为1.87 米和1.61 米,比较符合照片的事实,是真实照片的合理性较大.实际上这是一个篡改图像,如果可以从相机中读取准确的等效焦距,就可以进行比较.错误判断的一个原因可能是原始的两张照片是在相似的条件下拍摄的.

4.3 日本人质案例鉴定

现在,我们不能再因为图1 中日本人质照片的投影光照差别d(lp)=0.1327 足够大,就认为这张图片是篡改照片.按照本文方法,优化得到等效焦距=44 mm,相应空间光照差别d(ls)=0.0755虽然明显变小.两人空间位置分别是(−0.5556,0.1015,3.3071)和(0.6310,0.0597,3.2316),比较符合事实.而44 mm 的等效焦距,是普通数码相机和摄像机常见范围内的数值.照片中人脸也没有明显的近距离形变.如图14 所示,较强的空间光照的一致性以及等效焦距、空间位置以及重投影图像的合理性,表明这张图片很大程度上是一张真实图片.

图14 对图1 中日本人质的分析示意图Fig.14 The analysis of the Japanese captivesphoto in Fig.1

4.4 实验结果分析

将以上案例的相关参数列表及判断意见列为表1.其中,意见1 是传统光照估计方法根据投影光照lp进行光照一致性判断给出的意见,意见2 是本文空间光照估计方法根据空间光照ls进行光照一致性判断给出的意见,意见3 是综合空间信息进行照片空间合理性分析给出的意见.结合对案例的分析,传统的光照估计方法只能得到投影光照lp,基于此进行的光照一致性分析具有明显的局限性:对因透视投影造成的照片投影光照不一致现象无法进行正确判断,对闪光灯造成的照片投影光照一致则认为光照一致.而基于透视投影下统一坐标系后的空间光照进行光照一致性分析则更符合物理事实.与此同时,结合透视投影下得到的其他空间信息,可以对照片的空间合理性进行分析,比单纯依靠光照一致性检测人脸图像篡改更有说服力.对相机参数未知的空间光照估计来说,图像中两个人脸同相机光心连线之间的夹角越大,投影光照差别越大,如果是真实图像,越容易通过优化方法得到另各种空间信息都较为合理的相机参数;如果两个人脸距离太小使得投影光照差别过小,就无法通过优化得到合理的相关参数.如果照片是篡改图像或者不满足平行光源假设的闪光灯照片,那么总会有一些参数不符合物理事实,从而给出更有说服力的判断意见.

5 结论

本文提出了一种透视投影下物体空间光照估计算法以及照片空间合理性分析方法.针对以往光照估计基于平行投影的假设、得到光照都是照片投影光照的不足,该算法将各物体坐标系统一到相机坐标系下,得到各物体相对于相机坐标系的空间光照,从物理原理上使得光照估计方法的准确度得到了显著提高.同时,根据空间光照一致性约束可以优化得到相机参数,并得到该参数下的等效焦距、人脸空间位置以及重新透视投影的图像和原图像的形变差异等信息.本文将空间光照的一致性和上述信息的合理性作为评判标准,实验结果表明,相比于传统光照估计方法仅依据照片投影光照一致性对人脸图像进行拼接篡改检测,本文提出的空间光照一致性分析方法具有更高的准确度,结合相关空间信息进行照片空间合理性分析则更有说服力.

表1 实验中各案例相关参数列表及判断意见Table 1 Comparisons of relevant parameters and corresponding judgment opinions of each case in the experiment

在图像取证和图像篡改检测领域,单纯依靠一种方法很难给出有效的意见,往往需要综合考虑各种线索才能做出判断.同时,已有的取证算法也容易被反取证算法攻击.因此,在完善提高已有算法的同时,也需要不断提出新的取证算法.而利用深度学习方法对图像内容进行取证,同样是一个值得探索和研究的方向.