基于光谱距离聚类的高光谱图像解混算法

刘颖 梁楠楠 李大湘 杨凡超

摘 要：為了解决实际高光谱解混（HU）中噪声对解混精度的影响和光谱、空间信息利用不足的问题，提出了一种改进的基于光谱距离聚类的群稀疏非负矩阵分解的解混算法。首先，引入了基于最小误差的高光谱信号辨识算法（Hysime），通过计算特征值的方式估计信号矩阵和噪声矩阵;然后，提出了一种简单的基于光谱距离的聚类算法，对多个波段生成的光谱反射率距离值小于某一值的相邻像元进行合并聚类生成空间群结构;最后，在生成的群结构基础上进行稀疏化非负矩阵分解。实验分析表明，对于模拟数据和实际数据而言，该算法都比传统算法产生更小的均方根误差（RMSE）和光谱角距离（SAD），能够产生优于同类算法的解混效果。

关键词：高光谱解混;基于最小误差的高光谱信号辨识算法;光谱距离度量;非负矩阵分解;遥感

中图分类号：TP751

文献标志码：A

Hyperspectral image unmixing algorithm based on spectral distance clustering

LIU Ying1，2， LIANG Nannan1*， LI Daxiang1，2， YANG Fanchao3

1.College of Communication and Information Engineering， Xian University of Posts and Telecommunications， Xian Shaanxi 710121， China;

2.Key Laboratory of Electronic Information  and Application Technology for Scene Investigation， Ministry of Public Security （Xian University of Posts & Telecommunications）， Xian Shaanxi 710121， China;

3.Key Laboratory of Spectral Imaging Technique， Xian Institute of Optics and Precision Mechanics， Chinese Academy of Sciences， Xian Shaanxi 710119， China

Abstract：

In order to solve the problem of the effect of noise on the unmixing precision and the insufficient utilization of spectral and spatial information in the actual Hyperspectral Unmixing （HU）， an improved unmixing algorithm based on spectral distance clustering for group sparse nonnegative matrix factorization was proposed. Firstly， the HYperspectral Signal Identification by Minimum Error （Hysime） algorithm for the large amount of noise existing in the actual hyperspectral image was introduced， and the signal matrix and the noise matrix were estimated by calculating the eigenvalues. Then， a simple clustering algorithm based on spectral distance was proposed and used to merge and cluster the adjacent pixels generated by multiple bands， whose spectral reflectance distances are less than a certain value， to generate the spatial group structure. Finally， sparse non-negative matrix factorization was performed on the basis of the generated group structure. Experimental analysis shows that for both simulated data and actual data， the algorithm produces smaller Root-Mean-Square Error （RMSE） and Spectral Angle Distance （SAD） than traditional algorithms， and can produce better unmixing effect than other advanced algorithms.

Key words：

Hyperspectral Unmixing （HU）; Hyperspectral signal identification algorithm by minimum error （Hysime）; spectral distance metric; Non-negative Matrix Factorization （NMF）; remote sensing

0 引言

高光谱遥感是将成像技术和光谱技术相结合的多维信息获取技术，同时探测目标的二维集合空间与一维光谱信息，获取高光谱分辨率的连续、多波段图像数据[1]。高光谱的遥感数据是一个光谱图像立方体，其最主要的特点是将图像空间维与光谱维信息合为一体，在获取地表空间图像的同时，会得到每个像元对应的地物光谱信息，与单波段相比，多出了一维光谱信息[1]。获得的图像空间可以直观表达每个像元在图像中的空间位置以及它周围邻域像元之间的相互关系，为高光谱图像处理提供空间信息，而光谱信息反映了地物在多个波段上的辐射光谱信息，为高光谱图像的盲源解混提供基础依据。 高光谱遥感技术已被广泛应用到城市绿化、精细农业、火山地质调查、军事目标识别、环境监测、灾害评估等行业中，因此，提升高光谱图像的解混精度对于定性定量地分析地物、进行高效目标检测有重要的意义[2]。

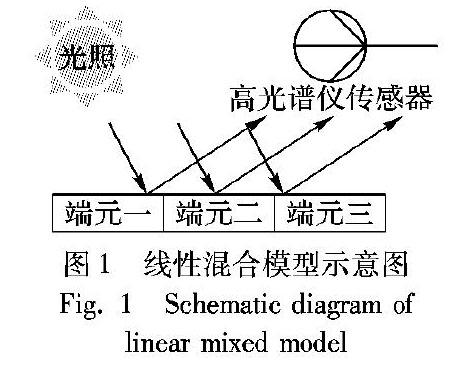
高光譜解混（Hyperspectral Unmixing，HU）即是从高光谱图像中分离出纯净像元（端元）和其相对应的分数丰度。由于高光谱数据中包含丰富的光谱和空间信息，对于高光谱解混中的盲源分离（Blind Source Separation，BSS）问题，空间稀疏正则化的非负矩阵分解（Nonnegative Matrix Factorization，NMF）成为了近几年的研究热点。由于实际地物分布的复杂性和光谱空间分辨率的不足，使得高光谱图像中存在大量的混合像元，根据是否考虑光子在不同物质之间的多重衍射[3]，将混合像元分为线性和非线性两种混合模型，线性模型不考虑地物间的相互影响，认为混合像元是纯净端元和其丰度的线性混合，如图1所示。线性混合模型结构简单、意义明确，是非线性混合模型的基础，具有更广泛的意义，因此本文的算法建立在线性混合模型的基础上进行实验。因为混合模型的存在，单纯的分类算法不能对高光谱图像进行有效、准确的检测与识别，高光谱解混算法不仅能定性分析高光谱图像中存在的端元种类，而且能表征这些种类存在的比例，使遥感图像的地物识别更加准确，并且为人们提供更多的便利。

近年来，建立在线性混合模型上的高光谱解混技术获得长足的发展，主要可以分成三类：第一类为基于几何形状的解混技术，思想是利用图像数据的空间特性获取单形体的顶点来获取端元。王天成等[4]提出的自适应鲁棒最小体积高光谱解混算法（Robust Minimum Volume based algorithm with automatically estimating regularization parameters for Hyperspectral Unmixing， RMVHU）在满足最小体积的条件下，通过引入负数惩罚正则项来代替非负性约束去增强算法对异常值、噪声值的鲁棒性，同时减小在非凸问题中陷入局部极小的概率。第二类为非监督的解混技术，用来解决盲源分离问题。聂明钰[5]提出了模糊C均值解混（Fuzzy C-Means Unmixing， FCMU）和分块的顶点成分分析（Vertex Component Analysis， VCA）的非负矩阵分解解混算法，并在实际数据集上获得了有效验证。袁博[6]提出的空间与谱间相关性分析的NMF高光谱解混算法（NMF hyperspectral unmixing algorithm based on Spatial and Spectral Correlation， NMFSSC）在NMF目标函数内、外部分别加入基于信号预测度技术的相邻波段谱间相关约束和基于马尔可夫随机场（Markov Random Field，MRF）的相邻像元空间相关约束来体现空间、谱间特征，在提高解混精度的同时减少对先验知识的依赖性。贾志成等[7]提出的基于去噪降维和蝙蝠优化的高光谱图像盲解混算法（Bat Algorithm-abundance Constrained Blind Source Separation， BA-CBSS）用蝙蝠优化算法解决陷入局部极值的问题和基于奇异值分解去噪的正交子空间投影的降维方法去增强算法抗噪声干扰能力，并获得了较好的解混结果。彭倩[2]比较了空间预处理（Spatial PreProcessing， SPP）和空间光谱预处理（Spatial Spectral PreProcessing， SSPP）两种预处理方法并提出对丰度稀疏约束和对端元平滑约束的稀疏平滑非负矩阵分解（Sparse Piecewise Smoothness constrained NMF， SPSNMF）解混算法。第三类是稀疏回归的解混技术，尹凤[8]同时考虑稀疏性和空间纹理信息，提出了一种变量裂分增强拉格朗日与总变差稀疏解混算法（Sparse Unmixing via variable Splitting Augmented Lagrangian and Total Variation， SUnSAL-TV），产生了较小的信号重构误差（Signal Reconstruction Error， SRE），能够更准确地对矿物进行识别。总的来说，近几年关于NMF的改进算法，主要集中在三方面：1）解决NMF非凸问题，如文献[5，7，9];2）增加空间与光谱约束来减少对先验知识的依赖，如文献[6，10];3）去噪降维预处理及子空间辨识，如文献[2，7，11-13]。本文的研究建立在稀疏[14]正则的非负矩阵分解的研究之上，通过加入非负可逆矩阵的方式解决非联合凸的优化问题，同时加入去噪降维预处理和光谱、空间信息约束来提高解混精度、加速算法收敛。

1 相关知识

为了解决高光谱图像解混的BSS问题，首先将解混问题转换成数学模型，然后将建立的线性数学模型转化成带约束的矩阵分解的优化问题，来模拟高光谱图像解混中已知高光谱图像数据求解端元和丰度的过程。同时，利用高光谱群结构的稀疏性来避免在迭代过程中矩阵的重复传递，从而节省空间、提高运算速度。

1.1 线性解混模型

已知高光谱图像数据X=[x1，x2，…，xN]∈RL*N，其中L表示波段数，N表示像素数，R表示实数集，第j个混合像素可表示为Xj=[x1j，x2j，…，xLj]T∈RL，根据线性解混模型，可数学表示为：

Xj=∑qi=1sijai+εj=Asj+εj（1）

其中，A为q个端元光谱反射率组成的矩阵，A可表示为A=[a1，a2，…，aq]∈RL*q，ai表示第i个光谱在L个波段上的反射率向量，Sj=[s1i，s2j，…，sMj]T∈Rq为Xj的丰度向量，sij表示第i个光谱第j个像素的丰度值，εj∈RL为加性噪声项。根据能量守恒原则，分数丰度需要满足和唯一和非负性的约束，分别可表示为sij≥0和∑qi=1sij=1[15]。

在高光谱解混中，像素间共享相同的端元矩阵A，光谱数据X可由端元矩阵A和由j个混合像素组成的丰度矩阵S相乘，再添加噪声项N表示，可向量表示为：

X=AS+N（2）

1.2 非负矩阵分解

非负矩阵分解是一种多变量分析和盲源分离的方法，1999年由Lee和Seung在Nature杂志上正式提出，在海量的盲处理数据上有优越的性能，可以适应于缺乏先验知识的高光谱图像解混[16]。对于已知的矩阵Y，可以构建模型Y∈RL*N为矩阵V∈RL*N和矩阵H∈RM*N的乘积，矩阵U为补偿项。

Y≈VH+U（3）

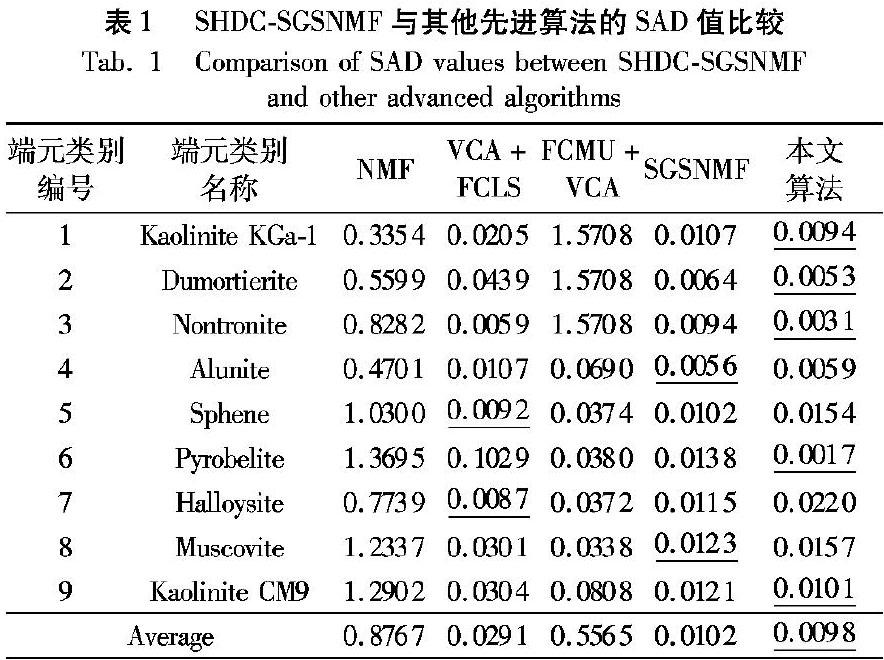
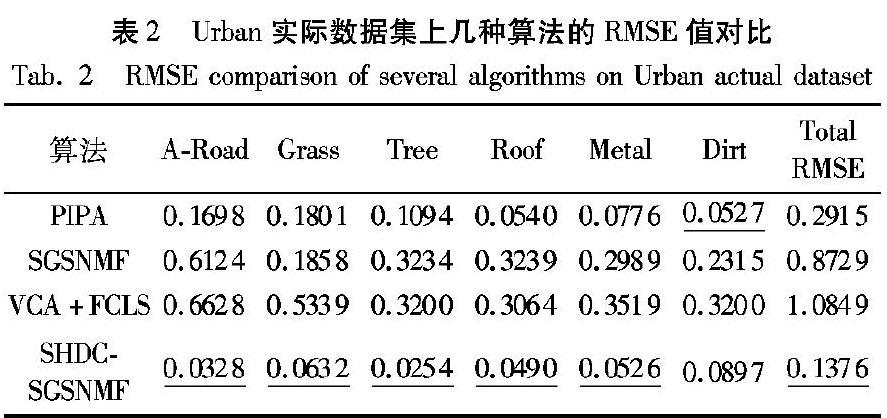
其中：U不要求非负，矩阵V和H的维度要求小于Y的维度，即M

minV，H  f（V，H）=‖Y-VH‖F

s.t. V≥0，H≥0（4）

其中：‖·‖F定義为‖Y‖F=（∑ijyij2）1/2，i、 j分别表示矩阵的行和列。

为了解决此优化问题，文献[9]提出了交替的非负最小二乘法，优化问题被分解为两个如下的迭代子问题：

Vk+1 ←arg minV≥0‖Y-VkHk‖F=max（0，Vk-ωkfV（Vk，Hk））（5）

Hk+1 ←arg minH≥0‖Y-Vk+1Hk‖F=max（0，Hk-αkfH（Vk+1，Hk））（6）

其中：k表示迭代次数，正参数ωk和αk为更新步长，用函数max（0，x）求解可直接满足非负约束，子迭代的梯度计算如下：

fV（Vk，Hk）=（VkHk-Y）（Hk）T（7）

fH（Vk+1，Hk）=（Vk+1）T（VK+1Hk-Y）（8）

值得注意得是，该优化问题对于矩阵V和H是分别凸的，但一般而言不是联合凸的，通过增加1个额外的约束，来确保解混丰度的唯一性，D为非负可逆矩阵，使：

VH≈（VD）（D-1H）（9）

1.3 空间群稀疏非负矩阵分解算法

文献[15]在实验验证了不同大小的规则网格子窗口对高光谱数据的分割处理效果的基础上，提出了一种简单的线性迭代聚类（Simple Linear Iterative Clustering， SLIC）算法，文献[16]将这种算法应用于高光谱解混中进行群结构的生成。六边形因为具有以下两个优势而被用于高光谱图像分割处理：一是六边形具有比正方形更多的非对角邻域，可以表征更多的空间信息;二是可以提供更少的边界像素距离失真。高光谱图像经SLIC分割得到p个空间群结构{1，2，…，p}。通过在空间群结构的意义上给丰度矩阵加入正则化项进行稀疏，即：

minA≥0，Sr≥0    f（A，Sr）=12∑Pp=1‖Xp-ASp‖2F+

λ∑Pp=1∑sj∈pcj‖Wpsj‖2（10）

其中：Sr表示群结构更新后的丰度矩阵，A为q个端元光谱反射率组成的矩阵，Xp表示群结构p的高光谱数据，Sp表示群结构p的丰度矩阵。λ为固定参数;cj为权衡原像素属于超像素的置信参数，用来加权局部相似性。Wp为M维的对角矩阵，用来大概控制p中的非零丰度项。

在群结构方式下实现丰度矩阵Sp和端元矩阵A的更新，公式如下：

SP ← arg minSP≥0  f（A，SP）=12‖XP-ASP‖2F+

λ∑sj∈pcj‖WPsj‖2（11）

A ←arg minA≥0  f（A，Sr）=12‖Xr-ASr‖2F（12）

其中WP的迭代公式如下：

p ← arg minSp12‖p-Ap‖2F

s.t. p≥0， 1Tp=1（13）

wpi=1p[i]+ε（14）

其中：p表示平均丰度向量;ε用来平衡无效项，避免陷入无穷大，其值应小于p。

对于模拟数据集而言，本文通过加入20dB的加性噪声去模拟真实数据的情况，然后根据SLIC[12-13]生成空间群结构，接着用VCA、完全约束最小二乘（Fully Constrained Least Squares， FCLS）分别进行端元和丰度的初始化，初始化操作一定程度上加速了算法的收敛。空间群稀疏非负矩阵分解（Spatial Group Sparsity regularized NMF， SGSNMF）算法，具体算法步骤如下：

算法1 SGSNMF。

输入：SLIC生成的P个空间群结构Xr、VCA结合FCLS生成的端元矩阵A和丰度矩阵Sr;

输出：端元矩阵A、丰度矩阵S。

程序前

终止条件1：最大迭代次数

终止条件2：限制时间

终止条件3：迭代间隔

1）根据式（14）更新Wp;

2）根据式（11）更新SP，要求满足和为一和非负性约束;

3）根据式（12）更新A。

程序后

2 本文方法

利用高光谱图像的光谱、空间信息，提出了一种简单的基于光谱距离的聚类（Simple Hyperspectral Distance Clustering， SHDC）算法来生成空间群结构，结合SGSNMF算法进行高光谱图像解混，算法流程如图2所示。

2.1 Hysime算法

Hysime算法是在2008年由Bioucas-Dias和Nascimento提出的，其基本思想是通过下述公式计算观测数据Y=[y1，y2，…，yn]∈RL*n的特征值估计噪声矩阵RN和信号矩阵RX：

RY=YYT/n（15）

RN=1n∑ni=1WiWTi（16）

RX=1n∑ni=1（yi-Wi）（yi-Wi）T（17）

其中，RY为观测数据Y的变换形式，n为Y向量的列数，Wi=Zi-Ziβi，Zi为Yi的转置矩阵，Zi为去掉Zi项后剩余项组成的顺序矩阵。然后计算RX的特征值和特征向量对，特征向量对可数学表示为（λi，ei）（i=1，2，…，L），按最小均方误差原理可得P个特征值子集，可向量表示为Σ=diag（λ1，λ2，…，λp），对应的P个相互正交的ei组成的E=[e1，e2，…，ep]即为信号子空间[8]。

2.2 简单的光谱距离聚类算法

文献[15，17]利用SLIC算法将高光谱图像分割成一定数量的六边形网格，由于没有考虑地物的空间分布情况，在光谱数据较大的情况下，对分割的每一个块进行群稀疏操作会增加计算量。本文运用光谱距离信息进行空间聚类[18]，通过计算相邻块的光谱距离对低于某一值的块进行合并，有效减少群结构的数量，从而加快算法收敛。光谱距离dx的计算公式如下：

dx=cos-1XTjXi‖Xj‖2‖Xi‖2（18）

其中：Xi、Xj表示第i、 j个像素处的光谱向量。SHDC具体算法如下。

算法2 SHDC。

输入：SLIC生成的P个空间群结构Xr、标签文件labels、逻辑相邻Am;

输出：Labels、P、C。

程序前

预处理：遍历每个像素

判断光谱标签逻辑相邻，若相邻则根据式（18）计算光谱距离矩阵D;

算法核心：if d小于某一值

更新当前标签，并保存标签;

遍历每个像素，更改当前标签

更新其他区域标签;

更新群结构C和群结构个数P;

程序后

本文将从时间复杂度和空间复杂度两方面分析算法性能。本文算法SHDC和SLIC的运行时间分别为8.848370s 和7.774267s，P的个数分别为208、173。虽然本文算法SHDC比SLIC运行时长多了约1s，但生成了更少的群结构，为后续的群稀疏非负矩阵分解节省了运行时间和存储空间。

3 实验结果

在这一部分，将对本文改进的算法与其他先进的算法在常见数据集上进行测试。为了比较解混性能，首先介绍两个指标，均方根误差RMSEm和光谱角距离SADm，计算公式如下：

RMSEm=1N ‖Sm-S·m‖F（19）

SADm=cos-1a·Tmam‖am·‖2‖am‖2（20）

其中：N为端元个数，m表示某一端元，Sm和S·m分别表示实验所得丰度和实际丰度矩阵，am和a·m分别表示实验所得端元和实际地物光谱矩阵。

3.1 模拟数据实验

本文所用的第一个数据集为模拟数据集Simu-1，包含原始端元集和丰度矩阵，其原始端元集、丰度矩生成方式参考文献[19-20]，数据大小为100×100像素，波段数量为221，从USGS光谱库中选择的9种端元，分别为Kaolinite KGa-1、Dumortierite、Nontronite、Alunite、Sphene、Pyrobelite、Halloysite、Muscovite、Kaolinite CM9，其类别与光谱曲线如图3所示。

通过本文算法、VCA+FCLS先进算法的9类端元丰度重构结果如图4～6所示，由图4可知，本文算法和VCA+FCLS算法生成的9类端元的丰度结果相近。由图5可知，在反射率的取值接近1時，本文算法生成的端元更接近实际地物事实，由图6（a）、（b）可知本文算法有更少的异常点，因此整体重构误差较小。下面将用质量评价指标均方根误差（Root-Mean-Squard Error， RMSE）和光谱角距离（Spectral Angle Distance， SAD）值，并与其他先进的算法进行比较来评估本文算法的性能。比较结果如图7和表1所示，图7中用1～9分别代表Kaolinite KGa-1、Dumortierite、Nontronite、Alunite、Sphene、Pyrobelite、Halloysite、Muscovite以及Kaolinite CM9共9类端元。

由图7可知，SGSNMF、VCA+FCLS和本文算法在RMSE上都明显优于NMF、FCMU+块VCA算法，其中本文算法对9类端元的解混性能都略微优于SGSNMF算法和其他先进算法，而SGSNMF和VCA+FCLS在多数端元上的RMSE值不相上下。SGSNMF、FCMU+块VCA 、VCA+FCLS、NMF以及本文算法的平均RMSE值分别为0.1370、1.1694、0.1944、0.7334和0.0950，本文算法获得了最小的平均RMSE值，且是唯一一个平均RMSE值达到0.1以下的算法。Simu-1模拟数据集的SAD值如表1所示，由表1可知：SGSNMF、VCA+FCLS分别在Alunite、Muscovite和Sphene、Halloysite

端元上取得最好的解混效果;而本文算法获得了最低的平均SAD值，对Kaolinite KGa-1、Dumortierite、Nontronite、Sphene 、Kaolinite CM9的端元解混精度更高，对其他四类的解混也接近算法最优水平。因此可得，本文算法在模拟数据集上对大多数类别有优越的性能。

3.2 实际数据实验

第二个数据集为常用Urban实际数据集，包含6类端元，分别为A-Road、Grass、Tree、Roof、Metal、Dirt，数据大小为256×256像素，共162个波段。实验将用上文得出的实验结果较好的三种算法以及文献[21]所述的PIPA（Proximal Interior Point Algorithm）解混算法在实际数据集上进行测试。

图8（a）、（b）为本文算法和PIPA算法的解混效果。下面用SAD、RMSE进行比较，SAD的结果如图9所示，RMSE的结果如表2所示。由图9、表2可知，本文的算法对A- Road、Grass、Tree、Roof和Metal等5类端元解混后，SAD、RMSE值都低于其他先进算法，只在Dirt端元上略高于PIPA算法，且本文算法的整体SAD值、整体RMSE值都低于VCA+FCLS、SGSNMF等其他先进算法。因此可以得出，在实际数据集上，本文算法在大多数类别上也有较优越的性能。

3.3 运行时间、迭代次数对比

本文的实验是在Window7系统Intel Core i7 Duo CPU T6600 @4.5GHz安装的Matlab 2015a版本上进行的实验。本文的实验结果均为运行10次的平均结果，运行时间和算法迭代次数对比如表3所示。

由表3运行时间和迭代次数的对比可知，本文提出的SHDC-SGSNMF算法能在提高精度的前提下更快地收敛。

4 结语

本文提出了基于光谱距离聚类的群稀疏非负矩阵分解的线性高光谱图像解混算法。首先，通过计算高光谱图像特征值来去除实际高光谱图像中的噪声;然后，利用光谱反射率的相似性生成空间群结构;最后，在群结构模型上进行稀疏化的非负矩阵分解获得端元和其相应的分数丰度。为验证本文算法的高效性，分别在模拟数据集Simu-1和实际数据集Urban

上对算法的RMSE和SAD与其他先进算法VCA+FCLS、PIPA、FCMU+块VCA、NMF和SGSNMF进行了对比，在大多数类别上都可获得较低的RMSE和SAD，因此，本文提出的算法可实现高效的高光谱图像解混。

本文虽然提升了解混精度，但与大多数算法相同，建立在已知端元个数的先验依赖下。

参考文献

[1]FENG R Y， TIAN T， LI X， et al. Rolling guidance based scaled-aware spatial sparse unmixing for hyperspectral remote sensing imagery [C]// Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium. Piscataway，NJ： IEEE， 2018： 4273-4276.

[2]彭倩.基于非負矩阵分解的高光谱图像解混研究[D].北京：中国科学院大学（中国科学院遥感与数字地球研究所），2017：1-10.（PENG Q.Hyperspectral unmixing based on constrained nonnegative matrix factorization [D]. Beijing： University of Chinese Academy of Sciences （Institute of Remote Sensing and Digital Earth， Chinese Academy of Sciences）， 2017： 1-10.）

[3]HEYLEN R， BURAZEROVIC D， SCHEUNDERS P. Non-linear spectral unmixing by geodesic simplex volume maximization [J]. IEEE Journal of Selected Topics in Signal Processing， 2011， 5（3）： 534-542.

[4]王天成，刘相振，董泽政，等.一种自适应鲁棒最小体积高光谱解混算法[J].自动化学报，2017，43（12）：2141-2159.（WANG T C， LIU X Y， DONG Z Z， et al. A robust minimum volume based algorithm with automatically estimating regularization parameters for hyperspectral unmixing [J]. Acta Automatica Sinica， 2017， 43（12）： 2141-2159.）

[5]聂明钰.高光谱图像线性解混算法研究[D].济南：山东大学，2016. （NIE M Y. Research on hyperspectral image linear unmixing algorithm [D]. Jinan： Shandong University， 2016.）

[6]袁博.空间与谱间相关性分析的NMF高光谱解混[J].遥感学报，2018，22（2）：265-276.（YUAN B. NMF hyperspectral unmixing algorithm combined with spatial and spectral correlation analysis [J] . Journal of Remote Sensing， 2018， 22（2）： 265-276.）

[7]贾志成，薛允艳，陈雷，等.基于去噪降维和蝙蝠优化的高光谱图像盲解混算法[J].光子学报，2016，45（5）：106-115.（JIA Z C， XUE Y Y， CHEN L， et al. Blind separation algorithm for hyperspectral image based on the denoising reduction and the bat optimization [J]. Acta Photonica Sinica， 2016， 45（5）：112-115.）

[8]尹凤.高光谱线性解混的理论与方法及应用研究[D].成都：成都理工大学，2017：20-28.（YIN F. Study on the theory and method of linear hyperspectral unmixing and its application[D]. Chengdu： Chengdu University of Technology， 2017： 20-28.）

[9]孔繁鏘，卞陈鼎，李云松等.非凸稀疏低秩约束的高光谱解混方法[J].西安电子科技大学学报（自然科学版），2016，43（6）：116-121.（KONG F Q， BIAN C D， LI Y S， et al. Hyperspectral unmixing method based on the non-cinvex sparse and low-rank constraints [J]. Journal of Xidian University （Natural Science）， 2016， 43（6）： 116-121.）

[10]郭文骏.基于联合稀疏表示的高光谱图像解混方法研究[D].南京：南京航空航天大学，2016：1-22.（GUO W J. Research on hyperspectral imagery unmixing algorithms based on simultaneous sparse represent [D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2016： 1-22.）

[11]陈洁，杜磊，李京，等.基于噪声白化的高光谱数据子空间维数算法[J].国土资源遥感，2017，29（2）：60-66.（CHEN J， DU L， LI J， et al. Hyperspectral data subspace dimension algorithm based on noise whitening [J]. Remote Sensing for Land and Resources， 2017， 29（2）： 60-66.）

[12]郑思远.面向异常检测的高光谱数据线性子空间估计[D].长沙：国防科学技术大学，2013：32-36.（ZHENG S Y. Hyperspectral linear subspace estimation for anomaly detection [D]. Changsha： National University of Defense Technology， 2013： 32-36.）

[13]SUN Y L， BIOUCAS-DIAS J M， ZHANG X， et al. A new classification-oriented endmember extraction and sparse unmixing approach for hyperspectral data [C]// Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium. Piscataway， NJ： IEEE， 2017： 3644-3647.

[14]ZHANG S， LI J， PLAZA J， et al. Spatial weighted sparse regression for hyperspectral image unmixing [C]// Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium. Piscataway， NJ： IEEE， 2017： 225-228.

[15]WANG X， ZHONG Y， ZHANG L， et al. Spatial group sparsity regularized nonnegative matrix factorization for hyperspectral unmixing [J]. IEEE Transactions on Geoscience and Remote Sensing， 2017， 55（11）： 6287-6304.

[16]ERTRK A， ERTRK S， PLAZA A. Unmixing with SLIC superpixels for hyperspectral change detection [C]// Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium. Piscataway， NJ： IEEE， 2016： 3370-3373.

[17]LIN C. Projected gradient methods for nonnegative matrix factorization [J]. Neural Computation， 2007， 19（10）： 2756-2779.

[18]SHEN X， BAO W， QU K W. Clustering based spatial spectral preprocessing for hyperspectral unmxing [C]// Proceedings of the 4th International Conference on Communication and Information Processing. New York： ACM， 2018： 313-316.

[19]HENDRIX E M T， GARCIA I， PLAZA J， et al. New minimum-volume enclosing algorithm for endmember identification and abundance estimation in hyperspectral data [J]. IEEE Transactions on Geoscience and Remote Sensing， 2012， 50（7）： 2744-2757.

[20]HARTIGAN J A， WONG M A. Algorithm AS 136： a K-means clustering algorithm [J]. Journal of the Royal Statistical Society. Series C （Applied Statistics）， 1979， 28（1）： 100-108.

[21]CORBINEAU M， CHOUZENOUX E， PESQUET J. PIPA： a new proximal interior point algorithm for large-scale convex optimization [C]// Proceedings of the 2018 International Conference on Acoustics， Speech and Signal processing. Piscataway， NJ： IEEE， 2018： 1343-1347.

This work is partially supported by the National Natural Science Foundation of China （61571361）， the Shaanxi International Cooperation and Exchange Project of China （2017KW-013）， the Graduate Innovation Fund for Xian University of Posts and Telecommunications （CXJJLY2018024）.

LIU Ying， born in 1972， Ph. D.， senior engineer. Her research interests include image and video retrieval.

LIANG Nannan， born in 1994， M. S. candidate. Her research interests include criminal investigation image processing， hyperspectral image processing.

LI Daxiang， born in 1974， Ph. D.， associate professor. His research interests include digital image processing， machine learning.

YANG Fanchao， born in 1987， Ph. D.， assistant research fellow. His research interests include hyperspectral imaging， polarization technique.