基于酶约束的代谢网络模型研究进展及其应用
赵欣,杨雪,毛志涛,马红武
基于酶约束的代谢网络模型研究进展及其应用
赵欣1,2,杨雪1,2,毛志涛1,2,马红武1
1 中国科学院天津工业生物技术研究所 中国科学院系统微生物技术重点实验室,天津 300308 2 中国科学院大学,北京 100049
基因组尺度代谢网络模型已经成功地应用于指导代谢工程改造,但由于传统通量平衡分析法仅考虑化学计量学和反应方向约束,模拟得到的是理论最优结果,对一些现象如代谢溢流、底物层级利用等无法准确描述。近年来人们通过在代谢网络模型中引入新的蛋白量、热力学等约束发展了新的约束优化计算方法,可以更准确真实地模拟细胞在不同条件下的代谢行为。文中主要对近年来提出的多种酶约束模型进行评述,对酶约束引入的基本思路、酶约束的数学方程表示及优化目标设定、引入酶约束后对代谢通量计算结果的影响及酶约束模型在代谢工程菌种改造中的应用等进行了全面深入的介绍,并提出了已有各种方法存在的主要问题,展望了相关方法的未来发展方向。通过引入新的约束,代谢网络模型能够更精确模拟和预测细胞在环境和基因扰动下的代谢行为,为代谢工程菌种改造提供更准确可靠的指导。
酶约束,代谢网络模型,代谢工程,酶动力学,热力学
基于化学反应计量学关系和反应可逆性约束的约束优化方法,如通量平衡分析(FBA)[1]、通量可变性分析(FVA)[2-3]等,是目前基因组尺度代谢网络模型(GEM) 分析最常用的方法[4-5]。通过这些分析方法可以计算满足特定优化目标(如最大化细胞生长速率、ATP生成或产物生成速率等)的代谢通量分布,并基于结果分析基因必需性、确定产物合成最优途径、确定代谢工程改造靶点[6]等。虽然这类方法已经比较广泛地应用在指导代谢工程改造中,但在很多情况下菌体生长时都处于一种非最优代谢状态,因此模拟结果和实际结果可能有偏差[7]。而且由FBA等方法预测细胞生长表型时需首先设定底物消耗速率才能计算最优生长速率,但实际上在实验测定底物输入速率时可同时测得生长速率,因此对于菌体生长的模拟,这类模型更适合于拟合实验结果而不是进行预测。除此之外,由于模型中仅考虑计量学和反应方向性约束,而真实细胞中的代谢流分布还受到许多其他因素影响,因此有很多生物学现象不能通过仅考虑计量学约束而不考虑其他约束的传统FBA进行准确模拟预测,举例如下。
1) 代谢溢流现象
代谢溢流是在有氧条件下,微生物处于高生长速率或高底物吸收速率时,即使氧供应充足仍有发酵副产物如乙酸、乙醇排出的现象。这种现象通常出现在单细胞生物当中[8],最常见的为酿酒酵母产乙醇和大肠杆菌生成乙酸,被统称为Crabtree effect[8-9]。此外,这种现象在某些癌细胞中也有相关报道,被称为Warburg effect[10]。尽管代谢溢流现象已经被广泛研究,但传统的代谢网络模型由于仅以生长最大化为目标,并不能准确描述这种副产物生成的现象。
2) 微生物在多种碳源上的层级利用现象
细菌在两种及以上混合碳源的培养基上培养时会表现出“先后利用” (Diauxie) 和“共利用” (Co-utilization) 的不同代谢行为[11-12]。传统代谢网络约束优化方法因需要人为设定底物消耗速率,无法解释细胞为何倾向于利用两种底物中的一种或同时利用。需要考虑新的机理整合新的约束进行模拟。
在复杂的生物体内,细胞代谢受到很多因素的调控与限制,酶浓度的限制就是其中的一种,即在细胞内催化代谢反应的酶的总量是有限的,在1 g细胞干重中总蛋白的量一般不超过60%,而催化反应的酶又只占总蛋白的一定比例。因此当存在酶活很低的酶时,细胞代谢转化的速率就会受到限速酶能达到的最高浓度限制。并且,最近的研究结果表明,代谢溢流以及底物层级利用现象的发生与微生物体内的酶浓度限制有关[13-15]。基于这一考虑,近年来科学家们开发了多种方法将细胞内酶的约束整合到代谢网络模型中,由此对与酶浓度限制相关的代谢现象进行更准确的模拟和预测。不同的方法从不同角度,如酶在细胞内的空间拥挤度、酶的催化活性、代谢反应热力学等,对细胞内的酶量约束进行数学表征,进而通过适当的约束条件或优化目标求出满足酶总量约束或者最小化酶成本的代谢通量分布及相应酶量分布。这种模型目前已经被成功地应用到指导菌种代谢工程改造当中[16]。
文中将结合笔者的部分研究结果,对各种酶约束模型的基本原理、构建方法及其在生物学研究和代谢工程领域的应用情况进行详细介绍。
1 整合动力学信息对酶浓度水平进行限制
2007年Beg等基于大分子拥挤的原理开发了FBAwMC (Flux balance analysis with molecular crowding) 的酶约束方法[17]。考虑到细胞的总体积是有限的,在有限的细胞质体积内大分子(催化各种反应的酶) 的浓度受到物理和空间上的一个限制[18-20],即在细胞质中酶的摩尔体积(v) 与摩尔数(n)满足
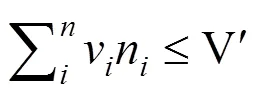

引入一个拥挤系数i,其中

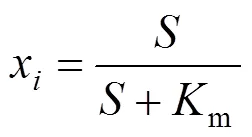
对于每一个酶都可以根据底物浓度、m值、cat值、酶的分子量、酶的质量体积和细胞质密度这6个参数求解出拥挤系数a,它反映了第个酶对总体积拥挤程度的贡献。但是由于底物浓度和m值等实验数据量有限,因此FBAwMC方法在进行模拟计算时通过使实验测量值与模拟值之间的方差最小,选取了一个统一的拥挤系数值=(0.004±0.000 5) h∙g/mmol。这种在物理空间水平上对酶浓度进行限制的方法能够通过求解得到催化每个反应的酶所占的空间体积以及每一个酶的浓度信息。
在Beg等开发出第一个在酶浓度水平上对代谢网络模型进行约束的方法后,人们又基于相似思路提出了更多类似模型扩展方法。例如2011年Shlomi等为了研究人类癌细胞中Warburg effect现象产生的原因而开发的方法[23],以及其在2012年为了探究微生物的实际生长速率针对开发的MOMENT (Metabolic modeling with enzyme kinetics)算法[24],都是在FBAwMC方法的基础上进行的改良和扩展。与FBAwMC不同的是这两种方法没有在空间体积上对酶的浓度进行限制,而是直接为细胞内酶的总量施加了浓度上限,使细胞代谢时的总酶需求量不超过该设定值(,单位g/g DW)。根据反应的最大速率与催化反应的酶浓度之间的关系得到约束方程,

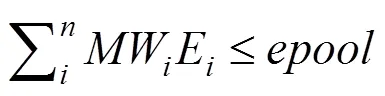
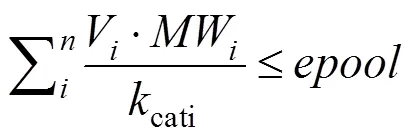
两种方法在酶约束原理上基本一致,不同的是在计算酶的总浓度时,MOMENT直接将细胞内蛋白质的质量分数ptot作为酶浓度上限 (中为0.56 g蛋白/g DW[25]),对于微生物来说这显然是一个偏高的值,因为细胞内的蛋白不仅包括催化反应的酶还包括一些结构蛋白、转运蛋白等。而在对人类癌细胞内的Warburg effect现象进行研究时,Shlomi等还基于蛋白质组学数据计算出了模型中催化代谢反应的酶占细胞内总蛋白质的质量分数为0.1 g酶/g蛋白[26],在此基础上对细胞内的总酶浓度作了进一步限制。两种方法的共同问题是假定酶均处于底物饱和状态,但实际细胞内很多酶的底物浓度都未达到饱和浓度,因此这些方法计算得到的酶浓度值都偏低。
2017年,Sánchez等提出GECKO[27]方法成功地构建了带有酶约束的酿酒酵母基因组尺度代谢网络模型。与上述提到的两种方法不同的是,在计算总酶量时考虑到了酶的平均饱和度σ[28-29]的影响(表1)。2019年Massaiu等利用GECKO的方法构建出了枯草杆菌的酶约束模型ec_iYO844[16],该模型中仅运用了17个中心代谢反应的cat值,严格地讲,并不是基因组尺度的酶约束模型,但运用该模型进行与中心代谢途径相关的表型预测时,相对于普通模型iYO844[30]的预测结果有了显著提高。
在上述酶约束模型构建时均需要酶的cat值来确定满足酶约束的最优酶浓度分布。目前虽然有很多数据库如BRENDA[31]、SABIO-RK[32]、Metacyc[33]等都已经收集了很多酶的相关动力学参数,但是仍有大量酶的cat数据缺失,对同一个酶不同文献报道的结果也常存在较大差异[34]。因此酶cat值的获取和可靠性是影响这类模型模拟预测结果准确性的关键。最近Palsson课题组针对cat值缺失的问题开发了一种机器学习方法,基于酶结构、通量取样信息等成功地对cat值进行预测[35],为解决这一问题提供了新的思路。
除了对FBAwMC扩展的方法之外,人们还开发了一些其他将动力学的相关信息引入GEM来增加酶约束的方法。例如2010年Yizhak等开发的IOMA算法[36]整合了代谢组学和蛋白质组学数据,通过这些测得数据对代谢网络模型中部分反应的通量进行限制,使实验测量值与预测值之间的误差平方和最小来求得代谢通量分布。它首先从经典的米氏方程出发推导出反应通量与代谢物浓度和酶浓度之间的关系,得到:

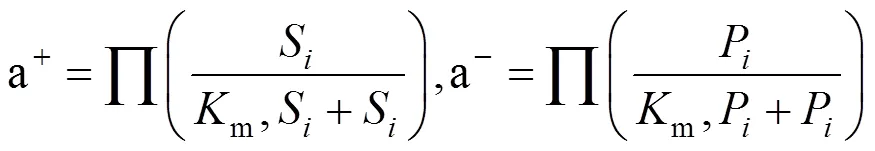
其中e表示参考状态下的酶浓度,e表示实验测量的酶浓度。使核心反应(可以得到代谢物组学和蛋白质组学数据的反应) 的模拟通量尽可能与通过公式(8) 计算出来的通量一致,引入一个可变参数,约束方程变为:
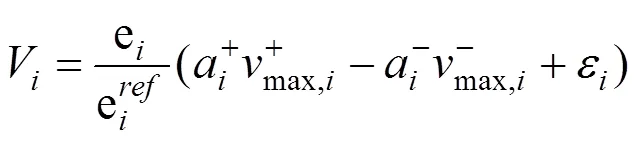
V表示模拟得到的通量,优化目标是使的误差平方和最小。

IOMA类似于MOMA[37]的思想,以通量变化最小为优化目标,可以预测在不同因素扰动下通量的改变,并且预测结果显著优于MOMA。但这种方法依赖大量的实验数据包括代谢物浓度、酶浓度和m值等,对基因组规模模型应用时会因为大量数据缺失而无法模拟。



随着生长速率的变化,另外3个部分的蛋白成本会相应调整以满足方程(12)的约束,进而引起碳源摄入的再调整。
与CAFBA原理相似,专门针对的溢流代谢研究开发的PAT (Proteome allocation theory) 方法[42]将细胞内总酶量分为发酵相关的酶、呼吸相关的酶以及用于细胞其他活动的酶这3部分,根据3部分的总和为1得出约束方程。这个方程只适合专注于对微生物的溢流代谢现象进行分析,在对其他代谢现象分析时存在一定的局限性。
2 整合动力学与热力学信息对酶浓度水平进行限制
前面提到的方法都是从动力学角度出发经过公式推导得出酶限制的方程,接下来将主要介绍结合热力学和动力学经典公式来对GEM添加酶约束的方法。
最早将热力学信息引入GEM的思想是2004年Holzhütter[43]提出的,将热力学平衡常数K作为可逆反应通量的权重因子来求出通量和最小的解。之后就出现了将热力学与动力学信息结合来对代谢反应的酶成本进行表征进而约束代谢网络模型的方法。2013年开发的mTOW (Metabolic tug-of-war)[44]能够求解出稳态时酶效率最高、总代谢物负载最小的途径。在估计酶成本时,引入了一个惩罚项,假定需要维持一定反应通量的细胞必须通过更高的酶成本来补偿较小的热力学驱动力,热力学驱动力越小酶成本就会越高。由可逆速率定律=(+––) (表示催化反应的酶浓度,+和–分别表示正向和逆向的反应速率)出发,得到酶成本的函数关系(方程14)。当反应的热力学驱动力小于下限的阈值时,酶成本无穷大;当大于一定阈值时,酶成本可以忽略不计;在阈值范围内酶成本是反应速率与代谢物浓度的函数。

代谢物浓度通过以下约束求出,其在满足经验值[45](17)约束的同时还需使反应的吉布斯自由能变化大于阈值。



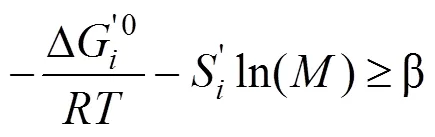
mTOW可以求解出反应的吉布斯自由能变化、代谢物浓度以及酶浓度信息,是第一个不需要利用动力学模型就可以得到代谢物浓度的方法。在求解上,得到的是代谢物浓度与酶浓度之间的一个折中,它没有考虑动力学参数对酶浓度的影响,因此不需要动力学参数的输入。虽然对酶浓度的估计是一个近似值,但模拟生长在以葡萄糖为碳源的基本盐培养基上的酶浓度时,预测结果与实验结果之间仍有比较好的相关性。
与mTOW同期,Flamholz等[46]提出的方法可以求出反应在满足热力学驱动力为正值下的最小酶成本。类似于mTOW,在求解最小酶成本时,Flamholz的方法限制了热力学驱动力必须为正值,以保证反应可以正向进行。在对酶成本进行表征时,首先从米氏方程出发结合Haldane关系推导出一个简化的适合于任意反应的速率方程。在推导时假设了酶全部与底物结合,对产物饱和度的影响忽略不计,因此计算得到的酶浓度值偏低。对这个方法进行完善和优化以后的ECM方法[47]将cat、代谢物浓度、吉布斯自由能变化、饱和度相关因素以及与调控有关的因素等作为反应通量的权重因子来对酶成本进行评估,这个方法可以自由地选择将哪些因素考虑到酶成 本的计算当中。同样的,考察的因素越多需要的实 验参数就会越多,但结果就会更加接近于真实情况。
corsoFBA[48]也是求解的FBA解空间下酶成本最小的途径,通过热力学驱动力来对酶成本进行罚分,驱动力越大酶成本越小。这种方法可以将热力学的限制整合入模型中,计算出途径的酶成本大小。但它在表征酶成本时,仅定性地考虑了分子量和热力学驱动力这两个因素的影响,因此计算结果仅能用于途径之间酶成本的评价排序,数值本身并不代表真实的酶用量。各种酶约束模型的约束方程及相关信息见表1和表2。
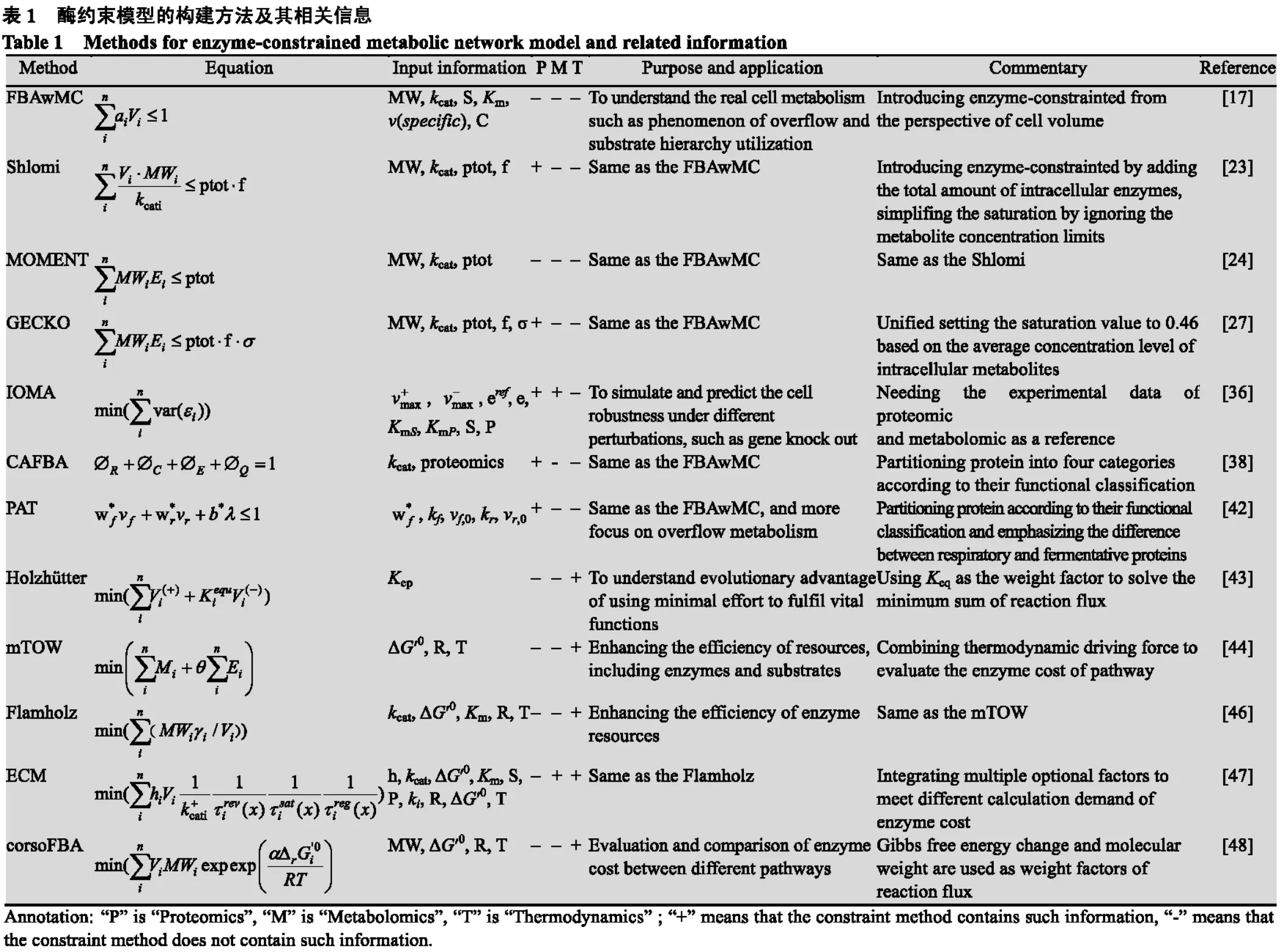

表2 缩略语与名称的对应信息
3 酶约束模型在生物表型分析和代谢工程中的应用
目前构建出来的酶约束模型能够显著提高对细胞表型的预测能力,通过模拟预测各种生物学现象揭示微生物代谢策略,在基础生物学研究和指导代谢工程改造当中得到广泛的应用。
3.1 模拟微生物在单一碳源下的生长情况
Beg等和Adadi等分别利用FBAwMC、MOMENT对在10种和24种不同单一碳源下的最大生长速率进行了预测,结果显示与实验测量值显著相关,其中MOMENT预测的最大生长速率与实验测量值的皮尔逊相关系数为0.47 (值为0.02)[17,24]。通过GECKO方法构建的的酶约束模型ecYeast7显著降低了模型中60%的反应的通量可变性,也成功预测了其在3种不同培养基、12种不同碳源下的最大生长速率,同时还与未考虑酶约束的普通基因组尺度代谢网络模型Yeast7的预测值进行比较,ecYeast7预测结果的平均相对偏差仅为8%,而Yeast7预测值的平均相对偏差高达100%。证明了酶约束模型能够在不需要人为设定底物输入速率的情况下很好地对微生物的最大生长速率进行预测[27]。
Flamholz等利用酶成本最小化的方法对EMP和ED途径间的选择进行分析,揭示了微生物生长是在能量和酶成本之间进行权衡之后选择了不同的糖酵解策略。EMP途径能量产生效率高但酶成本也高,当酶成为限制因素时就会切换到能量产生效率低但酶成本也低的ED途径[46]。
3.2 模拟并研究微生物体内的代谢溢流(Overflow) 现象
代谢溢流现象普遍存在于微生物体内(图1),针对普通基因组尺度代谢网络模型不能预测该现象的问题,Sánchez利用构建的ecYeast7模型成功模拟出在无氧和有氧条件时高生长速率和高压生长状态下体内产生的Crabtree effect[27],展示了酿酒酵母体内存在的高效率代谢途径(即经过TCA和呼吸链产能) 与低效率代谢途径(即经过糖酵解后溢出发酵产物) 间的切换。但利用普通的Yeast7模型则无法模拟出酿酒酵母体内的这种代谢溢流现象。

图1 不同菌株体内存在的代谢溢流现象
Vazquez等利用已经开发出来的FBAwMC方法也解释了细胞内酶浓度的限制是代谢溢流产生的主要原因[49],与目前对于代谢溢流现象的研究结论相统一。van Hoek还利用分子拥挤的方法探究了不同微生物采取不同溢流策略的现象(酵母在开始利用低效率的溢流代谢途径后高效率代谢途径的比例随之下降,而大肠杆菌在出现溢流时高效率途径仍维持较高的水平),发现维持氧化还原平衡在微生物途径调整策略中发挥关键作用[50]。
今年Mori等利用CAFBA的方法研究了在生长和酶成本之间进行权衡之后选择的呼吸和发酵两种代谢行为。通过将摄入的碳源通量分为生成能量的碳和生成生物质前体的碳两部分,证明了ATP合成的效率是微生物在细胞得率和酶成本之间进行权衡的关键驱动力[51]。
3.3 探究微生物的底物层级利用情况
Beg等利用FBAwMC评估了酶浓度限制对细胞代谢的作用,检测了在混合碳源限制培养基中的底物利用情况。FBAwMC模拟结果显示在混合碳源下微生物会经过首先利用葡萄糖,再同时利用半乳糖、乳酸盐和麦芽糖,最后利用甘油和乙酸这3个阶段[17],与实验观察到的结果一致。但仅考虑计量学约束而不考虑其他约束的传统FBA模拟结果表示菌体会同时利用所有的碳源,这与实验结果不相符。最近汤超研究组也利用粗粒模型对微生物在多碳源下的底物利用策略进行模拟[15],但与酶约束模型相比粗粒模型并不能给出特定蛋白的浓度。由此可见,基于酶约束的模型可更好地用来研究微生物的底物层级利用情况(图2)。
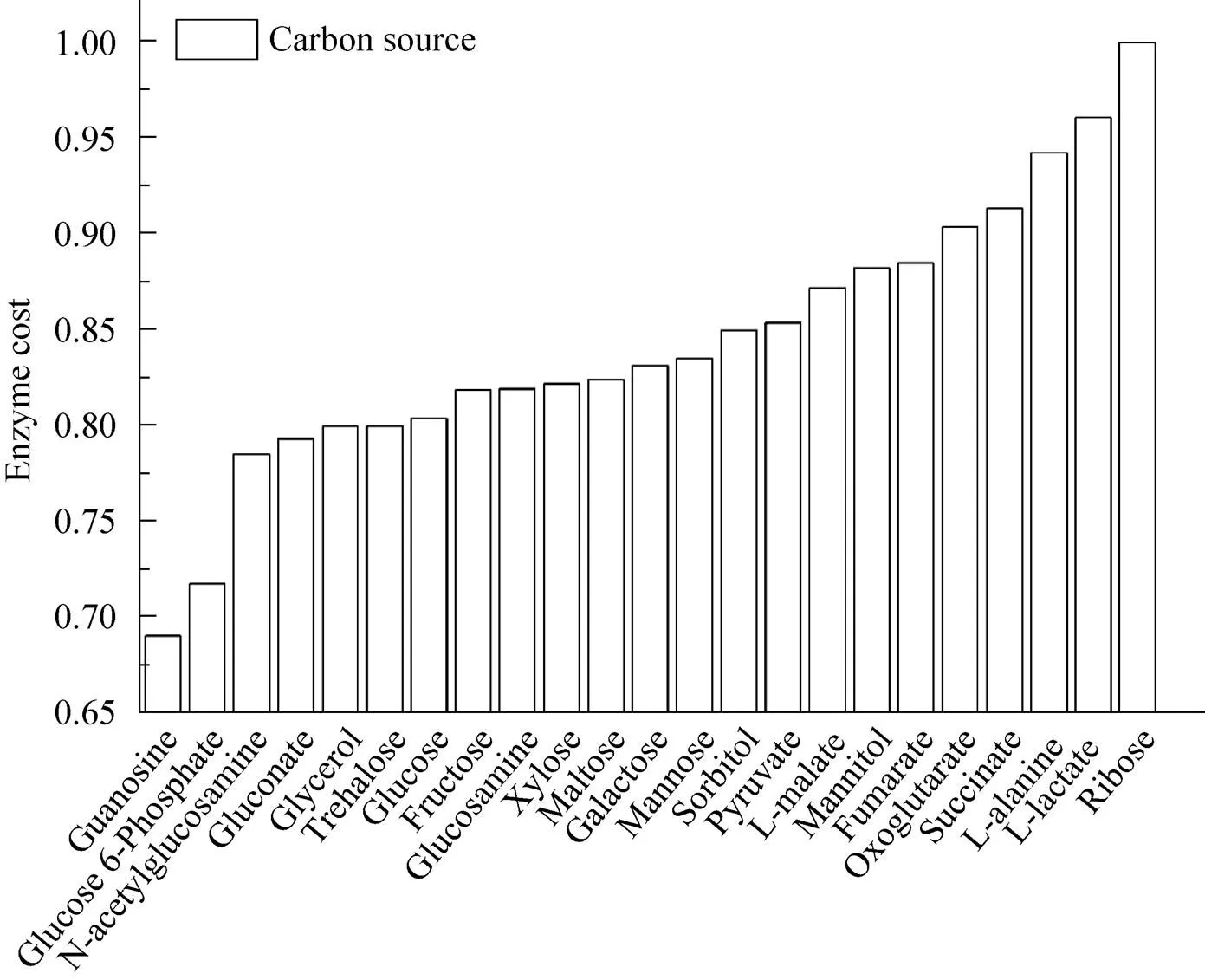
图2 E. coli在23种单一碳源下单位质量生物质合成需要的酶成本(以核糖作为碳源时的酶成本进行归一化)
3.4 酶约束模型在代谢工程中的应用
除了基础的生物学现象和机理研究以外,酶约束模型还能够成功地进行靶点预测指导代谢工程改造。Sánchez等利用ecYeast7通过通量控制分析(FCC)[52]的方法找到了酿酒酵母产富马酸的关键酶作为改造靶点[27]。
Massaiu等通过利用MOMA算法对iYO844和ec_iYO844两个模型进行单基因和双基因敲除,来预测提高多聚谷氨酸产量的靶点基因。两个模型对于单基因敲除的预测结果相一致,双基因敲除结果存在差异。后对双基因敲除靶点的预测结果进行验证,结果表明,的酶约束模型ec_iYO844预测的双基因敲除靶点的敲除能够明显提高目标产品多聚谷氨酸的产量,而按照传统的iYO844模型预测结果进行的双基因敲除却未能达到预期结果。进一步证明基于酶约束的模型在指导代谢工程改造中相较于普通模型具有更广泛的应用前景[16]。
虽然目前酶约束模型在指导代谢工程改造中的应用实例较少,但其构建原理和方法具有很好的生物学意义及可行性,可以预见这类模型具备更为精确地指导代谢工程改造的潜力。如根据催化每一步反应所需的酶量来确定限速酶,然后理性选择过表达或酶改造等实验策略来优化途径,提高目标产品得率。另外,此类模型模拟的理论上非最优但更接近于实际的途径还可用于指导途径中副产物的去除等,对于工业生产也具有重要的意义。此外酶约束模型还可以预测在环境扰动下(如高温条件),细胞内发生的代谢行为变化,进而指导过程控制和菌株优化[27]。
4 总结与展望
本文主要总结了近年来开发的各种基于酶约束的代谢网络模型构建方法,这些方法结合动力学中的米氏方程或热力学第二定律通过引入cat、m、饱和度、eq、吉布斯自由能以及代谢组学和蛋白质组学数据来对反应消耗的酶成本进行表征,进而通过适当的约束条件或优化目标求出满足酶总量约束或者最小化酶成本的代谢通量分布及相应酶量分布等信息。经研究发现,这种整合了酶约束的代谢网络模型在表型预测上显著优于普通FBA模型,能够解决目前普通基因组尺度代谢网络模型不能解释的一些生物学现象,可以提供更准确可靠的代谢工程改造指导。虽然目前这些方法还存在一些不足和可以改进的地方,但其为开发其他以酶约束为基础的新的约束方法奠定了坚实的基础。
首先,在给酶成本添加总浓度限制的方法中,考虑的是整个细胞内代谢酶的总量,这个值只适合用于对微生物的生长进行预测,当对某一产品的合成途径预测时这往往是一个过高的酶浓度值(因可用于某一特定合成途径的酶占总蛋白量更小)。对此可以通过将总酶量的限制拆分成对几个不同功能相关的酶的量限制来进一步细化,这实际上反映了细胞在基因调控水平的一种约束。
其次,在同工酶、多功能酶的处理上,目前的优化结果都是倾向于利用其中酶活最高的酶,而在真实细胞中具有不同比酶活的同工酶会在不同条件下表达,对此酶约束模型并不能很好模拟。可以考虑以酶约束模型作为基础,引入某种形式的调控约束,通过两者结合开发出能模拟细胞内同工酶和多功能酶表达策略的方法,以实现更精确的细胞行为模拟。
最后,这些不同的方法都仅仅是涉及到细胞内影响酶成本的部分因素。对相同质量的酶可能会因为氨基酸组成不同而具有不同合成成本,如何以酶约束方法为基础,再将这些氨基酸合成成本的约束因素引入到模型中开发新的方法,也是这些酶约束模型进一步完善的方向。
[1] Orth JD, Thiele I, Palsson BØ. What is flux balance analysis? Nat Biotechnol, 2010, 28(3): 245–248.
[2] Mahadevan R, Schilling CH. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab Eng, 2003, 5(4): 264–276.
[3] Gudmundsson S, Thiele I. Computationally efficient flux variability analysis. BMC Bioinformatics, 2010, 11: 489.
[4] Yuan QQ, Li FR, Luo H, et al. Discovery of new strain modification strategies by metabolic network analysis. Chem Ind Eng Prog, 2017, 36(12): 4592–4600 (in Chinese). 袁倩倩, 李斐然, 罗浩, 等. 由代谢网络分析发现菌种代谢工程改造新策略. 化工进展, 2017, 36(12): 4592–4600.
[5] Hao T, Ma HW, Zhao XM. Progress in automatic reconstruction and analysis tools of genome-scale metabolic network. Chin J Biotech, 2012, 28(6): 661−670 (in Chinese).郝彤, 马红武, 赵学明. 基因组尺度代谢网络自动重构及分析工具研究进展. 生物工程学报, 2012, 28(6): 661–670.
[6] Feng J, Gu YY, Quan YF, et al. Improved poly-γ-glutamic acid production inby modular pathway engineering. Metab Eng, 2015, 32: 106–115.
[7] Schuetz R, Kuepfer L, Sauer U. Systematic evaluation of objective functions for predicting intracellular fluxes in. Mol Syst Biol, 2007, 3: 119.
[8] Molenaar D, van Berlo R, de Ridder D, et al. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol Syst Biol, 2009, 5: 323.
[9] Varma A, Palsson BO. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-typeW3110. Appl Environ Microbiol, 1994, 60(10): 3724–3731.
[10] Hsu PP, Sabatini DM. Cancer cell metabolism: Warburg and beyond. Cell, 2008, 134(5): 703–707.
[11] Hermsen R, Okano H, You CH, et al. A growth-rate composition formula for the growth of.on co-utilized carbon substrates. Mol Syst Biol, 2015, 11(4): 801.
[12] Narang A, Pilyugin SS. Bacterial gene regulation in diauxic and non-diauxic growth. J Theor Biol, 2007, 244(2): 326–348.
[13] Basan M, Hui S, Okano H, et al. Overflow metabolism inresults from efficient proteome allocation. Nature, 2015, 528(7580): 99–104.
[14] Berkhout J, Bosdriesz E, Nikerel E, et al. How biochemical constraints of cellular growth shape evolutionary adaptations in metabolism. Genetics, 2013, 194(2): 505–512.
[15] Wang X, Xia K, Yang XJ, et al. Growth strategy of microbes on mixed carbon sources. Nat Commun, 2019, 10(1): 1279.
[16] Massaiu I, Pasotti L, Sonnenschein N, et al. Integration of enzymatic data ingenome-scale metabolic model improves phenotype predictions and enablesdesign of poly-γ-glutamic acid production strains. Microb Cell Fact, 2019, 18(1): 3.
[17] Beg QK, Vazquez A, Ernst J, et al. Intracellular crowding defines the mode and sequence of substrate uptake byand constrains its metabolic activity. Proc Natl Acad Sci USA, 2007, 104(31): 12663–12668.
[18] Minton AP. Influence of macromolecular crowding upon the stability and state of association of proteins: predictions and observations. J Pharm Sci, 2005, 94(8): 1668–1675.
[19] Hall D, Minton AP. Macromolecular crowding: qualitative and semiquantitative successes, quantitative challenges. Biochim Biophys Acta, 2003, 1649(2): 127–139.
[20] Ellis RJ. Macromolecular crowding: obvious but underappreciated. Trends Biochem Sci, 2001, 26(10): 597–604.
[21] Zimmerman SB, Trach SO. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of. J Mol Biol, 1991, 222(3): 599–620.
[22] Lee B. Calculation of volume fluctuation for globular protein models. Proc Natl Acad Sci USA, 1983, 80(2): 622–626.
[23] Shlomi T, Benyamini T, Gottlieb E, et al. Genome-scale metabolic modeling elucidates the role of proliferative adaptation in causing the Warburg effect. PLoS Comput Biol, 2011, 7(3): e1002018.
[24] Adadi R, Volkmer B, Milo R, et al. Prediction of microbial growth rate versus biomass yield by a metabolic network with kinetic parameters. PLoS Comput Biol, 2012, 8(7): e1002575.
[25] Bremer H, Dennis PP. Modulation of chemical composition and other parameters of the cell by growth rate//Neidhardt FC, Curtiss III R, Ingraham JL, et al, Eds.and Salmonella: Cellular and Molecular Biology. 2nd ed. Washington, DC: American Society for Microbiology, 1996: 1553–1569.
[26] Lee JK, Havaleshko DM, Cho H, et al. A strategy for predicting the chemosensitivity of human cancers and its application to drug discovery. Proc Natl Acad Sci USA, 2007, 104(32): 13086–13091.
[27] Sánchez BJ, Zhang C, Nilsson A, et al. Improving the phenotype predictions of a yeast genome-scale metabolic model by incorporating enzymatic constraints. Mol Syst Biol, 2017, 13(8): 935.
[28] Bakker BM, Bro C, Kötter P, et al. The mitochondrial alcohol dehydrogenase Adh3p is involved in a redox shuttle in. J Bacteriol, 2000, 182(17): 4730–4737.
[29] van Hoek P, van Dijken JP, Pronk JT. Effect of specific growth rate on fermentative capacity of baker’s yeast. Appl Environ Microbiol, 1998, 64(11): 4226–4233.
[30] Oh YK, Palsson BO, Park SM, et al. Genome-scale reconstruction of metabolic network inbased on high-throughput phenotyping and gene essentiality data. J Biol Chem, 2007, 282(39): 28791–28799.
[31] Placzek S, Schomburg I, Chang A, et al. BRENDA in 2017: new perspectives and new tools in BRENDA. Nucleic Acids Res, 2017, 45(D1): D380–D388.
[32] Wittig U, Rey M, Weidemann A, et al. SABIO-RK: an updated resource for manually curated biochemical reaction kinetics. Nucleic Acids Res, 2018, 46(D1): D656–D660.
[33] Caspi R, Billington R, Ferrer L, et al. The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases. Nucleic Acids Res, 2016, 44(D1): D471–D480.
[34] Bar-Even A, Noor E, Savir Y, et al. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry, 2011, 50(21): 4402–4410.
[35] Heckmann D, Lloyd CJ, Mih N, et al. Machine learning applied to enzyme turnover numbers reveals protein structural correlates and improves metabolic models. Nat Commun, 2018, 9(1): 5252.
[36] Yizhak K, Benyamini T, Liebermeister W, et al. Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model. Bioinformatics, 2010, 26(12): i255–i260.
[37] Segrè D, Vitkup D, Church GM. Analysis of optimality in natural and perturbed metabolic networks. Proc Natl Acad Sci USA, 2002, 99(23): 15112–15117.
[38] Mori M, Hwa T, Martin OC, et al. Constrained allocation flux balance analysis. PLoS Comput Biol, 2016, 12(6): e1004913.
[39] Scott M, Gunderson CW, Mateescu EM, et al. Interdependence of cell growth and gene expression: origins and consequences. Science, 2010, 330(6007): 1099–1102.
[40] Hui S, Silverman JM, Chen SS, et al. Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol Syst Biol, 2015, 11(2): 784.
[41] You CH, Okano H, Hui S, et al. Coordination of bacterial proteome with metabolism by cyclic AMP signalling. Nature, 2013, 500(7462): 301–306.
[42] Zeng H, Yang AD. Modelling overflow metabolism inwith flux balance analysis incorporating differential proteomic efficiencies of energy pathways. BMC Syst Biol, 2019, 13(1): 3.
[43] Holzhütter HG. The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur J Biochem, 2004, 271(14): 2905–2922.
[44] Tepper N, Noor E, Amador-Noguez D, et al. Steady-state metabolite concentrations reflect a balance between maximizing enzyme efficiency and minimizing total metabolite load. PLoS ONE, 2013, 8(9): e75370.
[45] Bennett BD, Kimball EH, Gao M, et al. Absolute metabolite concentrations and implied enzyme active site occupancy in. Nat Chem Biol, 2009, 5(8): 593–599.
[46] Flamholz A, Noor E, Bar-Even A, et al. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc Natl Acad Sci USA, 2013, 110(24): 10039–10044.
[47] Noor E, Flamholz A, Bar-Even A, et al. The protein cost of metabolic fluxes: prediction from enzymatic rate laws and cost minimization. PLoS Comput Biol, 2016, 12(11): e1005167.
[48] Schultz A, Qutub AA. Predicting internal cell fluxes at sub-optimal growth. BMC Syst Biol, 2015, 9: 18.
[49] Vazquez A, Oltvai ZN. Macromolecular crowding explains overflow metabolism in cells. Sci Rep, 2016, 6: 31007.
[50] van Hoek MJ, Merks RM. Redox balance is key to explaining full. partial switching to low-yield metabolism. BMC Syst Biol, 2012, 6: 22.
[51] Mori M, Marinari E, de Martino A. A yield-cost tradeoff governs’s decision between fermentation and respiration in carbon-limited growth. npj Syst Biol Appl, 2019, 5(1): 16.
[52] Nilsson A, Nielsen J. Metabolic trade-offs in yeast are caused by F1F0-ATP synthase. Sci Rep, 2016, 6: 22264.
Progress and application of metabolic network model based on enzyme constraints
Xin Zhao1,2, Xue Yang1,2, Zhitao Mao1,2, and Hongwu Ma1
1 Key Laboratory of Systems Microbial Biotechnology, Tianjin Institute of Industrial Biotechnology, Chinese Academy of Sciences, Tianjin 300308, China 2 University of Chinese Academy of Sciences, Beijing 100049, China
Genome-scale metabolic network models have been successfully applied to guide metabolic engineering. However, the conventional flux balance analysis only considers stoichiometry and reaction direction constraints, and the simulation results cannot accurately describe certain phenomena such as overflow metabolism and diauxie growth on two substrates. Recently, researchers proposed new constraint-based methods to simulate the cellular behavior under different conditions more precisely by introducing new constraints such as limited enzyme content and thermodynamics feasibility. Here we review several enzyme-constrained models, giving a comprehensive introduction on the biological basis and mathematical representation for the enzyme constraint, the optimization function, the impact on the calculated flux distribution and their application in identification of metabolic engineering targets. The main problems in these existing methods and the perspectives on this emerging research field are also discussed. By introducing new constraints, metabolic network models can simulate and predict cellular behavior under various environmental and genetic perturbations more accurately, and thus can provide more reliable guidance to strain engineering.
enzyme constraints, metabolic network model,metabolic engineering, enzyme kinetics, thermodynamics
10.13345/j.cjb.190220
马红武 中国科学院天津工业生物技术研究所“百人计划”研究员,中科院系统微生物技术重点实验室副主任。2001年在天津大学获得生物化工博士学位。后分别在德国和英国从事研究工作。2011年底回国任中科院天津工业生物技术研究所研究员。主要研究方向包括代谢网络分析和途径设计、代谢工程、计算生物学软件开发等,在相关领域取得了在国际上具有重要影响的研究成果,在、等刊物发表学术论文40余篇,SCI引用千余次,2014年获汤森路透高被引科学家奖。兼任中国生物工程学会生物资源专业委员会副主任委员。

赵欣, 杨雪, 毛志涛, 等. 基于酶约束的代谢网络模型研究进展及其应用. 生物工程学报, 2019, 35(10): 1914–1924.
Zhao X, Yang X, Mao ZT, et al. Progress and application of metabolic network model based on enzyme constraints. Chin J Biotech, 2019, 35(10): 1914–1924.
May 29, 2019;
July 15, 2019
Supported by: International Partnership Program of Chinese Academy of Sciences (No. 153D31KYSB20170121), National Key Research and Development Program of China (No. 2018YFA0900301).
Hongwu Ma. Tel: +86-22-24828735; E-mail: ma_hw@tib.cas.cn
中国科学院国际合作局对外合作重点项目(No. 153D31KYSB20170121),科技部重点专项(No. 2018YFA0900301) 资助。
2019-07-23
http://kns.cnki.net/kcms/detail/11.1998.Q.20190722.1442.004.html
(本文责编 郝丽芳)

