工业生物发酵过程模拟:进展与发展趋势
李德茂,陈吴西,郭蔚,李超峰
工业生物发酵过程模拟:进展与发展趋势
李德茂,陈吴西,郭蔚,李超峰
中国科学院天津工业生物技术研究所 天津市工业生物系统与过程工程重点实验室,天津 300308
工业生物发酵是工业生物技术规模化生产必需的基本操作单元。对微生物细胞及其反应器进行数学模拟将有助于加深对发酵过程的理解,也将为新的合成生物构建提供解决策略。文中对工业发酵系统的特点、数学模拟的发展历史、数学模型的分类和特点、用途等作了深入阐述,并展望了全发酵系统模拟的发展趋势。
工业生物技术,发酵,模拟与仿真,机理模型,经验模型,混合模型
工业生物技术是利用生物化学反应进行大规模的物质加工与转化的先进制造技术,它以工业发酵或工业催化为技术主体生产包括生物基化学品、生物基材料、生物燃料等产品,涉及食品、能源等许多重要的工业领域[1]。近年来,全球工业生物技术发展迅猛,成为继医药生物技术和农业生物技术之后,国际生物技术发展的第三次浪潮,占有重要的国际地位。其中,工业生物发酵是工业生物技术的关键,是工业生物技术规模化生产必需的基本操作单元。我国已成为世界生物发酵产业大国,2018年生物发酵行业主要产品产量约2 961.6万t,与2017年相比增长约4.1%;总产值2 472亿元,同比增长3.4%。生物发酵主要行业、主要产品出口量491.09万t,出口额53.53亿美元,较2017年同期增长25.1%[2]。
中国生物发酵产业“十三五”发展规划[3]指出,加快发展和壮大生物发酵产业、以充分利用可再生资源、解决国民经济发展中可能面临的资源短缺等问题、构建可持续的经济发展之路成为必然选择。然而,当前我国的工业生物发酵产业的产品以中低端为主,附加值较低,品质远远不及同类其他国际品牌,其中的原因离不开生产控制技术落后、发酵过程优化和相关技术装备的智能化水平较低等因素。
微生物发酵过程集合了化工过程与生物代谢过程的特点,系统的复杂性导致单凭经验来控制生产已经远远不能满足实际的需求,如控制不当就会造成较大的损失;而且,传统的经验控制方法无法实现智能制造。而数学和计算机技术的快速发展为复杂发酵过程的分析和监控提供了可能。对微生物细胞及其反应器进行严格的数学描述将有助于加深对发酵系统的理解,并在数字细胞模型中产生强大的作用。同时,在数学模拟的指导下也将会有效提高合成生物构建的效率[4]。因此,借助数学和计算机对发酵过程建模和模拟越来越受到人们的关注,也使其成为智能生物制造产业发展的核心技术之一。
本文试图从工业发酵系统的特点、数学模拟的发展历史、数学模型的分类和特点、用途等方面作深入阐述,并展望全发酵系统模拟的发展趋势,为数学模拟在工业发酵产业的应用奠定基础。
1 工业发酵系统的特点
工业发酵系统是由微生物、培养介质、反应器等组成,微生物的生命活动是该系统的主体(图1)。其特点主要有以下几个方面:1) 发酵过程往往比化学过程更复杂。细胞代谢过程是由DNA、mRNA和蛋白质等分子参与的,一些随机效应导致细胞代谢的波动。这些波动包括启动子激活或失活以及mRNA和蛋白质的合成和衰变、基因产物如RNA聚合酶、核糖体和某些蛋白质等的在基因、代谢网络和细胞等尺度的波动。同时,在工业反应器中也存在不完全混合或分散以及环境的噪声涌入,容易导致细胞内代谢网络路径的通量分布、产品产量和发酵稳定性等方面的差异。2) 菌体的生长、产物生成均呈非线性。3) 除部分常规参数例如温度、pH等可以实现实时在线测量以外,大部分数据难以实现实时在线测量。这一过程的复杂性导致工业发酵系统具有非线性和时变性的特点,发酵体积越大越容易受到体系流体力学的影响;生物反应器是一种不均匀的流场,存在着温度、底物浓度、剪切力和溶解氧等的不同,导致体系中的微生物代谢受到反应器和自身代谢物的互相影响,而表现出时变性。

图1 发酵系统组成与交互
2 数学模型的发展历程
20世纪60年代Bird等将数学模拟的方法应用到化学工程中[5]。1973年Aiba等出版的《Biochemical Engineering》首次将化学工程的动力学模型的方法引入到生物过程中,将早期的描述性、经验性的方法发展到严格的数学推理[6]。Arnold Fredrickson等于1970年将结构和隔离引入到细胞研究中,并提出4种不同的隔离和结构组合或缺失,方便地将最常见的数学描述和实验类型划分为4个不相交的类别 (结构隔离模型、结构非隔离模型、非结构非隔离模型和非结构隔离模型,见表1)[7]。
生物化学过程是建立在热力学、动力学和化学计量学三大基本原理的基础上。热力学理论对于化学和生物化学过程特别重要,它表征了一个封闭系统的物质、能量、功和热能之间的关系,可以用热力学分析哪些过程在热力学上是否可行。但是,热力学研究几乎排除了反应的时间影响,其结论只关注反应是否可行,而无法说明是在多长时间发生的反应。而反之,动力学研究对于能量的关注较少,其主要关注生物化学反应的时间观,而且动力学分析还忽略了空间和混合程度的影响。最早期的动力学研究策略是采用微分方程描述状态变量的改变,又因为忽略了空间的影响,就可以采用常微分方程来表示,典型的代表就是描述单底物酶催化反应动力学的Michaelis- Menten方程。但是,发酵过程中可能存在着底物添加等的脉冲行为、发酵过程中的各种随机因素的干扰无时无处不在,导致线性动力学理论已经不能满足对客观实际的发酵系统的全面了解。近30–40年以来,非线性动力学理论特别是脉冲动力系统、随机动力系统、时滞动力系统和混杂系统等多种理论工具的不断完善和计算机代数、数值模拟和图形技术的发展,使得非线性动力系统得到了飞速的发展。建立一个工业发酵体系完整动力学模型的另外一个有效方式是系统化学计量学研究,而这一基础是细胞内普遍存在的代谢途径的基本生化过程。其中包括了代谢通量分析、流量平衡分析等代谢网络分析的方法[8]。
以上的研究都是建立在生物化学机理的基础上的,但是,因为发酵过程的复杂性很难建立足够精确、简单、灵活、适应性强、速度快、鲁棒性强的机理模型。随着计算机技术的发展和发酵反应器在线测量技术的发展,基于人工智能(AI) 的方法开始用于重要变量的在线估计和生物反应器的最优控制,例如人工神经网络[9]、遗传算法[10]和模糊逻辑[11]等已在不同的研究中得到应用。尽管它们优于经典的建模和控制方法,但是人工智能方法是一种黑箱模型,并不关注微生物的生理状态和代谢机理。因此,这种模型需要大量的数据来训练,而且模型也仅仅局限于其训练的领域,无法拓展。这些弱点催生了将人工智能与机理模型相结合的混合模型,这种混合模型能够更加准确地模拟发酵的实际过程[12]。
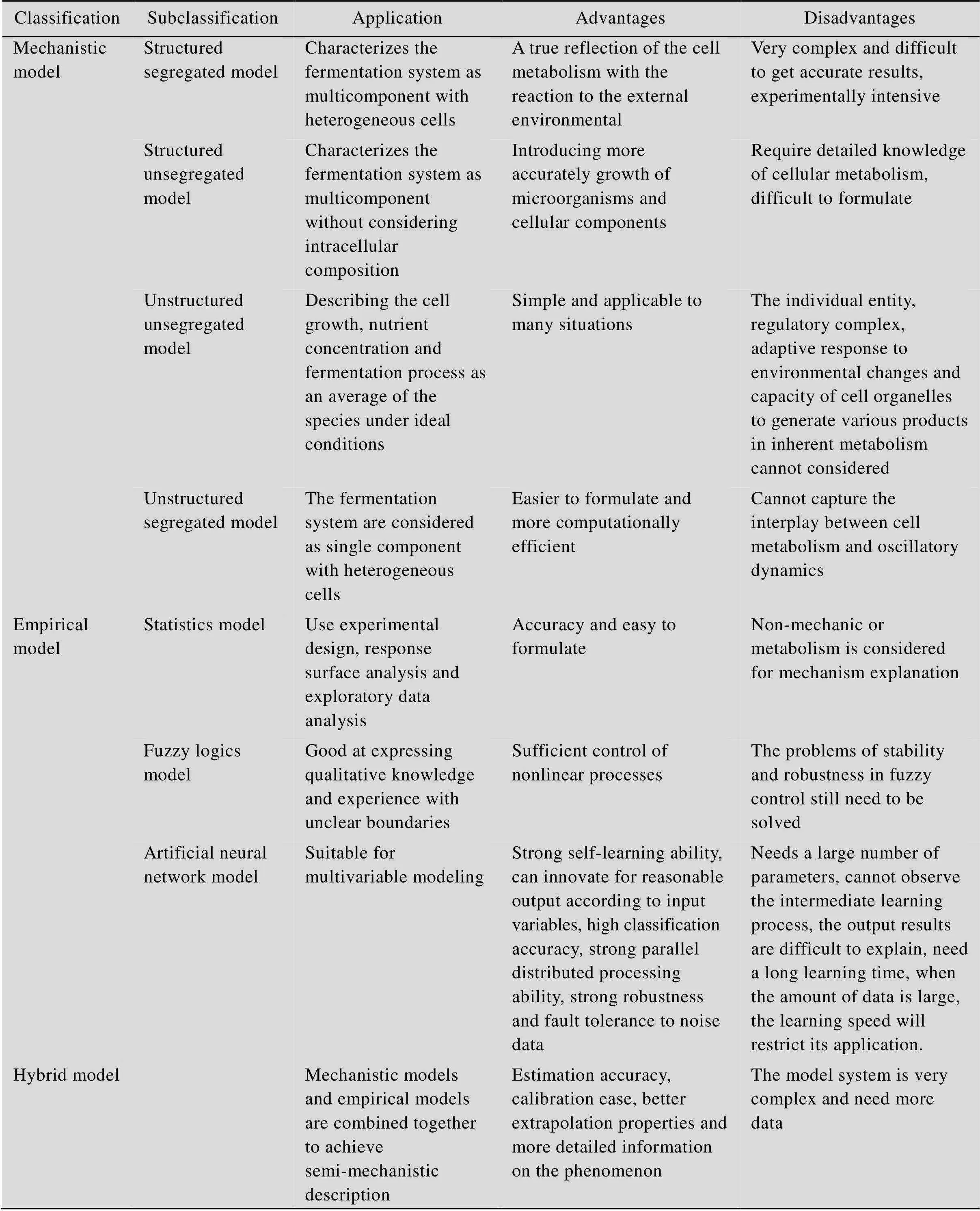
表1 数学模型的分类
在工业发酵的复杂体系中,还要关注体系中的流体力学情况。张嗣良等团队提出了将反应器流场特性与细胞生理特性相结合的发酵工程放大技术,通过对反应器的计算流体力学(Computational fluid dynamics,CFD)的模拟和仿真结合菌体生理特性的相关性分析,寻找过程放大的敏感参数实现发酵过程的放大[13]。
3 工业发酵模型与简介
将工业发酵过程模拟方法分为机理模型、实验模型和混合模型3种类型(表1)。
3.1 机理模型
机理模型是根据发酵系统的组成和运行机理对系统内部模拟的数学公式。例如,在好氧发酵中,主要成分是底物、氧气、细胞质量、反应器体积、底物和气流,而主要机制是微生物生长、传质(曝气) 和混合(底物、pH控制试剂)。它以确定性原理为基础,在给定初始条件下可以预测发酵系统的行为。
3.1.1 非结构非隔离模型
模型的基本假设认为发酵反应器的环境是均匀的,也不考虑细胞之间的差异,并将细胞及其成分描述为溶液中的单一成分。该模型基于细胞质量、底物、代谢物的产生和消耗的守恒方程,来表征微生物代谢的表观速率,因此就有细胞生长速率、营养吸收速率和代谢物生成速率等参数。现代微生物生长动力学起源于Monod方程,该方程认为细胞的比生长速率与限制性基质的浓度关系可用=max/(+) 来表示,其中,为菌体的生长比速,为限制性基质浓度,为半饱和常数,max为最大比生长速度。
这种方程表述简单,应用范围广泛,目前还有较广的应用[14-15]。但是它仅仅用于细胞生长速度较慢和细胞密度较低的环境下,不能考虑个体、调节复杂、对环境变化的适应性反应以及细胞器在固有代谢中产生各种产物的能力。
3.1.2 非结构隔离模型
微生物在不同的生长时期具有不同的形态和生产能力。非结构化隔离模型通过单个细胞的细胞大小或菌龄等来表征细胞,而不考虑细胞内成分变化[16]。该模型基于典型的微生物细胞周期——DNA合成(S)、有丝分裂(M) 和两次间期(G1和G2),这些阶段具有不同的细胞活动、形态甚至机理特性。一个新的细胞进入间期1期(G1) 的循环,然后进入DNA合成阶段(S)。完成S期后,细胞进入间期2期(G2),然后在有丝分裂期(M) 开始细胞分裂过程。两个子细胞从G1到M重复相同的周期[17]。基于细胞周期的分离模型将生长、代谢过程和产物形成的动力学与各阶段种群的分布联系起来。Zhang等采用非结构分隔模型,将细胞质量分布的种群平衡方程(Population balance equation,PBE) 与底物速率限制的质量平衡耦合研究了导致这些周期解的分岔,解释了酵母出芽过程中的自激振荡现象[18]。Jarzebski等将酵母菌连续发酵产乙醇过程中的细胞分为活性、无活性和死细胞3种,建立了综合考虑底物和产品抑制的动力学非结构分离模型来预测实验的振荡和稳态行为[19-20]。
3.1.3 结构非隔离模型
结构非隔离模型考虑了细胞的内部结构和组成,使用细胞生长及其代谢来描述更准确的生长速率。该模型一般分为形态结构模型、化学结构模型、基因结构模型和代谢结构模型[21]。
形态结构模型常用来描述重要生产生物体、丝状真菌的生长,并区分菌丝元素的不同区域[22-23]。
化学结构模型考虑了化学物质在发酵动力学中的作用,并将所有的速率参数考虑在内。Garcia-Ochoa等提出了一种同时考虑碳源和氮源代谢的黄原胶生产化学结构动力学模型,该模型考虑了8个集中反应(氨基酸的合成、未形成和形成碱基、核酸合成、RNA和DNA、黄原胶的产生、总糖代谢、氧化磷酸化和维持能量) 和8个关键化合物(生物量、铵、RNA、DNA、细胞内蛋白质、黄原胶、蔗糖和溶氧)。该动力学模型能够与实验数据非常一致地描述之前在所有运行中提到的8种关键化合物的浓度演变。此外,结构化动力学模型能够预测系统在某些操作条件变化时的行为,如温度和初始氮浓度,以及不同的氧气输送速率,根据操作条件和介质成分(氮) 预测不同的黄原胶生产速率[24]。
基因结构模型是建立在基因分子机制基础上的,该模型包括操作调控基因的表达速率和转录、翻译和折叠过程的动力学方程。Koh等提出了一种基于已知的阻遏物蛋白、辅阻遏子和诱导物分子相互作用的TRP操纵子遗传结构数学模型,该模型定性和定量地模拟了这些调控物对克隆基因产物抑制和表达程度的影响。基于该模型的计算可以预测有效抑制的最佳载脂蛋白和色氨酸水平,同时还可以预测诱导低质粒和高质粒拷贝数克隆所需的对吲哚丙烯酸浓度。利用这个模型还可以解释研究人员在研究TRP启动子时所观察到的似乎不正常的、有时是矛盾的现象[25]。Lee和Bailey构建了大肠杆菌lac操纵子功能的遗传结构模型[26],Keasling等构建了结构lac操纵子模型[27]。当这类模型与代谢物水平的描述结合时,可能预测基因表达的变化。
代谢结构模型可以更好地理解过程调节机制,如反馈调节。该模型以主要代谢途径为基础,大多数情况下包含在代谢流量分析(Metabolic flux analysis,MFA) 中。在代谢物浓度变化的情况下,网络结构将反应和代谢物浓度作为矩阵阵列表示。Hatzimanikatis等进一步提出了这一概念,并建立了大肠杆菌糖酵解动力学模型,该模型与混合整数线性规划优化程序相结合,以预测网络酶的最佳调节特性[28]。然而,对于无法获得机理信息的大型网络、基因、代谢等结构描述可能就会比较困难。
3.1.4 结构隔离模型
结构隔离模型综合考虑细胞组成变化和细胞之间的差别,因此结构隔离模型非常复杂需要复杂的细胞内测量技术(如流式细胞仪) 来对其可行性进行验证[29]。Henson建立了一个描述细胞外环境的简单结构化分离模型,并对其进行了评价[30]。该模型解释了与葡萄糖基质细胞生长有关的3个最重要的代谢途径。与完全非结构化模型相比,该模型的主要优点是可以将细胞外变量的预测直接与实验数据进行比较。因此,该模型结构非常适合于从可用的细胞外测量中确定未知的模型参数。Fordyce和Rawlings构建了一个分离模型来预测地衣芽孢杆菌在液体发酵系统中生长和分化的有效性[31]。分离模型解释了芽孢杆菌生命周期的3种形态。利用年龄-种群模型对孢子囊生物量进行了表征,以反映孢子形成的年龄依赖过程。提出了控制营养细胞繁殖率、孢子萌发率、产孢率和底物消耗率之间的关系。
3.2 经验模型
被称作白箱模型的机理模型虽然能够展示实际发酵过程的内部反应机理,然而,由于生物发酵过程涉及细胞的生长繁殖和代谢,存在着严重的非线性、时变性和不确定性。因此,在实际发酵过程中的机理建模是十分困难的,而且需要大量的试验对机理模型进行参数辨识和估计,在实际应用中难以做到。而且,一些生物变量很难在线检测,往往需要离线采样分析,不能及时反映和跟踪过程变化,加之对许多生化过程的代谢途径尚不清楚,难以得到准确的机理模型。因此,需要一种更加有效的建模方法[8]。综合以上的问题,需要一种不考虑发酵过程机理的建模方法,仅仅考虑其输入的变量(温度、压力、pH、溶氧、补料速率、基质浓度、产物浓度等) 和输出的变量(建模的目的变量,如产物浓度、基质浓度、菌体浓度) 的模型,建立在统计学基础上的模型营运而生。该模型只需要建立输入和输出的相关关系,其主要的方法有回归模型、模糊逻辑和人工神经网络等。
3.2.1 回归模型
回归模型可以定量地描述某一现象和某些因素之间的函数关系,将各变量的已知值代入回归方程可以求出因变量的估计值,从而可以进行预测等相关研究。该方法在发酵过程模拟中得到了大量的应用。Wu等研究表明非线性回归模型结合拉曼光谱检测可以作为发酵过程的快速监测方法[32]。Azman等建立了一个二阶多项式回归模型来优化农业工业废水制氢性能[33]。
3.2.2 人工神经网络
人工神经网络(Artificial neural network,ANN) 是20世纪80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象,建立某种简单模型,按不同连接方式组成不同的网络,其机理可参考文献[34-38]。
在Elnekave等的研究中采用3种不同的神经网络,即前馈反向传播神经网络(Feed forward back-propagation neural network,BPNN)、径向基函数神经网络(Radial basis function,RBF) 和广义回归神经网络(Generalized regression neural network,GRNN),模拟了流量、体积负荷、初始化学需氧量和初始总悬浮物对最终化学需氧量和最终总悬浮物的影响。结果表明,BPNN的预测结果最好,平均偏差在实验值的6.4%–15.6%之间。优化后的模型验证发现能够达到较高的COD去除效率(77%–79%),同时产生880–11 000 m3/d的沼气[39]。
但是,神经网络模型需要大量的参数,不能观察中间学习过程,输出结果较难解释,会影响到结果的可信度,需要较长的学习时间,当数据量较大的时候,学习速度会制约其应用。
3.2.3 模糊逻辑模型
模糊逻辑(Fuzzy logic) 指的是模仿人脑的不确定性概念判断、推理思维方式,对于模型未知或不能确定的描述系统,以及强非线性、大滞后的控制对象,应用模糊集合和模糊规则进行推理,表达过渡性界限或定性知识经验,模拟人脑方式,实行模糊综合判断,推理解决常规方法难以解决的规则型模糊信息问题。其机理可以参考文献[40]。Márquez-Vera等基于线性矩阵不等式构建了一种模糊控制和模糊观测器,用此模糊模型对状态反馈控制器和观测器增益进行了调整,可以进行状态反馈以控制产品浓度[41]。Flores-Asis等[42]采用模糊逻辑模型的方法对某禽类加工厂污水处理的污泥进行了热预处理,确定了影响沼气产量和甲烷产量最大的变量,以加速污泥厌氧消化过程。设计的模糊逻辑模型包括688条推理规则,预测数据与实验数据的相关性为99.3%,沼气变量的相关性为97%。利用响应面模型对模糊逻辑模型的预测进行了分析,得出了在沼气生产中,温度和操作时间变量是相互决定的结论。这项研究为专家决策支持系统的设计提供了可靠的方法。
3.3 混合模型
发酵代谢反应是由结构和功能复杂的分子调节的,这些分子在遗传水平上对噪声敏感,其变异会显著影响微生物表型;而且,细胞代谢过程也对环境变化作出反应。因为缺乏基本知识或是因为其复杂性,单独的机理模型难以描述整个发酵过程。面对复杂的生物反应器的噪声和空间变化,经验模型常被用来模拟宏观微生物行为。然而经验模型不包含细胞过程的生理特征,很难为这些模型的参数提供精确的机理解释。而且,没有一个模型能够同时考虑细胞内和细胞外的噪声,因此有必要将机理模型与人工智能模型相结合来表述微生物过程[43]。
混合模型已被公认为生物过程分析的一种经济有效的方法。最常用的混合模型是基于质量平衡方程(如传统的第一原理方法) 与人工神经网络反应动力学模型相结合的方法[44-45]。Oliveira提出了一种将第一原理建模与人工神经网络相结合的生物反应器混合模型结构:用一组质量平衡方程描述生物反应器系统,用神经网络和机理模型共同来表示细胞群系统。基于这种混合结构的数学公式,他们从系统工程的角度对发酵系统进行了分析[45]。
混合模型可以集成更多的参数和信息,因此可以实现更高的精度、更少的迭代次数和更低的开发成本。这些复合模型原则上应该像智能模型一样具有适应性、灵活性和自我调节性,但也具有机理模型的基本生物学基础。
3.4 流体力学模拟
发酵系统是由微生物和反应器组成的,微生物的生长和产物的形成是由细胞内部代谢和反应器环境之间的交互作用决定的。因此,对发酵过程建模时,除了关注细胞内功能单元的复杂相互作用以外,还要关注生物反应器的结构与内部流场情况(混合和传质强度的时空变化、各种基质和产物的浓度梯度等)。因此,如果将微生物和反应器作为一个系统来看待,模型需要加入反应器的流场情况。目前,反应器流场的模拟一般用计算流体力学来开展。CFD的基本思想是求解反应器中流体的运动方程(即Navier-Stokes方程),这些方程描述了流体的质量守恒和动量平衡。Wolf等提出了基于拉格朗日-欧拉模型的方法,其中液相被视为连续体(欧拉),分散相借助拉格朗日表示进行跟踪[46]。还有研究采用混合方法,将多区域模型与CFD计算结合起来[47]。Delvigne等构建了一个完整的发酵放大/缩小的模拟方法,该方法将计算流体动力学、代谢通量分析和Agent-based Modelling (ABM) 关联起来,以便更好地理解非均匀环境中的细胞生命行为[48]。
3.5 组学指导下的数学建模
随着组学时代的到来,描述微生物生长的模型的覆盖范围和深度达到了一个新的水平,从而开创了组学建模方法的时代。人们开始试图建立代谢组、蛋白质组和基因组之间的关系。代谢网络的基因组尺度重构与基于约束的建模相结合是微生物系统生物学中日益流行的方法。虽然重建主要基于基因组学数据,但它是通过对相关生物体的生物化学、遗传和/或生理学知识的反复修正将网络重建转化为一个数学模型,通常称为基因组尺度模型(GEM),通过一系列基于约束的方法,如通量平衡分析,可以进行定性和定量分析。这有助于进一步完善网络重建,并为基因型-表型关系提供有价值的见解[49]。
从细胞生长的角度来看,与简单的非结构化生长模型相比,基因组尺度模型使用更详细和准确的机制(以及相关的数学表达式)。Yizhak等将代谢组学和蛋白质组学数据整合到Michaelis-Menten动力学表达式中,使用体外m参数比不考虑动力学的方法更准确地预测通量变化[50]。Cotten等[51]通过整合通量组学、蛋白质组学和代谢组学数据,估算了大肠杆菌中心代谢动力学模型中的动力学参数。
4 发酵过程数学模型用途
4.1 发酵过程的优化、控制与故障诊断
发酵过程本身比较复杂,优化、放大与控制的难度都较大;批次间的重复性很差,极易造成产量和质量的波动。同时,随着发酵原料成本的增加、环保意识的增强,发酵过程的精准控制要求越来越高。因此,常规、简单的控制方法已不能满足生产的需求。大量的研究将数学模型用于发酵过程优化、放大、控制与故障诊断中。这将会为产业的发展提供智能发酵技术支持。
4.2 为途径设计与理性改造提供策略方案
随着合成生物学技术的发展,利用微生物发酵生产各种不同的化学品成为当前研究的热点。常规方法从能够产生少量所需化学品的菌株到获得一种符合商业可行工艺要求的菌株需要3–5年的时间和超过5 000万美元的投资。随着新的基因编辑技术的出现(例如CRISPR/Cas9技术),目前的挑战已经变为如何为菌种改造提供技术方案[52]。将分子、蛋白、网络、细胞和反应器的大数据采用机理模型和人工智能模型的手段整合为一个全局模型将会为途径的改造提供全局模拟。这种模拟代谢将会为化学品的生产途径和代谢网络的改进提供信息。例如,全基因组代谢模型与整个代谢网络中的化学计量学相耦合,非常适合于代谢工程设计[53]。
4.3 全细胞生命现象的解析
工业发酵不同于常规细胞生命活动,微生物细胞除了在生产中表现出稳定性、鲁棒性等优良特性以外,它还要适应不同发酵规模下空间的不均一性的变化。而这些现象的解析,除了常规方法在基因层面的支离破碎的信息以外,基于模型模拟的细胞整体生命活动特性的解析就显得尤为重要。它们可以解析细胞的自组织空间模式、动力学和流体响应信息,从个体和群体层面上增进对发酵系统的理解。
5 模型的评价
模型是否能够服务于对微生物代谢的理解、工艺过程的优化和控制应该成为评价一个模型的重要指标,即为“目标适用性”[54]。一个微生物发酵系统非常复杂,目前的技术还不可能面面俱到实现完美的模拟,但是如果实现了“目标适用性”即可以认为该过程模拟达到了目的。
良好的建模规范(Good modeling practice,GMoP) 将不确定性和敏感性分析与建模相结合是将模型构建过程或模型后续应用和解释中的错误风险降至最低的必要条件。与模拟模型预测相关的不确定性通常被分为:(a) 描述随机系统所需的模拟模型的随机组成部分产生的随机不确定性;(b) 主观(或输入) 不确定性,表示对用作模型输入的固定值的不完全了解;(c) 与数学相关的结构不确定性公式或模型结构。灵敏度分析是对不确定度分析的补充,可以对参数重要性进行排序,以减少最有影响的参数的不确定性,而不是将实验工作浪费在对模型输出影响很小或没有影响的参数上[55],以此可以分析出模拟需要的重要参数和条件。
6 总结与展望
工业发酵过程拥有一个非常复杂的代谢过程,涉及大量的代谢反应网络以及相关的基因调控和环境影响。而数学建模从早期现象学描述发展到代谢网络和代谢网络的系统建模,从简单的基因调控发展到系统级整合的尝试将会使研究人员可以深入了解复杂的发酵过程,并能实现过程的优化与控制。而数学模拟的终极目标是要建立全发酵系统的细胞、反应器和过程的模型,也就是数字化的生产系统(包括细胞、反应器及其交互系统),而不仅仅是数字化细胞。
微生物数字细胞模型的研究因为计算能力、未知的代谢机理等因素的限制,进展并不顺利,截至目前仅有3个细胞模型:1) 由Shuler开发的大肠杆菌模型,可以描述14个关键变量的细胞功能[56];2) 由Tomita等开发的大肠杆菌ECELL模型,允许用户根据特定的需求模拟细胞功能[57];3) 由Karr等开发的生殖支原体模型,代表了整个细胞最全面的数学模型[58]。
工业发酵系统中微生物和反应器是一种交互共存的系统,微生物细胞本身、发酵反应器和外环境对整个体系的影响非常大。因此,发酵过程建模应综合考虑微生物细胞内部体系、交互体系和反应器体系的参数。如能建立全系统细胞模型,将会实现全发酵系统的模拟计算,为菌种途径改造、发酵优化和反应器设计等提供全方位的计算和信息支持。但是,以上3个细胞模型(大肠杆菌模型[56]、大肠杆菌ECELL模型[57]和支原体模型[58]) 仅仅是建立在细胞中不同生物学过程的简单描述的基础上,并未考虑外界环境对细胞模型的影响。为了提高工业发酵模型的预测和控制能力,首先需要扩展相关分子、细胞和反应器信息的系统级整合,包括细胞对反应器时空的响应、基因调控程序及其环境信号激活调控机制等;其次对现有模型也要进行扩容,除了批量发酵数据以外,还应包括使模型适应连续生产或其他发酵系统。而这些信息的整合需要建立更加复杂的模型框架,这对当前细胞代谢机理和数据处理能力都提出了巨大的挑战。
[1] An in-depth analysis of the current situation and prospects of China's industrial biotechnology industry [EB/OL]. [2018-01-18]. http://www.sohu.com/a/ 217371839_777213.深度解析中国工业生物技术行业发展现状及前景[EB/OL]. [2018-01-18]. http://www.sohu.com/a/ 217371839_777213.
[2] Summary of the second eighth council and the second eighth standing council of China Biological Fermentation Industry Association[EB/OL]. [2019-04-19]. http://www.clii.com.cn/xxhdt/201904/t20190419_3934099.html.中国生物发酵产业协会二届八次理事会暨二届八次常务理事会会议纪要[EB/OL]. [2019-04-19]. http:// www.clii.com.cn/xxhdt/201904/t20190419_3934099.html.
[3] Full text of the 13th Five-Year Plan for the development of bio-industry[EB/OL]. [2017-01-16]. http://www. biotech.org.cn/information/145003. “十三五”生物产业发展规划全文[EB/OL]. [2017-01- 16]. http://www.biotech.org.cn/information/145003.
[4] Straathof AJJ, Wahl SA, Benjamin KR, et al. Grand research challenges for sustainable industrial biotechnology. Trends Biotechnol, 2019, doi: 10.1016/j.tibtech.2019.04.002Get.
[5] Bird R, Stewart W, Lightfoot E. Transport Phenomena. 4th ed. New York: John Wiley & Sons, 1960.
[6] Aiba S, Humphrey AE, Millis NF. Biochemical Engineering. New York and London: Academic Press Inc., 1973.
[7] Fredrickson AG, Megee RD, Tsuchiya HM. Mathematical models for fermentation Processes// Perlman D, Ed. Advances in Applied Microbiology. New York and London: Academic Press, 1970: 419–465.
[8] Gao XJ, Qi YS, Wang P. Modeling, Optimization and Diagnosis of Biological Fermentation Process. Beijing: Science Press, 2016: 277 (in Chinese).高学金, 齐咏生, 王普. 生物发酵过程的建模、优化与故障诊断. 北京: 科学出版社, 2016: 277.
[9] Hernández G, León R, Urtubia A. Application of computational intelligence techniques for forecasting problematic wine fermentations using data from classical chemical measurements//Panda SK, Shetty PH, Eds. Innovations in Technologies for Fermented Food and Beverage Industries. Cham: Springer, 2018: 317–330.
[10] Esfahanian M, Shokuhi RA, Khoshhal S, et al. Mathematical modeling of continuous ethanol fermentation in a membrane bioreactor by pervaporation compared to conventional system: Genetic algorithm. Bioresour Technol, 2016, 212: 62–71.
[11] Baghban A, Adelizadeh M. On the determination of cetane number of hydrocarbons and oxygenates using Adaptive Neuro Fuzzy Inference System optimized with evolutionary algorithms. Fuel, 2018, 230(5): 344–354.
[12] Galvanauskas V, Simutis R, Lübbert A. Hybrid process models for process optimisation, monitoring and control. Bioproc Biosyst Eng, 2004, 26(6): 393–400.
[13] Zhang SL, Wang ZJ. Fermentation engineering research and technological progress. Biotechnology & Business, 2014, (2): 9–19 (in Chinese).张嗣良, 王泽建. 发酵工程研究与技术进步. 生物产业技术, 2014, (2): 9–19.
[14] López-Meza J, Araíz-Hernández D, Carrillo-Cocom LM, et al. Using simple models to describe the kinetics of growth, glucose consumption, and monoclonal antibody formation in naive and infliximab producer CHO cells. Cytotechnology, 2016, 68(4): 1287–1300.
[15] Sin G, Ödman P, Petersen N, et al. Matrix notation for efficient development ofmodels within PAT applications: Integrated modeling of antibiotic production with. Biotechnology and Bioengineering, 2008, 101(1): 153–171.
[16] Zamamiri AM, Zhang Y, Henson MA, et al. Dynamics analysis of an age distribution model of oscillating yeast cultures. Chem Eng Sci, 2002, 57(12): 2169–2181.
[17] Van Dolah FM, Ramsdell JS. Maitotoxin, a calcium channel activator, inhibits cell cycle progression through the G1/S and G2/M transitions and prevents CDC2 kinase activation in GH4C1 cells. J Cell Physiol, 1996, 166(1): 49–56.
[18] Zhang YC, Zamamiri AM, Henson MA, et al. Cell population models for bifurcation analysis and nonlinear control of continuous yeast bioreactors. J Proc Control, 2002, 12(6): 721–734.
[19] Paz Astudillo IC, CAlzate CAC. Importance of stability study of continuous systems for ethanol production. J Biotechnol, 2011, 151(1): 43–55.
[20] Jarzębski AB. Modelling of oscillatory behaviour in continuous ethanol fermentation. Biotechnol Lett, 1992, 14(2): 137–142.
[21] Bapat PM, Bhartiya S, Venkatesh KV, et al. Structured kinetic model to represent the utilization of multiple substrates in complex media during rifamycin B fermentation. Biotechnol Bioeng, 2006, 93(4): 779–790.
[22] Riley GL, Tucker KG, Paul GC, et al. Effect of biomass concentration and mycelial morphology on fermentation broth rheology. Biotechnol Bioeng, 2000, 68(2): 160–172.
[23] Nielsen J, Villadsen J. Modelling of microbial kinetics. Chem Eng Sci, 1992, 47(17/18): 4225–4270.
[24] Garcia-Ochoa F, Santos VE, Alcon A. Chemical structured kinetic model for xanthan production. Enzym Microb Technol, 2004, 35(4): 284–292.
[25] Koh BT, Yap MGS. A simple genetically structured model ofrepressor-operator interactions. Biotechnol Bioeng, 1993, 41(7): 707–714.
[26] Lee SB, Bailey JE. Genetically structured models forpromoter-operator function in thechromosome and in multicopy plasmids:operator function. Biotechnol Bioeng, 1984, 26(11): 1372–1382.
[27] Carrier TA, Keasling JD. Investigating autocatalytic gene expression systems through mechanistic modeling. J Theoret Biol, 1999, 201(1): 25–36.
[28] Hatzimanikatis V, Bailey JE. Studies on glycolysis-I. Multiple steady states in bacterial glycolysis. Chem Eng Sci, 1997, 52(15): 2579–2588.
[29] Srienc F, Dien B. Kinetics of the cell cycle of. Ann New York Acad Sci, 1992, 665(1): 59–71.
[30] Mhaskar P, Hjortsø MA, Henson MA. Cell population modeling and parameter estimation for continuous cultures of. Biotechnol Progr, 2002, 18(5): 1010–1026.
[31] Fordyce AP, Rawlings JB. Segregated fermentation model for growth and differentiation of. AIChE J, 1996, 42(11): 3241–3252.
[32] Wu ZZ, Xu EB, Long J, et al. Measurement of fermentation parameters of Chinese rice wine using Raman spectroscopy combined with linear and non-linear regression methods. Food Control, 2015, 56: 95–102.
[33] Azman NF, Abdeshahian P, Al-Shorgani NKN, et al. Production of hydrogen energy from dilute acid-hydrolyzed palm oil mill effluent in dark fermentation using an empirical model. Int J Hydrogen Energy, 2016, 41(37): 16373–16384.
[34] Hopfield JJ, Tank DW. Computing with neural circuits: a model. Science, 1986, 233(4764): 625–633.
[35] Huang YQ, Kangas LJ, Rasco BA. Applications of artificial neural networks (ANNs) in food science. Crit Rev Food Sci Nutr, 2007, 47(2): 113–126.
[36] Zupan J, Gasteiger J. Neural networks in chemistry and drug design. Weinheim, Germany: Wiley-VCH, 1999: 9–36.
[37] Schalkoff RJ. Artificial neural networks. New York: McGraw-Hill, 1997.
[38] Rosales-Colunga LM, García RG, De León Rodríguez A. Estimation of hydrogen production in genetically modifiedfermentations using an artificial neural network. Int J Hydrogen Energy, 2010, 35(24): 13186–13192.
[39] Elnekave M, Celik SO, Tatlier M, et al. Artificial neural network predictions of up-flow anaerobic sludge blanket (uasb) reactor performance in the treatment of citrus juice wastewater. Pol J Environ Stud, 2012, 21(1): 49–56.
[40] Chen CH. Fuzzy Logic and Neural Network Handbook. New York: McGraw-Hill, 1996.
[41] Márquez-Vera MA, Ramos-Velasco LE, Balderrama- Hernández BD. Stable fuzzy control and observer via LMIs in a fermentation process. J Comput Sci, 2018, 27: 192–198.
[42] Flores-Asis R, Méndez-Contreras JM, Alvarado- Lassman A, et al. Analysis of the behavior for operation parameters in the anaerobic digestion process with thermal pretreatment, using fuzzy logic. J Environ Sci Health, Part A, 2019, 54(6): 592–602.
[43] Patnaik PR. Toward a comprehensive description of microbial processes through mechanistic and intelligent approaches. Biotechnol Mol Biol Rev, 2009, 4(2): 29-41.
[44] Chen L, Bernard O, Bastin G, et al. Hybrid modelling of biotechnological processes using neural networks. Control Eng Pract, 2000, 8(7): 821–827.
[45] Oliveira R. Combining first principles modelling and artificial neural networks: a general framework. Comput Chem Eng, 2004, 28(5): 755–766.
[46] Lin JH, Xian JY, Chu J, et al. Numerical simulation of bioreaction process based on Euler-Lagrange frame. Chemical Engineering (China), 2016, 44(6): 4–9, 47 (in Chinese).林骥晗, 夏建业, 储炬, 等. 基于Euler-Lagrange框架的生物反应过程的数值模拟研究. 化学工程, 2016, 44(6): 4–9, 47.
[47] Bezzo F, Macchietto S, Pantelides CC. General hybrid multizonal/CFD approach for bioreactor modeling. AIChE J, 2003, 49(8): 2133–2148.
[48] Delvigne F, Takors R, Mudde R, et al. Bioprocess scale-up/down as integrative enabling technology: from fluid mechanics to systems biology and beyond. Microb Biotechnol, 2017, 10(5): 1267–1274.
[49] Rau MH, Zeidan AA. Constraint-based modeling in microbial food biotechnology. Biochem Soc Trans, 2018, 46(2): 249–260.
[50] Yizhak K, Benyamini T, Liebermeister W, et al. Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model. Bioinformatics, 2010, 26(12): i255–i260.
[51] Cotten C, Reed JL. Mechanistic analysis of multi-omics datasets to generate kinetic parameters for constraint-based metabolic models. BMC Bioinformat, 2013, 14(1): 32.
[52] Nielsen J, Keasling JD. Engineering cellular metabolism. Cell, 2016, 164(6): 1185–1197.
[53] Bro C, Regenberg B, Förster J, et al.aided metabolic engineering of Saccharomyces cerevisiae for improved bioethanol production. Metabol Eng, 2006, 8(2): 102–111.
[54] Gernaey KV, Lantz AE, Tufvesson P, et al. Application of mechanistic models to fermentation and biocatalysis for next-generation processes. Trends Biotechnol, 2010, 28(7): 346–354.
[55] Sin G, Gernaey KV, Lantz AE. Good modeling practice for PAT applications: Propagation of input uncertainty and sensitivity analysis. Biotechnol Progr, 2009, 25(4): 1043–1053.
[56] Domach MM, Shuler ML. A finite representation model for an asynchronous culture of. Biotechnol Bioeng, 1984, 26(8): 877–884.
[57] Tomita M, Hashimoto K, Takahashi K, et al. E-CELL: software environment for whole-cell simulation. Bioinformatics, 1999, 15(1): 72–84.
[58] Karr JR, Sanghvi JC, Macklin DN, et al. A whole-cell computational model predicts phenotype from genotype. Cell, 2012, 150(2): 389–401.
Simulation of industrial fermentation: current status and future perspectives
Demao Li, Wuxi Chen, Wei Guo, and Chaofeng Li
Tianjin Key Laboratory for Industrial Biosystems and Bioprocessing Engineering, Tianjin Institute of Industrial Biotechnology, Chinese Academy of Sciences, Tianjin 300308, China
Industrial fermentation is the basic operation unit of industrial biotechnology in large-scale production. Mathematical simulation of microbial cells and their reactors will help deepen the understanding of microorganisms and fermentation processes, and will also provide solutions for the construction of new synthetic organisms. In this paper, the characteristics of industrial fermentation system, the development of mathematical simulation, the classification, characteristics and functions of mathematical models are described in depth, and the development trend of whole fermentation system simulation is prospected.
industry biotechnology, fermentation, modeling and simulation, mechanistic model, empirical model, hybrid model
10.13345/j.cjb.190249
李德茂 博士,中国科学院天津工业生物技术研究所研究员,硕士生导师。天津市利用3年时间引进千名高技术人才获得者、中国科学院青年创新促进会会员、天津市滨海新区“131”创新型人才培养工程第二层次人才。曾获国家海洋局海洋创新成果奖二等奖、海洋工程科学技术奖二等奖。研究方向为工业发酵生物学。正式发表学术论文91篇,含第一作者或通讯作者SCI文章32篇;出版专著1部。获得授权专利16项 (包括美国专利1项);主持包括科技部国际合作重点项目、国家重点研发计划子课题等项目10余项。

李德茂, 陈吴西, 郭蔚, 等. 工业生物发酵过程模拟:进展与发展趋势. 生物工程学报, 2019, 35(10): 1974–1985.
Li DM, Chen WX, Guo W,et al. Simulation of industrial fermentation: current status and future perspectives. Chin J Biotech, 2019, 35(10): 1974–1985.
June 12, 2019;
September 9, 2019
Supported by: National Key Research and Development Project (No. 2018YFA0902200), STS Project of the Chinese Academy of Sciences (No.KFJ-STS-ZDTP-065), Key Project of Tianjin (No. 14ZCZDSY00157).
Demao Li. Tel/Fax: +86-22-24828745; E-mail: li_dm@tib.cas.cn
国家重点研发计划 (No. 2018YFA0902200),中科院STS计划(No. KFJ-STS-ZDTP-065),天津市科技计划 (No. 14ZCZDSY00157) 资助。
(本文责编 陈宏宇)

