针对相位噪声的广义软判决辅助相位估计算法

吕心浩，李 焱，张浩波，周武杰，吴茗蔚，3

(1.浙江科技学院 信息与电子工程学院，杭州 310023；2.苏州工业园区 新国大研究院先进微电子器件中心，江苏 苏州 215123；3.浙江省信息处理与通信网络重点实验室，杭州 310027)

互联网和多媒体业务的发展使数据通信业务的需求快速增长，光纤通信中传统的强度调制/直接检测系统已不能满足人们对数据通信量的需求，相干光通信技术应运而生。随着高速模数转换技术和数字信号处理(digital signal processing, DSP)技术的发展，相干光通信不仅能提供更高的数据传输速率，而且可以利用DSP技术补偿光纤通信中的各种损伤。因此，相干光通信技术已成为最具发展潜力的光纤通信技术之一。近年来，如M进制正交幅度调制(multiple quadrature amplitude modulation，MQAM)等高阶的调制方式，因其频谱效率高，在相干光通信中得到了广泛的应用。但这种调制需要在相干检测之前进行准确的载波相位估计[1-2]。锁相环(phase locked loop，PLL)[3-4]是一种候选方案。然而，由于激光线宽增加和环路延迟，PLL在应用中受到了限制。早期研究人员将传统的M次幂载波相位估计算法[5-7]用于相干光M进制相移键控(multiple phase shift keying，MPSK)，并结合差分编码，解决了相位模糊的问题，但这种方法使得差错加倍。此外，M次幂算法不适用于具有不等符号能量的调制方式。针对这两个问题，人们提出了可用于任意星座图的判决辅助最大似然(decision-aided maximum likelihood，DA-ML)相位估计算法[8-11]，DA-ML算法依赖于已接收信号的正确性，故该算法不适用于低信噪比情况。为了解决这一问题，软判决辅助最大似然(soft decision-aided maximum likelihood，SDA-ML)算法[12-15]使用发送信号的先验概率来代替接收信号的判决。DA-ML算法和SDA-ML算法性能优于M次幂算法，然而这两种算法是在逐块静态相位设下推导出的，受到块长度效应(block length effect，BLE)的较大影响，需要通过大量仿真来寻找最优的估计块长度。对此，本文引入多元高斯分布，针对线性激光相位噪声提出了广义SDA-ML相位估计算法，从而降低了对激光器线宽的要求。

1 系统模型

假设接收机实现理想定时同步、色散和偏振模型色散补偿、载波频率估计。在这种情况下接收信号，仅受到由发射机和本地振荡器(local oscillator，LO)引起的激光相位噪声及高斯白噪声(Additive White Gaussian Noise，AWGN)的影响[1]118。对于特定的符号周期Ts，第k个符号区间[kTs，(k+1)Ts]上接收到的采样信号模型r(k)由文献[1]119-[2]78171给出：

r(k)=s(k)ejθ(k)+n(k)。

(1)

本文采用与文献[12]3444相同的传输帧结构和滑动估计窗口，如图1所示。每帧插入Np个导频符号和Nm个连续数据符号，因此每比特信息的有效信噪比被定义为：

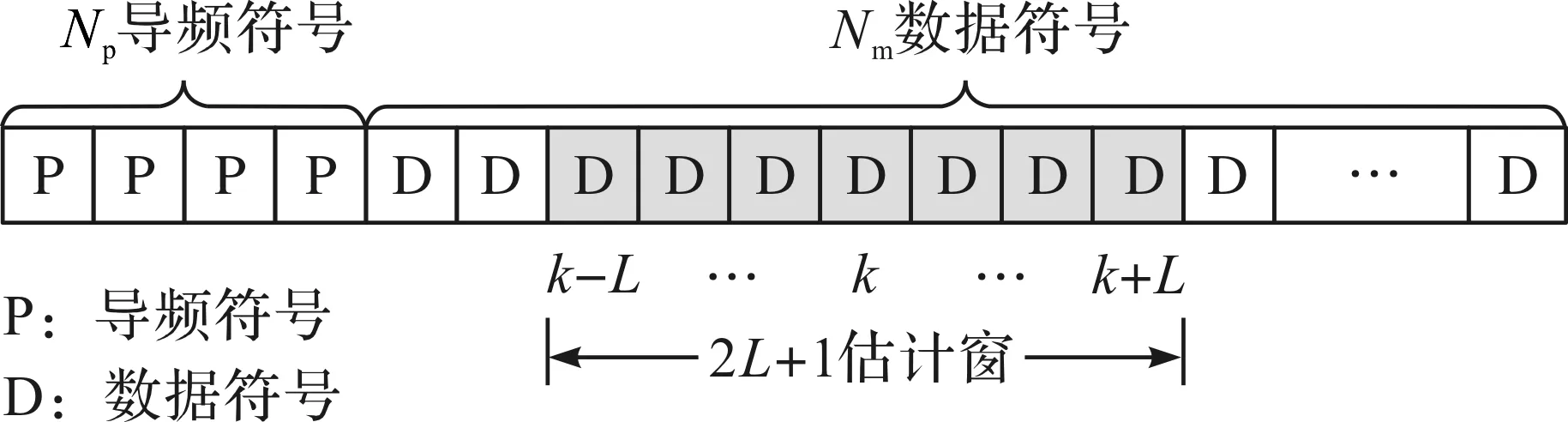
图1 传输帧结构和滑动估计窗口Fig.1 Transmitted frame structure and sliding estimation window

载波相位θ(k)通常用维纳过程来建模：

θ(k)=θ(k-1)+ν(k)。

(2)

式(2)中：{ν(k)}k为独立同分布(i.i.d)且均值为0的高斯随机变量[6]，方差为

(3)

式(3)中：Δν为发射机和LO激光器的3 dB线宽。通常认为相位噪声增量序列{ν(k)}k和高斯白噪声序列{n(k)}k是相互独立的。

2 广义SDA-ML估计算法

假设一个以时刻k为中心、长度为2L+1的对称估计窗口(图1)。这串信号可由以下数学模型表示：

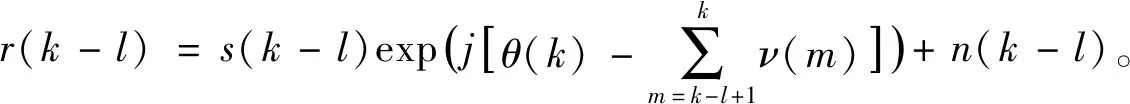
(4)

假设随机变量ν(m)的绝对值远小于1，考虑数学上的近似ex≈1+x，则式(4)可以简化为：

关于时间k处的相位估计通过最大化其似然函数Λ(k)得到。在接收估计窗r=[r(k-L)，…，r(k+L)]T(r是长度为2L+1采样信号向量)内，该似然函数Λ(k)被定义为以载波相位为条件的接收估计窗信号的联合概率密度函数，即：

(5)

利用全概率公式，通过对发送信号s(l)的所有可能情况求和，得到条件概率密度函数p(r|θ(k))，即：

(6)

式(6)中：s表示发送信号向量[s(k-L)，…，s(k+L)]T的所有可能假设；Pn为s(n)取值Ci的先验概率；K为(2L+1)×(2L+1)的协方差矩阵，其(n，m)元定义为

(7)

式(7)可以表示为：

(8)

为了简化似然函数Λ(k)，将接收估计窗分块为r1、r(k)和rr三部分。r1是r的左半部分，即r1=[r(k-L)，…，r(k-1)]T，rr是r的右半部分，即rr=[r(k+1)，…，r(k+L)]T，则r=[r1，r(k)，rr]T。从协方差矩阵K的形式可以看出，在θ(k)已知的条件下，r1、r(k)和rr是相互独立的。因此式(5)就可改写为：

(9)

由于似然函数的最大似然估计也可以从对数似然方程求得，式(9)可进一步表示为：

通过与式(6)相同的方式，得到条件概率密度函数p(r1|θ(k))，即：

(10)

式(10)中：s1表示发送信号向量[s(k-L)，…，s(k-1)]T的所有可能假设，Pn为s(l)取值Ci的先验概率，K1为r1的L×L协方差矩阵，即：

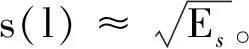
类似地，p(rr|θ(k))和p(r(k)|θ(k))可表示为：

(11)

式(11)中：sr表示发送信号向量[s(k+1),…,s(k+L)]T的所有可能假设，Kr为rr的协方差矩阵，即：

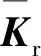
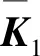
(12)

式(12)中：

(13)

(14)

式(13)～(14)中：

(15)

(16)

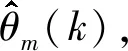
显然，估计阈值εθ是计算复杂度与相位估计精度的妥协。

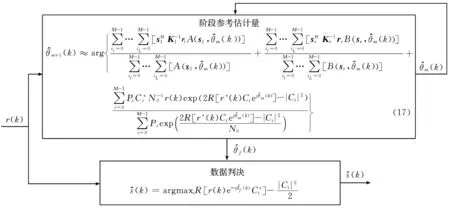
图2 广义SDA-ML接收机结构Fig.2 Generalized SDA-ML receiver structure

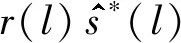
表1 计算复杂度比较Table 1 Comparison of computational complexity

3 仿真试验结果

由于广义SDA-ML相位估计算法在推导的过程中考虑了线性相位噪声的维纳过程对相位估计结果的影响，因此，它适用于较高线性相位噪声的情况。通过在MATLAB上的蒙特卡洛仿真试验，可将广义SDA-ML相位估计算法与DA-ML相位估计算法和传统的SDA-ML相位估计算法进行比较，比较误比特率(bit error probability，BEP)性能。调制方式包括二进制相移键控(Binary PSK，BPSK)，正交相移键控(Quadrature PSK，QPSK)，(1，3)-QAM和8QAM。在仿真试验中，由于DA-ML估计窗只有当前符号的左半部分，为了公平地比较各算法性能，故将DA-ML估计窗的长度调整至与SDA-ML和广义SDA-ML相同，即DA-ML估计窗长度为2L+1。

表2 迭代次数百分比分布Table 2 Percentage distribution of number of iterations %

表2列出了信噪比γb为0 dB、εθ=0.1时，QPSK调制下的SDA-ML和广义SDA-ML迭代次数的百分比分布。SDA-ML和广义SDA-ML的平均迭代次数接近，超过98%的迭代过程只需1次迭代就收敛于式(17)。

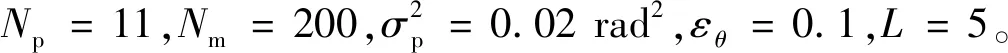
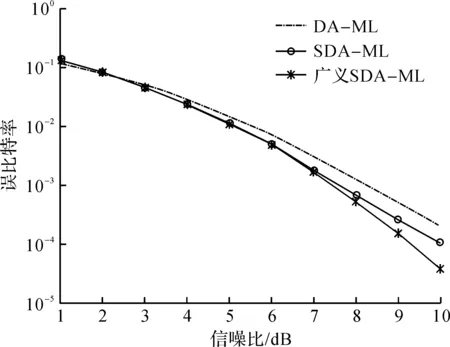
图3 BPSK下3种相位估计算法的BEP性能比较Fig.3 BEP performance comparison of BPSK with three phase estimation algorithms

为了更好地体现广义SDA-ML的BEP性能，将该算法用于(1，3)-QAM调制[12]3451和8QAM调制[16]，这两种调制方式的星座如图4所示。

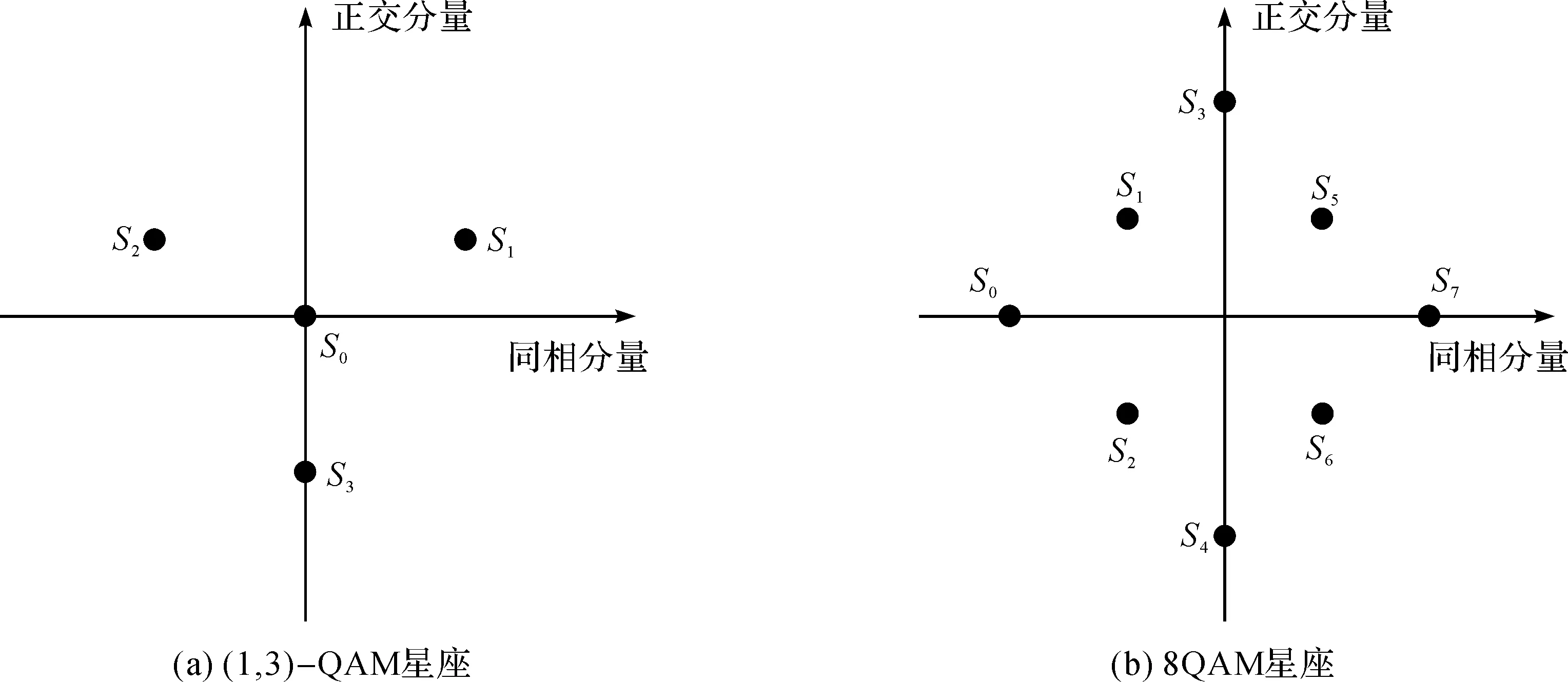
图4 (1，3)-QAM和8QAM星座Fig.4 Constellation diagram of (1,3)-QAM and 8QAM

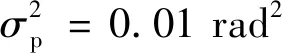
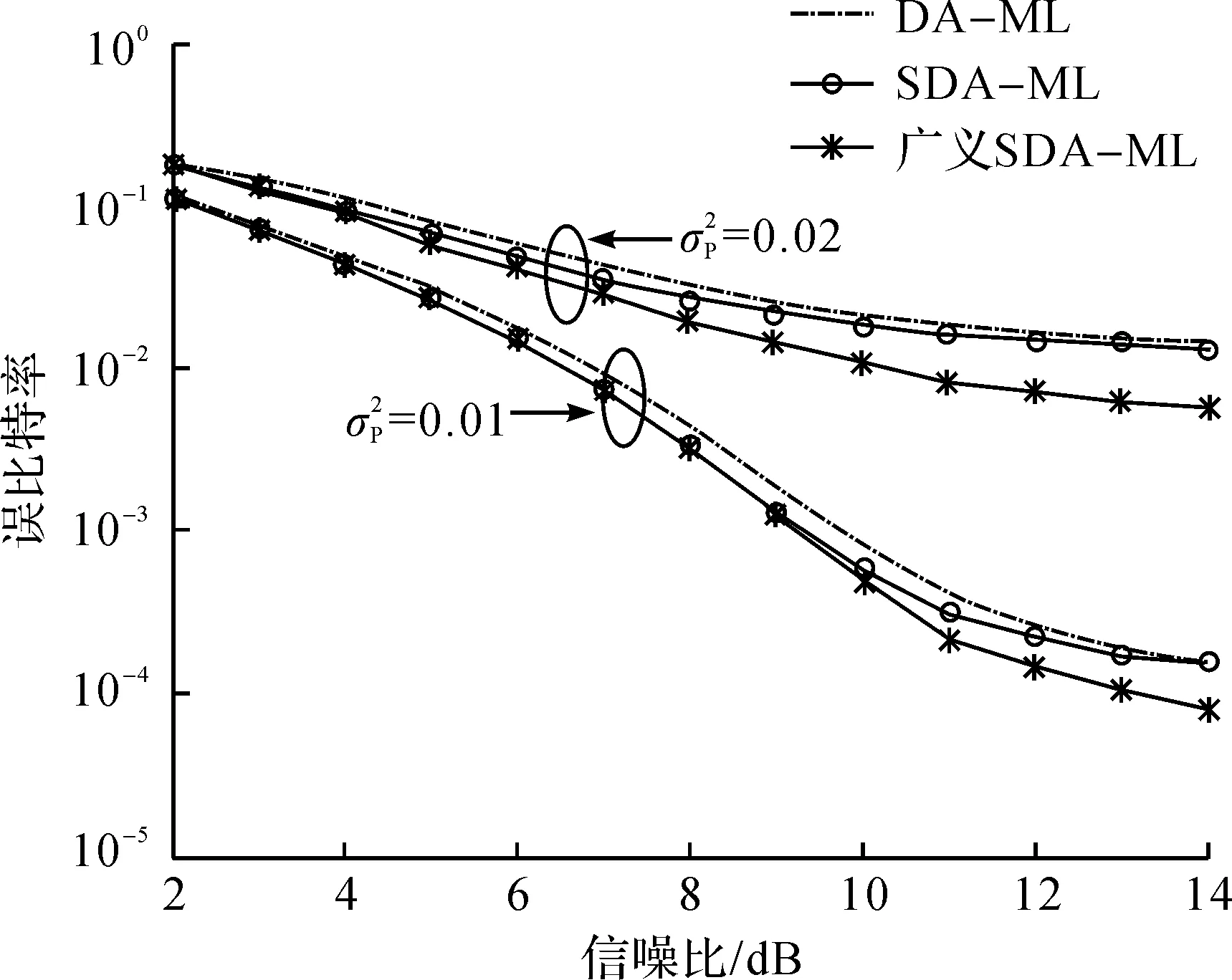
图5 (1，3)-QAM下3种相位估计算法的BEP性能比较Fig.5 BEP performance comparison of (1,3)-QAM with three phase estimation algorithms

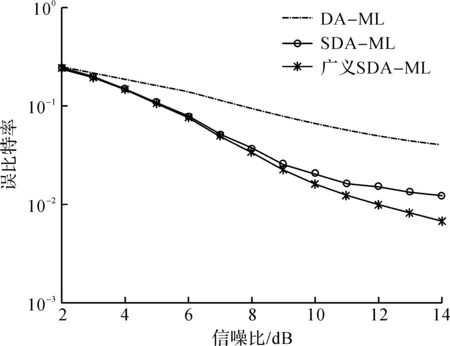
图6 8QAM下3种相位估计算法的BEP性能比较Fig.6 BEP performance comparison of 8QAM with three phase estimation algorithms

4 结 语

传统的SDA-ML载波相位估计算法考虑了软判决，具有星座无关性和低延时的特点，在此基础上本研究引入多元高斯分布模型，导出了广义SDA-ML载波相位估计算法。仿真试验结果表明，广义SDA-ML算法对相位噪声具有较强的鲁棒性。广义SDA-ML算法可以有效地降低由线性相位噪声带来的误差下限，因此，我们提出的方法具有更准确的相位估计性能。